2021-2022学年北师大版数学九年级下册1.5.三角函数的应用 课件(20张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级下册1.5.三角函数的应用 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 23:23:44 | ||
图片预览








文档简介
(共20张PPT)
1.5. 三角函数的应用
第一章 直角三角形的边角关系
温故知新
两锐角的关系:
三边的关系:.
边与角的关系:
直角三角的边角关系
c2
900
a2+b2=
∠A+∠B=
锐角三角函数
b
A
B
C
a
┌
c
sinA=cosB
cosA=sinB
tanA=
a
c
=
b
c
=
a
b
=
1
tanB
新知探究
特殊角的三角函数值:
60°
45°
30°
tanα
cosα
sinα
三角函数值
角α
三角函数
1
2
2
3
1
2
2
2
2
1
情境引入
定义:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向,旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度
方向角
北
南
西
东
东北
东南
西北
西南
45°
45°
北偏东60°
北偏西35°
南偏东30°
60°
35°
30°
南偏西45°
45°
45°
45°
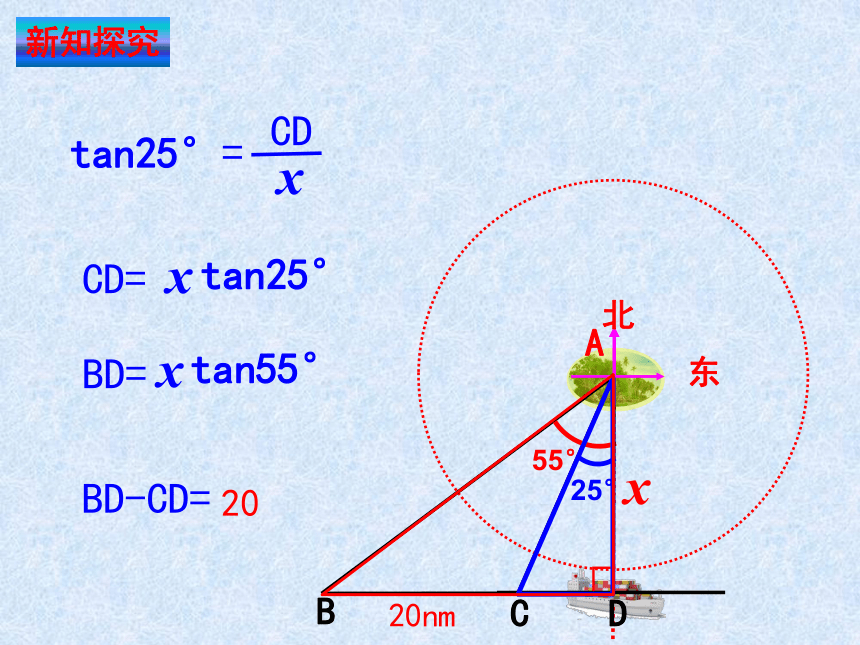
如图,海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处。之后,
货轮继续向东航行.
货轮继续航行会有
触礁的危险吗?
新知探究
A
B
D
东
北
55°
25°
C
20nm
如图,海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处。之后,
货轮继续向东航行.
货轮继续航行会有
触礁的危险吗?
新知探究
A
B
D
东
北
55°
25°
C
20nm
∟
x
CD=
tan25°=
CD
x
x
tan25°
BD=
x
tan55°
BD-CD=
20
新知探究
解:
设AD=x
则在Rt△ABD中
在Rt△ACD中,
解得:
所以,这船继续向东航行是安全的.
∵BC=BD-CD
BD=AD·tan∠BAD
CD=AD·tan∠CAD
∴BC=x·(tan55°-tan25°)
D
A
B
C
20nm
x
∟
55°
25°
x ≈20.79
>10
由点A作AD⊥BC于点D,
=x·tan55°
=x·tan25°
=20
新知归纳
(1)仔细审题,根据题意画出图形;
(2)将条件转化为几何图形中的边、角关系,把实际问题转化为解直角三角形的问题;
(3)选择合适的边角关系式,简化运算;
(4)检验答案是否符合实际意义。
利用三角函数解决实际问题的一般过程
温故知新
仰角:
俯角:
举头望明月
低头看鱼塘
α
β
新知探究
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m).
A
B
C
D
50m
30°
60°
AC-BC=
50
等量关系:
AC=
BC=
tan30°=
AC
CD
tan60°=
BC
CD
CD
tan60°
CD
tan30°
新知探究
解:
A
B
C
D
50m
30°
60°
∠ACD=90°
∠A=30°,
,AB=50m,
∠DBC=60°,
答:该塔约有43m高.
设塔高为x米
∵tanA=
AC
x
tan∠CBD=
BC
x
tan30°
∴AC=
x
BC=
tan60°
x
tan30°
x
tan60°
x
∴
-
=50
x-
2
x
=50
解得:
x=25
≈43(m)
x
新知探究
某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
40°
35°
A
B
C
D
∟
AC-AB
=CD-BD
CB
AD=
AB·
sin40°
AC=
AD
sin35°
新知探究
如图,∠ADB=90°,
40°
35°
A
B
C
∟
D
求(1)AC-AB.
AB=4m.
∠ABD=40°,
∠C=35°,
∵sin40°
AB
AD
=
∴AD=
AB·
sin40°
∵sin35°
AC
AD
=
∴AC=
AD
sin35°
=
AB·
sin40°
sin35°
=
4×
0.643
0.574
≈4.48
(m)
答:调整后的楼梯会加长约0.48m.
AC-AB=
4.48-4
≈0.48
(m)
新知探究
如图,∠ADB=90°,
40°
35°
A
B
C
∟
D
求CB
AB=4m.
∠ABD=40°,
∠C=35°,
(AD=
sin40°)
AB
∵tan40°
BD
AD
=
tan40°
∴BD=
AD
∵tan35°
CD
AD
=
tan35°
∴CD=
AD
∴CB=
CD-BD
tan35°
=
AD
tan40°
-
AD
tan35°
1
tan40°
-
1
=AD(
)
=4×
0.643(
0.700
1
0.839
-
1
)
≈0.61
(m)
答:楼梯多占约0.61m长的一段地面.
练一练
1.如图,AB是斜靠在墙上的长梯,D是梯上一点,梯脚B与墙脚的距离为1.6 m(即BC的长),点D与墙的距离为1.4 m(即DE的长),BD长为0.55 m,则梯子的长为( )
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
B
练一练
2.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
C
练一练
3.如图,AB是伸缩式遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长是________米.(假设夏至的正午时刻阳光与地平面的夹角为60°)
练一练
4.如图,已知电线杆AB直立于地面上,它的影子恰好照在土坡的坡面CD和地面BC上,如果CD与地面成45°,∠A=60°,CD=4 m,BC=(4 -2 )m,则电线杆AB的长为________.
6
课堂小结
(1)仔细审题,根据题意画出图形;
(2)将条件转化为几何图形中的边、角关系,把实际问题转化为解直角三角形的问题;
(3)选择合适的边角关系式,简化运算;
(4)检验答案是否符合实际意义。
利用三角函数解决实际问题的一般过程
作业
P21
1,2,3,4
1.5. 三角函数的应用
第一章 直角三角形的边角关系
温故知新
两锐角的关系:
三边的关系:.
边与角的关系:
直角三角的边角关系
c2
900
a2+b2=
∠A+∠B=
锐角三角函数
b
A
B
C
a
┌
c
sinA=cosB
cosA=sinB
tanA=
a
c
=
b
c
=
a
b
=
1
tanB
新知探究
特殊角的三角函数值:
60°
45°
30°
tanα
cosα
sinα
三角函数值
角α
三角函数
1
2
2
3
1
2
2
2
2
1
情境引入
定义:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向,旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度
方向角
北
南
西
东
东北
东南
西北
西南
45°
45°
北偏东60°
北偏西35°
南偏东30°
60°
35°
30°
南偏西45°
45°
45°
45°
如图,海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处。之后,
货轮继续向东航行.
货轮继续航行会有
触礁的危险吗?
新知探究
A
B
D
东
北
55°
25°
C
20nm
如图,海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处。之后,
货轮继续向东航行.
货轮继续航行会有
触礁的危险吗?
新知探究
A
B
D
东
北
55°
25°
C
20nm
∟
x
CD=
tan25°=
CD
x
x
tan25°
BD=
x
tan55°
BD-CD=
20
新知探究
解:
设AD=x
则在Rt△ABD中
在Rt△ACD中,
解得:
所以,这船继续向东航行是安全的.
∵BC=BD-CD
BD=AD·tan∠BAD
CD=AD·tan∠CAD
∴BC=x·(tan55°-tan25°)
D
A
B
C
20nm
x
∟
55°
25°
x ≈20.79
>10
由点A作AD⊥BC于点D,
=x·tan55°
=x·tan25°
=20
新知归纳
(1)仔细审题,根据题意画出图形;
(2)将条件转化为几何图形中的边、角关系,把实际问题转化为解直角三角形的问题;
(3)选择合适的边角关系式,简化运算;
(4)检验答案是否符合实际意义。
利用三角函数解决实际问题的一般过程
温故知新
仰角:
俯角:
举头望明月
低头看鱼塘
α
β
新知探究
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m).
A
B
C
D
50m
30°
60°
AC-BC=
50
等量关系:
AC=
BC=
tan30°=
AC
CD
tan60°=
BC
CD
CD
tan60°
CD
tan30°
新知探究
解:
A
B
C
D
50m
30°
60°
∠ACD=90°
∠A=30°,
,AB=50m,
∠DBC=60°,
答:该塔约有43m高.
设塔高为x米
∵tanA=
AC
x
tan∠CBD=
BC
x
tan30°
∴AC=
x
BC=
tan60°
x
tan30°
x
tan60°
x
∴
-
=50
x-
2
x
=50
解得:
x=25
≈43(m)
x
新知探究
某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
40°
35°
A
B
C
D
∟
AC-AB
=CD-BD
CB
AD=
AB·
sin40°
AC=
AD
sin35°
新知探究
如图,∠ADB=90°,
40°
35°
A
B
C
∟
D
求(1)AC-AB.
AB=4m.
∠ABD=40°,
∠C=35°,
∵sin40°
AB
AD
=
∴AD=
AB·
sin40°
∵sin35°
AC
AD
=
∴AC=
AD
sin35°
=
AB·
sin40°
sin35°
=
4×
0.643
0.574
≈4.48
(m)
答:调整后的楼梯会加长约0.48m.
AC-AB=
4.48-4
≈0.48
(m)
新知探究
如图,∠ADB=90°,
40°
35°
A
B
C
∟
D
求CB
AB=4m.
∠ABD=40°,
∠C=35°,
(AD=
sin40°)
AB
∵tan40°
BD
AD
=
tan40°
∴BD=
AD
∵tan35°
CD
AD
=
tan35°
∴CD=
AD
∴CB=
CD-BD
tan35°
=
AD
tan40°
-
AD
tan35°
1
tan40°
-
1
=AD(
)
=4×
0.643(
0.700
1
0.839
-
1
)
≈0.61
(m)
答:楼梯多占约0.61m长的一段地面.
练一练
1.如图,AB是斜靠在墙上的长梯,D是梯上一点,梯脚B与墙脚的距离为1.6 m(即BC的长),点D与墙的距离为1.4 m(即DE的长),BD长为0.55 m,则梯子的长为( )
A.4.50 m
B.4.40 m
C.4.00 m
D.3.85 m
B
练一练
2.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
A.5sin 36°米
B.5cos 36°米
C.5tan 36°米
D.10tan 36°米
C
练一练
3.如图,AB是伸缩式遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长是________米.(假设夏至的正午时刻阳光与地平面的夹角为60°)
练一练
4.如图,已知电线杆AB直立于地面上,它的影子恰好照在土坡的坡面CD和地面BC上,如果CD与地面成45°,∠A=60°,CD=4 m,BC=(4 -2 )m,则电线杆AB的长为________.
6
课堂小结
(1)仔细审题,根据题意画出图形;
(2)将条件转化为几何图形中的边、角关系,把实际问题转化为解直角三角形的问题;
(3)选择合适的边角关系式,简化运算;
(4)检验答案是否符合实际意义。
利用三角函数解决实际问题的一般过程
作业
P21
1,2,3,4
