2021-2022学年华东师大版八年级数学上册14.1 勾股定理 课件(1)(共24张ppt)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册14.1 勾股定理 课件(1)(共24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 16:32:48 | ||
图片预览







文档简介
(共24张PPT)
14.1 勾股定理(1)
华师大版 八年级数学(上册)
——数形结合之美
你想知道吗
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?~
探索勾股定理
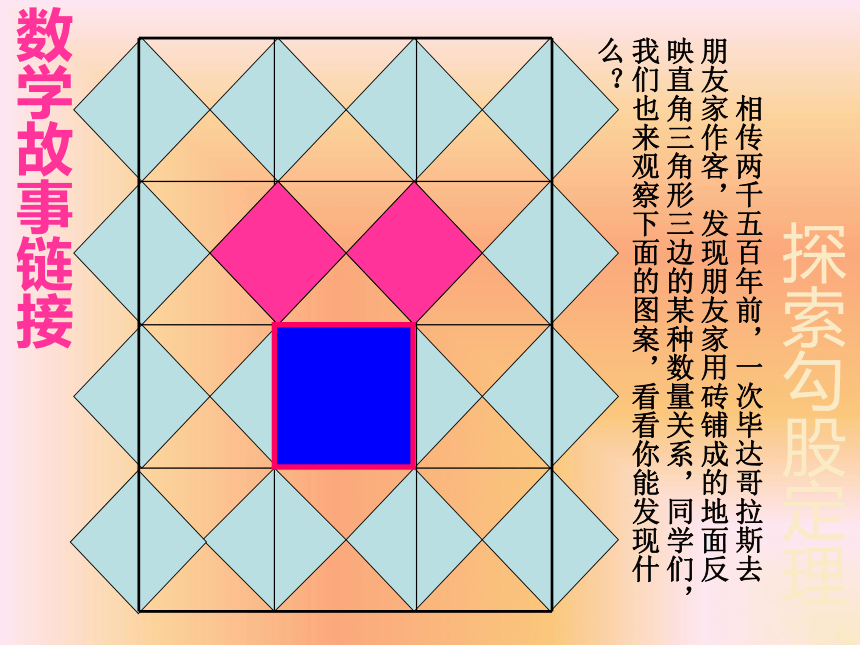
数学故事链接
相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
探索勾股定理
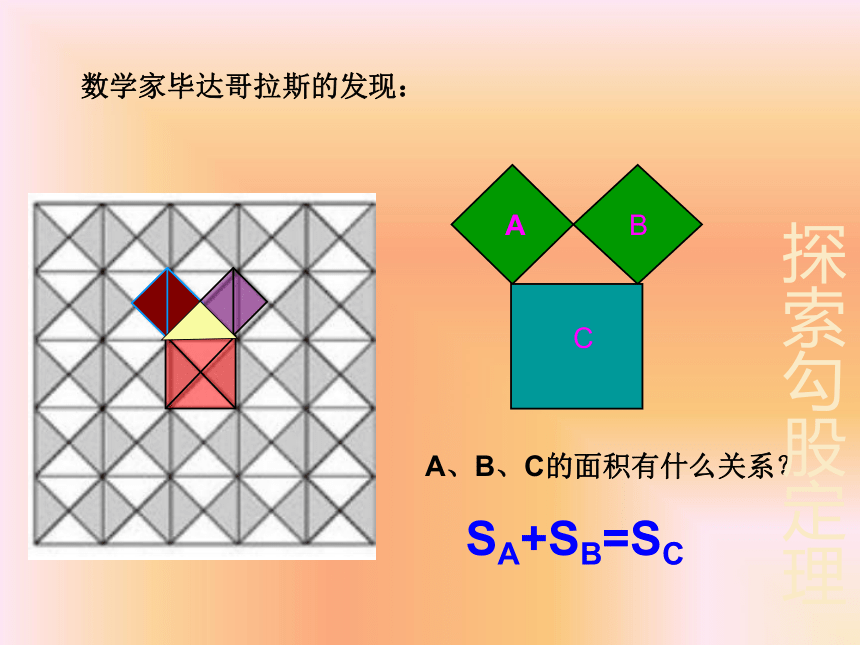
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
SA+SB=SC
A
B
C
探索勾股定理
A
B
C
A
B
C
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-1
图1-2
9
16
25
16
36
52
探索勾股定理
A
B
C
SA=a2
SB=b2
SC=c2
a
b
c
a2+b2=c2
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
SA+SB=SC
探索勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么c2=a2+b2.
猜想
a
b
c
勾
股
弦
探索勾股定理
b
a
c
s2
s1
试一试
请利用此图象,证明勾股定理:
a2+b2=c2
探索勾股定理
走进数学史
勾股定理的由来
这个定理在中国又称为“商高定理”,在外国称为“毕达哥拉
斯定理”。为什么一个定理有这么多名称呢?商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。
在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。“什么是”勾、股“呢?在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。由于勾股定理的内容最早见于商高的话中,所以人们就把这个定理叫作"商高定理"。
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。希腊另一位数学家欧几
里德(Euclid,是公元前三百年左右的人)在编著《几何原本》
时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个
定理称为“毕达哥拉斯定理”,以后就流传开了。(为了庆祝这一定理的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做“百牛定理”.)
走进数学史
勾股定理的证明方法
证法一
证法二
证法三
(邹元治证明)
(赵爽证明) 赵爽:我国古代数学家
走进数学史
勾股定理的证明方法
证法四
证法五
证法六
(加菲尔德证明) 加菲尔德:第二十任总统
(梅文鼎证明) 梅文鼎:清代天文、数学家
(项明达证明) 项明达:清代数学家
走进数学史
勾股定理的证明
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
现在在网络上看到较多的是16种,包括前面的6种,还有:
欧几里得证明、 利用相似三角形性质证明、
杨作玫证明、 李锐证明、
利用切割线定理证明、 利用多列米定理证明、
作直角三角形的内切圆证明、利用反证法证明、
辛卜松证明、 陈杰证明。
走进数学史
应用勾股定理
a
b
c
确定斜边
c2= a2+b2
?
a
c
b
确定斜边
b2= a2+c2
?
b
c
a
确定斜边
a2= b2+c2
?
应用勾股定理
c2=a2 +b2
a
b
c
b2= c2 - a2
a2= c2 - b2
灵活运用
{
应用勾股定理
已知△ABC的三边分别是a,b,c,
若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
A
B
C
选一选
应用勾股定理
讲一讲
8
6
A
B
C
求图中直角三角形的未知边的长度。
15
17
A
B
C
勾股定理,想得再多一点
(1)若a=5,b=12, 则c =___________.
在Rt△ABC中,
(2)若c=4,b= 2 ,则a =______.
∠C=900 .
做一做
勾股定理,想得再多一点
如图,受台风莫拉克影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
勾股定理,想得再多一点
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?~
回头再看看
说说这节课你有什么收获?
内容总结:
(1)运用勾股定理的条件是什么?
(2)勾股定理揭示了直角三角形的什么关系?
(3)勾股定理有什么用途?
方法总结:
用直角三角形三边表示三个正方形面积——观察归纳发现勾股定理——任意画一个直角三角形,再验证自己的发现。
课堂之外还需要巩固提高
家庭作业:
课本P55 习题2
补充:
1、求下列直角三角形中未知边的长:
补充:
1、求下列直角三角形中未知边的长:
2、如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,
树顶落在离树根24米处.大树在折断之前高多少?
再见
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
14.1 勾股定理(1)
华师大版 八年级数学(上册)
——数形结合之美
你想知道吗
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?~
探索勾股定理
数学故事链接
相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
探索勾股定理
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
SA+SB=SC
A
B
C
探索勾股定理
A
B
C
A
B
C
A的面积(单位面积)
B的面积(单位面积)
C的面积(单位面积)
图1-1
图1-2
9
16
25
16
36
52
探索勾股定理
A
B
C
SA=a2
SB=b2
SC=c2
a
b
c
a2+b2=c2
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
SA+SB=SC
探索勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么c2=a2+b2.
猜想
a
b
c
勾
股
弦
探索勾股定理
b
a
c
s2
s1
试一试
请利用此图象,证明勾股定理:
a2+b2=c2
探索勾股定理
走进数学史
勾股定理的由来
这个定理在中国又称为“商高定理”,在外国称为“毕达哥拉
斯定理”。为什么一个定理有这么多名称呢?商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。
在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。“什么是”勾、股“呢?在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。由于勾股定理的内容最早见于商高的话中,所以人们就把这个定理叫作"商高定理"。
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。希腊另一位数学家欧几
里德(Euclid,是公元前三百年左右的人)在编著《几何原本》
时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个
定理称为“毕达哥拉斯定理”,以后就流传开了。(为了庆祝这一定理的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做“百牛定理”.)
走进数学史
勾股定理的证明方法
证法一
证法二
证法三
(邹元治证明)
(赵爽证明) 赵爽:我国古代数学家
走进数学史
勾股定理的证明方法
证法四
证法五
证法六
(加菲尔德证明) 加菲尔德:第二十任总统
(梅文鼎证明) 梅文鼎:清代天文、数学家
(项明达证明) 项明达:清代数学家
走进数学史
勾股定理的证明
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
现在在网络上看到较多的是16种,包括前面的6种,还有:
欧几里得证明、 利用相似三角形性质证明、
杨作玫证明、 李锐证明、
利用切割线定理证明、 利用多列米定理证明、
作直角三角形的内切圆证明、利用反证法证明、
辛卜松证明、 陈杰证明。
走进数学史
应用勾股定理
a
b
c
确定斜边
c2= a2+b2
?
a
c
b
确定斜边
b2= a2+c2
?
b
c
a
确定斜边
a2= b2+c2
?
应用勾股定理
c2=a2 +b2
a
b
c
b2= c2 - a2
a2= c2 - b2
灵活运用
{
应用勾股定理
已知△ABC的三边分别是a,b,c,
若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
A
B
C
选一选
应用勾股定理
讲一讲
8
6
A
B
C
求图中直角三角形的未知边的长度。
15
17
A
B
C
勾股定理,想得再多一点
(1)若a=5,b=12, 则c =___________.
在Rt△ABC中,
(2)若c=4,b= 2 ,则a =______.
∠C=900 .
做一做
勾股定理,想得再多一点
如图,受台风莫拉克影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
勾股定理,想得再多一点
国庆节前,为了更好观看阅兵式,小明妈妈买了一部42英寸(106厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有85厘米长和64厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?~
回头再看看
说说这节课你有什么收获?
内容总结:
(1)运用勾股定理的条件是什么?
(2)勾股定理揭示了直角三角形的什么关系?
(3)勾股定理有什么用途?
方法总结:
用直角三角形三边表示三个正方形面积——观察归纳发现勾股定理——任意画一个直角三角形,再验证自己的发现。
课堂之外还需要巩固提高
家庭作业:
课本P55 习题2
补充:
1、求下列直角三角形中未知边的长:
补充:
1、求下列直角三角形中未知边的长:
2、如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,
树顶落在离树根24米处.大树在折断之前高多少?
再见
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
