19.1变量与函数复习课 课件(共18张PPT)
文档属性
| 名称 | 19.1变量与函数复习课 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 08:35:26 | ||
图片预览






文档简介
(共18张PPT)
19.1变量与函数 复习课
人教版 八年级下册
1.了解变量与常量的意义.会区分常量与变量,能够建立变量之间的关系式.
2.明确函数的相关概念,会求函数值和自变量的取值范围.
3.掌握画函数图象的一般步骤;了解函数的三种表示方法及其优点;能通过函数图象说出变量的变化情况,并对函数关系进行分析.
学习目标
知识梳理1
2.函数
概念:在一个变化过程中,如果有两个变量 与 ,并且对于 的每一个确定的值, 都有唯一确定的值与其对应,那么我们就说 是自变量, 是 的函数.
函数值:如果当 时 ,那么 叫做当自变量的值为 时的函数值.
自变量的取值范围:既要使函数解析式有意义,又要符合实际意义.
1.常量与变量: 数值发生变化的量叫变量 ,
数值始终不变的量叫常量.
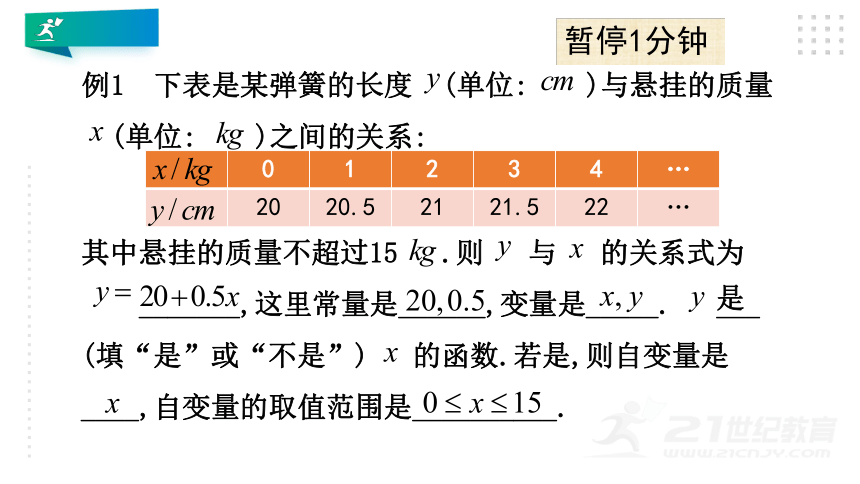
其中悬挂的质量不超过15 .则 与 的关系式为
_______,这里常量是______,变量是_____. ___
(填“是”或“不是”) 的函数.若是,则自变量是
____,自变量的取值范围是__________.
暂停1分钟
例1 下表是某弹簧的长度 (单位: )与悬挂的质量
(单位: )之间的关系:
0 1 2 3 4 …
20 20.5 21 21.5 22 …
是
例2 (1)等腰三角形的周长为20,腰长为 ,底边长为 , 求 与 之间的函数解析式及自变量的取值范围.
解得自变量的取值范围是 .
解:根据题意,得 与 之间的函数解析式为 ,
自变量 应满足的条件为 ,
暂停2分钟
解:根据题意得
解得 且 且 .
方法总结:(1)二次根式中被开方数大于等于0.
(2)分式中分母不为0.
(3)零指数幂底数不为0.
(4)实际意义.
例2 (2)函数 中,自变量 的取值范围是______________________.
且
且
暂停1分钟
函数图象的画法
列表:表中给出一些自变量的值及其对应的函数值
描点:在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点
连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来
注意:实际问题的函数图象还要考虑问题的实际意义
知识梳理2
例3:(1)如果点(2,4)在函数 的图象上,则 的值为( )
A.-1 B.1 C.2 D.3
C
(2)下列各点中,在函数 图象上的是( )
A.(2,3) B.(3,6) C.(-2.5,-4) D.(-1,1)
C
提示:点的横、纵坐标分别
为x、y的取值。
暂停1分钟
例4:小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地.下列函数图象能表达这一过程的是( )
C
利用函数的图象解决实际问题时,正确理解函数图象横、纵坐标表示的意义,从图象中获得信息。
数形结合是数学中解决实际问题的重要方法。
暂停2分钟
函数的表示方法
解析式法:准确地反映函数与自变量之间的数量关系
列表法:具体地反映函数与自变量之间的数值对应关系
图象法:直观地反映函数随自变量的变化而变化的规律
知识梳理3
例5.小亮因感冒发烧住院治疗,护士为了较直观地反映小亮某天24小时的体温与时间的关系,比较好的方式应该选择( )
A.列表法 B.图象法
C.函数解析法 D.以上三种方法都可以
B
暂停1分钟
1.汽车以每小时60千米的速度匀速行驶,行驶路程为 千米,行驶的时间为 小时,则 与 的函数解析式为___________.
2.现有200本笔记本分给学生,每人5本,余下的本数 和学生数 之间的函数解析式为_______________,自变量 的取值范围是_____________.
3.根据下表写出的函数解析式为( )
x 0 5 10 15
y 3 3.5 4 4.5
D
针对性训练
A. B. C. D.
暂停2分钟
4.同一温度的华氏温度 ( )与摄氏温度 ( )之间的函数关系是
,如果某一温度的摄氏温度为25 ,那么它的华氏温度是____ .
5.若函数 则当函数值 时,自变量 的值是( )
A. B. C. 或 D. 或
77
D
暂停1分钟
6.如图是某地区一天的气温随时间变化的图象,根据图象回答在这一天中:
(1)气温 (℃)____(填“是”或“不是”)时间 (时)的函数;
(2)____时气温最高,____时气温最低;
(3)10时气温是____℃;____________时气温是4℃;
(4)_________________________时间内,气温不断上升;
(5)______________________时间内,气温持续不变.
是
16
2
5
9时,22
2时至12时,14时至16时
12时至14时
暂停2分钟
7.一盘蚊香长100 cm,点燃时每小时缩短10 cm,小明在蚊香点燃5 h后将它熄灭,过了2 h,他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度 (cm)与所经过时间 (h)之间的函数关系的是 ( )
C
暂停1分钟
如图的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟.
其中正确的说法是_________.(把你认为正确说法的序号都填上)
①③
能力提升
暂停2分钟
1.常量与变量: 数值发生变化的量叫变量 ,数值始终不变的量叫常量.
2.函数的定义:在一个变化过程中,如果有两个变量 与 ,并且对于 的每一个确定的值, 都有唯一确定的值与其对应,那么我们就说 是自变 量, 是 的函数.
3.描点法画图象的步骤: 列表、描点、连线.
4.函数的三种表示方法: 解析式法、列表法、图象法.
5.数学思想:数形结合.
课堂小结
必做题:习题19.1 第5-7题
选做题:习题19.1 第14、15题
课后作业
19.1变量与函数 复习课
人教版 八年级下册
1.了解变量与常量的意义.会区分常量与变量,能够建立变量之间的关系式.
2.明确函数的相关概念,会求函数值和自变量的取值范围.
3.掌握画函数图象的一般步骤;了解函数的三种表示方法及其优点;能通过函数图象说出变量的变化情况,并对函数关系进行分析.
学习目标
知识梳理1
2.函数
概念:在一个变化过程中,如果有两个变量 与 ,并且对于 的每一个确定的值, 都有唯一确定的值与其对应,那么我们就说 是自变量, 是 的函数.
函数值:如果当 时 ,那么 叫做当自变量的值为 时的函数值.
自变量的取值范围:既要使函数解析式有意义,又要符合实际意义.
1.常量与变量: 数值发生变化的量叫变量 ,
数值始终不变的量叫常量.
其中悬挂的质量不超过15 .则 与 的关系式为
_______,这里常量是______,变量是_____. ___
(填“是”或“不是”) 的函数.若是,则自变量是
____,自变量的取值范围是__________.
暂停1分钟
例1 下表是某弹簧的长度 (单位: )与悬挂的质量
(单位: )之间的关系:
0 1 2 3 4 …
20 20.5 21 21.5 22 …
是
例2 (1)等腰三角形的周长为20,腰长为 ,底边长为 , 求 与 之间的函数解析式及自变量的取值范围.
解得自变量的取值范围是 .
解:根据题意,得 与 之间的函数解析式为 ,
自变量 应满足的条件为 ,
暂停2分钟
解:根据题意得
解得 且 且 .
方法总结:(1)二次根式中被开方数大于等于0.
(2)分式中分母不为0.
(3)零指数幂底数不为0.
(4)实际意义.
例2 (2)函数 中,自变量 的取值范围是______________________.
且
且
暂停1分钟
函数图象的画法
列表:表中给出一些自变量的值及其对应的函数值
描点:在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点
连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来
注意:实际问题的函数图象还要考虑问题的实际意义
知识梳理2
例3:(1)如果点(2,4)在函数 的图象上,则 的值为( )
A.-1 B.1 C.2 D.3
C
(2)下列各点中,在函数 图象上的是( )
A.(2,3) B.(3,6) C.(-2.5,-4) D.(-1,1)
C
提示:点的横、纵坐标分别
为x、y的取值。
暂停1分钟
例4:小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地.下列函数图象能表达这一过程的是( )
C
利用函数的图象解决实际问题时,正确理解函数图象横、纵坐标表示的意义,从图象中获得信息。
数形结合是数学中解决实际问题的重要方法。
暂停2分钟
函数的表示方法
解析式法:准确地反映函数与自变量之间的数量关系
列表法:具体地反映函数与自变量之间的数值对应关系
图象法:直观地反映函数随自变量的变化而变化的规律
知识梳理3
例5.小亮因感冒发烧住院治疗,护士为了较直观地反映小亮某天24小时的体温与时间的关系,比较好的方式应该选择( )
A.列表法 B.图象法
C.函数解析法 D.以上三种方法都可以
B
暂停1分钟
1.汽车以每小时60千米的速度匀速行驶,行驶路程为 千米,行驶的时间为 小时,则 与 的函数解析式为___________.
2.现有200本笔记本分给学生,每人5本,余下的本数 和学生数 之间的函数解析式为_______________,自变量 的取值范围是_____________.
3.根据下表写出的函数解析式为( )
x 0 5 10 15
y 3 3.5 4 4.5
D
针对性训练
A. B. C. D.
暂停2分钟
4.同一温度的华氏温度 ( )与摄氏温度 ( )之间的函数关系是
,如果某一温度的摄氏温度为25 ,那么它的华氏温度是____ .
5.若函数 则当函数值 时,自变量 的值是( )
A. B. C. 或 D. 或
77
D
暂停1分钟
6.如图是某地区一天的气温随时间变化的图象,根据图象回答在这一天中:
(1)气温 (℃)____(填“是”或“不是”)时间 (时)的函数;
(2)____时气温最高,____时气温最低;
(3)10时气温是____℃;____________时气温是4℃;
(4)_________________________时间内,气温不断上升;
(5)______________________时间内,气温持续不变.
是
16
2
5
9时,22
2时至12时,14时至16时
12时至14时
暂停2分钟
7.一盘蚊香长100 cm,点燃时每小时缩短10 cm,小明在蚊香点燃5 h后将它熄灭,过了2 h,他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度 (cm)与所经过时间 (h)之间的函数关系的是 ( )
C
暂停1分钟
如图的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟.
其中正确的说法是_________.(把你认为正确说法的序号都填上)
①③
能力提升
暂停2分钟
1.常量与变量: 数值发生变化的量叫变量 ,数值始终不变的量叫常量.
2.函数的定义:在一个变化过程中,如果有两个变量 与 ,并且对于 的每一个确定的值, 都有唯一确定的值与其对应,那么我们就说 是自变 量, 是 的函数.
3.描点法画图象的步骤: 列表、描点、连线.
4.函数的三种表示方法: 解析式法、列表法、图象法.
5.数学思想:数形结合.
课堂小结
必做题:习题19.1 第5-7题
选做题:习题19.1 第14、15题
课后作业
