第一单元 圆柱与圆锥 测试卷-2021-2022学年北师版数学六年级下册(含答案)
文档属性
| 名称 | 第一单元 圆柱与圆锥 测试卷-2021-2022学年北师版数学六年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 283.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 16:17:55 | ||
图片预览


文档简介
单元达标测试卷
第一单元 圆柱与圆锥
一、认真审题,填一填。(第1小题4分,其余每小题2分,共22分)
1.6.56 m2=( )dm2 3 dm2 22 cm2=( )dm2
8 L 50 mL=( )L 5 m3 25 dm3=( )m3=( )L
2.一个圆锥的体积是18.84 dm3,底面积是9.42 dm2,高是( )dm。
3.一个圆柱体,它的底面半径是2厘米,高是5厘米,将它沿底面半径分成若干等份,然后拼成一个近似的长方体,这个长方体的底面积是( )平方厘米,高是( )厘米。
4.如图,一个底面直径为20 cm,长为50 cm的圆柱形通风管,沿着地面滚动一周,滚过的面积是( )cm2。
5.一个近似于圆锥形状的野营帐篷(如图所示),它的底面半径是3米,高是2.4米。帐篷的占地面积是( )平方米,它的体积是( )。
6.用一块长28.26厘米、宽15.7厘米的长方形铁皮,应配上直径为( )厘米的圆形铁皮,可以做成一个容积最大的容器。
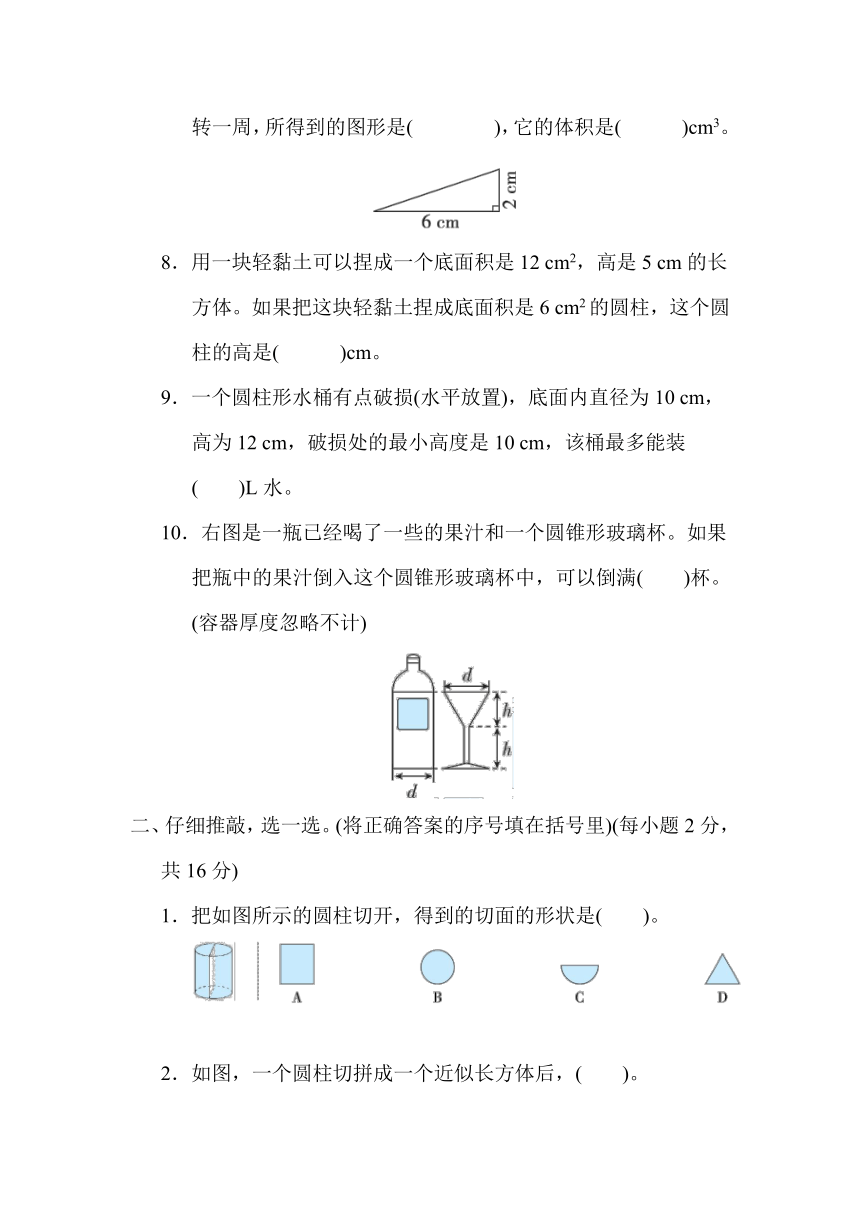
7.如图是一个直角三角形,以6 cm长的直角边所在直线为轴旋转一周,所得到的图形是( ),它的体积是( )cm3。
8.用一块轻黏土可以捏成一个底面积是12 cm2,高是5 cm的长方体。如果把这块轻黏土捏成底面积是6 cm2的圆柱,这个圆柱的高是( )cm。
9.一个圆柱形水桶有点破损(水平放置),底面内直径为10 cm,高为12 cm,破损处的最小高度是10 cm,该桶最多能装
( )L水。
10.右图是一瓶已经喝了一些的果汁和一个圆锥形玻璃杯。如果把瓶中的果汁倒入这个圆锥形玻璃杯中,可以倒满( )杯。(容器厚度忽略不计)
二、仔细推敲,选一选。(将正确答案的序号填在括号里)(每小题2分,共16分)
1.把如图所示的圆柱切开,得到的切面的形状是( )。
2.如图,一个圆柱切拼成一个近似长方体后,( )。
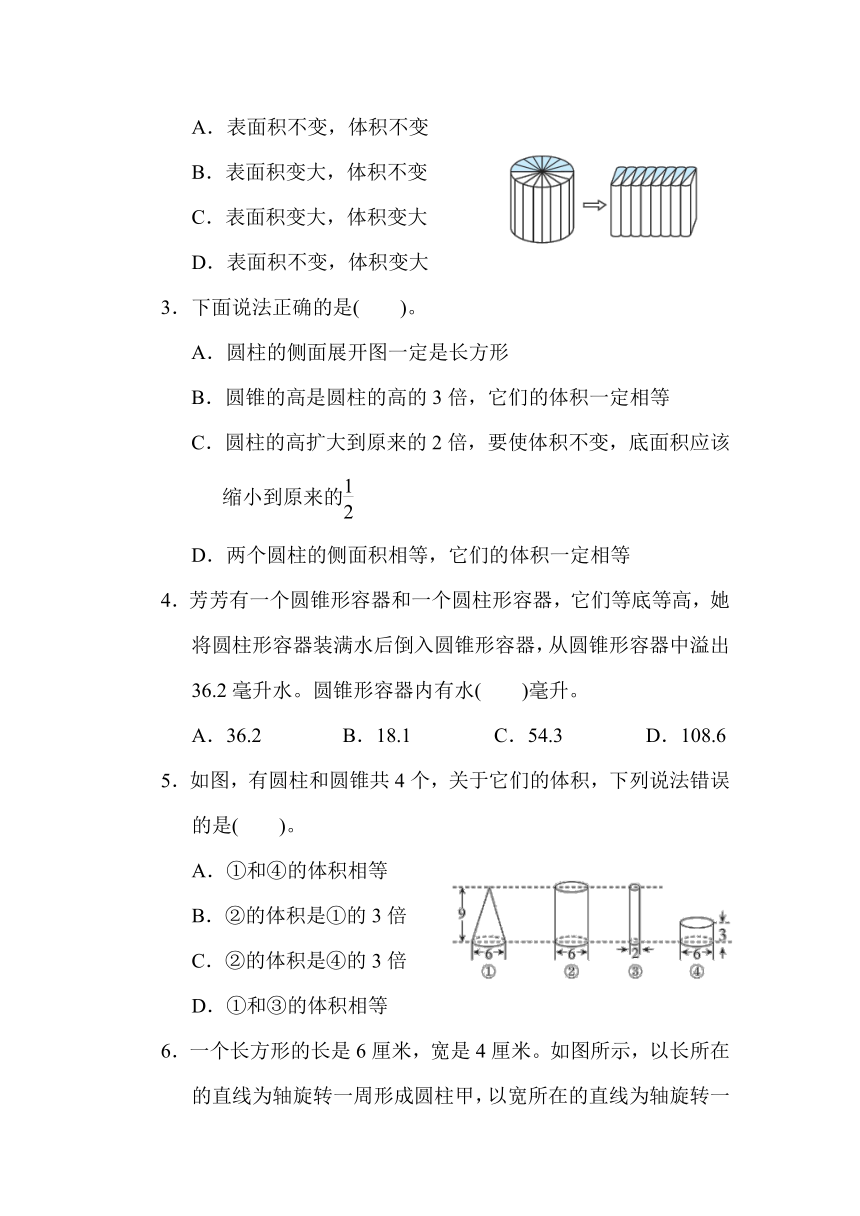
A.表面积不变,体积不变
B.表面积变大,体积不变
C.表面积变大,体积变大
D.表面积不变,体积变大
3.下面说法正确的是( )。
A.圆柱的侧面展开图一定是长方形
B.圆锥的高是圆柱的高的3倍,它们的体积一定相等
C.圆柱的高扩大到原来的2倍,要使体积不变,底面积应该缩小到原来的
D.两个圆柱的侧面积相等,它们的体积一定相等
4.芳芳有一个圆锥形容器和一个圆柱形容器,它们等底等高,她将圆柱形容器装满水后倒入圆锥形容器,从圆锥形容器中溢出36.2毫升水。圆锥形容器内有水( )毫升。
A.36.2 B.18.1 C.54.3 D.108.6
5.如图,有圆柱和圆锥共4个,关于它们的体积,下列说法错误的是( )。
A.①和④的体积相等
B.②的体积是①的3倍
C.②的体积是④的3倍
D.①和③的体积相等
6.一个长方形的长是6厘米,宽是4厘米。如图所示,以长所在的直线为轴旋转一周形成圆柱甲,以宽所在的直线为轴旋转一周形成圆柱乙。下列说法中正确的是( )。
①圆柱甲的底面积比圆柱乙的底面积大。
②圆柱甲的侧面积和圆柱乙的侧面积相等。
③圆柱甲的表面积与圆柱乙的表面积相等。
④圆柱甲的体积比圆柱乙的体积小。
A.①③ B.②④ C.①② D.③④
7.一个长方体包装盒的长是32厘米,宽是2厘米,高是1厘米。圆柱形零件的底面直径是2厘米,高是1厘米。这个包装盒内最多能放( )个零件。
A.32 B.25 C.16 D. 8
8.沙漏又称沙钟,是我国古代一种计量时间的仪器,它是根据流沙从一个容器漏到另一个容器的时间来计时的,右图是一个沙漏(由两个完全相同的圆锥组成)的示意图(单位:cm),这个沙漏的容积是( )cm3。
A.251.2 B.502.4 C.753.6
三、细心的你,算一算。(共16分)
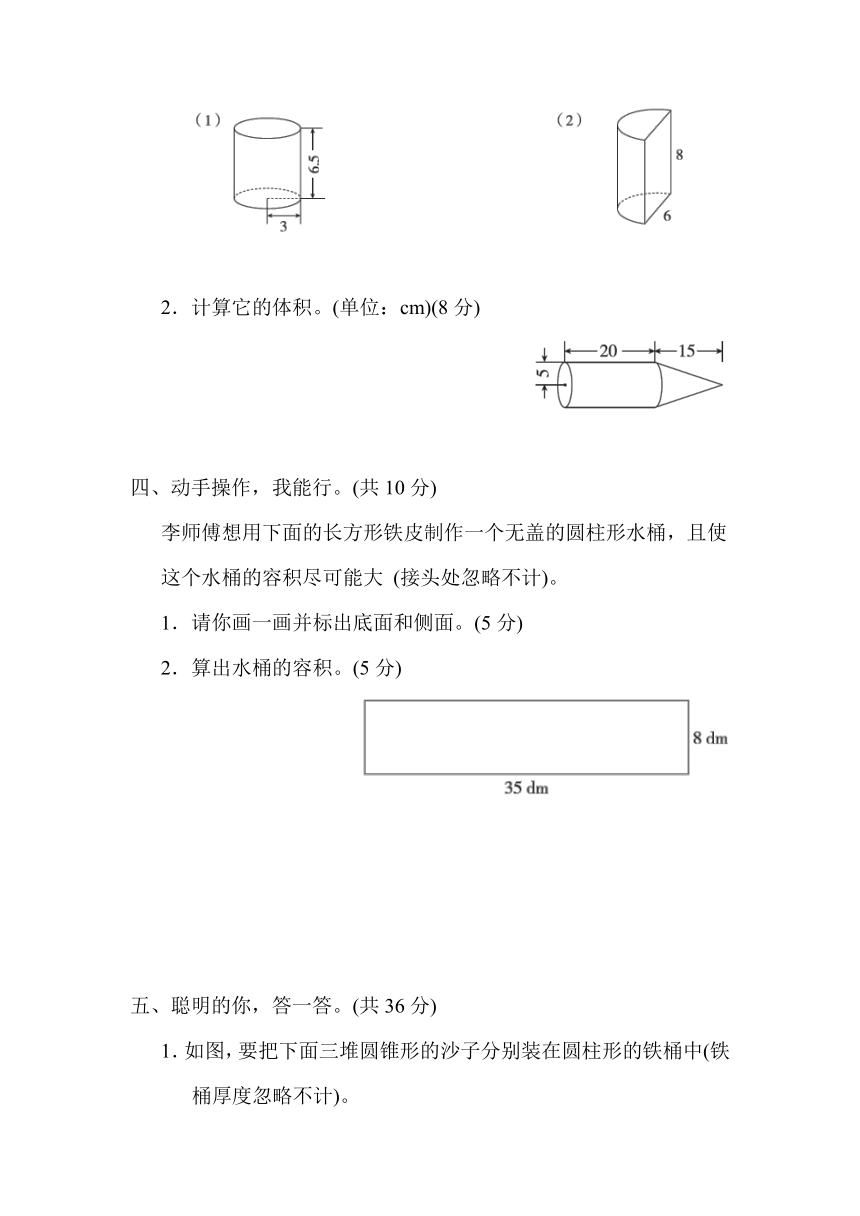
1.计算它们的表面积。(单位:cm)(8分)
2.计算它的体积。(单位:cm)(8分)
四、动手操作,我能行。(共10分)
李师傅想用下面的长方形铁皮制作一个无盖的圆柱形水桶,且使这个水桶的容积尽可能大 (接头处忽略不计)。
1.请你画一画并标出底面和侧面。(5分)
2.算出水桶的容积。(5分)
五、聪明的你,答一答。(共36分)
1.如图,要把下面三堆圆锥形的沙子分别装在圆柱形的铁桶中(铁桶厚度忽略不计)。
下面是三名同学经过测量后得到的结论。
淘气说:“第一堆沙子和铁桶等底等高,能装下。”
奇思说:“第二堆沙子和铁桶等底,高是铁桶的2倍,能装下。”
妙想说:“第三堆沙子和铁桶等高,底面直径是铁桶的2倍,能装下。”
你认为谁的说法正确?谁的说法错误?请说明理由。(5分)
2.圆柱形的核桃露罐的底面直径是5 cm,高是13 cm。将24罐这种核桃露放在长方体箱子里,每排放8罐,放3排,刚好合适。这个箱子内部的长、宽、高分别是多少厘米?这个箱子的容积是多少?(6分)
3.把一块棱长10厘米的正方体铁块熔铸成一块底面直径是20厘米的圆锥形铁块。这块圆锥形铁块的高约是多少?
解答这道题时,乐乐列出了下面的综合算式:
10×10×10÷[3.14×(20÷2)2]
老师却认为是错误的,乐乐的方法错在哪里?请你列出正确的算式,不计算。(5分)
4.小明为了测量出一只乌龟的体积,按如下步骤进行了操作:①找来一个圆柱形玻璃杯,量得底面周长是25.12 cm;②在玻璃杯中装入一定量的水,量得水面的高度是10 cm;③将乌龟放入水中(完全浸没水中,水未溢出),再次量得水面的高度是12 cm。如果玻璃杯的厚度忽略不计,这只乌龟的体积是多少立方厘米?(5分)
5.一种压路机的滚筒是圆柱形,筒宽1.5 m,底面直径是0.8 m。这种压路机每分向前滚动20周。这种压路机15分压路多少平方米?(6分)
6.为了响应“绿色环保,合理利用资源”号召,李叔叔在养殖场挖了一个圆柱形沼气池,底面周长为25.12 m,深2.5 m。
(1)这个沼气池的占地面积是多少平方米?(3分)
(2)如果在沼气池的侧面和底部抹水泥,抹水泥的面积是多少平方米?(3分)
(3)沼气池的容积是多少升?(3分)
★挑战题:天才的你,试一试。(10分)
一段圆柱形木料,如果截成两个小圆柱,表面积增加25.12 dm2,如果沿直径劈成两半,表面积增加16 dm2,这段圆柱形木料的表面积是多少?
答案
一、1.656 3.22 8.05 5.025 5025 2.6
3.12.56 5 4.3140
5.28.26 22.608立方米【点拨】第二个空别忘了带单位。
6.9 7.圆锥 25.12 8.10 9.0.785
10.6 【点拨】本题考查等底等高的圆柱与圆锥体积关系的实际应用。圆柱与圆锥等底等高,则圆柱体积是圆锥体积的3倍。观察题中图形可知,瓶中的果汁可以看成一个高为2h的圆柱,所以它的体积是圆锥形玻璃杯可盛果汁体积的3×2=6倍,则把瓶中的果汁倒入这个圆锥形玻璃杯中,可以倒满6杯。
二、1.A 2.B 3.C 4.B 5.D 6.B 7.C
8.B 【点拨】本题考查已知圆锥的底面直径和高求圆锥的体积的实际应用。根据题意,知沙漏由两个完全相同的圆锥组成,一个圆锥的底面直径是8 cm,高是15 cm,所以沙漏的容积是×3.14×
(8÷2)2×15×2=502.4(cm3)。
三、1. (1)3×3×3.14×2=56.52(cm2)
3×2×3.14×6.5=122.46(cm2)
56.52+122.46=178.98(cm2)
(2)( 6÷2)2×3.14+6×8+6×3.14×8÷2=151.62(cm2)
2.3.14×52×20+3.14×52×15×=1962.5(cm3)
四、1.
2.(8÷2)2×3.14×8=401.92(dm3)
五、1.淘气和奇思的说法正确,妙想的说法错误。设铁桶的底面半径是r,高是h,则它的容积V=πr2h。
第一堆沙子的体积V1=πr2h<πr2h,能装下。
第二堆沙子的体积V2=πr2×2h=πr2h<πr2h,能装下。
第三堆沙子的体积V3=π×(2r)2×h=πr2h>πr2h,不能装下。
2.5×8=40(cm) 5×3=15(cm)
40×15×13=7800(cm3)
答:这个箱子内部的长、宽、高分别是40 cm、15 cm、13 cm;这个箱子的容积是7800 cm3。
3.错在没有把圆锥的体积除以。
正确算式为10×10×10÷÷
4.25.12÷3.14÷2=4(cm)
3.14×42×(12-10)=100.48(cm3)
答:这只乌龟的体积是100.48 cm3。
5.滚筒底面周长:0.8×3.14=2.512(m)
每分滚动的路程:2.512×20=50.24(m)
15分滚动的路程:50.24×15=753.6(m)
15分压路的面积:753.6×1.5=1130.4(m2)
答:这种压路机15分压路1130.4 m2。
6.(1)(25.12÷3.14÷2)2×3.14=50.24(m2)
答:这个沼气池的占地面积是50.24 m2。
(2)25.12×2.5+50.24=113.04(m2)
答:抹水泥的面积是113.04 m2。
(3)50.24×2.5=125.6(m3)
125.6 m3=125600 L
答:沼气池的容积是125600 L。
挑战题:25.12÷2=12.56(dm2)
12.56÷3.14=4(dm2)底面半径为2 dm。
16÷2÷(2×2)=2(dm)
25.12+2×2×3.14×2=50.24(dm2)
答:这段圆柱形木料的表面积为50.24 dm2。
【点拨】截成两个小圆柱,表面积增加25.12 dm2,说明25.12 dm2是两个横截面的面积,也就是2个底面的面积。如果沿直径劈成两半,表面积增加16 dm2,说明以直径和高为相邻两边的两个长方形的面积和是16 dm2。
第一单元 圆柱与圆锥
一、认真审题,填一填。(第1小题4分,其余每小题2分,共22分)
1.6.56 m2=( )dm2 3 dm2 22 cm2=( )dm2
8 L 50 mL=( )L 5 m3 25 dm3=( )m3=( )L
2.一个圆锥的体积是18.84 dm3,底面积是9.42 dm2,高是( )dm。
3.一个圆柱体,它的底面半径是2厘米,高是5厘米,将它沿底面半径分成若干等份,然后拼成一个近似的长方体,这个长方体的底面积是( )平方厘米,高是( )厘米。
4.如图,一个底面直径为20 cm,长为50 cm的圆柱形通风管,沿着地面滚动一周,滚过的面积是( )cm2。
5.一个近似于圆锥形状的野营帐篷(如图所示),它的底面半径是3米,高是2.4米。帐篷的占地面积是( )平方米,它的体积是( )。
6.用一块长28.26厘米、宽15.7厘米的长方形铁皮,应配上直径为( )厘米的圆形铁皮,可以做成一个容积最大的容器。
7.如图是一个直角三角形,以6 cm长的直角边所在直线为轴旋转一周,所得到的图形是( ),它的体积是( )cm3。
8.用一块轻黏土可以捏成一个底面积是12 cm2,高是5 cm的长方体。如果把这块轻黏土捏成底面积是6 cm2的圆柱,这个圆柱的高是( )cm。
9.一个圆柱形水桶有点破损(水平放置),底面内直径为10 cm,高为12 cm,破损处的最小高度是10 cm,该桶最多能装
( )L水。
10.右图是一瓶已经喝了一些的果汁和一个圆锥形玻璃杯。如果把瓶中的果汁倒入这个圆锥形玻璃杯中,可以倒满( )杯。(容器厚度忽略不计)
二、仔细推敲,选一选。(将正确答案的序号填在括号里)(每小题2分,共16分)
1.把如图所示的圆柱切开,得到的切面的形状是( )。
2.如图,一个圆柱切拼成一个近似长方体后,( )。
A.表面积不变,体积不变
B.表面积变大,体积不变
C.表面积变大,体积变大
D.表面积不变,体积变大
3.下面说法正确的是( )。
A.圆柱的侧面展开图一定是长方形
B.圆锥的高是圆柱的高的3倍,它们的体积一定相等
C.圆柱的高扩大到原来的2倍,要使体积不变,底面积应该缩小到原来的
D.两个圆柱的侧面积相等,它们的体积一定相等
4.芳芳有一个圆锥形容器和一个圆柱形容器,它们等底等高,她将圆柱形容器装满水后倒入圆锥形容器,从圆锥形容器中溢出36.2毫升水。圆锥形容器内有水( )毫升。
A.36.2 B.18.1 C.54.3 D.108.6
5.如图,有圆柱和圆锥共4个,关于它们的体积,下列说法错误的是( )。
A.①和④的体积相等
B.②的体积是①的3倍
C.②的体积是④的3倍
D.①和③的体积相等
6.一个长方形的长是6厘米,宽是4厘米。如图所示,以长所在的直线为轴旋转一周形成圆柱甲,以宽所在的直线为轴旋转一周形成圆柱乙。下列说法中正确的是( )。
①圆柱甲的底面积比圆柱乙的底面积大。
②圆柱甲的侧面积和圆柱乙的侧面积相等。
③圆柱甲的表面积与圆柱乙的表面积相等。
④圆柱甲的体积比圆柱乙的体积小。
A.①③ B.②④ C.①② D.③④
7.一个长方体包装盒的长是32厘米,宽是2厘米,高是1厘米。圆柱形零件的底面直径是2厘米,高是1厘米。这个包装盒内最多能放( )个零件。
A.32 B.25 C.16 D. 8
8.沙漏又称沙钟,是我国古代一种计量时间的仪器,它是根据流沙从一个容器漏到另一个容器的时间来计时的,右图是一个沙漏(由两个完全相同的圆锥组成)的示意图(单位:cm),这个沙漏的容积是( )cm3。
A.251.2 B.502.4 C.753.6
三、细心的你,算一算。(共16分)
1.计算它们的表面积。(单位:cm)(8分)
2.计算它的体积。(单位:cm)(8分)
四、动手操作,我能行。(共10分)
李师傅想用下面的长方形铁皮制作一个无盖的圆柱形水桶,且使这个水桶的容积尽可能大 (接头处忽略不计)。
1.请你画一画并标出底面和侧面。(5分)
2.算出水桶的容积。(5分)
五、聪明的你,答一答。(共36分)
1.如图,要把下面三堆圆锥形的沙子分别装在圆柱形的铁桶中(铁桶厚度忽略不计)。
下面是三名同学经过测量后得到的结论。
淘气说:“第一堆沙子和铁桶等底等高,能装下。”
奇思说:“第二堆沙子和铁桶等底,高是铁桶的2倍,能装下。”
妙想说:“第三堆沙子和铁桶等高,底面直径是铁桶的2倍,能装下。”
你认为谁的说法正确?谁的说法错误?请说明理由。(5分)
2.圆柱形的核桃露罐的底面直径是5 cm,高是13 cm。将24罐这种核桃露放在长方体箱子里,每排放8罐,放3排,刚好合适。这个箱子内部的长、宽、高分别是多少厘米?这个箱子的容积是多少?(6分)
3.把一块棱长10厘米的正方体铁块熔铸成一块底面直径是20厘米的圆锥形铁块。这块圆锥形铁块的高约是多少?
解答这道题时,乐乐列出了下面的综合算式:
10×10×10÷[3.14×(20÷2)2]
老师却认为是错误的,乐乐的方法错在哪里?请你列出正确的算式,不计算。(5分)
4.小明为了测量出一只乌龟的体积,按如下步骤进行了操作:①找来一个圆柱形玻璃杯,量得底面周长是25.12 cm;②在玻璃杯中装入一定量的水,量得水面的高度是10 cm;③将乌龟放入水中(完全浸没水中,水未溢出),再次量得水面的高度是12 cm。如果玻璃杯的厚度忽略不计,这只乌龟的体积是多少立方厘米?(5分)
5.一种压路机的滚筒是圆柱形,筒宽1.5 m,底面直径是0.8 m。这种压路机每分向前滚动20周。这种压路机15分压路多少平方米?(6分)
6.为了响应“绿色环保,合理利用资源”号召,李叔叔在养殖场挖了一个圆柱形沼气池,底面周长为25.12 m,深2.5 m。
(1)这个沼气池的占地面积是多少平方米?(3分)
(2)如果在沼气池的侧面和底部抹水泥,抹水泥的面积是多少平方米?(3分)
(3)沼气池的容积是多少升?(3分)
★挑战题:天才的你,试一试。(10分)
一段圆柱形木料,如果截成两个小圆柱,表面积增加25.12 dm2,如果沿直径劈成两半,表面积增加16 dm2,这段圆柱形木料的表面积是多少?
答案
一、1.656 3.22 8.05 5.025 5025 2.6
3.12.56 5 4.3140
5.28.26 22.608立方米【点拨】第二个空别忘了带单位。
6.9 7.圆锥 25.12 8.10 9.0.785
10.6 【点拨】本题考查等底等高的圆柱与圆锥体积关系的实际应用。圆柱与圆锥等底等高,则圆柱体积是圆锥体积的3倍。观察题中图形可知,瓶中的果汁可以看成一个高为2h的圆柱,所以它的体积是圆锥形玻璃杯可盛果汁体积的3×2=6倍,则把瓶中的果汁倒入这个圆锥形玻璃杯中,可以倒满6杯。
二、1.A 2.B 3.C 4.B 5.D 6.B 7.C
8.B 【点拨】本题考查已知圆锥的底面直径和高求圆锥的体积的实际应用。根据题意,知沙漏由两个完全相同的圆锥组成,一个圆锥的底面直径是8 cm,高是15 cm,所以沙漏的容积是×3.14×
(8÷2)2×15×2=502.4(cm3)。
三、1. (1)3×3×3.14×2=56.52(cm2)
3×2×3.14×6.5=122.46(cm2)
56.52+122.46=178.98(cm2)
(2)( 6÷2)2×3.14+6×8+6×3.14×8÷2=151.62(cm2)
2.3.14×52×20+3.14×52×15×=1962.5(cm3)
四、1.
2.(8÷2)2×3.14×8=401.92(dm3)
五、1.淘气和奇思的说法正确,妙想的说法错误。设铁桶的底面半径是r,高是h,则它的容积V=πr2h。
第一堆沙子的体积V1=πr2h<πr2h,能装下。
第二堆沙子的体积V2=πr2×2h=πr2h<πr2h,能装下。
第三堆沙子的体积V3=π×(2r)2×h=πr2h>πr2h,不能装下。
2.5×8=40(cm) 5×3=15(cm)
40×15×13=7800(cm3)
答:这个箱子内部的长、宽、高分别是40 cm、15 cm、13 cm;这个箱子的容积是7800 cm3。
3.错在没有把圆锥的体积除以。
正确算式为10×10×10÷÷
4.25.12÷3.14÷2=4(cm)
3.14×42×(12-10)=100.48(cm3)
答:这只乌龟的体积是100.48 cm3。
5.滚筒底面周长:0.8×3.14=2.512(m)
每分滚动的路程:2.512×20=50.24(m)
15分滚动的路程:50.24×15=753.6(m)
15分压路的面积:753.6×1.5=1130.4(m2)
答:这种压路机15分压路1130.4 m2。
6.(1)(25.12÷3.14÷2)2×3.14=50.24(m2)
答:这个沼气池的占地面积是50.24 m2。
(2)25.12×2.5+50.24=113.04(m2)
答:抹水泥的面积是113.04 m2。
(3)50.24×2.5=125.6(m3)
125.6 m3=125600 L
答:沼气池的容积是125600 L。
挑战题:25.12÷2=12.56(dm2)
12.56÷3.14=4(dm2)底面半径为2 dm。
16÷2÷(2×2)=2(dm)
25.12+2×2×3.14×2=50.24(dm2)
答:这段圆柱形木料的表面积为50.24 dm2。
【点拨】截成两个小圆柱,表面积增加25.12 dm2,说明25.12 dm2是两个横截面的面积,也就是2个底面的面积。如果沿直径劈成两半,表面积增加16 dm2,说明以直径和高为相邻两边的两个长方形的面积和是16 dm2。
