人教版九年级数学下册 26.2实际问题与反比例函数 同步训练(word版含答案)
文档属性
| 名称 | 人教版九年级数学下册 26.2实际问题与反比例函数 同步训练(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 291.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 00:00:00 | ||
图片预览


文档简介
人教版九年级数学下册26.2实际问题与反比例函数同步训练
一、单选题
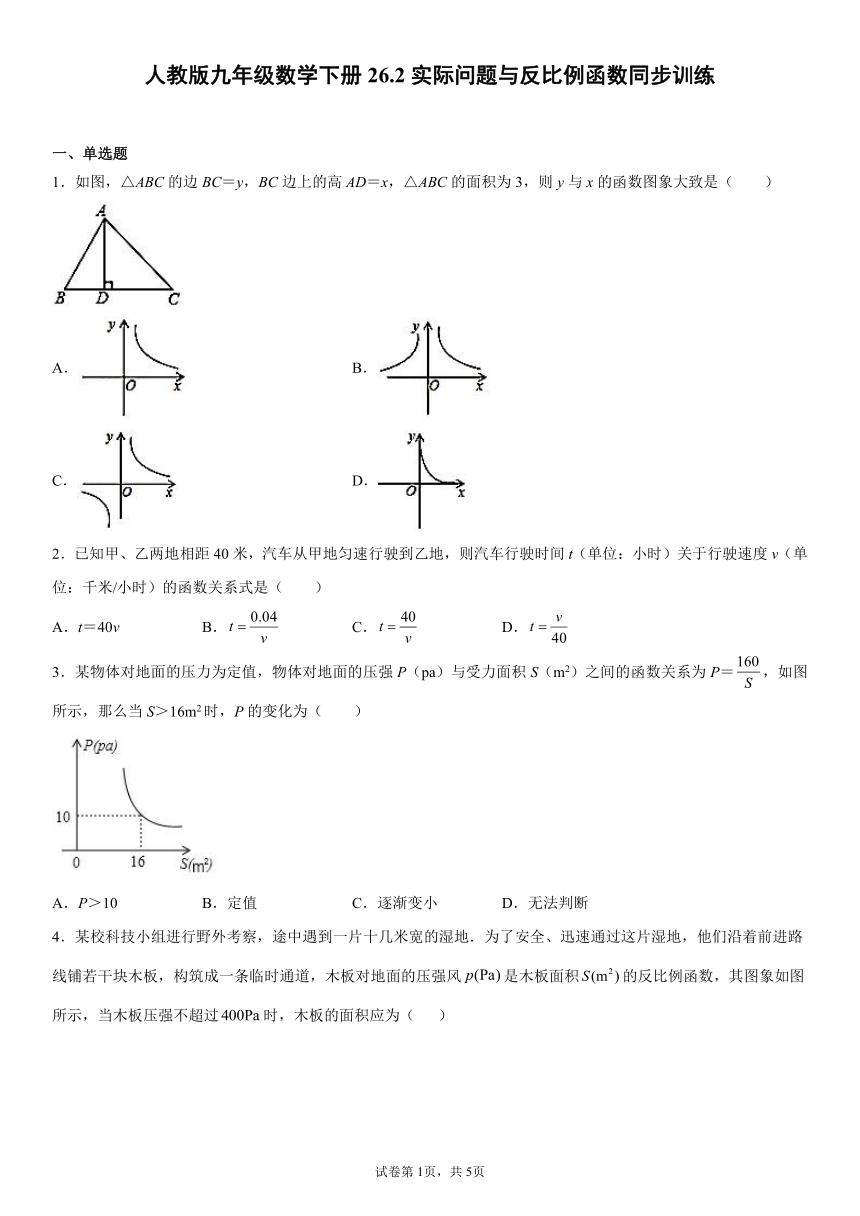
1.如图,△ABC的边BC=y,BC边上的高AD=x,△ABC的面积为3,则y与x的函数图象大致是( )
A. B.
C. D.
2.已知甲、乙两地相距40米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B. C. D.
3.某物体对地面的压力为定值,物体对地面的压强P(pa)与受力面积S(m2)之间的函数关系为P=,如图所示,那么当S>16m2时,P的变化为( )
A.P>10 B.定值 C.逐渐变小 D.无法判断
4.某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强风是木板面积的反比例函数,其图象如图所示,当木板压强不超过时,木板的面积应为( )
A.不大于 B.不小于 C.不大于 D.不小于
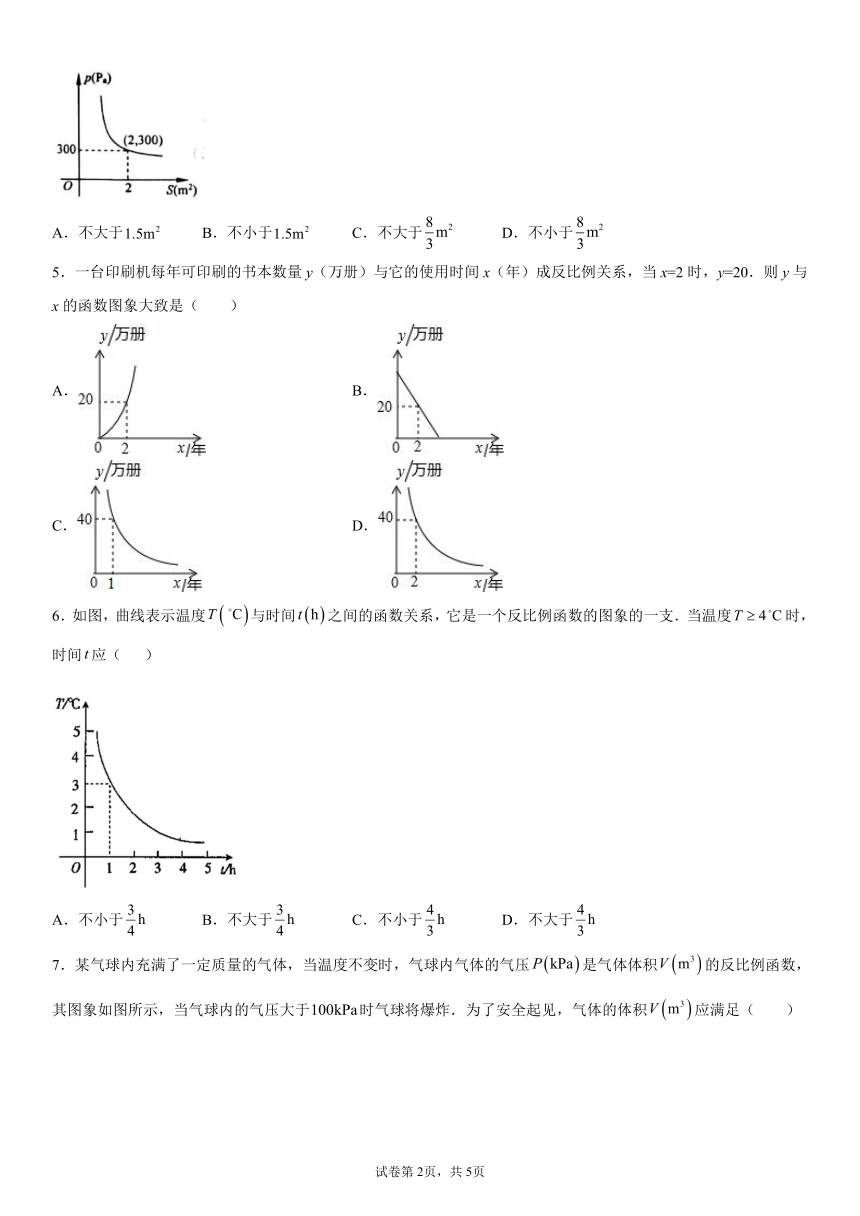
5.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
6.如图,曲线表示温度与时间之间的函数关系,它是一个反比例函数的图象的一支.当温度时,时间应( )
A.不小于 B.不大于 C.不小于 D.不大于
7.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示,当气球内的气压大于时气球将爆炸.为了安全起见,气体的体积应满足( )
A. B. C. D.
8.某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地.当人和木板对湿地的压力一定时,人和木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数,其图象如图,点A在反比例函数图象上,坐标是(8,30),当压强P(Pa)是4800Pa时,木板面积为( )m2
A.0.5 B.2 C.0.05 D.20
二、填空题
9.一定质量的氧气,它的密度(kg/m3)是它的体积(m3)的反比例函数,当V=20m3时,kg/m3,当V=40m3时,______kg/m3.
10.一个水池装水12m3,如果从水管中每小时流出m3的水,经过h可以把水放完,那么 与的函数关系式是______,自变量的取值范围是______.
11.一水桶的下底面积是桶盖面积的2倍,如果将其底朝下放在桌上,它对桌面的压强是500Pa.翻过来放,对桌面的压强是_____________.
12.近视眼镜的度数y(度)与镜片焦距x()成反比例,已知500度的近视眼镜镜片的焦距是,则y与x之间的函数表达式是______.
13.由电学欧姆定律知,电压不变时,电流强度I与电阻R成反比例,已知电压不变,电阻时,电流强度.则
(1)电压______V;(2)I与R的函数关系式为____________;
(3)当时的电流强度________A;
(4)当时,电阻_________.
14.已知近视眼镜的度数D(度)与镜片焦距f(米)成反比例关系,且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜,经过一段时间的矫正治疗后,现在只需戴镜片焦距为0.4米的眼镜了,则小慧所戴眼镜的度数降低了 ___度.
15.小明要把一篇文章录入电脑,所需时间与录入文字的速度(字)之间的反比例函数关系如图所示,如果小明要在内完成录入任务,则小明录入文字的速度至少为______字.
16.某工程队为教学楼贴瓷砖,已知楼体外表面积为5×103m2.所需的瓷砖块数n与每块瓷砖的面积S(单位:m2)的函数关系式为________.
三、解答题
17.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体V(立方米)的反比例函数,其图象如图所示.
(1)求该反比例函数的关系式;
(2)当气球的体积是0.8立方米时,气球内的气压是多少千帕?
18.用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系.某天,小金、小东放学回家后各自洗一件完全相同的衣服,漂洗时,小金每次用水约6升,小东每次用水约5升,他们都用了5克洗衣粉,第一次漂洗后,小金的衣服残留的洗衣粉还有1.5克,小东的衣服残留的洗衣粉还有2克.
(1)分别求出小金、小东衣服漂洗后洗衣粉残留量关于次数的函数解析式.
(2)已知洗衣粉的残留量降至0.35克时,便视为衣服漂洗干净,若以把衣服洗干净为前提,节约用水为目标,判断小金和小东两种漂洗方法用水量的大小,并说明理由.
19.如图,李老师准备用篱笆围建一个面积为60m2的矩形花圃ABCD,其中一边AB靠墙.
(1)设AD的长为x米,DC的长为y米,求y与x之间的函数关系式;
(2)当矩形花圃ABCD的相邻两边之比是0.6时(接近黄金分割),花圃最美观.若围成矩形花圃ABCD的三边篱笆总长不超过24m,且为了美观,求此时篱笆AD的长.
20.为应对全球爆发的新冠疫情,某疫苗生产企业于2021年1月份开始了技术改造,其月生产数量(万支)与月份之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
(1)该疫苗生产企业4月份的生产数量为多少万支?
(2)该疫苗生产企业有多少个月的月生产数量不超过90万支?
参考答案
1.A
2.B
3.C
4.B
5.C
6.B
7.C
8.C
9.0.68
10. >0
11.1000Pa
12.
13.
14.150
15.
16.n=
17.(1)P=;(2)200千帕
18.(1)小金: 小东:;(2)小金的用水量与小东的用水量一样多。
19.(1);(2)6米
20.1)该疫苗生产企业4月份的生产数量为45万支;(2)该疫苗生产企业有6个月的月生产数量不超过90万支.
试卷第4页,共5页
试卷第5页,共5页
一、单选题
1.如图,△ABC的边BC=y,BC边上的高AD=x,△ABC的面积为3,则y与x的函数图象大致是( )
A. B.
C. D.
2.已知甲、乙两地相距40米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B. C. D.
3.某物体对地面的压力为定值,物体对地面的压强P(pa)与受力面积S(m2)之间的函数关系为P=,如图所示,那么当S>16m2时,P的变化为( )
A.P>10 B.定值 C.逐渐变小 D.无法判断
4.某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强风是木板面积的反比例函数,其图象如图所示,当木板压强不超过时,木板的面积应为( )
A.不大于 B.不小于 C.不大于 D.不小于
5.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
6.如图,曲线表示温度与时间之间的函数关系,它是一个反比例函数的图象的一支.当温度时,时间应( )
A.不小于 B.不大于 C.不小于 D.不大于
7.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示,当气球内的气压大于时气球将爆炸.为了安全起见,气体的体积应满足( )
A. B. C. D.
8.某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地.当人和木板对湿地的压力一定时,人和木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数,其图象如图,点A在反比例函数图象上,坐标是(8,30),当压强P(Pa)是4800Pa时,木板面积为( )m2
A.0.5 B.2 C.0.05 D.20
二、填空题
9.一定质量的氧气,它的密度(kg/m3)是它的体积(m3)的反比例函数,当V=20m3时,kg/m3,当V=40m3时,______kg/m3.
10.一个水池装水12m3,如果从水管中每小时流出m3的水,经过h可以把水放完,那么 与的函数关系式是______,自变量的取值范围是______.
11.一水桶的下底面积是桶盖面积的2倍,如果将其底朝下放在桌上,它对桌面的压强是500Pa.翻过来放,对桌面的压强是_____________.
12.近视眼镜的度数y(度)与镜片焦距x()成反比例,已知500度的近视眼镜镜片的焦距是,则y与x之间的函数表达式是______.
13.由电学欧姆定律知,电压不变时,电流强度I与电阻R成反比例,已知电压不变,电阻时,电流强度.则
(1)电压______V;(2)I与R的函数关系式为____________;
(3)当时的电流强度________A;
(4)当时,电阻_________.
14.已知近视眼镜的度数D(度)与镜片焦距f(米)成反比例关系,且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜,经过一段时间的矫正治疗后,现在只需戴镜片焦距为0.4米的眼镜了,则小慧所戴眼镜的度数降低了 ___度.
15.小明要把一篇文章录入电脑,所需时间与录入文字的速度(字)之间的反比例函数关系如图所示,如果小明要在内完成录入任务,则小明录入文字的速度至少为______字.
16.某工程队为教学楼贴瓷砖,已知楼体外表面积为5×103m2.所需的瓷砖块数n与每块瓷砖的面积S(单位:m2)的函数关系式为________.
三、解答题
17.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气体V(立方米)的反比例函数,其图象如图所示.
(1)求该反比例函数的关系式;
(2)当气球的体积是0.8立方米时,气球内的气压是多少千帕?
18.用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系.某天,小金、小东放学回家后各自洗一件完全相同的衣服,漂洗时,小金每次用水约6升,小东每次用水约5升,他们都用了5克洗衣粉,第一次漂洗后,小金的衣服残留的洗衣粉还有1.5克,小东的衣服残留的洗衣粉还有2克.
(1)分别求出小金、小东衣服漂洗后洗衣粉残留量关于次数的函数解析式.
(2)已知洗衣粉的残留量降至0.35克时,便视为衣服漂洗干净,若以把衣服洗干净为前提,节约用水为目标,判断小金和小东两种漂洗方法用水量的大小,并说明理由.
19.如图,李老师准备用篱笆围建一个面积为60m2的矩形花圃ABCD,其中一边AB靠墙.
(1)设AD的长为x米,DC的长为y米,求y与x之间的函数关系式;
(2)当矩形花圃ABCD的相邻两边之比是0.6时(接近黄金分割),花圃最美观.若围成矩形花圃ABCD的三边篱笆总长不超过24m,且为了美观,求此时篱笆AD的长.
20.为应对全球爆发的新冠疫情,某疫苗生产企业于2021年1月份开始了技术改造,其月生产数量(万支)与月份之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
(1)该疫苗生产企业4月份的生产数量为多少万支?
(2)该疫苗生产企业有多少个月的月生产数量不超过90万支?
参考答案
1.A
2.B
3.C
4.B
5.C
6.B
7.C
8.C
9.0.68
10. >0
11.1000Pa
12.
13.
14.150
15.
16.n=
17.(1)P=;(2)200千帕
18.(1)小金: 小东:;(2)小金的用水量与小东的用水量一样多。
19.(1);(2)6米
20.1)该疫苗生产企业4月份的生产数量为45万支;(2)该疫苗生产企业有6个月的月生产数量不超过90万支.
试卷第4页,共5页
试卷第5页,共5页
