2021-2022学年湘教版八年级数学上册2.1.2 三角形的高、角平分线和中线 同步测试卷 (Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学上册2.1.2 三角形的高、角平分线和中线 同步测试卷 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 322.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 19:26:48 | ||
图片预览



文档简介
2.1.2 三角形的高、角平分线和中线同步测试卷 2021-2022学年湘教版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共27分)
画ABC的高BE,以下画图正确的是( )
A. B.
C. D.
如图,在ABC中,CDBC于点C,点D在AB的延长线上,则CD是ABC( )
A. 边上的高 B. 边上的高 C. 边上的高 D. 以上都不对
如图,CD、CE、CF分别是ABC的高、角平分线、中线,则下列各式错误的是( )
A. B.
C. D.
如图,以AD为高的三角形有( )
A. 个 B. 个
C. 个 D. 个
如图,1=2,3=4,则下列结论正确的有( )
AD平分BAF;AF平分BAC;AE平分DAF;AF平分DAC;AE平分BAC.
A. 个 B. 个 C. 个 D. 个
三角形的重心是三角形的( )
A. 三条角平分线的交点
B. 一条边的中线与另一边的高的交点
C. 三条高线的交点
D. 三条中线的交点
下列说法正确的是( )
三角形的角平分线是射线;
三角形的三条角平分线都在三角形内部,且交于同一点;
三角形的三条高都在三角形内部;
三角形的一条中线把该三角形分成面积相等的两部分.
A. B. C. D.
一定在ABC内部的线段是( )
A. 锐角三角形的三条高、三条角平分线、三条中线
B. 钝角三角形的三条高、三条中线、一条角平分线
C. 任意三角形的一条中线、二条角平分线、三条高
D. 直角三角形的三条高、三条角平分线、三条中线
如图,在ABC中,D,E分别是BC,AD的中点,则图中与ABE的面积相等的三角形有( )
A. 个 B. 个
C. 个 D. 个
二、填空题(本大题共4小题,共12分)
如图,在ABC中,AB=18,AC=15,AD为中线,则ABD与ACD的周长之差为 .
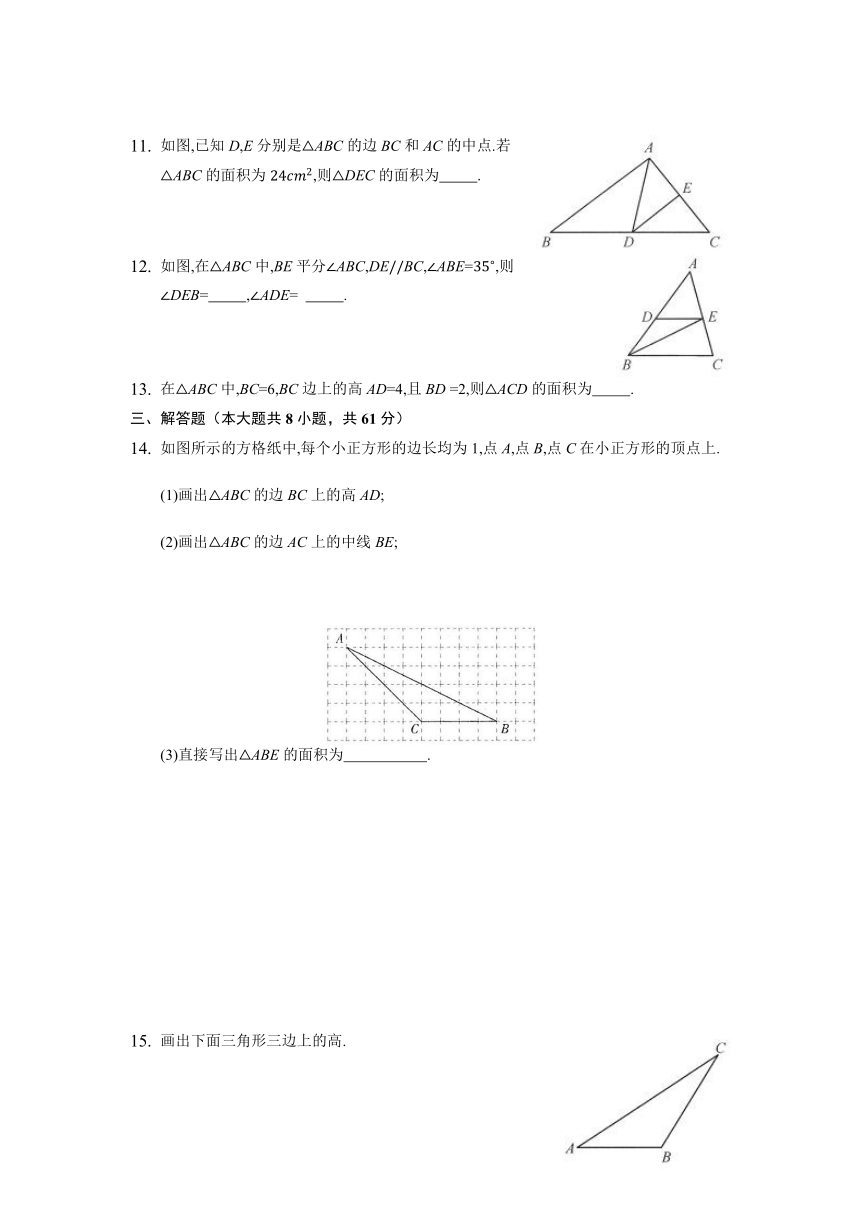
如图,已知D,E分别是ABC的边BC和AC的中点.若ABC的面积为,则DEC的面积为 .
如图,在ABC中,BE平分ABC,DEBC,ABE=,则DEB= ,ADE= .
在ABC中,BC=6,BC边上的高AD=4,且BD =2,则ACD的面积为 .
三、解答题(本大题共8小题,共61分)
如图所示的方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出ABC的边BC上的高AD;
(2)画出ABC的边AC上的中线BE;
(3)直接写出ABE的面积为 .
画出下面三角形三边上的高.
如图,ABC中,BC、AC边上的高分别是AD、BE.已知BC=5cm,AD=6cm,AC=7cm,求BE的长.
如图,在ABC中,已知点D,E,F分别为边BC, AD,CE的中点,且=,求阴影部分的面积.
如图,AD为ABC的中线,BE为ABD的角平分线.
(1)若ABE=,求ABD的度数;
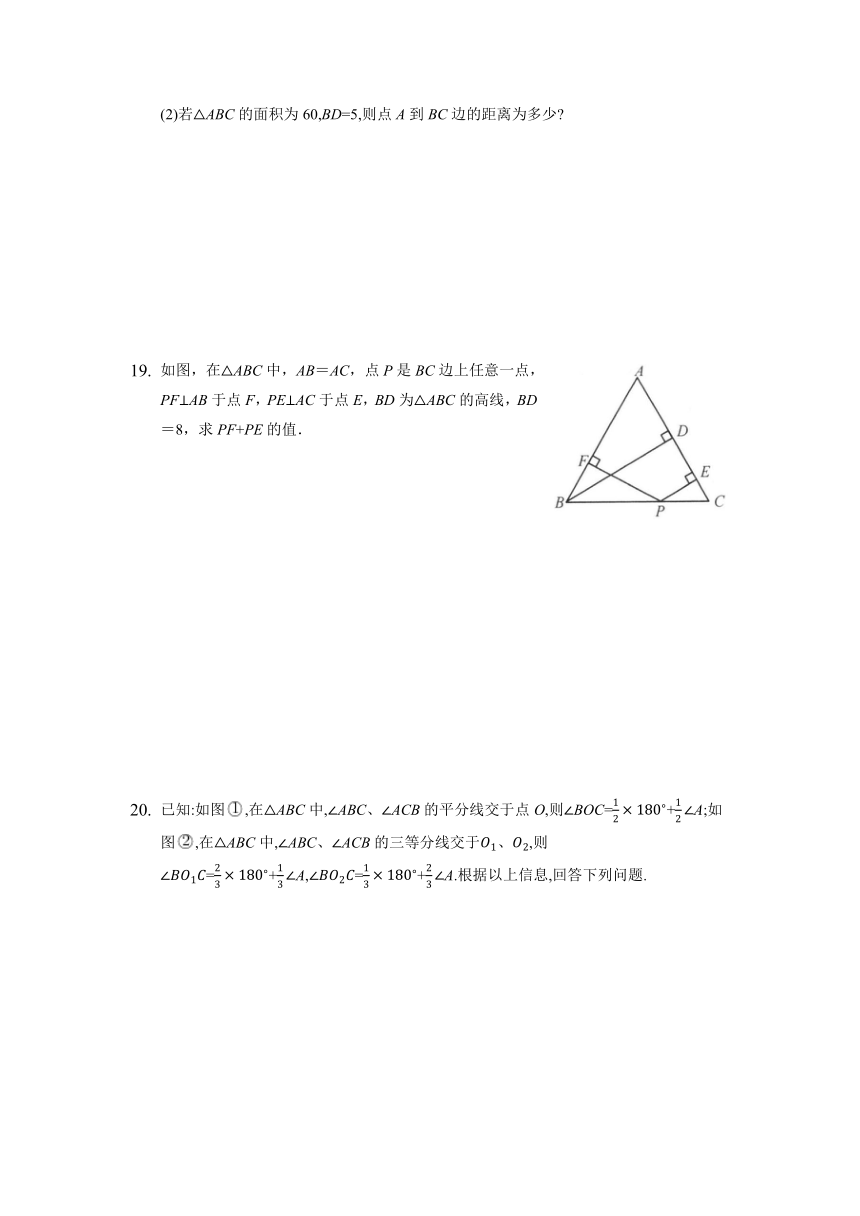
(2)若ABC的面积为60,BD=5,则点A到BC边的距离为多少
如图,在△ABC中,AB=AC,点P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,BD=8,求PF+PE的值.
已知:如图,在ABC中,ABC、ACB的平分线交于点O,则BOC=+A;如图,在ABC中,ABC、ACB的三等分线交于、,则=+A,=+A.根据以上信息,回答下列问题.
(1)请猜想它的规律.如图,n等分时,内部有(n-1)个点,则= ,= (用含n的代数式表示);
(2)根据你的猜想,取n=4时,证明的度数成立.
在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于点D.
(1)如图1,当点F与点A重合,且∠C=50°,∠B=30°时,求∠EFD的度数,并直接写出∠EFD与之间的数量关系;
(2)如图2,当点F在线段AE上(不与点A重合),∠EFD与∠C-∠B有怎样的数量关系?并说明理由;
(3)当点F在△ABC外部时,在图3中画出符合题意的图形,并直接写出∠EFD与∠C-∠B的数量关系.
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】A
9.【答案】B
10.【答案】 3
11.【答案】
12.【答案】
13.【答案】 8或16
14.【答案】解:(1)如图所示,线段AD即为所求.
(2)如图所示,线段BE即为所求.
(3)ABE的面积为4.
15.【答案】
如图所示:CE,BD,AF即为所求.
16.【答案】解:AD、BE分别是ABC的边BC、AC上的高,
=BCAD=ACBE,
BCAD=ACBE,
BC=5cm,AD=6cm,AC=7cm,
BE==cm.
17.【答案】解:
因为D是边BC的中点,所以===4=2().
因为E是AD的中点,所以==, ==.所以=+=.
又因为F是CE的中点,所以==.
18.【答案】解:
(1)因为BE为ABD的角平分线,ABE=,所以ABD=2ABE=.
(2)点A到BC边的距离为12.
19.【答案】解:连接PA.
∵S△ABC=S△APB+S△APC,
∴.
∵AB=AC,
∴BD=PF+PE.
∴PF+PE=8.
20.【答案】解:(1)=+A;
=+A.
(2)当n=4时,=+A.
证明:
=-(+)
=-(ABC+ACB)
=-(-A)
=-+A
=+A,
当n=4时,=+A.
21.【答案】解:(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°.
∵AE是∠BAC的平分线,
∴.
∵FD⊥BC,
∴∠FDC=90°.
∴∠DAC=180°-90°-50°=40°.
∴∠EFD=∠CAE-∠CAD=50°-40°=10°.
∠EFD与之间的数量关系为.
(2).
理由:过A作AM⊥BC于M,
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C.
∵AE是∠BAC的平分线,
∴.
∵AM⊥BC,
∴∠AMC=90°.
∴∠MAC=180°-90°-∠C=90°-∠C.
∴.
∵AM⊥BC,FD⊥BC,
∴AM // FD.
∴.
(3)如图,.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共27分)
画ABC的高BE,以下画图正确的是( )
A. B.
C. D.
如图,在ABC中,CDBC于点C,点D在AB的延长线上,则CD是ABC( )
A. 边上的高 B. 边上的高 C. 边上的高 D. 以上都不对
如图,CD、CE、CF分别是ABC的高、角平分线、中线,则下列各式错误的是( )
A. B.
C. D.
如图,以AD为高的三角形有( )
A. 个 B. 个
C. 个 D. 个
如图,1=2,3=4,则下列结论正确的有( )
AD平分BAF;AF平分BAC;AE平分DAF;AF平分DAC;AE平分BAC.
A. 个 B. 个 C. 个 D. 个
三角形的重心是三角形的( )
A. 三条角平分线的交点
B. 一条边的中线与另一边的高的交点
C. 三条高线的交点
D. 三条中线的交点
下列说法正确的是( )
三角形的角平分线是射线;
三角形的三条角平分线都在三角形内部,且交于同一点;
三角形的三条高都在三角形内部;
三角形的一条中线把该三角形分成面积相等的两部分.
A. B. C. D.
一定在ABC内部的线段是( )
A. 锐角三角形的三条高、三条角平分线、三条中线
B. 钝角三角形的三条高、三条中线、一条角平分线
C. 任意三角形的一条中线、二条角平分线、三条高
D. 直角三角形的三条高、三条角平分线、三条中线
如图,在ABC中,D,E分别是BC,AD的中点,则图中与ABE的面积相等的三角形有( )
A. 个 B. 个
C. 个 D. 个
二、填空题(本大题共4小题,共12分)
如图,在ABC中,AB=18,AC=15,AD为中线,则ABD与ACD的周长之差为 .
如图,已知D,E分别是ABC的边BC和AC的中点.若ABC的面积为,则DEC的面积为 .
如图,在ABC中,BE平分ABC,DEBC,ABE=,则DEB= ,ADE= .
在ABC中,BC=6,BC边上的高AD=4,且BD =2,则ACD的面积为 .
三、解答题(本大题共8小题,共61分)
如图所示的方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出ABC的边BC上的高AD;
(2)画出ABC的边AC上的中线BE;
(3)直接写出ABE的面积为 .
画出下面三角形三边上的高.
如图,ABC中,BC、AC边上的高分别是AD、BE.已知BC=5cm,AD=6cm,AC=7cm,求BE的长.
如图,在ABC中,已知点D,E,F分别为边BC, AD,CE的中点,且=,求阴影部分的面积.
如图,AD为ABC的中线,BE为ABD的角平分线.
(1)若ABE=,求ABD的度数;
(2)若ABC的面积为60,BD=5,则点A到BC边的距离为多少
如图,在△ABC中,AB=AC,点P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,BD=8,求PF+PE的值.
已知:如图,在ABC中,ABC、ACB的平分线交于点O,则BOC=+A;如图,在ABC中,ABC、ACB的三等分线交于、,则=+A,=+A.根据以上信息,回答下列问题.
(1)请猜想它的规律.如图,n等分时,内部有(n-1)个点,则= ,= (用含n的代数式表示);
(2)根据你的猜想,取n=4时,证明的度数成立.
在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于点D.
(1)如图1,当点F与点A重合,且∠C=50°,∠B=30°时,求∠EFD的度数,并直接写出∠EFD与之间的数量关系;
(2)如图2,当点F在线段AE上(不与点A重合),∠EFD与∠C-∠B有怎样的数量关系?并说明理由;
(3)当点F在△ABC外部时,在图3中画出符合题意的图形,并直接写出∠EFD与∠C-∠B的数量关系.
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】A
9.【答案】B
10.【答案】 3
11.【答案】
12.【答案】
13.【答案】 8或16
14.【答案】解:(1)如图所示,线段AD即为所求.
(2)如图所示,线段BE即为所求.
(3)ABE的面积为4.
15.【答案】
如图所示:CE,BD,AF即为所求.
16.【答案】解:AD、BE分别是ABC的边BC、AC上的高,
=BCAD=ACBE,
BCAD=ACBE,
BC=5cm,AD=6cm,AC=7cm,
BE==cm.
17.【答案】解:
因为D是边BC的中点,所以===4=2().
因为E是AD的中点,所以==, ==.所以=+=.
又因为F是CE的中点,所以==.
18.【答案】解:
(1)因为BE为ABD的角平分线,ABE=,所以ABD=2ABE=.
(2)点A到BC边的距离为12.
19.【答案】解:连接PA.
∵S△ABC=S△APB+S△APC,
∴.
∵AB=AC,
∴BD=PF+PE.
∴PF+PE=8.
20.【答案】解:(1)=+A;
=+A.
(2)当n=4时,=+A.
证明:
=-(+)
=-(ABC+ACB)
=-(-A)
=-+A
=+A,
当n=4时,=+A.
21.【答案】解:(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°.
∵AE是∠BAC的平分线,
∴.
∵FD⊥BC,
∴∠FDC=90°.
∴∠DAC=180°-90°-50°=40°.
∴∠EFD=∠CAE-∠CAD=50°-40°=10°.
∠EFD与之间的数量关系为.
(2).
理由:过A作AM⊥BC于M,
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C.
∵AE是∠BAC的平分线,
∴.
∵AM⊥BC,
∴∠AMC=90°.
∴∠MAC=180°-90°-∠C=90°-∠C.
∴.
∵AM⊥BC,FD⊥BC,
∴AM // FD.
∴.
(3)如图,.
第2页,共3页
同课章节目录
