5.1.3 《同位角、内错角、同旁内角》 课件(共25张PPT)
文档属性
| 名称 | 5.1.3 《同位角、内错角、同旁内角》 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 18:55:12 | ||
图片预览





文档简介
(共25张PPT)
5.1.3 同位角、
内错角、同旁内角
人教版数学 七年级下册
理解同位角、内错角、同旁内角的概念。
在简单几何图形中指出同位角、内错角、同旁内角。
通过观察、探究,培养学生观察图形的能力。
学习目标
复习巩固
01
邻补角的概念:
对顶角的概念:
对顶角的性质:
如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。
如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这两个角叫对顶角。
对顶角相等
知识回顾
新课教学
02
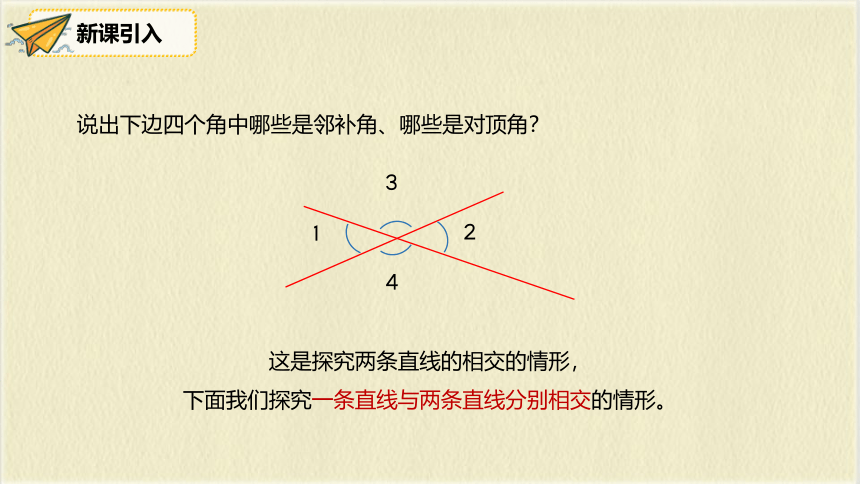
说出下边四个角中哪些是邻补角、哪些是对顶角?
1
2
3
4
这是探究两条直线的相交的情形,
下面我们探究一条直线与两条直线分别相交的情形。
新课引入
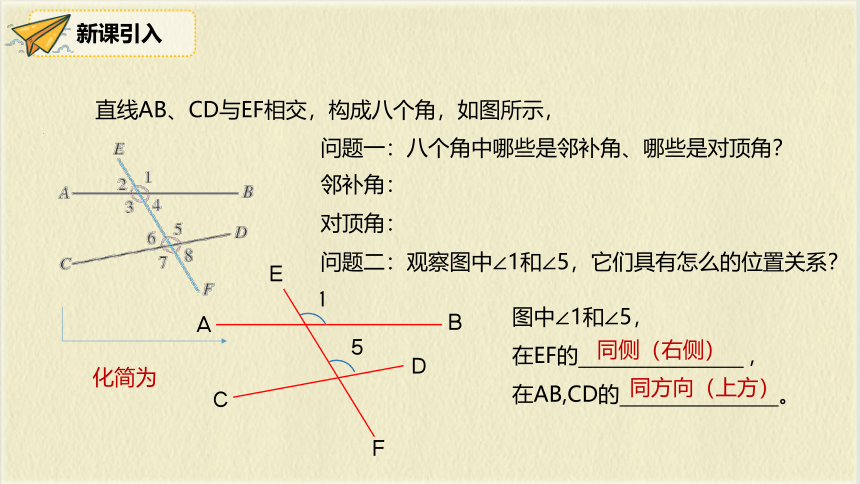
直线AB、CD与EF相交,构成八个角,如图所示,
问题一:八个角中哪些是邻补角、哪些是对顶角?
邻补角:
对顶角:
问题二:观察图中∠1和∠5,它们具有怎么的位置关系?
化简为
1
5
E
F
D
B
A
C
图中∠1和∠5,
在EF的 ,
在AB,CD的 。
同侧(右侧)
同方向(上方)
新课引入
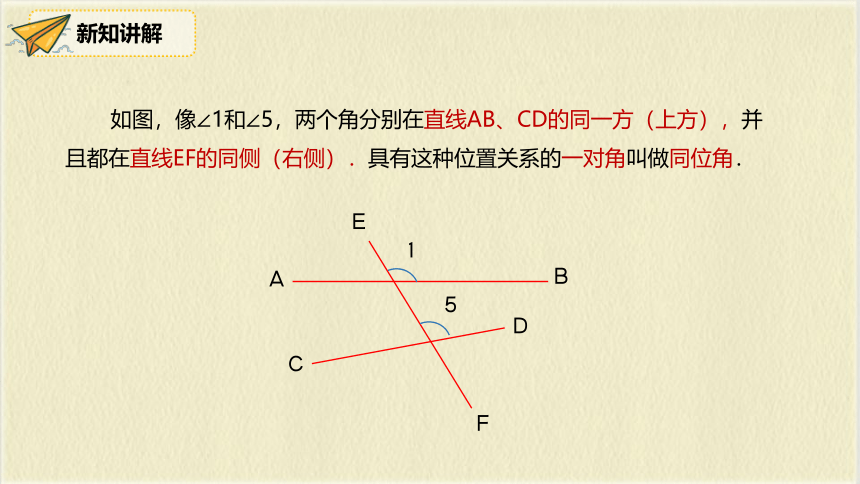
如图,像∠1和∠5,两个角分别在直线AB、CD的同一方(上方),并且都在直线EF的同侧(右侧).具有这种位置关系的一对角叫做同位角.
1
5
E
F
D
B
A
C
新知讲解
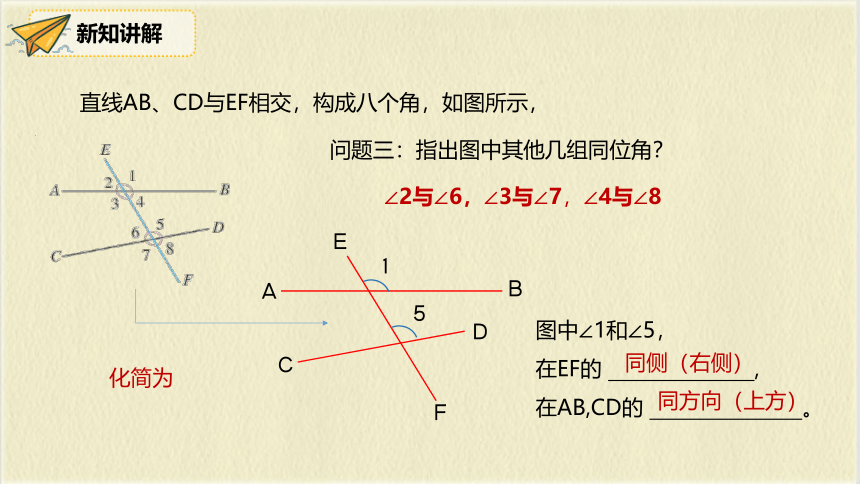
直线AB、CD与EF相交,构成八个角,如图所示,
问题三:指出图中其他几组同位角?
化简为
1
5
E
F
D
B
A
C
图中∠1和∠5,
在EF的 ,
在AB,CD的 。
同侧(右侧)
同方向(上方)
∠2与∠6,∠3与∠7,∠4与∠8
新知讲解
直线AB、CD与EF相交,构成八个角,如图所示,
问题四:观察图中∠4和∠6,它们具有怎么的位置关系?
化简为
4
6
E
F
D
B
A
C
图中∠4和∠6,
在EF的____________,
在AB,CD的____________。
两侧
内部
新知讲解
如图,像∠4和∠6,两个角分别在直线AB、CD之间,并且分别在直线EF的两侧,具有这种位置关系的一对角叫做内错角.
4
6
E
F
D
B
A
C
新知讲解
直线AB、CD与EF相交,构成八个角,如图所示,
问题五:指出图中其他几组内错角?
化简为
4
6
E
F
D
B
A
C
图中∠4和∠6,
在EF的____________,
在AB,CD的________。
两侧
内部
∠3与∠5
新知讲解
直线AB、CD与EF相交,构成八个角,如图所示,
问题六:观察图中∠3和∠6,它们具有怎么的位置关系?
化简为
3
6
E
F
D
B
A
C
图中∠3和∠6,
在EF的____________,
在AB,CD的_________。
同侧(左侧)
内部
新知讲解
3
6
E
F
D
B
A
C
如图,像∠3和∠6,两个角分别在直线AB、CD之间,并且都在直线EF的同侧,具有这种位置关系的一对角叫做同旁内角。
新知讲解
直线AB、CD与EF相交,构成八个角,如图所示,
问题七:指出图中其他几组同旁内角?
化简为
3
6
E
F
D
B
A
C
图中∠3和∠6,
在EF的____________,
在AB,CD的____________。
同侧(左侧)
内部
∠4 与∠5
新知讲解
小试牛刀
03
1.如图,直线DE、BC被直线AB所截,
1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角?
2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
(1)分别为:内错角、同旁内角、同位角
(2)∵ ∠2=∠4而∠1=∠4
∴ ∠1=∠2
∵∠3+∠4=180°而∠1=∠4
∴ ∠3+∠1=180°
∴ ∠1和∠3互补
小试牛刀
2.两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”为了便于记忆,同学们可仿照图用双手表示“三线八角”两大拇指代表被截直线,食指代表截线下列三幅图依次表示
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
小试牛刀
3.如图,下列说法错误的是( )
A.∠A与∠AEF是同旁内角 B . ∠AFE与∠BEF是内错角
C. ∠A与∠CFE是同位角 D. ∠BED与∠CFG是同位角
【答案】D
理由如下:
A. ∠A与∠AEF是同旁内角,正确
B. ∠AFE与∠BEF是内错角,正确
C. ∠A与∠CFE是同位角,正确
D. ∠BED与∠CFG是同位角,错误
小试牛刀
4.如图,下列判断中,正确的是( )
A. ∠3和∠5是同旁内角 B. ∠2和∠4是同位角
C. ∠1和∠B是内错角 D.∠5和∠B是同旁内角
【答案】D
理由如下:
A、∠3和∠5是内错角;
B、∠2和∠4无关系;
C、∠1和∠B无关系;
D、∠5和∠B是同旁内角,正确,故选D.
小试牛刀
拓展延伸
04
4.若∠α与∠β同旁内角,且∠α=50°时,则∠β的度数为( )
A.50° B.130° C.50°或130° D.无法确定
【答案】D
小试牛刀
课堂小结
05
同位角、内错角、同旁内角总结
角的 名称 角的特征 基本图形 基本图形 相同点 共同特征
同位角
同旁 内角
内错角
课堂小结
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
F
U
Z
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
谢谢观看!
注:本视频所有素材来源于网络,如有侵权,请联系我们。
5.1.3 同位角、
内错角、同旁内角
人教版数学 七年级下册
理解同位角、内错角、同旁内角的概念。
在简单几何图形中指出同位角、内错角、同旁内角。
通过观察、探究,培养学生观察图形的能力。
学习目标
复习巩固
01
邻补角的概念:
对顶角的概念:
对顶角的性质:
如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。
如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这两个角叫对顶角。
对顶角相等
知识回顾
新课教学
02
说出下边四个角中哪些是邻补角、哪些是对顶角?
1
2
3
4
这是探究两条直线的相交的情形,
下面我们探究一条直线与两条直线分别相交的情形。
新课引入
直线AB、CD与EF相交,构成八个角,如图所示,
问题一:八个角中哪些是邻补角、哪些是对顶角?
邻补角:
对顶角:
问题二:观察图中∠1和∠5,它们具有怎么的位置关系?
化简为
1
5
E
F
D
B
A
C
图中∠1和∠5,
在EF的 ,
在AB,CD的 。
同侧(右侧)
同方向(上方)
新课引入
如图,像∠1和∠5,两个角分别在直线AB、CD的同一方(上方),并且都在直线EF的同侧(右侧).具有这种位置关系的一对角叫做同位角.
1
5
E
F
D
B
A
C
新知讲解
直线AB、CD与EF相交,构成八个角,如图所示,
问题三:指出图中其他几组同位角?
化简为
1
5
E
F
D
B
A
C
图中∠1和∠5,
在EF的 ,
在AB,CD的 。
同侧(右侧)
同方向(上方)
∠2与∠6,∠3与∠7,∠4与∠8
新知讲解
直线AB、CD与EF相交,构成八个角,如图所示,
问题四:观察图中∠4和∠6,它们具有怎么的位置关系?
化简为
4
6
E
F
D
B
A
C
图中∠4和∠6,
在EF的____________,
在AB,CD的____________。
两侧
内部
新知讲解
如图,像∠4和∠6,两个角分别在直线AB、CD之间,并且分别在直线EF的两侧,具有这种位置关系的一对角叫做内错角.
4
6
E
F
D
B
A
C
新知讲解
直线AB、CD与EF相交,构成八个角,如图所示,
问题五:指出图中其他几组内错角?
化简为
4
6
E
F
D
B
A
C
图中∠4和∠6,
在EF的____________,
在AB,CD的________。
两侧
内部
∠3与∠5
新知讲解
直线AB、CD与EF相交,构成八个角,如图所示,
问题六:观察图中∠3和∠6,它们具有怎么的位置关系?
化简为
3
6
E
F
D
B
A
C
图中∠3和∠6,
在EF的____________,
在AB,CD的_________。
同侧(左侧)
内部
新知讲解
3
6
E
F
D
B
A
C
如图,像∠3和∠6,两个角分别在直线AB、CD之间,并且都在直线EF的同侧,具有这种位置关系的一对角叫做同旁内角。
新知讲解
直线AB、CD与EF相交,构成八个角,如图所示,
问题七:指出图中其他几组同旁内角?
化简为
3
6
E
F
D
B
A
C
图中∠3和∠6,
在EF的____________,
在AB,CD的____________。
同侧(左侧)
内部
∠4 与∠5
新知讲解
小试牛刀
03
1.如图,直线DE、BC被直线AB所截,
1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角?
2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
(1)分别为:内错角、同旁内角、同位角
(2)∵ ∠2=∠4而∠1=∠4
∴ ∠1=∠2
∵∠3+∠4=180°而∠1=∠4
∴ ∠3+∠1=180°
∴ ∠1和∠3互补
小试牛刀
2.两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”为了便于记忆,同学们可仿照图用双手表示“三线八角”两大拇指代表被截直线,食指代表截线下列三幅图依次表示
A.同位角、同旁内角、内错角 B.同位角、内错角、同旁内角
C.同位角、对顶角、同旁内角 D.同位角、内错角、对顶角
小试牛刀
3.如图,下列说法错误的是( )
A.∠A与∠AEF是同旁内角 B . ∠AFE与∠BEF是内错角
C. ∠A与∠CFE是同位角 D. ∠BED与∠CFG是同位角
【答案】D
理由如下:
A. ∠A与∠AEF是同旁内角,正确
B. ∠AFE与∠BEF是内错角,正确
C. ∠A与∠CFE是同位角,正确
D. ∠BED与∠CFG是同位角,错误
小试牛刀
4.如图,下列判断中,正确的是( )
A. ∠3和∠5是同旁内角 B. ∠2和∠4是同位角
C. ∠1和∠B是内错角 D.∠5和∠B是同旁内角
【答案】D
理由如下:
A、∠3和∠5是内错角;
B、∠2和∠4无关系;
C、∠1和∠B无关系;
D、∠5和∠B是同旁内角,正确,故选D.
小试牛刀
拓展延伸
04
4.若∠α与∠β同旁内角,且∠α=50°时,则∠β的度数为( )
A.50° B.130° C.50°或130° D.无法确定
【答案】D
小试牛刀
课堂小结
05
同位角、内错角、同旁内角总结
角的 名称 角的特征 基本图形 基本图形 相同点 共同特征
同位角
同旁 内角
内错角
课堂小结
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
F
U
Z
都在截线同侧
都在被截线之间
这三类角都是没有公共顶点的.
谢谢观看!
注:本视频所有素材来源于网络,如有侵权,请联系我们。
