2021-2022学年人教版 数学八年级上册13.1.2线段的垂直平分线的性质-课堂练习 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版 数学八年级上册13.1.2线段的垂直平分线的性质-课堂练习 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 304.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 19:40:43 | ||
图片预览


文档简介
2021-2022学年初中(人教版)数学八年级上册
13.1.2线段的垂直平分线的性质-课堂练习
时间:40分钟
一、单选题
1.到三角形的三个顶点距离相等的点是( ).
A.三角形三条中线的交点 B.三角形三边垂直平分线的交点
C.三角形三条角平分线的交点 D.三角形三条高的交点
2.如图,为中边的中垂线,,则的周长是( )
A.16 B.18 C.26 D.28
3.下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是( )
A.CA=CB,DA=DB B.CA=CB,CD⊥AB
C.CA=DA,CB=DB D.CA=CB,CD平分AB
4.如图,直线与交于点O,,下列结论中正确的是( )
A. B.
C.是的垂直平分线 D.点P在的垂直平分线上
5.如图,,,点在线段的垂直平分线上,若,,则的长为( )
A. B. C. D.
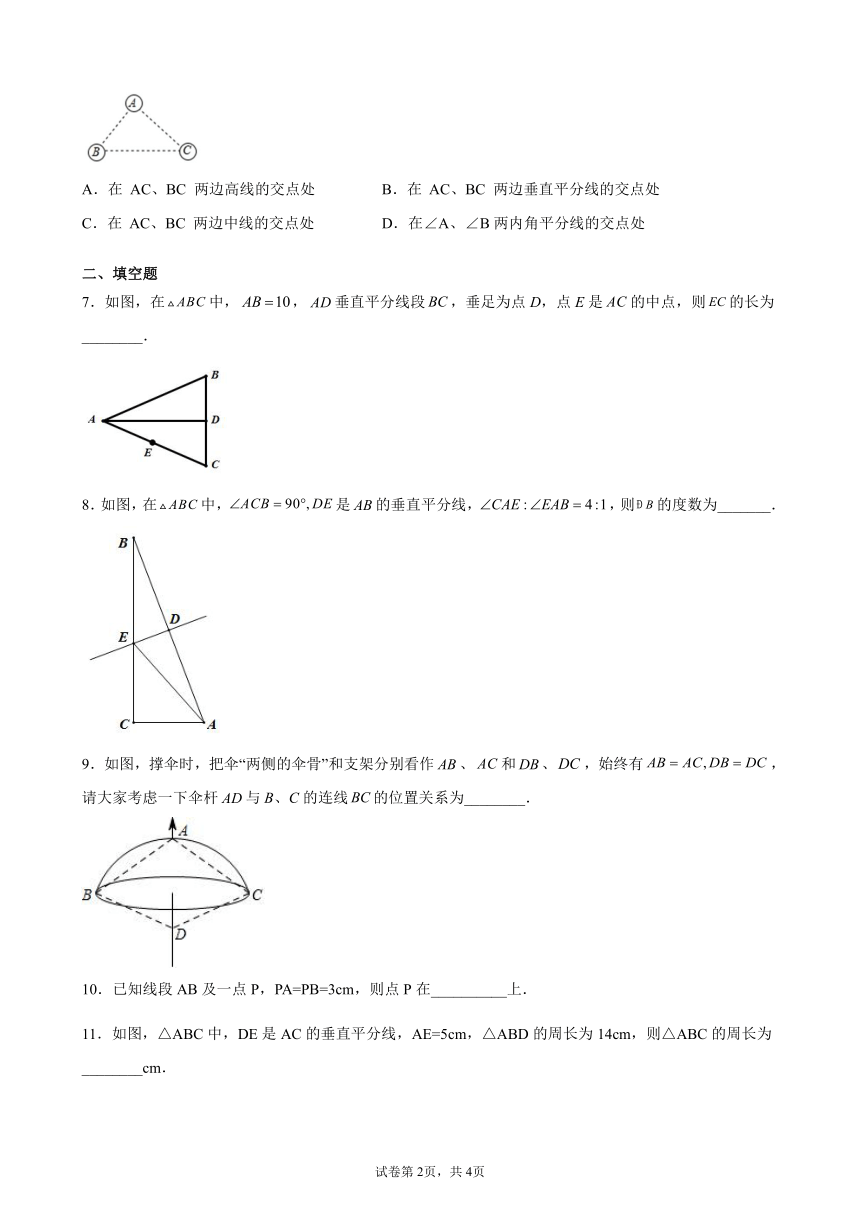
6.如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ).
A.在 AC、BC 两边高线的交点处 B.在 AC、BC 两边垂直平分线的交点处
C.在 AC、BC 两边中线的交点处 D.在∠A、∠B两内角平分线的交点处
二、填空题
7.如图,在中,,垂直平分线段,垂足为点D,点E是的中点,则的长为________.
8.如图,在中,是的垂直平分线,,则的度数为_______.
9.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
10.已知线段AB及一点P,PA=PB=3cm,则点P在__________上.
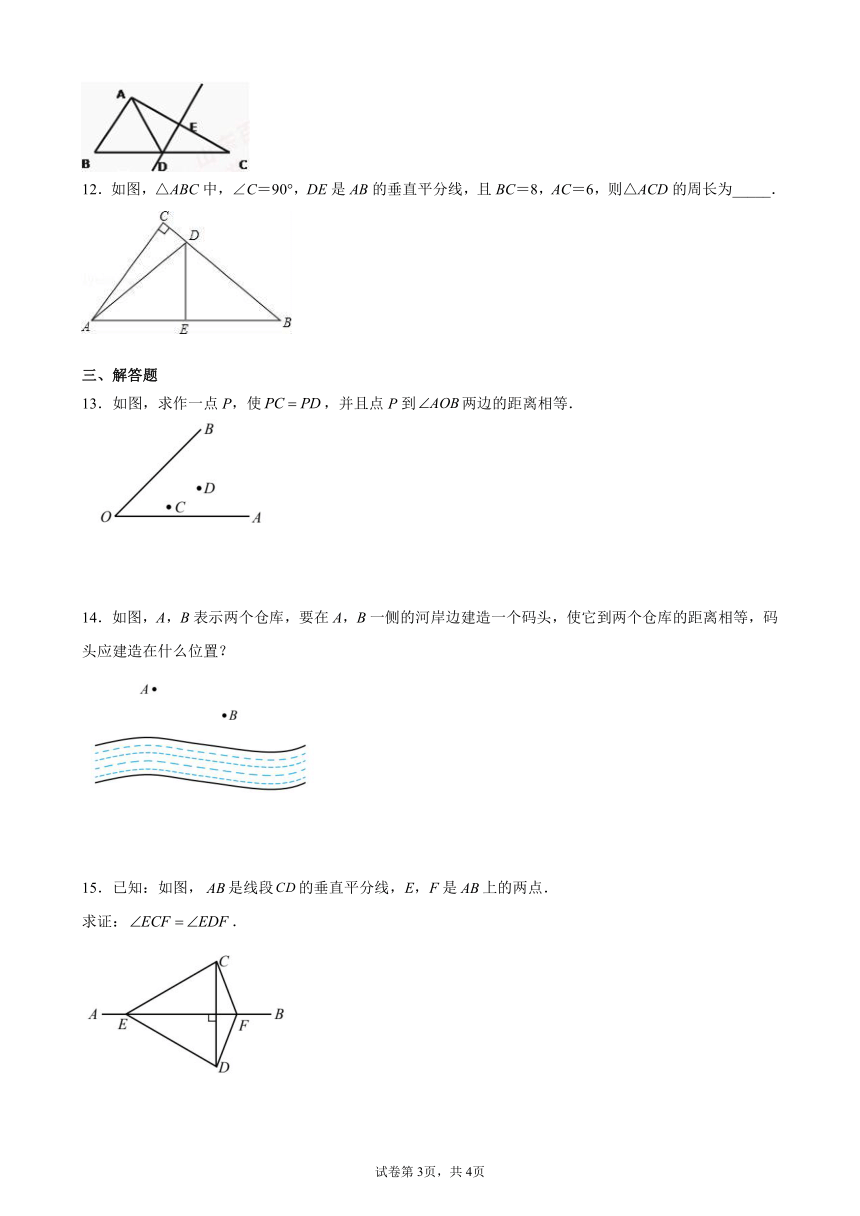
11.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为14cm,则△ABC的周长为________cm.
12.如图,△ABC中,∠C=90°,DE是AB的垂直平分线,且BC=8,AC=6,则△ACD的周长为_____.
三、解答题
13.如图,求作一点P,使,并且点P到两边的距离相等.
14.如图,A,B表示两个仓库,要在A,B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
15.已知:如图,是线段的垂直平分线,E,F是上的两点.
求证:.
16.如图,甲 乙两个单位分别位于一条封闭式街道的两旁,现准备合作修建一座过街天桥.
(1)天桥建在何处才能使由甲到乙的路线最短?注意:天桥必须与街道垂直.
(2)天桥建在何处才能使甲 乙到天桥的距离相等?
17.已知:如图,P是平分线上的一点,,垂足分别为C,D.
求证:
(1);
(2)是的垂直平分线.
18.如图,小河边有两个村庄A、B.要在河边建一自来水厂向A村与B村供水.
(1)若要使水厂到A、B村的距离相等,则应选择在哪建厂?
(2)若要使水厂到A、B村的水管最省料,应建在什么地方?(保留作图痕迹,不写作法)
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.B
【解析】解: 线段的垂直平分线上的点到线段的两个端点的距离相等,
到三角形的三个顶点距离相等的点是三角形三边的垂直平分线的交点.
故选:B
2.B
【解析】∵是中边的垂直平分线,∴,
∴,
∴的周长.
故选:B.
3.C
【解析】解:A、CA=CB,DA=DB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意;
B、CA=CB,CD⊥AB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意;
C、CA=DA,CB=DB,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,符合题意;
D、CA=CB,CD平分AB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意.
故选:C.
4.D
【解析】解:因为直线PO与AB交于点O,且PA=PB,
所以P在线段AB的垂直平分线上,
故选:D.
5.C
【解析】解:,,
,
点在线段的垂直平分线上,
,
,
故选:.
6.B
【解析】解:根据线段垂直平分线上的点到线段两个端点的距离相等,
可知超市应建在AC、BC两边垂直平分线的交点处,
故选:B.
7.5
【解析】∵垂直平分,,
∴,
∵点E是的中点,
∴.
故答案为:5.
8.15°
【解析】解:∵在Rt△ABC中,,
∵DE是AB的垂直平分线
∴∠B=∠BAE
∵∠CAE:∠EAB=4:1
∴6∠B=90°
∴∠B=15°
故答案为:15°.
9.垂直
【解析】解:如图,连接、,
∵,
∴点A在线段的垂直平分线上,点D在线段的垂直平分线上,
∴根据两点确定一条直线得出直线是线段的垂直平分线,
故答案为:垂直.
10.线段AB的垂直平分线
【解析】因为PA=PB=3cm,
所以P点一定在线段AB的垂直平分线上.
故答案为:线段AB的垂直平分线.
11.24
【解析】∵DE是AC的垂直平分线
∴AD=CD,AE=EC=5cm,
∴AC=10cm
∵△ABD的周长为14cm
∴AB+BD+AD=14,
△ABC的周长为AB+BC+AC= AB+ BD+ CD+AC= AB+BD+AD+AC=14+10=24cm.
12.14.
【解析】∵DE是AB的垂直平分线,∴DA=DB,∴△ACD的周长=AC+CD+AD=AC+CD+DB=AC+BC=14.
故答案为14.
13.图见解析
【解析】解:如下图所示,点P就是所求的点.
14.见解析.
【解析】解:连接AB,分别以A和B为圆心,以大于为半径的两弧交于点E和F,
作直线EF,与河岸交于点C,如图,则码头应建在点C处.
15.证明见解析
【解析】证明:是线段的垂直平分线,E,F是上的两点,
,
又,
(SSS),
.
16.(1)见解析;(2)见解析
【解析】解:(1)如图(1),将点A沿竖直向下的方向平移,平移距离等于桥长,到达点,连接,与街道靠近B的一侧交于点,过点建桥即符合要求;
(2)如图(2),作点B关于街道的对称点,连接,作的垂直平分线,与街道靠近A的一侧相交于点,过点建桥即符合要求.
17.(1)证明见解析;(2)证明见解析.
【解析】解:(1)证明:∵P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,
∴PC=PD,
在Rt△POC与Rt△POD中,
∵,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD;
(2)证明:∵P是∠AOB平分线上的一点,
∴∠COP=∠DOP
∵由(1)知,OC=OD,
∴在△COE与△DOE中,
,
∴△COE≌△DOE,
∴CE=DE,OE⊥CD,即OP是CD的垂直平分线.
18.(1)答案见解析;(2)答案见解析.
【解析】解:(1)作出AB的中垂线与EF的交点M,交点M即为厂址所在位置;
(2)如图所示:作A点关于直线EF的对称点A′,再连接A′B交EF于点N,点N即为所求.
答案第1页,共2页
答案第1页,共2页
13.1.2线段的垂直平分线的性质-课堂练习
时间:40分钟
一、单选题
1.到三角形的三个顶点距离相等的点是( ).
A.三角形三条中线的交点 B.三角形三边垂直平分线的交点
C.三角形三条角平分线的交点 D.三角形三条高的交点
2.如图,为中边的中垂线,,则的周长是( )
A.16 B.18 C.26 D.28
3.下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是( )
A.CA=CB,DA=DB B.CA=CB,CD⊥AB
C.CA=DA,CB=DB D.CA=CB,CD平分AB
4.如图,直线与交于点O,,下列结论中正确的是( )
A. B.
C.是的垂直平分线 D.点P在的垂直平分线上
5.如图,,,点在线段的垂直平分线上,若,,则的长为( )
A. B. C. D.
6.如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ).
A.在 AC、BC 两边高线的交点处 B.在 AC、BC 两边垂直平分线的交点处
C.在 AC、BC 两边中线的交点处 D.在∠A、∠B两内角平分线的交点处
二、填空题
7.如图,在中,,垂直平分线段,垂足为点D,点E是的中点,则的长为________.
8.如图,在中,是的垂直平分线,,则的度数为_______.
9.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作、和、,始终有,请大家考虑一下伞杆与B、C的连线的位置关系为________.
10.已知线段AB及一点P,PA=PB=3cm,则点P在__________上.
11.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为14cm,则△ABC的周长为________cm.
12.如图,△ABC中,∠C=90°,DE是AB的垂直平分线,且BC=8,AC=6,则△ACD的周长为_____.
三、解答题
13.如图,求作一点P,使,并且点P到两边的距离相等.
14.如图,A,B表示两个仓库,要在A,B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建造在什么位置?
15.已知:如图,是线段的垂直平分线,E,F是上的两点.
求证:.
16.如图,甲 乙两个单位分别位于一条封闭式街道的两旁,现准备合作修建一座过街天桥.
(1)天桥建在何处才能使由甲到乙的路线最短?注意:天桥必须与街道垂直.
(2)天桥建在何处才能使甲 乙到天桥的距离相等?
17.已知:如图,P是平分线上的一点,,垂足分别为C,D.
求证:
(1);
(2)是的垂直平分线.
18.如图,小河边有两个村庄A、B.要在河边建一自来水厂向A村与B村供水.
(1)若要使水厂到A、B村的距离相等,则应选择在哪建厂?
(2)若要使水厂到A、B村的水管最省料,应建在什么地方?(保留作图痕迹,不写作法)
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.B
【解析】解: 线段的垂直平分线上的点到线段的两个端点的距离相等,
到三角形的三个顶点距离相等的点是三角形三边的垂直平分线的交点.
故选:B
2.B
【解析】∵是中边的垂直平分线,∴,
∴,
∴的周长.
故选:B.
3.C
【解析】解:A、CA=CB,DA=DB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意;
B、CA=CB,CD⊥AB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意;
C、CA=DA,CB=DB,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,符合题意;
D、CA=CB,CD平分AB,可以判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线,不符合题意.
故选:C.
4.D
【解析】解:因为直线PO与AB交于点O,且PA=PB,
所以P在线段AB的垂直平分线上,
故选:D.
5.C
【解析】解:,,
,
点在线段的垂直平分线上,
,
,
故选:.
6.B
【解析】解:根据线段垂直平分线上的点到线段两个端点的距离相等,
可知超市应建在AC、BC两边垂直平分线的交点处,
故选:B.
7.5
【解析】∵垂直平分,,
∴,
∵点E是的中点,
∴.
故答案为:5.
8.15°
【解析】解:∵在Rt△ABC中,,
∵DE是AB的垂直平分线
∴∠B=∠BAE
∵∠CAE:∠EAB=4:1
∴6∠B=90°
∴∠B=15°
故答案为:15°.
9.垂直
【解析】解:如图,连接、,
∵,
∴点A在线段的垂直平分线上,点D在线段的垂直平分线上,
∴根据两点确定一条直线得出直线是线段的垂直平分线,
故答案为:垂直.
10.线段AB的垂直平分线
【解析】因为PA=PB=3cm,
所以P点一定在线段AB的垂直平分线上.
故答案为:线段AB的垂直平分线.
11.24
【解析】∵DE是AC的垂直平分线
∴AD=CD,AE=EC=5cm,
∴AC=10cm
∵△ABD的周长为14cm
∴AB+BD+AD=14,
△ABC的周长为AB+BC+AC= AB+ BD+ CD+AC= AB+BD+AD+AC=14+10=24cm.
12.14.
【解析】∵DE是AB的垂直平分线,∴DA=DB,∴△ACD的周长=AC+CD+AD=AC+CD+DB=AC+BC=14.
故答案为14.
13.图见解析
【解析】解:如下图所示,点P就是所求的点.
14.见解析.
【解析】解:连接AB,分别以A和B为圆心,以大于为半径的两弧交于点E和F,
作直线EF,与河岸交于点C,如图,则码头应建在点C处.
15.证明见解析
【解析】证明:是线段的垂直平分线,E,F是上的两点,
,
又,
(SSS),
.
16.(1)见解析;(2)见解析
【解析】解:(1)如图(1),将点A沿竖直向下的方向平移,平移距离等于桥长,到达点,连接,与街道靠近B的一侧交于点,过点建桥即符合要求;
(2)如图(2),作点B关于街道的对称点,连接,作的垂直平分线,与街道靠近A的一侧相交于点,过点建桥即符合要求.
17.(1)证明见解析;(2)证明见解析.
【解析】解:(1)证明:∵P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,
∴PC=PD,
在Rt△POC与Rt△POD中,
∵,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD;
(2)证明:∵P是∠AOB平分线上的一点,
∴∠COP=∠DOP
∵由(1)知,OC=OD,
∴在△COE与△DOE中,
,
∴△COE≌△DOE,
∴CE=DE,OE⊥CD,即OP是CD的垂直平分线.
18.(1)答案见解析;(2)答案见解析.
【解析】解:(1)作出AB的中垂线与EF的交点M,交点M即为厂址所在位置;
(2)如图所示:作A点关于直线EF的对称点A′,再连接A′B交EF于点N,点N即为所求.
答案第1页,共2页
答案第1页,共2页
