人教版 2021-2022学年数学八年级上册14.2.1平方差公式课堂专练习题(word版、含答案)
文档属性
| 名称 | 人教版 2021-2022学年数学八年级上册14.2.1平方差公式课堂专练习题(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 225.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 20:58:13 | ||
图片预览


文档简介
2021-2022学年初中(人教版)数学八年级上册
14.2.1平方差公式-课堂专练
时间:40分钟
一、单选题
1.如图,从边长为的大正方形纸片中挖去一个边长为的小正方形纸片后,将其裁成四个相同的等腰梯形(甲),然后拼成一个平行四边形(乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式是( )
A. B.
C. D.
2.下面计算正确的是( )
A.原式
B.原式
C.原式
D.原式
3.的计算结果是( )
A. B. C. D.
4.若,则的值为( )
A. B. C.1 D.2
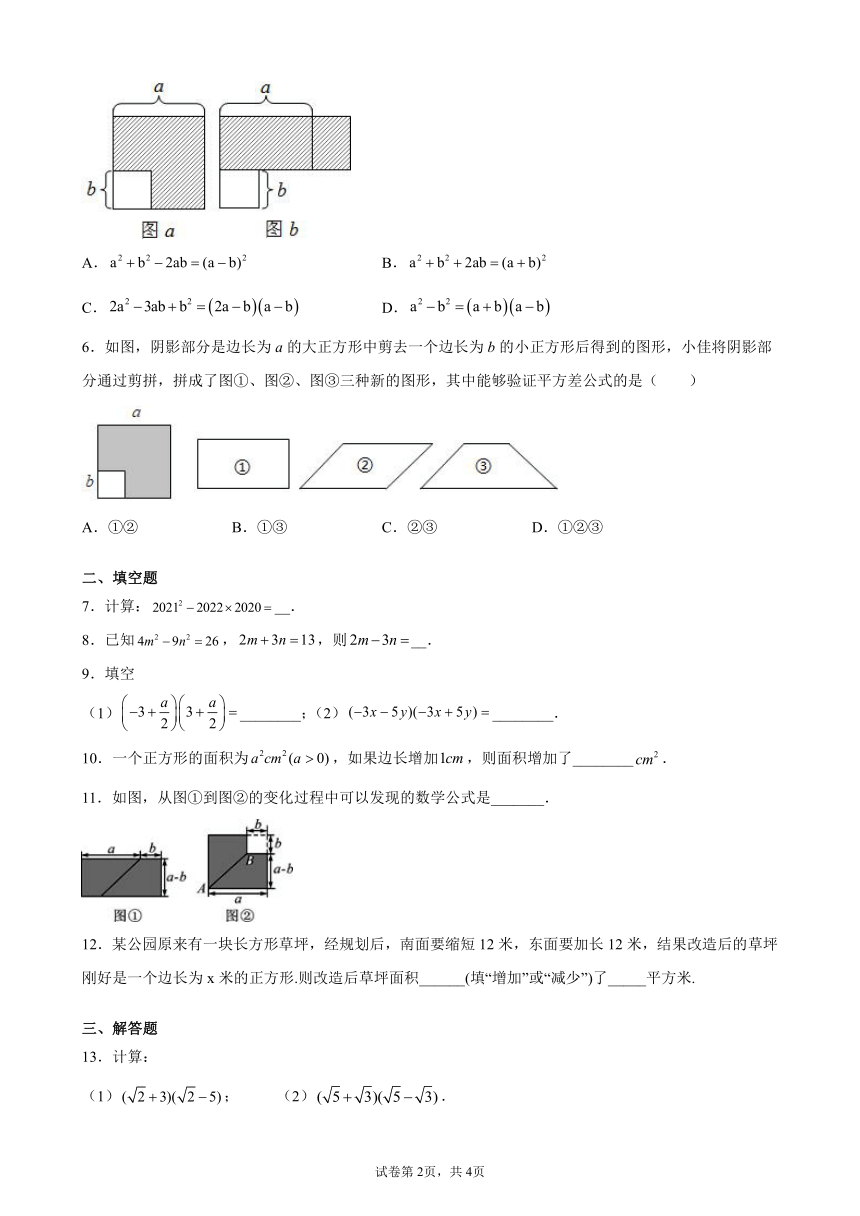
5.如图所示,从边长为a的大正方形中挖去一个边长是b的小正方形,小明将图a中的阴影部分拼成了一个如图b所示的矩形,这一过程可以验证
A. B.
C. D.
6.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后得到的图形,小佳将阴影部分通过剪拼,拼成了图①、图②、图③三种新的图形,其中能够验证平方差公式的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
7.计算:__.
8.已知,,则__.
9.填空
(1)________;(2)________.
10.一个正方形的面积为,如果边长增加,则面积增加了________.
11.如图,从图①到图②的变化过程中可以发现的数学公式是_______.
12.某公园原来有一块长方形草坪,经规划后,南面要缩短12米,东面要加长12米,结果改造后的草坪刚好是一个边长为x米的正方形.则改造后草坪面积______(填“增加”或“减少”)了_____平方米.
三、解答题
13.计算:
(1); (2).
14.下面各式的计算对不对?如果不对,应当怎样改正?
(1);(2).
15.运用平方差公式计算:
(1);(2);(3)
(4);(5);(6).
16.如图,将边长为m的正方形纸板沿虚线剪成两个小正方形和两个矩形,拿掉边长为n的小正方形纸板后,将剩下的三块拼成新的矩形.
(1)用含m或n的代数式表示拼成矩形的周长;
(2)m=7,n=4,求拼成矩形的面积.
17.如图,王大妈家有一块边长为的正方形土地租给了邻居李大爷种植,今年,他对李大爷说:“我把你这块地的一边减少,另一边增加,继续租给你,你也没有吃亏,你看如何”.李大爷一听,就答应了.同学们,你认为李大爷吃亏了吗?为什么?
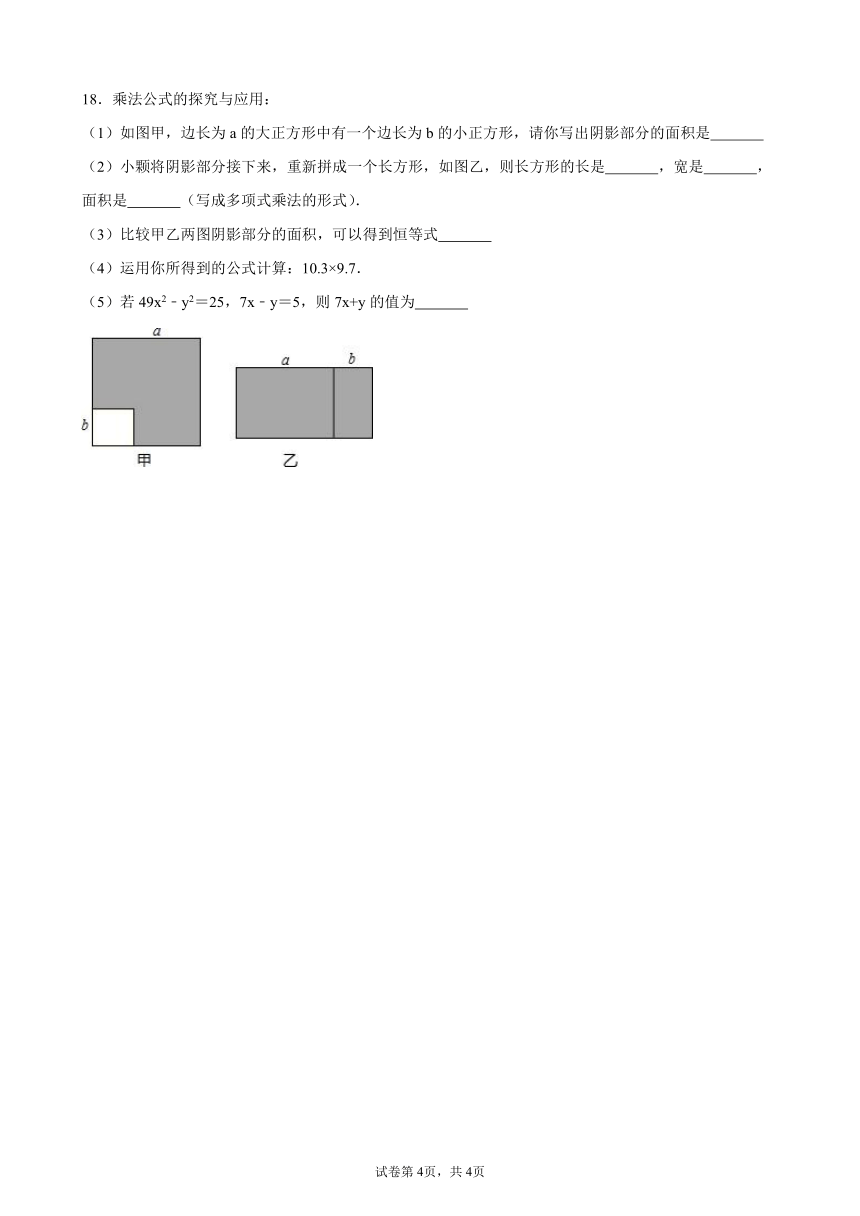
18.乘法公式的探究与应用:
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分的面积是
(2)小颗将阴影部分接下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到恒等式
(4)运用你所得到的公式计算:10.3×9.7.
(5)若49x2﹣y2=25,7x﹣y=5,则7x+y的值为
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:图甲中阴影部分的面积为:a2-b2,图乙中阴影部分的面积为:(a+b)(a-b)
∵甲乙两图中阴影部分的面积相等
∴a2-b2=(a+b)(a-b)
∴可以验证成立的公式为(a+b)(a-b)=a2-b2.
故选:D.
2.C
【解析】
故选C.
3.C
【解析】.
故选C
4.B
【解析】解:∵,
∴=====.
故选B.
5.D
【解析】由题可知a2-b2=(a+b)(a-b).
故选D.
6.D
【解析】解:(1)如图①,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的长为(a+b),宽为(a-b)的长方形,因此面积为(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以①符合题意;
(2)如图②,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的底为(a+b),高为(a-b)的平行四边形,因此面积为(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以②符合题意;
(3)如图③,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的上底为2b,下底为2a,,高为(a-b)的梯形,因此面积为(2a+2b)(a-b)=(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以③符合题意;
综上所述,①②③都符合题意,
故选:D.
7.1
【解析】解:原式
,
故答案为:1.
8.2
【解析】解:,
又,
,
,
故答案为:2.
9.
【解析】解:(1);
(2);
故答案为:;.
10.
【解析】解:∵原正方形的面积为a2cm2,
∴边长为acm,
∴增加后的边长是(a+1)cm,
∴增加的面积=(a+1)2-a2=(a+1+a)(a+1-a)=2a+1.
故答案为:(2a+1).
11.(a+b)(a-b)=a2-b2
【解析】∵图①的面积为(a+b)(a-b),图②的面积为a2-b2,
∴(a+b)(a-b)=a2-b2.
12.增加 144
【解析】由题意知,公园原来的草坪长为(x+12)米,宽为(x-12)米,
∴原来草坪面积为:(x+12)(x-12)= x2-144(平方米),
∵改造后的面积是x2平方米,
∴改造后草坪面积增加了,增加了144平方米.
故答案为:增加;144.
13.(1);(2)2.
【解析】解:(1)
;
(2)
.
14.(1)不对,应为;(2)不对,应为.
【解析】解:(1)计算错误.
正确解答为:;
(2)计算错误.
正确解答为:;
15.(1);(2);(3);(4);(5)3999999;(6)999996.
【解析】解:(1)
=
=;
(2)
(3)
(4)
(5)2001×1999
=(2000+1)×(2000 1)
=
=4000000 1
=3999999
(6)998×1002
=(1000 2)×(1000+2)
=
=1000000 4
=999996.
16.(1)矩形的周长为4m;(2)矩形的面积为33.
【解析】(1)矩形的长为:m﹣n,
矩形的宽为:m+n,
矩形的周长为:2[(m-n)+(m+n)]=4m;
(2)矩形的面积为S=(m+n)(m﹣n)=m2-n2,
当m=7,n=4时,S=72-42=33.
17.李大爷吃亏了.
【解析】李大爷吃亏了.
原来正方形地的面积,当一边减少4,另一边增加4时,面积为,
因为,
所以李大爷吃亏了.
18.(1)a2﹣b2;(2)a+b,a﹣b,(a+b)(a﹣b);(3)(a+b)(a﹣b)=a2﹣b2;(4)99.91;(5)5
【解析】解:(1)阴影部分的面积=大正方形的面积﹣小正方形的面积=a2﹣b2
故答案为:a2﹣b2.
(2)长方形的长是(a+b),宽是(a﹣b),面积=长×宽=(a+b)(a﹣b)
故答案为:a+b;a﹣b;(a+b)(a﹣b).
(3)由(1)(2)可得(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
(4)10.3×9.7
=(10+0.3)(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91
(5)∵49x2﹣y2=25,
∴(7x+y)(7x﹣y)=25
∵7x﹣y=5
∴(7x+y)×5=25
∴7x+y=5
故答案为:5.答案第1页,共2页
答案第1页,共2页
14.2.1平方差公式-课堂专练
时间:40分钟
一、单选题
1.如图,从边长为的大正方形纸片中挖去一个边长为的小正方形纸片后,将其裁成四个相同的等腰梯形(甲),然后拼成一个平行四边形(乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式是( )
A. B.
C. D.
2.下面计算正确的是( )
A.原式
B.原式
C.原式
D.原式
3.的计算结果是( )
A. B. C. D.
4.若,则的值为( )
A. B. C.1 D.2
5.如图所示,从边长为a的大正方形中挖去一个边长是b的小正方形,小明将图a中的阴影部分拼成了一个如图b所示的矩形,这一过程可以验证
A. B.
C. D.
6.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后得到的图形,小佳将阴影部分通过剪拼,拼成了图①、图②、图③三种新的图形,其中能够验证平方差公式的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
7.计算:__.
8.已知,,则__.
9.填空
(1)________;(2)________.
10.一个正方形的面积为,如果边长增加,则面积增加了________.
11.如图,从图①到图②的变化过程中可以发现的数学公式是_______.
12.某公园原来有一块长方形草坪,经规划后,南面要缩短12米,东面要加长12米,结果改造后的草坪刚好是一个边长为x米的正方形.则改造后草坪面积______(填“增加”或“减少”)了_____平方米.
三、解答题
13.计算:
(1); (2).
14.下面各式的计算对不对?如果不对,应当怎样改正?
(1);(2).
15.运用平方差公式计算:
(1);(2);(3)
(4);(5);(6).
16.如图,将边长为m的正方形纸板沿虚线剪成两个小正方形和两个矩形,拿掉边长为n的小正方形纸板后,将剩下的三块拼成新的矩形.
(1)用含m或n的代数式表示拼成矩形的周长;
(2)m=7,n=4,求拼成矩形的面积.
17.如图,王大妈家有一块边长为的正方形土地租给了邻居李大爷种植,今年,他对李大爷说:“我把你这块地的一边减少,另一边增加,继续租给你,你也没有吃亏,你看如何”.李大爷一听,就答应了.同学们,你认为李大爷吃亏了吗?为什么?
18.乘法公式的探究与应用:
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分的面积是
(2)小颗将阴影部分接下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到恒等式
(4)运用你所得到的公式计算:10.3×9.7.
(5)若49x2﹣y2=25,7x﹣y=5,则7x+y的值为
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:图甲中阴影部分的面积为:a2-b2,图乙中阴影部分的面积为:(a+b)(a-b)
∵甲乙两图中阴影部分的面积相等
∴a2-b2=(a+b)(a-b)
∴可以验证成立的公式为(a+b)(a-b)=a2-b2.
故选:D.
2.C
【解析】
故选C.
3.C
【解析】.
故选C
4.B
【解析】解:∵,
∴=====.
故选B.
5.D
【解析】由题可知a2-b2=(a+b)(a-b).
故选D.
6.D
【解析】解:(1)如图①,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的长为(a+b),宽为(a-b)的长方形,因此面积为(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以①符合题意;
(2)如图②,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的底为(a+b),高为(a-b)的平行四边形,因此面积为(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以②符合题意;
(3)如图③,
左图的阴影部分的面积为a2-b2,裁剪后拼接成右图的上底为2b,下底为2a,,高为(a-b)的梯形,因此面积为(2a+2b)(a-b)=(a+b)(a-b),
因此有a2-b2=(a+b)(a-b),
所以③符合题意;
综上所述,①②③都符合题意,
故选:D.
7.1
【解析】解:原式
,
故答案为:1.
8.2
【解析】解:,
又,
,
,
故答案为:2.
9.
【解析】解:(1);
(2);
故答案为:;.
10.
【解析】解:∵原正方形的面积为a2cm2,
∴边长为acm,
∴增加后的边长是(a+1)cm,
∴增加的面积=(a+1)2-a2=(a+1+a)(a+1-a)=2a+1.
故答案为:(2a+1).
11.(a+b)(a-b)=a2-b2
【解析】∵图①的面积为(a+b)(a-b),图②的面积为a2-b2,
∴(a+b)(a-b)=a2-b2.
12.增加 144
【解析】由题意知,公园原来的草坪长为(x+12)米,宽为(x-12)米,
∴原来草坪面积为:(x+12)(x-12)= x2-144(平方米),
∵改造后的面积是x2平方米,
∴改造后草坪面积增加了,增加了144平方米.
故答案为:增加;144.
13.(1);(2)2.
【解析】解:(1)
;
(2)
.
14.(1)不对,应为;(2)不对,应为.
【解析】解:(1)计算错误.
正确解答为:;
(2)计算错误.
正确解答为:;
15.(1);(2);(3);(4);(5)3999999;(6)999996.
【解析】解:(1)
=
=;
(2)
(3)
(4)
(5)2001×1999
=(2000+1)×(2000 1)
=
=4000000 1
=3999999
(6)998×1002
=(1000 2)×(1000+2)
=
=1000000 4
=999996.
16.(1)矩形的周长为4m;(2)矩形的面积为33.
【解析】(1)矩形的长为:m﹣n,
矩形的宽为:m+n,
矩形的周长为:2[(m-n)+(m+n)]=4m;
(2)矩形的面积为S=(m+n)(m﹣n)=m2-n2,
当m=7,n=4时,S=72-42=33.
17.李大爷吃亏了.
【解析】李大爷吃亏了.
原来正方形地的面积,当一边减少4,另一边增加4时,面积为,
因为,
所以李大爷吃亏了.
18.(1)a2﹣b2;(2)a+b,a﹣b,(a+b)(a﹣b);(3)(a+b)(a﹣b)=a2﹣b2;(4)99.91;(5)5
【解析】解:(1)阴影部分的面积=大正方形的面积﹣小正方形的面积=a2﹣b2
故答案为:a2﹣b2.
(2)长方形的长是(a+b),宽是(a﹣b),面积=长×宽=(a+b)(a﹣b)
故答案为:a+b;a﹣b;(a+b)(a﹣b).
(3)由(1)(2)可得(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
(4)10.3×9.7
=(10+0.3)(10﹣0.3)
=102﹣0.32
=100﹣0.09
=99.91
(5)∵49x2﹣y2=25,
∴(7x+y)(7x﹣y)=25
∵7x﹣y=5
∴(7x+y)×5=25
∴7x+y=5
故答案为:5.答案第1页,共2页
答案第1页,共2页
