5.2.2 《平行线的判定》 教学课件(共30张PPT)
文档属性
| 名称 | 5.2.2 《平行线的判定》 教学课件(共30张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 21.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
人教版数学 七年级下册
5.2.2平行线的判定
学习目标
01
掌握平行线的三种判定方法,并初步运用它们进行简单的推理论证。
经历判定直线平行方法的探究过程,初步学会简单的论证和推理。
初步了解转化的数学思想方法。
学习目标
知识回顾
02
平行线的知识点回顾
同一平面内,不相交的两条直线叫做平行线。
a
b
平行用符号“∥”表示,如直线a与直线b平行,
记作:a∥b,读作“a平行于b”。
注意:平行线是相互的,如直线a与直线b平行,
记作:a∥b,也可写成b∥a。
平行线的概念:
表示方法:
知识回顾
平行线的知识点回顾
平行线的性质(平行公理):
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
a
b
c
几何语言表达式:
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论:
∵ a∥n, m∥n (已知)
∴ a∥m (平行线的传递性)
知识回顾
新课教学
03
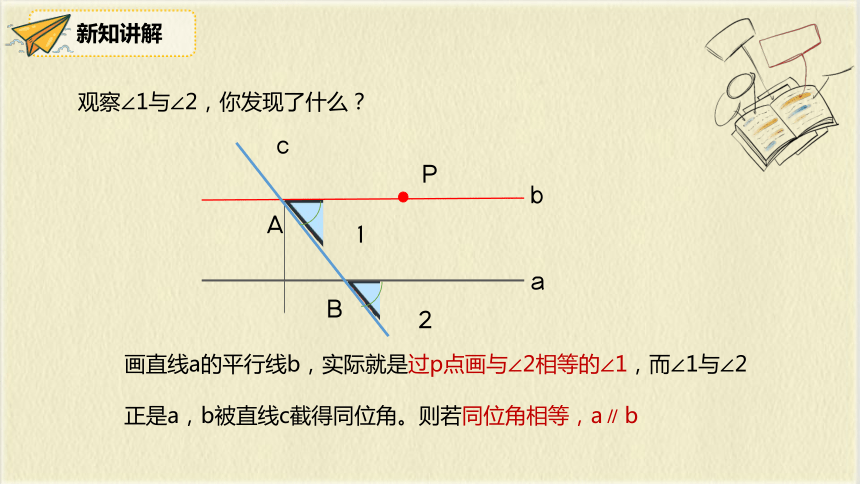
回顾画平行线的知识点
给一条直线a,你能画出直线a的平行线吗?
a
b
平行线的画法 :一放、二靠、三推、四画。
P
新课引入
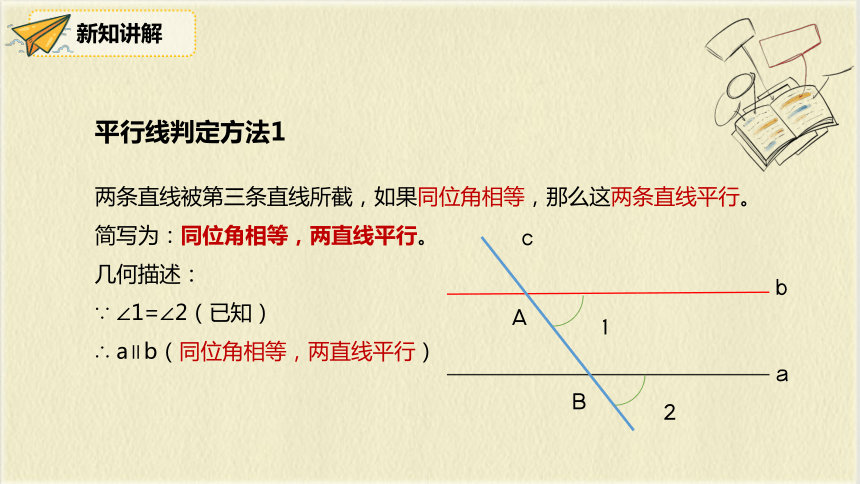
画直线a的平行线b,实际就是过p点画与∠2相等的∠1,而∠1与∠2正是a,b被直线c截得同位角。则若同位角相等,a∥ b
观察∠1与∠2,你发现了什么?
a
b
c
1
2
A
B
P
新知讲解
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简写为:同位角相等,两直线平行。
几何描述:
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
平行线判定方法1
a
b
c
1
2
A
B
新知讲解
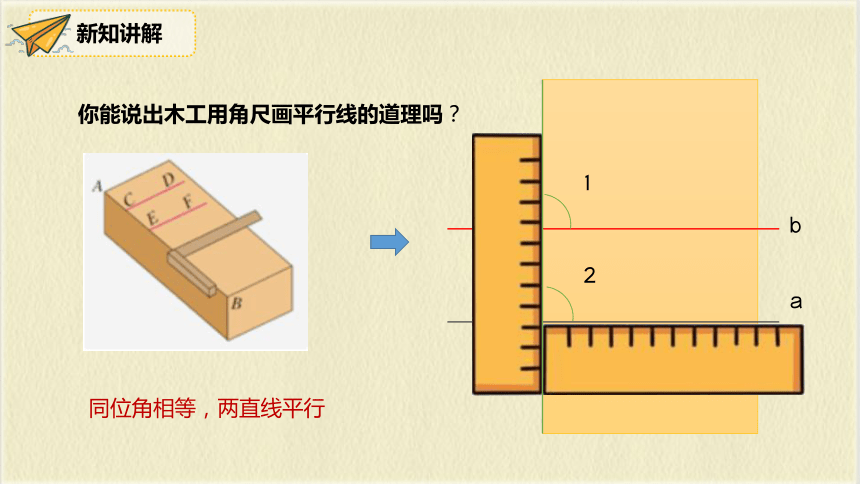
你能说出木工用角尺画平行线的道理吗?
a
b
1
2
同位角相等,两直线平行
新知讲解
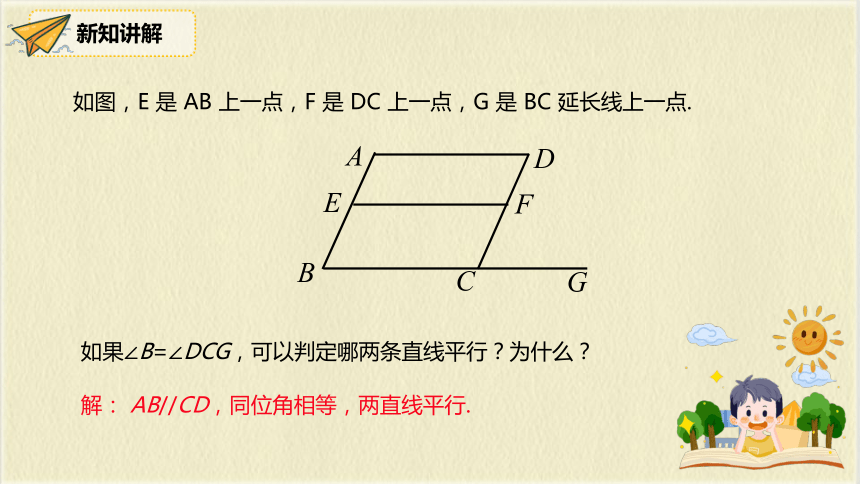
如图,E 是 AB 上一点,F 是 DC 上一点,G 是 BC 延长线上一点.
如果∠B=∠DCG,可以判定哪两条直线平行?为什么?
A
B
D
C
E
F
G
解: AB//CD,同位角相等,两直线平行.
新知讲解
a
b
c
1
2
A
B
3
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢
∵ ∠1=∠3
而∠2=∠3 (对顶角相等)
∴ ∠2=∠1(等量代换)
∴ a ∥ b(同位角相等,两直线平行)
如图,已知∠1=∠3,试说明a ∥ b.
新知讲解
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简写为:内错角相等,两直线平行。
几何描述:
∵ ∠1=∠2(已知)
∴ a ∥ b(内错角相等,两直线平行)
a
b
c
1
A
B
2
新知讲解
平行线判定方法2
如图,E 是 AB 上一点,F 是 DC 上一点,G 是 BC 延长线上一点.
如果∠D=∠DCG,可以判定哪两条直线平行? 为什么?
解:AD //BC,内错角相等,两直线平行.
A
B
D
C
E
F
G
新知讲解
a
b
c
1
2
A
B
3
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢 (利用内错角知识证明)
∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(内错角相等,两直线平行)
如图,已知∠1+∠3=180°,试说明a∥b.
新知讲解
a
b
c
1
2
A
B
3
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢 (利用同位角知识证明)
∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1+∠3=180°,试说明a∥b.
新知讲解
两条直线被第三条直线所截,如果同旁同角互补,那么这两条直线平行。
简写为:同旁内角互补,两直线平行。
几何描述:
∵ ∠1+∠2=180°(已知)
∴ a∥b(同旁内角互补,两直线平行)
a
b
c
1
A
B
2
新知讲解
平行线判定方法3
如图,E 是 AB 上一点,F 是 DC 上一点,G 是 BC 延长线上一点.
如果∠D+∠DFE=180°,可以判定哪两条直线平行?为什么?
解: AD//EF,同旁内角互补,两直线平行.
A
B
D
C
E
F
G
新知讲解
小试牛刀
04
1.已知,如图.AD∥BE,∠1=∠2,求证:∠A=∠E.请完成解答过程.
证明:∵AD∥BE(已知)
∴∠A=∠ ( )
又∵∠1=∠2(已知)
∴AC∥ ( )
∴∠3=∠ (两直线平行,内错角相等)
∴∠A=∠E(等量代换)
E
3
两直线平行,同位角相等
DE
内错角相等,两直线平行
小试牛刀
2.如图,直线L1,L2分别与另两条直线相交,已知
,,若,试求∠4的大小.
【详解】
解:设∠1、∠2对顶角为∠5、∠6,
∠5+∠6=∠1+∠2=180°,
∵∠3、∠4为同旁内错角,
∴直线l1∥直线l2 ,
又∵直线l1∥直线l2
∴∠3+∠4=180°,
∴∠4=70°.
小试牛刀
3.如图,已知∠1=∠2 求证:a ∥ b.
【详解】
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴a ∥ b.
小试牛刀
4.如图,AC和BD相交于点O,OA=OC,OB=OD,则线段AB与CD有什么位置关系?并说明理由。
【详解】
在ΔABO和ΔCDO中,
AO=CO,
∠AOB=∠COD(对顶角相等),
BO=DO
∴ΔABO≌ΔCDO(SAS)
∴∠C=∠A,
则AB∥CD(内错角相等,两直线平行)
小试牛刀
5.如图,已知 ∠1=75° ,∠2 =105°. AB 与 CD 平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
解:AB//CD,理由如下:
∵ ∠1+∠3=180°,(邻补角的性质)
∠1=75°,(已知)
∴ ∠3=180°-∠1=180°-75°=105°.
∵ ∠2=105°,(已知)
∴ ∠2=∠3,(等量代换)
∴ AB//CD.(同位角相等,两直线平行)
还有其他解法吗?
小试牛刀
A
C
1
4
2
3
B
D
5
F
E
解:∵ ∠2=∠5,(对顶角相等)
∠2=105°,(已知)
∴ ∠5=105°. (等量代换)
∵ ∠1=75°,(已知)
∴ ∠1+∠5=180°,
∴ AB//CD.(同旁内角互补,两直线平行)
除了以上两种解法,还有其他解法吗?
小试牛刀
A
C
1
4
2
3
B
D
5
F
E
解:∵ ∠2+∠4=180°,(邻补角的概念)
∠2=105°,(已知)
∴ ∠4=180°-105°=75°.
∵ ∠1=75°,(已知)
∴ ∠1=∠4,
∴ AB//CD.(内错角相等,两直线平行)
小试牛刀
课堂小结
05
课堂小结
平行线判定方法1:
平行线判定方法2:
平行线判定方法3:
同位角相等,两直线平行.
内错角相等, 两直线平行.
同旁内角互补, 两直线平行.
谢谢观看!
注:本视频所有素材来源于网络,如有侵权,请联系我们。
人教版数学 七年级下册
5.2.2平行线的判定
学习目标
01
掌握平行线的三种判定方法,并初步运用它们进行简单的推理论证。
经历判定直线平行方法的探究过程,初步学会简单的论证和推理。
初步了解转化的数学思想方法。
学习目标
知识回顾
02
平行线的知识点回顾
同一平面内,不相交的两条直线叫做平行线。
a
b
平行用符号“∥”表示,如直线a与直线b平行,
记作:a∥b,读作“a平行于b”。
注意:平行线是相互的,如直线a与直线b平行,
记作:a∥b,也可写成b∥a。
平行线的概念:
表示方法:
知识回顾
平行线的知识点回顾
平行线的性质(平行公理):
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
a
b
c
几何语言表达式:
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论:
∵ a∥n, m∥n (已知)
∴ a∥m (平行线的传递性)
知识回顾
新课教学
03
回顾画平行线的知识点
给一条直线a,你能画出直线a的平行线吗?
a
b
平行线的画法 :一放、二靠、三推、四画。
P
新课引入
画直线a的平行线b,实际就是过p点画与∠2相等的∠1,而∠1与∠2正是a,b被直线c截得同位角。则若同位角相等,a∥ b
观察∠1与∠2,你发现了什么?
a
b
c
1
2
A
B
P
新知讲解
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简写为:同位角相等,两直线平行。
几何描述:
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
平行线判定方法1
a
b
c
1
2
A
B
新知讲解
你能说出木工用角尺画平行线的道理吗?
a
b
1
2
同位角相等,两直线平行
新知讲解
如图,E 是 AB 上一点,F 是 DC 上一点,G 是 BC 延长线上一点.
如果∠B=∠DCG,可以判定哪两条直线平行?为什么?
A
B
D
C
E
F
G
解: AB//CD,同位角相等,两直线平行.
新知讲解
a
b
c
1
2
A
B
3
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢
∵ ∠1=∠3
而∠2=∠3 (对顶角相等)
∴ ∠2=∠1(等量代换)
∴ a ∥ b(同位角相等,两直线平行)
如图,已知∠1=∠3,试说明a ∥ b.
新知讲解
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简写为:内错角相等,两直线平行。
几何描述:
∵ ∠1=∠2(已知)
∴ a ∥ b(内错角相等,两直线平行)
a
b
c
1
A
B
2
新知讲解
平行线判定方法2
如图,E 是 AB 上一点,F 是 DC 上一点,G 是 BC 延长线上一点.
如果∠D=∠DCG,可以判定哪两条直线平行? 为什么?
解:AD //BC,内错角相等,两直线平行.
A
B
D
C
E
F
G
新知讲解
a
b
c
1
2
A
B
3
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢 (利用内错角知识证明)
∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(内错角相等,两直线平行)
如图,已知∠1+∠3=180°,试说明a∥b.
新知讲解
a
b
c
1
2
A
B
3
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢 (利用同位角知识证明)
∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1+∠3=180°,试说明a∥b.
新知讲解
两条直线被第三条直线所截,如果同旁同角互补,那么这两条直线平行。
简写为:同旁内角互补,两直线平行。
几何描述:
∵ ∠1+∠2=180°(已知)
∴ a∥b(同旁内角互补,两直线平行)
a
b
c
1
A
B
2
新知讲解
平行线判定方法3
如图,E 是 AB 上一点,F 是 DC 上一点,G 是 BC 延长线上一点.
如果∠D+∠DFE=180°,可以判定哪两条直线平行?为什么?
解: AD//EF,同旁内角互补,两直线平行.
A
B
D
C
E
F
G
新知讲解
小试牛刀
04
1.已知,如图.AD∥BE,∠1=∠2,求证:∠A=∠E.请完成解答过程.
证明:∵AD∥BE(已知)
∴∠A=∠ ( )
又∵∠1=∠2(已知)
∴AC∥ ( )
∴∠3=∠ (两直线平行,内错角相等)
∴∠A=∠E(等量代换)
E
3
两直线平行,同位角相等
DE
内错角相等,两直线平行
小试牛刀
2.如图,直线L1,L2分别与另两条直线相交,已知
,,若,试求∠4的大小.
【详解】
解:设∠1、∠2对顶角为∠5、∠6,
∠5+∠6=∠1+∠2=180°,
∵∠3、∠4为同旁内错角,
∴直线l1∥直线l2 ,
又∵直线l1∥直线l2
∴∠3+∠4=180°,
∴∠4=70°.
小试牛刀
3.如图,已知∠1=∠2 求证:a ∥ b.
【详解】
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴a ∥ b.
小试牛刀
4.如图,AC和BD相交于点O,OA=OC,OB=OD,则线段AB与CD有什么位置关系?并说明理由。
【详解】
在ΔABO和ΔCDO中,
AO=CO,
∠AOB=∠COD(对顶角相等),
BO=DO
∴ΔABO≌ΔCDO(SAS)
∴∠C=∠A,
则AB∥CD(内错角相等,两直线平行)
小试牛刀
5.如图,已知 ∠1=75° ,∠2 =105°. AB 与 CD 平行吗?为什么?
A
C
1
4
2
3
B
D
5
F
E
解:AB//CD,理由如下:
∵ ∠1+∠3=180°,(邻补角的性质)
∠1=75°,(已知)
∴ ∠3=180°-∠1=180°-75°=105°.
∵ ∠2=105°,(已知)
∴ ∠2=∠3,(等量代换)
∴ AB//CD.(同位角相等,两直线平行)
还有其他解法吗?
小试牛刀
A
C
1
4
2
3
B
D
5
F
E
解:∵ ∠2=∠5,(对顶角相等)
∠2=105°,(已知)
∴ ∠5=105°. (等量代换)
∵ ∠1=75°,(已知)
∴ ∠1+∠5=180°,
∴ AB//CD.(同旁内角互补,两直线平行)
除了以上两种解法,还有其他解法吗?
小试牛刀
A
C
1
4
2
3
B
D
5
F
E
解:∵ ∠2+∠4=180°,(邻补角的概念)
∠2=105°,(已知)
∴ ∠4=180°-105°=75°.
∵ ∠1=75°,(已知)
∴ ∠1=∠4,
∴ AB//CD.(内错角相等,两直线平行)
小试牛刀
课堂小结
05
课堂小结
平行线判定方法1:
平行线判定方法2:
平行线判定方法3:
同位角相等,两直线平行.
内错角相等, 两直线平行.
同旁内角互补, 两直线平行.
谢谢观看!
注:本视频所有素材来源于网络,如有侵权,请联系我们。
