24.1.1 图形的旋转 课件(共16张PPT)
文档属性
| 名称 | 24.1.1 图形的旋转 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 400.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第24章 圆
24.1 旋转
课时1 图形的旋转
1.了解旋转的概念并理解它的基本性质.(重点)
2.了解旋转对称图形的有关概念及特点. (难点)
学习目标
新课导入
情境导入
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
(1)都是绕着一个定点,旋转一定的角度,得到另一个图形 的变换。
(2)转动前、后的图形全等;这种转动不改变图形的形状、大小,只改变图形的位置
(1)我们如何来定义这种转动?
(2)这种转动的特性有哪些?
解:
思考
新课讲解
知识点1 旋转的概念
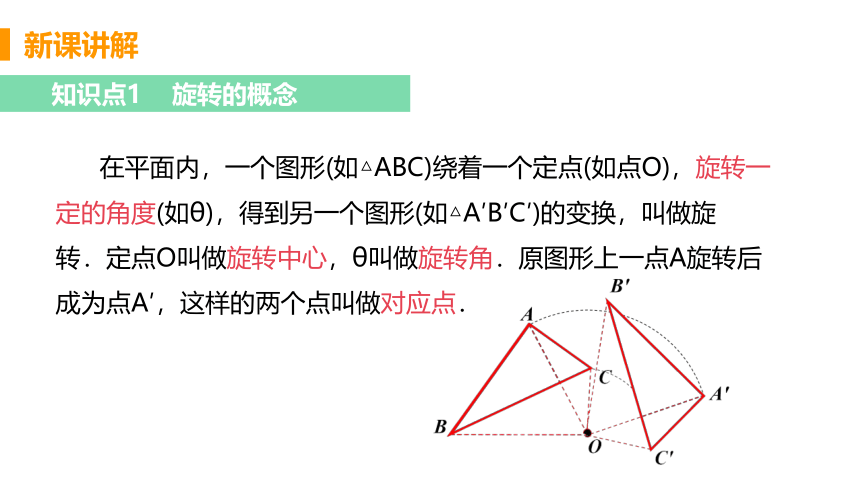
在平面内,一个图形(如△ABC)绕着一个定点(如点O),旋转一定的角度(如θ),得到另一个图形(如△A′B′C′)的变换,叫做旋转.定点O叫做旋转中心,θ叫做旋转角.原图形上一点A旋转后成为点A′,这样的两个点叫做对应点.
新课讲解
例
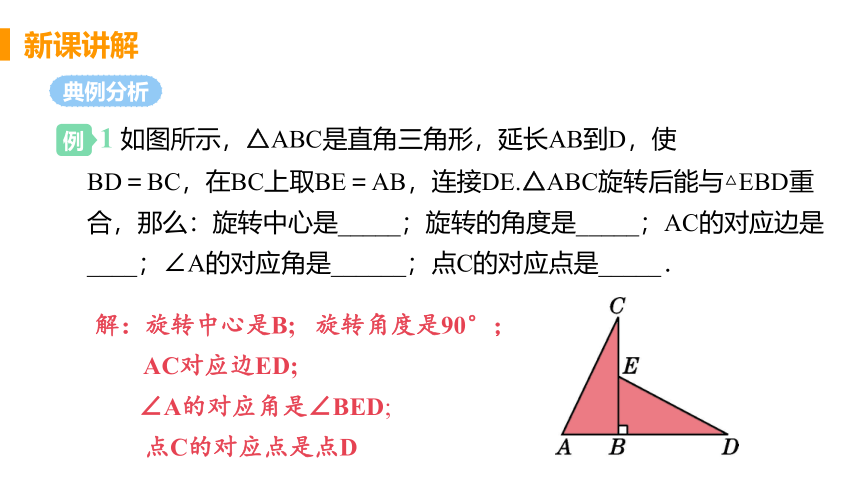
1 如图所示,△ABC是直角三角形,延长AB到D,使
BD=BC,在BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:旋转中心是_____;旋转的角度是_____;AC的对应边是____;∠A的对应角是______;点C的对应点是_____.
解:旋转中心是B; 旋转角度是90°;
AC对应边ED;
∠A的对应角是∠BED;
点C的对应点是点D
典例分析
新课讲解
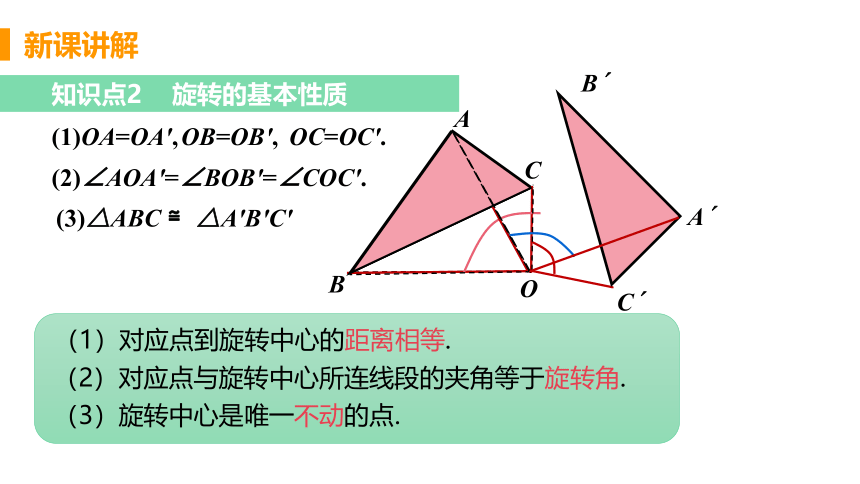
知识点2 旋转的基本性质
(3)旋转中心是唯一不动的点.
(1)对应点到旋转中心的距离相等.
(1)OA=OA′,
B
A
A
C
C
(2)对应点与旋转中心所连线段的夹角等于旋转角.
OB=OB′,
OC=OC′.
O
(3)△ABC ≌△A'B'C'
(2)∠AOA′=∠BOB′=∠COC′.
B
新课讲解
例
2如图,在正方形ABCD中,点E 在BC上,△DEC 按顺时针方向旋转一个角度后得到△DGA.
(1)图中哪一个点是旋转中心?旋转角度是多少
(2)指明图中旋转图形的对应线段与对应角.
(3)图中有除正方形的四边相等、四角相等外的相等线段与相等角吗?有没有能够完全重合的两个三角形?
若有,请各找出一对;若没有,说明理由.
典例分析
解:根据图形旋转的性质可以得到:
(1) △DEC是绕点D 顺时针旋转90°后到达△DGA位置的,
所以点D为 旋转中心,旋转角度是90°.
(2) DE与DG、DC与DA、EC与GA是对应线段, ∠CDE与 ∠ADG、∠C与∠DAG、∠DEC与∠G是对应角.
(3)有.相等线段有:DG=DE(答案不唯一);
相等角有:∠G=∠DEC(答案不唯一);
能够完全重合的两个三角形是△DEC与△DGA.
新课讲解
练一练
如图,△ABC绕点A顺时针旋转80°得到△AEF,若∠B=100°,∠F=50°,则∠α的度数是( )
A.40° B.50° C.60° D.70°
下列现象中属于旋转的有( )
①火车行驶;②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆.
A.1个 B.2个 C.3个 D.4个
1
2
D
B
新课讲解
知识点03 旋转对称图形
在平面内,一个图形绕着一个定点旋转一定的角度 θ(0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形.
新课讲解
例
3 把五角星图案,绕着它的中心点O 旋转,旋转角为多少度时,旋转后的五角星能与自身重合?
典例分析
解:
旋转角为72°或144°或216°或288°时,旋转后的五角星能与自身重合.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
当堂小练
1. 下列运动属于旋转的是( )
A.篮球的滚动 B.钟摆的摆动
C.气球升空的运动 D.一个图形沿某条直线对折的过程
2.如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,
则旋转的角度为( )
A.30°B.45°C.90°D.135°
B
B
当堂小练
3.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向
旋转45°而成的.
(1)若AB=4,则S正方形A′B′C′D′ = ;
(2) ∠BAB′= ,∠B′AD= .
(3)若连接BB′,则∠ABB′= .
16
45°
45°
67.5°
D
拓展与延伸
1.如图,将△ABC绕点A逆时针旋转得到△ADE,
点C和点E是对应点,若∠CAE=90°,AB=1,
求BD的长.
解:∵将△ABC绕点A逆时针旋转得到△ADE,
点C和点E是对应点,
∴AB=AD=1,∠BAD=∠CAE=90°,
第24章 圆
24.1 旋转
课时1 图形的旋转
1.了解旋转的概念并理解它的基本性质.(重点)
2.了解旋转对称图形的有关概念及特点. (难点)
学习目标
新课导入
情境导入
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
(1)都是绕着一个定点,旋转一定的角度,得到另一个图形 的变换。
(2)转动前、后的图形全等;这种转动不改变图形的形状、大小,只改变图形的位置
(1)我们如何来定义这种转动?
(2)这种转动的特性有哪些?
解:
思考
新课讲解
知识点1 旋转的概念
在平面内,一个图形(如△ABC)绕着一个定点(如点O),旋转一定的角度(如θ),得到另一个图形(如△A′B′C′)的变换,叫做旋转.定点O叫做旋转中心,θ叫做旋转角.原图形上一点A旋转后成为点A′,这样的两个点叫做对应点.
新课讲解
例
1 如图所示,△ABC是直角三角形,延长AB到D,使
BD=BC,在BC上取BE=AB,连接DE.△ABC旋转后能与△EBD重合,那么:旋转中心是_____;旋转的角度是_____;AC的对应边是____;∠A的对应角是______;点C的对应点是_____.
解:旋转中心是B; 旋转角度是90°;
AC对应边ED;
∠A的对应角是∠BED;
点C的对应点是点D
典例分析
新课讲解
知识点2 旋转的基本性质
(3)旋转中心是唯一不动的点.
(1)对应点到旋转中心的距离相等.
(1)OA=OA′,
B
A
A
C
C
(2)对应点与旋转中心所连线段的夹角等于旋转角.
OB=OB′,
OC=OC′.
O
(3)△ABC ≌△A'B'C'
(2)∠AOA′=∠BOB′=∠COC′.
B
新课讲解
例
2如图,在正方形ABCD中,点E 在BC上,△DEC 按顺时针方向旋转一个角度后得到△DGA.
(1)图中哪一个点是旋转中心?旋转角度是多少
(2)指明图中旋转图形的对应线段与对应角.
(3)图中有除正方形的四边相等、四角相等外的相等线段与相等角吗?有没有能够完全重合的两个三角形?
若有,请各找出一对;若没有,说明理由.
典例分析
解:根据图形旋转的性质可以得到:
(1) △DEC是绕点D 顺时针旋转90°后到达△DGA位置的,
所以点D为 旋转中心,旋转角度是90°.
(2) DE与DG、DC与DA、EC与GA是对应线段, ∠CDE与 ∠ADG、∠C与∠DAG、∠DEC与∠G是对应角.
(3)有.相等线段有:DG=DE(答案不唯一);
相等角有:∠G=∠DEC(答案不唯一);
能够完全重合的两个三角形是△DEC与△DGA.
新课讲解
练一练
如图,△ABC绕点A顺时针旋转80°得到△AEF,若∠B=100°,∠F=50°,则∠α的度数是( )
A.40° B.50° C.60° D.70°
下列现象中属于旋转的有( )
①火车行驶;②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆.
A.1个 B.2个 C.3个 D.4个
1
2
D
B
新课讲解
知识点03 旋转对称图形
在平面内,一个图形绕着一个定点旋转一定的角度 θ(0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形.
新课讲解
例
3 把五角星图案,绕着它的中心点O 旋转,旋转角为多少度时,旋转后的五角星能与自身重合?
典例分析
解:
旋转角为72°或144°或216°或288°时,旋转后的五角星能与自身重合.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
当堂小练
1. 下列运动属于旋转的是( )
A.篮球的滚动 B.钟摆的摆动
C.气球升空的运动 D.一个图形沿某条直线对折的过程
2.如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,
则旋转的角度为( )
A.30°B.45°C.90°D.135°
B
B
当堂小练
3.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向
旋转45°而成的.
(1)若AB=4,则S正方形A′B′C′D′ = ;
(2) ∠BAB′= ,∠B′AD= .
(3)若连接BB′,则∠ABB′= .
16
45°
45°
67.5°
D
拓展与延伸
1.如图,将△ABC绕点A逆时针旋转得到△ADE,
点C和点E是对应点,若∠CAE=90°,AB=1,
求BD的长.
解:∵将△ABC绕点A逆时针旋转得到△ADE,
点C和点E是对应点,
∴AB=AD=1,∠BAD=∠CAE=90°,
