24.1.4 图案设计 课件(共17张PPT)
文档属性
| 名称 | 24.1.4 图案设计 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 327.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 11:41:58 | ||
图片预览




文档简介
(共17张PPT)
第24章 圆
24.1 旋转
课时4 图案设计
1.设计图案.(重点)
2.如何利用平移、对称、旋转等图形变换中的一种
学习目标
或它们的组合得出图案. (难点)
新课导入
情境导入
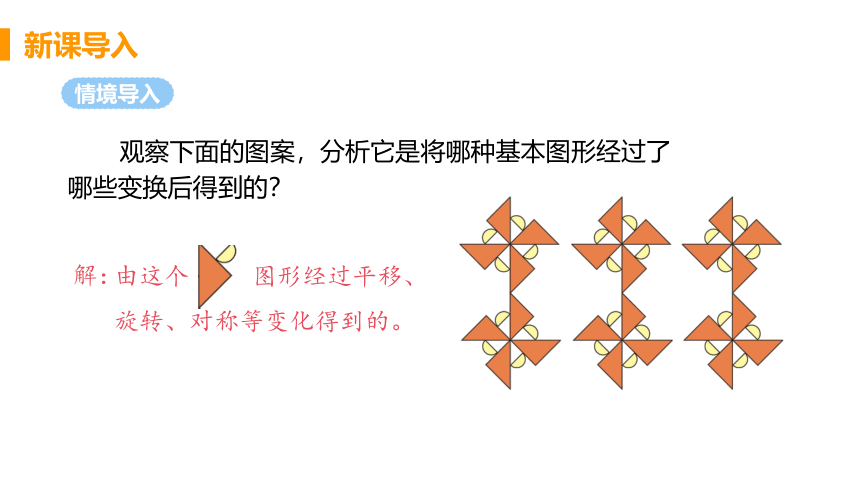
观察下面的图案,分析它是将哪种基本图形经过了哪些变换后得到的?
由这个 图形经过平移、
旋转、对称等变化得到的。
解:
新课讲解
知识点1 分析图案形成的过程
问题一:1.如图,已知线段CD是线段AB平移后的图形,D是B点的对称点,作出线段AB,并回答,AB与CD有什么位置关系.
2.如图,已知线段CD,作出线段CD关于对称轴L的对称线段C′D′,
并说明CD与对称线段C′D′之间有什么关系?
3.如图,已知线段CD,作出线段CD关于D点旋转90°的旋转后的
图形,并说明这两条线段之间有什么关系?
合作探究
新课讲解
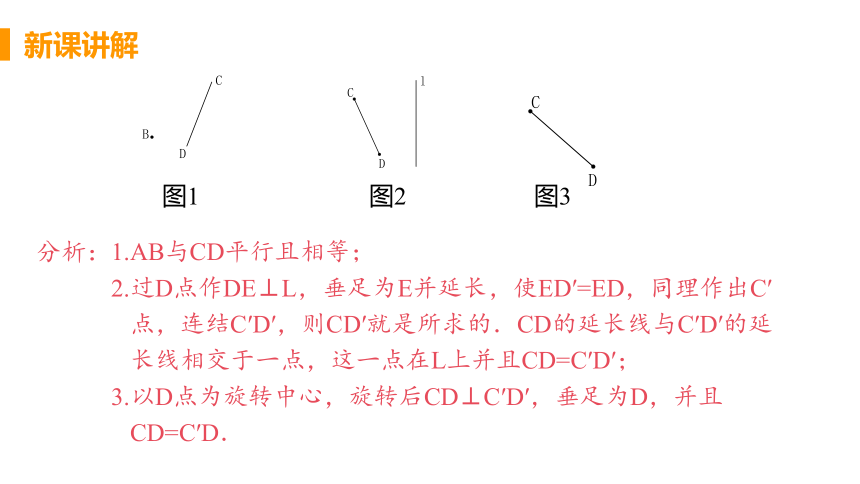
1.AB与CD平行且相等;
2.过D点作DE⊥L,垂足为E并延长,使ED′=ED,同理作出C′
点,连结C′D′,则CD′就是所求的.CD的延长线与C′D′的延
长线相交于一点,这一点在L上并且CD=C′D′;
3.以D点为旋转中心,旋转后CD⊥C′D′,垂足为D,并且
CD=C′D.
分析:
图1
图2
图3
分析图案的形成过程应按如下步骤进行:
1.划分出组成原图案的最基本的图形;
2.说明将该基本图形运用平移、旋转、轴对称中的哪
些图形变换,通过怎样的变换方式得到原图案.
结论
新课讲解
新课讲解
例
典例分析
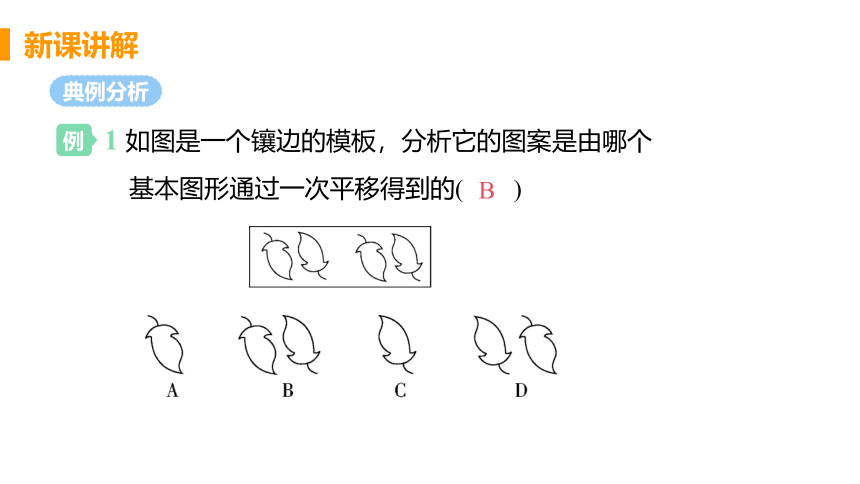
1 如图是一个镶边的模板,分析它的图案是由哪个
基本图形通过一次平移得到的( )
B
新课讲解
练一练
1
如图,若要使这个图案与自身重合,则它至少绕它的中心
旋转( )
A.45° B.90° C.135° D.180°
A
新课讲解
知识点2 图案设计
合作探究
问题二:教师提出问题:学校在艺术周上,要求学生制作一个精美的轴对称图形,请你用所给出的几何图形:○○△△--(两个圆,两个等边三角形,两条线段)为构件,构思一个独特、有意义的轴对称图形,并写上一句简要的解说词。
新课讲解
所设计图形如图所示(答案不唯一,可供参考):
新课讲解
例
2 以给出的图形“○、○、△、△、===”(两个相同的圆、两个相同
的三角形、两条线段)为构件,各设计一个构思独特且有意义
的轴对称图形和中心对称图形.举例:如图,左框中是符合
要求的一个图形.你还能构思出其他的图形吗?请在右框中
画出与之不同的图形.
典例分析
新课讲解
课堂小结
图案设计
步骤
1.划分出组成原图案的最基本的图形;
2.说明将该基本图形运用平移、旋转、
轴对称中的哪些图形变换,通过怎样的
变换方式得到原图案.
设计
当堂小练
1.根据如图所示的排列规律,“?”处应填的运算符号
是( )
A.+
B.-
C.×
D.÷
B
当堂小练
2.一个由小平行四边形组成的装饰链,断去了一部分,剩下部分如图,则断去部分的小平行四边形的个数可能是( )
A.3
B.4
C.5
D.6
C
D
拓展与延伸
1.如图所示的图案是由7个正六边形组成的,下面是三名同学对
该图案的形成过程的不同见解.
甲:该图案可看成是由其中一个正六边形经过6次平移而形成的.
乙:该图案可看成是由其图案的一半经过轴对称变换而形成的.
丙:该图案可看成是由图案的一半经过中心对称变换而形成的.
你认为上述观点都正确吗?
拓展与延伸
思路导引:解决有关分析图案的形成过程的问题时,首先应选准
基本图案,其次可以从平移、轴对称、中心对称、旋
转等角度进行分析.
解:甲从平移的角度,以一个正六边形为基本图案进行分析;乙
从轴对称的角度,以图案的一半为基本图案进行分析;丙从
中心对称的角度,以图案的一半为基本图案进行分析.虽然
各自分析的角度不同,但是他们的观点都是正确的.
第24章 圆
24.1 旋转
课时4 图案设计
1.设计图案.(重点)
2.如何利用平移、对称、旋转等图形变换中的一种
学习目标
或它们的组合得出图案. (难点)
新课导入
情境导入
观察下面的图案,分析它是将哪种基本图形经过了哪些变换后得到的?
由这个 图形经过平移、
旋转、对称等变化得到的。
解:
新课讲解
知识点1 分析图案形成的过程
问题一:1.如图,已知线段CD是线段AB平移后的图形,D是B点的对称点,作出线段AB,并回答,AB与CD有什么位置关系.
2.如图,已知线段CD,作出线段CD关于对称轴L的对称线段C′D′,
并说明CD与对称线段C′D′之间有什么关系?
3.如图,已知线段CD,作出线段CD关于D点旋转90°的旋转后的
图形,并说明这两条线段之间有什么关系?
合作探究
新课讲解
1.AB与CD平行且相等;
2.过D点作DE⊥L,垂足为E并延长,使ED′=ED,同理作出C′
点,连结C′D′,则CD′就是所求的.CD的延长线与C′D′的延
长线相交于一点,这一点在L上并且CD=C′D′;
3.以D点为旋转中心,旋转后CD⊥C′D′,垂足为D,并且
CD=C′D.
分析:
图1
图2
图3
分析图案的形成过程应按如下步骤进行:
1.划分出组成原图案的最基本的图形;
2.说明将该基本图形运用平移、旋转、轴对称中的哪
些图形变换,通过怎样的变换方式得到原图案.
结论
新课讲解
新课讲解
例
典例分析
1 如图是一个镶边的模板,分析它的图案是由哪个
基本图形通过一次平移得到的( )
B
新课讲解
练一练
1
如图,若要使这个图案与自身重合,则它至少绕它的中心
旋转( )
A.45° B.90° C.135° D.180°
A
新课讲解
知识点2 图案设计
合作探究
问题二:教师提出问题:学校在艺术周上,要求学生制作一个精美的轴对称图形,请你用所给出的几何图形:○○△△--(两个圆,两个等边三角形,两条线段)为构件,构思一个独特、有意义的轴对称图形,并写上一句简要的解说词。
新课讲解
所设计图形如图所示(答案不唯一,可供参考):
新课讲解
例
2 以给出的图形“○、○、△、△、===”(两个相同的圆、两个相同
的三角形、两条线段)为构件,各设计一个构思独特且有意义
的轴对称图形和中心对称图形.举例:如图,左框中是符合
要求的一个图形.你还能构思出其他的图形吗?请在右框中
画出与之不同的图形.
典例分析
新课讲解
课堂小结
图案设计
步骤
1.划分出组成原图案的最基本的图形;
2.说明将该基本图形运用平移、旋转、
轴对称中的哪些图形变换,通过怎样的
变换方式得到原图案.
设计
当堂小练
1.根据如图所示的排列规律,“?”处应填的运算符号
是( )
A.+
B.-
C.×
D.÷
B
当堂小练
2.一个由小平行四边形组成的装饰链,断去了一部分,剩下部分如图,则断去部分的小平行四边形的个数可能是( )
A.3
B.4
C.5
D.6
C
D
拓展与延伸
1.如图所示的图案是由7个正六边形组成的,下面是三名同学对
该图案的形成过程的不同见解.
甲:该图案可看成是由其中一个正六边形经过6次平移而形成的.
乙:该图案可看成是由其图案的一半经过轴对称变换而形成的.
丙:该图案可看成是由图案的一半经过中心对称变换而形成的.
你认为上述观点都正确吗?
拓展与延伸
思路导引:解决有关分析图案的形成过程的问题时,首先应选准
基本图案,其次可以从平移、轴对称、中心对称、旋
转等角度进行分析.
解:甲从平移的角度,以一个正六边形为基本图案进行分析;乙
从轴对称的角度,以图案的一半为基本图案进行分析;丙从
中心对称的角度,以图案的一半为基本图案进行分析.虽然
各自分析的角度不同,但是他们的观点都是正确的.
