2021-2022学年人教版数学九年级上册23.2.1中心对称课堂练习(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册23.2.1中心对称课堂练习(word版、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 432.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 21:16:51 | ||
图片预览

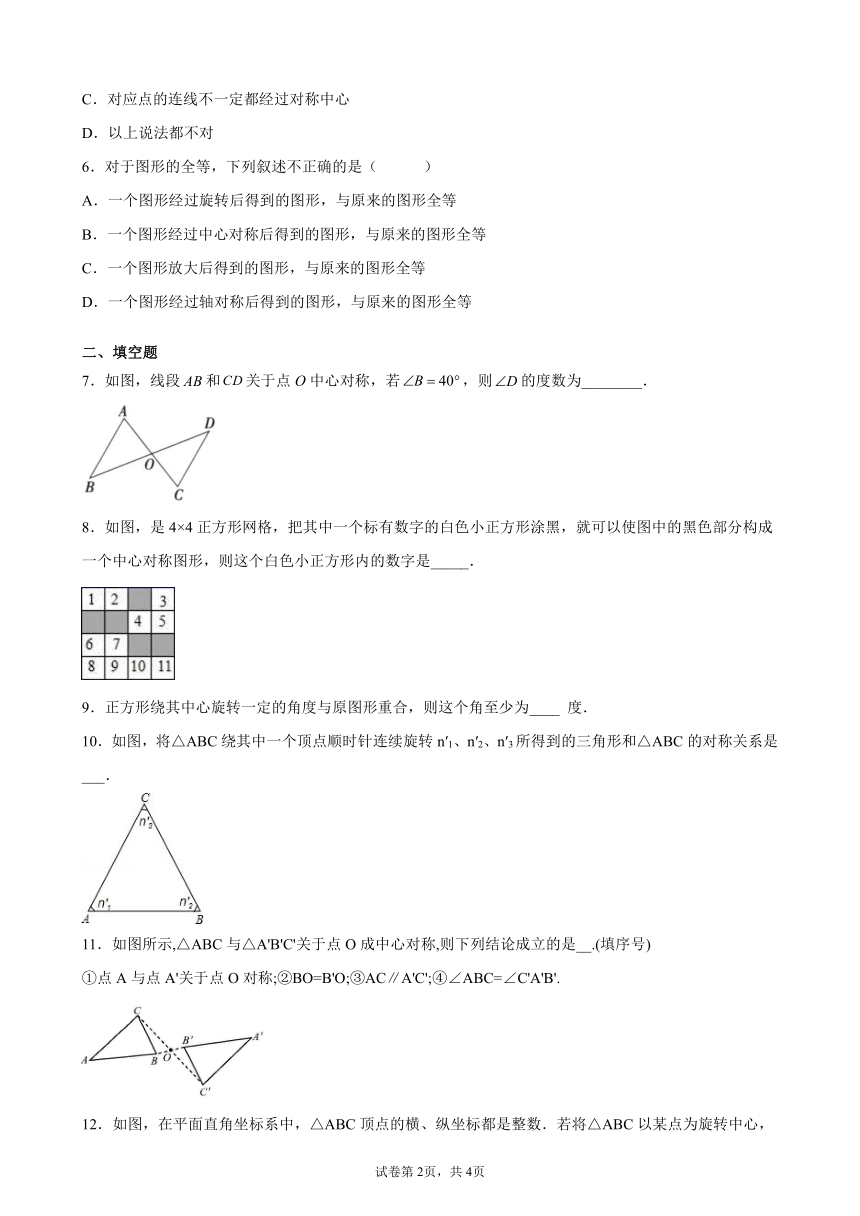

文档简介
2021-2022学年初中(人教版)数学九年级上册
23.2.1中心对称-课堂练习
时间:40分钟
一、单选题
1.如图,与关于成中心对称,不一定成立的结论是( )
A. B.
C. D.
2.如图,四边形与四边形FGHE关于点O成中心对称,下列说法中错误的是( )
A. B.
C. D.
3.关于中心对称的两个图形,对应线段的关系是 ( )
A.平行 B.相等
C.平行且相等 D.相等且平行或在同一直线上
4.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
5.关于成中心对称的两个图形的性质,下列说法正确的是( )
A.连接对应点的线段都经过对称中心,并且被对称中心平分
B.成中心对称的两个图形的对应线段不一定相等
C.对应点的连线不一定都经过对称中心
D.以上说法都不对
6.对于图形的全等,下列叙述不正确的是( )
A.一个图形经过旋转后得到的图形,与原来的图形全等
B.一个图形经过中心对称后得到的图形,与原来的图形全等
C.一个图形放大后得到的图形,与原来的图形全等
D.一个图形经过轴对称后得到的图形,与原来的图形全等
二、填空题
7.如图,线段和关于点O中心对称,若,则的度数为________.
8.如图,是4×4正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是_____.
9.正方形绕其中心旋转一定的角度与原图形重合,则这个角至少为____ 度.
10.如图,将△ABC绕其中一个顶点顺时针连续旋转n′1、n′2、n′3所得到的三角形和△ABC的对称关系是___.
11.如图所示,△ABC与△A'B'C'关于点O成中心对称,则下列结论成立的是__.(填序号)
①点A与点A'关于点O对称;②BO=B'O;③AC∥A'C';④∠ABC=∠C'A'B'.
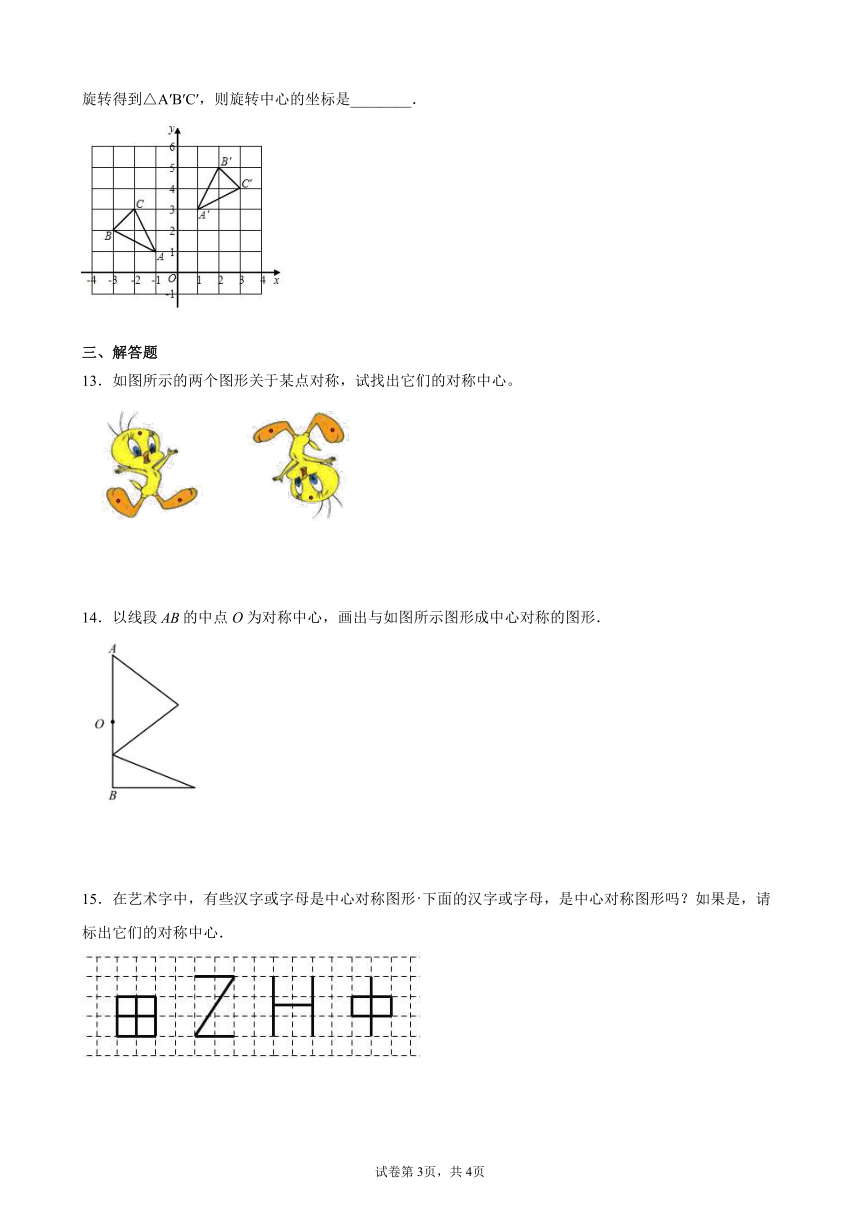
12.如图,在平面直角坐标系中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,旋转得到△A′B′C′,则旋转中心的坐标是________.
三、解答题
13.如图所示的两个图形关于某点对称,试找出它们的对称中心。
14.以线段的中点O为对称中心,画出与如图所示图形成中心对称的图形.
15.在艺术字中,有些汉字或字母是中心对称图形下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
16.如图,,交点为,点、是以为对称轴的对称点,点、是以为对称轴的对称点,试说明点、是以点为对称中心的对称点.
17.已知MN⊥PQ于点O,点A1和点A关于MN对称,点A2和点A关于PQ对称,试证明:点A1和点A2关于点O成中心对称.
18.如图,已知△ABC及点O,请用圆规和没有刻度的直尺完成下列作图:
(1)作平行四边形ABCD ;
(2)作出△ABC关于点O对称的△A'B'C'.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:对应点的连线被对称中心平分,A,B正确;
成中心对称图形的两个图形是全等形,那么对应线段相等,C正确;
和不是对应角,D错误.
故选:D.
2.D
【解析】A.∵与关于点O成中心对称,
∴,同理可得,正确;
B.∵点B与点G关于点O成中心对称,
∴,正确;
C.∵与关于点O成中心对称,
∴,同理可得,正确;
D.∵点D与点E关于点O成中心对称,
∴,
∴错误,
故选:D.
3.D
【解析】关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等,
故选D.
4.A
【解析】如图,连接HC和DE交于O1,
故选A.
5.A
【解析】根据中心对称的性质:
A. 连接对应点的线段都经过对称中心,并且被对称中心平分,此选项正确;
B. 根据成中心对称的两个图形的对应线段一定相等,故此选项错误;
C. 根据对应点的连线一定都经过对称中心,故此选项错误;
D. 以上说法都不对,此选项错误.
故答案选:A.
6.C
【解析】A. 一个图形经过旋转后得到的图形,与原来的图形全等,正确,不符合题意;
B. 一个图形经过中心对称后得到的图形,与原来的图形全等,正确,不符合题意;
C. 一个图形放大后得到的图形,与原来的图形不全等,故错误,符合题意;
D. 一个图形经过轴对称后得到的图形,与原来的图形全等,正确,不符合题意,
故选C.
7.40°
【解析】解:∵线段和关于点O成中心对称,,
∵AO=CO,BO=DO,
又∵∠AOB=∠COD,
∴(SAS),
∴,
∴的度数为.
故答案为:40°.
8.9
【解析】如图,把标有数字9的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形.
故答案为9.
9.90
【解析】∵正方形的对角线把正方形分成四个全等的直角三角形,
∴顶点处的周角被分成四个相等的角,360°÷4=90°.
∴这个正方形绕着它的中心旋转90°的整数倍后,就能与它自身重合.
∴这个角度至少是90°.
10.关于旋转点成中心对称
【解析】∵n′1+n′2+n′3=180°,
∴将△ABC绕其中一个顶点顺时针连续旋转n′1、n′2、n′3,就是将△ABC绕其中一个顶点顺时针旋转180°.
∴所得到的三角形和△ABC关于这个点成中心对称.
11.①②③
【解析】∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对称点,BO=B′O′,∠ABC=∠A′B′C′,△ABC≌△A′B′C′,△BOC≌△B′OC′,
∴∠ACB=∠A′C′B′,∠OCB=∠O′C′B′,
∴∠ACO=∠A′C′O,
∴AC∥A'C'
∴结论∠ACB=∠C′A′B′错误.
故答案为①②③
12.(1,1)
【解析】解:如图点O′即为所求.旋转中心的坐标是(1,1).
故答案为(1,1).
13.图形见解析
【解析】图形如下
14.见解析
【解析】解:如图所示:
15.是
【解析】这些艺术字均为中心对称图形,其对称中心为图形中的点O.
16.见解析.
【解析】如图,连结、、、、.
、是以为对称轴的对称点,
是的垂直平分线.
,.
同理,,.
.
.
.
、、在同一直线上,且.
点、是以点为对称中心的对称点.
17.详见解析.
【解析】解:如图:连接
∵点和点A关于MN对称,
∴
∵点和点A关于PQ对称,
∴
∴
∵
∴
∴三点共线,
∵
∴点和点关于点O成中心对称.
18.(1)见解析;(2)见解析.
【解析】(1)分别以A,C为圆心,BC,AB为半径画弧,两弧交于点D,连接CD,AD即可.
(2)连接CO,延长CO到C′,使得OC′=OC.同理作出点B′,A′,连接A′B′,B′C′,C′A′即可.
答案第1页,共2页
答案第1页,共2页
23.2.1中心对称-课堂练习
时间:40分钟
一、单选题
1.如图,与关于成中心对称,不一定成立的结论是( )
A. B.
C. D.
2.如图,四边形与四边形FGHE关于点O成中心对称,下列说法中错误的是( )
A. B.
C. D.
3.关于中心对称的两个图形,对应线段的关系是 ( )
A.平行 B.相等
C.平行且相等 D.相等且平行或在同一直线上
4.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
5.关于成中心对称的两个图形的性质,下列说法正确的是( )
A.连接对应点的线段都经过对称中心,并且被对称中心平分
B.成中心对称的两个图形的对应线段不一定相等
C.对应点的连线不一定都经过对称中心
D.以上说法都不对
6.对于图形的全等,下列叙述不正确的是( )
A.一个图形经过旋转后得到的图形,与原来的图形全等
B.一个图形经过中心对称后得到的图形,与原来的图形全等
C.一个图形放大后得到的图形,与原来的图形全等
D.一个图形经过轴对称后得到的图形,与原来的图形全等
二、填空题
7.如图,线段和关于点O中心对称,若,则的度数为________.
8.如图,是4×4正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是_____.
9.正方形绕其中心旋转一定的角度与原图形重合,则这个角至少为____ 度.
10.如图,将△ABC绕其中一个顶点顺时针连续旋转n′1、n′2、n′3所得到的三角形和△ABC的对称关系是___.
11.如图所示,△ABC与△A'B'C'关于点O成中心对称,则下列结论成立的是__.(填序号)
①点A与点A'关于点O对称;②BO=B'O;③AC∥A'C';④∠ABC=∠C'A'B'.
12.如图,在平面直角坐标系中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,旋转得到△A′B′C′,则旋转中心的坐标是________.
三、解答题
13.如图所示的两个图形关于某点对称,试找出它们的对称中心。
14.以线段的中点O为对称中心,画出与如图所示图形成中心对称的图形.
15.在艺术字中,有些汉字或字母是中心对称图形下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
16.如图,,交点为,点、是以为对称轴的对称点,点、是以为对称轴的对称点,试说明点、是以点为对称中心的对称点.
17.已知MN⊥PQ于点O,点A1和点A关于MN对称,点A2和点A关于PQ对称,试证明:点A1和点A2关于点O成中心对称.
18.如图,已知△ABC及点O,请用圆规和没有刻度的直尺完成下列作图:
(1)作平行四边形ABCD ;
(2)作出△ABC关于点O对称的△A'B'C'.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:对应点的连线被对称中心平分,A,B正确;
成中心对称图形的两个图形是全等形,那么对应线段相等,C正确;
和不是对应角,D错误.
故选:D.
2.D
【解析】A.∵与关于点O成中心对称,
∴,同理可得,正确;
B.∵点B与点G关于点O成中心对称,
∴,正确;
C.∵与关于点O成中心对称,
∴,同理可得,正确;
D.∵点D与点E关于点O成中心对称,
∴,
∴错误,
故选:D.
3.D
【解析】关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等,
故选D.
4.A
【解析】如图,连接HC和DE交于O1,
故选A.
5.A
【解析】根据中心对称的性质:
A. 连接对应点的线段都经过对称中心,并且被对称中心平分,此选项正确;
B. 根据成中心对称的两个图形的对应线段一定相等,故此选项错误;
C. 根据对应点的连线一定都经过对称中心,故此选项错误;
D. 以上说法都不对,此选项错误.
故答案选:A.
6.C
【解析】A. 一个图形经过旋转后得到的图形,与原来的图形全等,正确,不符合题意;
B. 一个图形经过中心对称后得到的图形,与原来的图形全等,正确,不符合题意;
C. 一个图形放大后得到的图形,与原来的图形不全等,故错误,符合题意;
D. 一个图形经过轴对称后得到的图形,与原来的图形全等,正确,不符合题意,
故选C.
7.40°
【解析】解:∵线段和关于点O成中心对称,,
∵AO=CO,BO=DO,
又∵∠AOB=∠COD,
∴(SAS),
∴,
∴的度数为.
故答案为:40°.
8.9
【解析】如图,把标有数字9的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形.
故答案为9.
9.90
【解析】∵正方形的对角线把正方形分成四个全等的直角三角形,
∴顶点处的周角被分成四个相等的角,360°÷4=90°.
∴这个正方形绕着它的中心旋转90°的整数倍后,就能与它自身重合.
∴这个角度至少是90°.
10.关于旋转点成中心对称
【解析】∵n′1+n′2+n′3=180°,
∴将△ABC绕其中一个顶点顺时针连续旋转n′1、n′2、n′3,就是将△ABC绕其中一个顶点顺时针旋转180°.
∴所得到的三角形和△ABC关于这个点成中心对称.
11.①②③
【解析】∵△ABC与△A′B′C′关于点O成中心对称,
∴点A与点A′是对称点,BO=B′O′,∠ABC=∠A′B′C′,△ABC≌△A′B′C′,△BOC≌△B′OC′,
∴∠ACB=∠A′C′B′,∠OCB=∠O′C′B′,
∴∠ACO=∠A′C′O,
∴AC∥A'C'
∴结论∠ACB=∠C′A′B′错误.
故答案为①②③
12.(1,1)
【解析】解:如图点O′即为所求.旋转中心的坐标是(1,1).
故答案为(1,1).
13.图形见解析
【解析】图形如下
14.见解析
【解析】解:如图所示:
15.是
【解析】这些艺术字均为中心对称图形,其对称中心为图形中的点O.
16.见解析.
【解析】如图,连结、、、、.
、是以为对称轴的对称点,
是的垂直平分线.
,.
同理,,.
.
.
.
、、在同一直线上,且.
点、是以点为对称中心的对称点.
17.详见解析.
【解析】解:如图:连接
∵点和点A关于MN对称,
∴
∵点和点A关于PQ对称,
∴
∴
∵
∴
∴三点共线,
∵
∴点和点关于点O成中心对称.
18.(1)见解析;(2)见解析.
【解析】(1)分别以A,C为圆心,BC,AB为半径画弧,两弧交于点D,连接CD,AD即可.
(2)连接CO,延长CO到C′,使得OC′=OC.同理作出点B′,A′,连接A′B′,B′C′,C′A′即可.
答案第1页,共2页
答案第1页,共2页
同课章节目录
