24.2.4 圆的确定 课件(共24张PPT)
文档属性
| 名称 | 24.2.4 圆的确定 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 263.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 17:42:42 | ||
图片预览



文档简介
(共24张PPT)
第24章 圆
24.2 圆的基本性质
课时4 圆的确定
1.理解并掌握确定圆的条件.
2.理解三角形的外接圆,三角形外心的概念,能够运用其性质进行计算. (重点)
3.理解反证法的思想,能够运用反证法证明命题.(难点)
学习目标
新课导入
情境导入
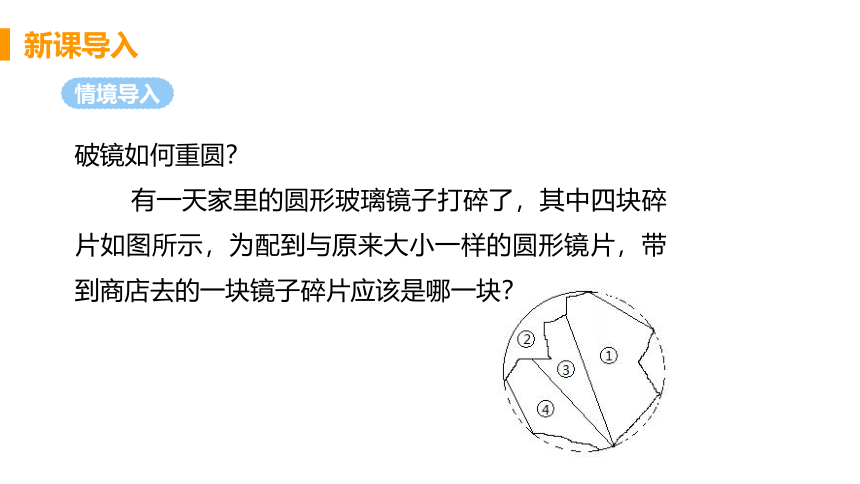
破镜如何重圆?
有一天家里的圆形玻璃镜子打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形镜片,带到商店去的一块镜子碎片应该是哪一块?
新课讲解
知识点1 圆的确定
合作探究
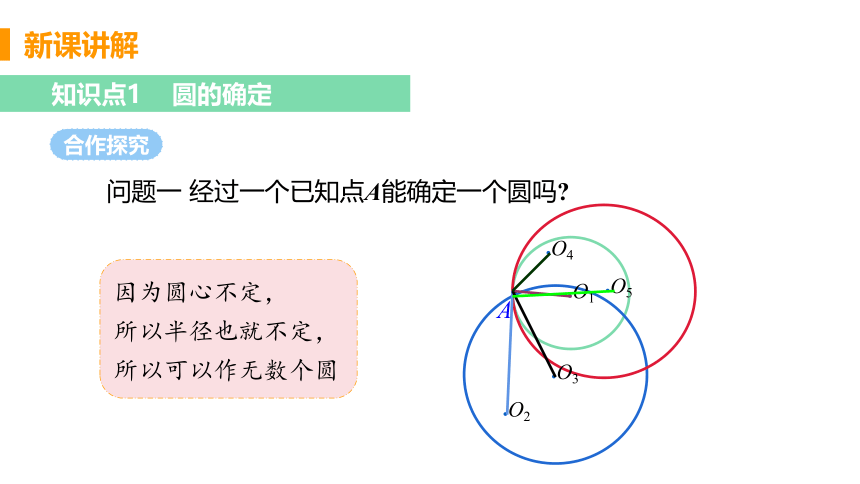
问题一 经过一个已知点A能确定一个圆吗
A
●O1
●O2
●O3
●O5
●O4
因为圆心不定,
所以半径也就不定,
所以可以作无数个圆
新课讲解
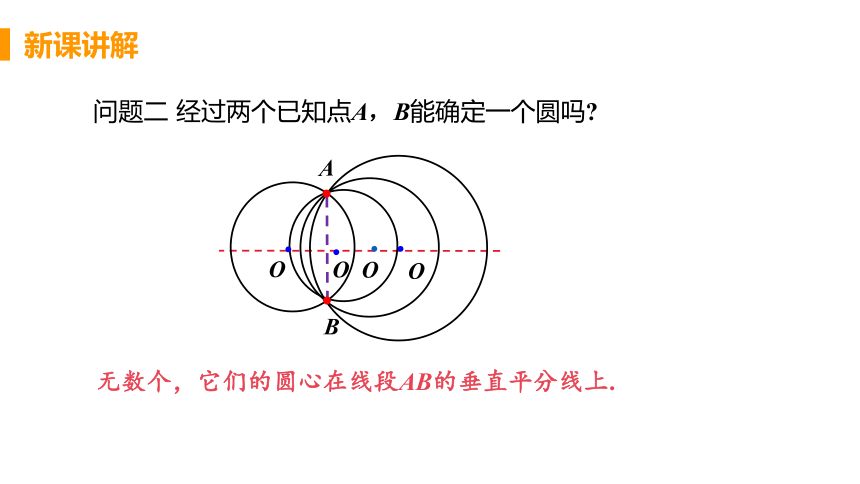
问题二 经过两个已知点A,B能确定一个圆吗
●
O
O
●
●
O
●
O
A
B
无数个,它们的圆心在线段AB的垂直平分线上.
新课讲解
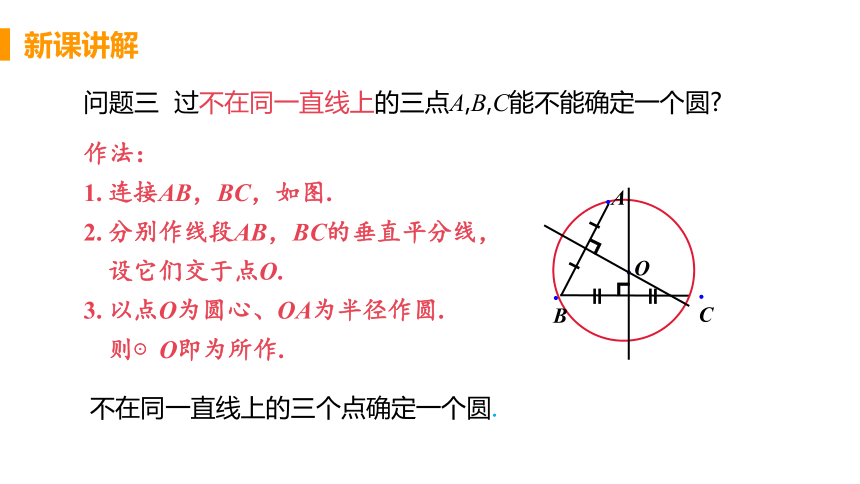
问题三 过不在同一直线上的三点A,B,C能不能确定一个圆
作法:
连接AB,BC,如图.
分别作线段AB,BC的垂直平分线,设它们交于点O.
以点O为圆心、OA为半径作圆.
则⊙O即为所作.
●
B
●A
● O
┓
┏
不在同一直线上的三个点确定一个圆.
●
C
新课讲解
例
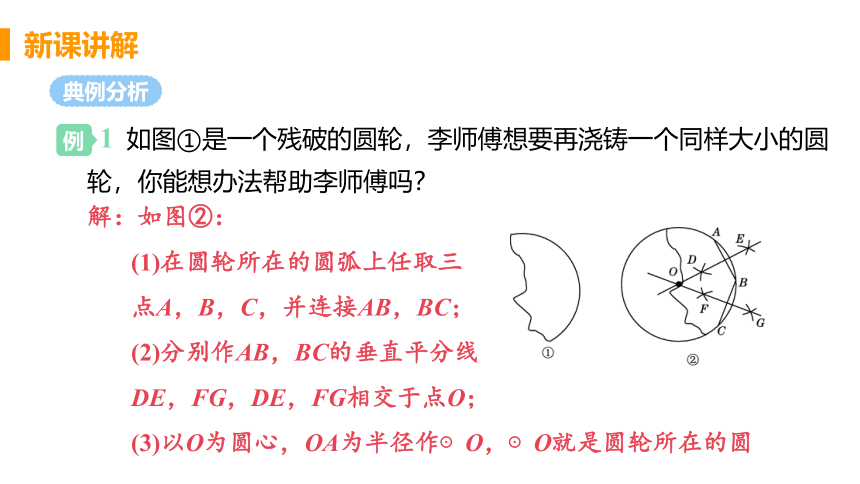
1 如图①是一个残破的圆轮,李师傅想要再浇铸一个同样大小的圆轮,你能想办法帮助李师傅吗?
典例分析
解:如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所在的圆
新课讲解
练一练
1
2
如图,点A,B,C 在同一条直线上,点D 在直线AB 外,
过这四个点中的任意三个点,能画圆的个数是( )
A.1 B.2 C.3 D.4
已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个
C
B
新课讲解
知识点2 三角形的外接圆
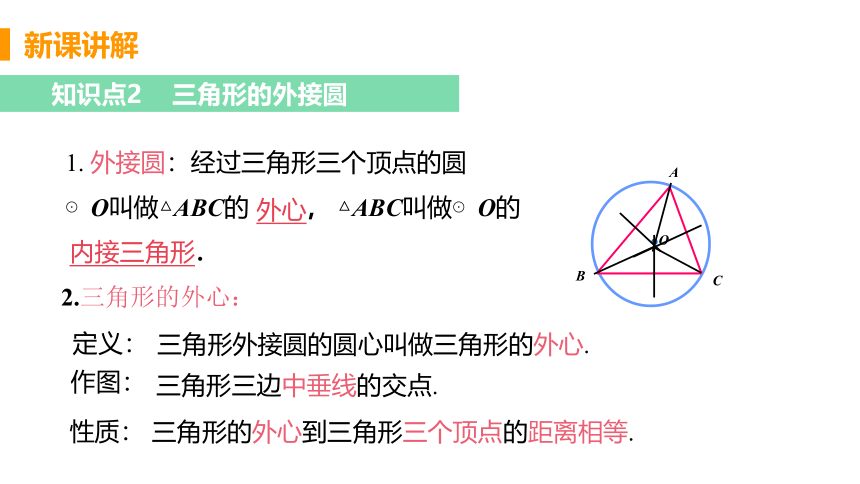
1. 外接圆:经过三角形三个顶点的圆
⊙O叫做△ABC的 , △ABC叫做⊙O的
.
三角形的外心到三角形三个顶点的距离相等.
2.三角形的外心:
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边中垂线的交点.
性质:
定义:
●O
A
B
C
外心
内接三角形
新课讲解
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
锐角三角形:内部
直角三角形:
斜边中点
钝角三角形:外部
新课讲解
例
2
典例分析
如图,在△ABC中,BC= cm,AB=AC,∠BAC=120°.
(1)尺规作图:作△ABC的外接圆(只需作出图形,并
保留作图痕迹);
(2)求它的外接圆半径.
解:(1)如图,⊙P即
为所求作的圆.
解:
(2)如上图,连接PC.设AP与BC交于点M,
∵BC=6 cm,
AB=AC,∠BAC=120°,BC⊥AP,
∴∠CAP=60°,BM=MC=3 cm,
又∵PA=PC,
∴△APC是等边三角形,∠MPC=60°.
∵在Rt△MPC中,
sin ∠MPC=sin 60°=
∴PC= =6(cm).
∴它的外接圆半径为6 cm.
新课讲解
新课讲解
练一练
1
如图,AC,BE是⊙O的直径,弦AD与BE 交于点F,下列三角形中,外心不是点O的是( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE
B
新课讲解
2
如图,在平面直角坐标系xOy中,点A的坐标为(0,3),
点B的坐标为(2,1),点C的坐标为(2,-3),则△ABC
的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(-2,-1)
D.(2,0)
C
新课讲解
知识点03 反证法
问题一 经过同一条直线上的三个点能作出一个圆吗?
A
B
C
如图,假设经过直线l上的三点A、B、C可以作圆,设这个圆的圆心为O,
由OA=OB,点O在AB的垂直平分线l1上;
由OB=OC,点O在BC的垂直平分线l2上;
因为,AB和BC都在直线l上
这样,经过点O便有两条直线l1,l2都垂直于直线l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,
所以,假设错误,过同一条直线上的三点不能作圆.
新课讲解
l1
l2
A
B
C
O
新课讲解
上面的证明不是直接从题设推出结论,而是先假设命题结论不成立,然后经过推理,得出矛盾的结果,最后断言结论一定成立,这样的证明方法叫做反证法.
①反设:假设命题的结论不成立;
②推理:从①中的“反设”出发,逐步推理直至出现与已知条件、
定义、基本事实、定理等中任一相矛盾的结果;
③结论:由矛盾的结果判定①中的“反设”不成立,从而肯定命
题的结论成立.
反证法的一般步骤:
新课讲解
例
典例分析
3 已知:如图,直线AB//直线CD,直线EF分别交 AB, CD 于
点O1,O2. 求证: ∠EO1B=∠EO2D
A
B
C
D
E
F
O1
O2
A'
B'
新课讲解
证明:假设∠EO1B≠∠EO2D ,
过点O1作直线A ' B ' ,使 ∠EO1B ' =∠EO2D.
根据“同位角相等,两直线平行”,得A' B ' //CD.
这样,过点O1就有两条直线AB , A ' B '平行于直线
CD,这与“过直线外一点有且只有一条直线与这条
直线平行”相矛盾,
即∠EO1B≠∠EO2D的假设不成立,
所以∠EO1B=∠EO2D.
课堂小结
圆的确定
圆的确定
三角形的外接圆
反证法
不在同一直线上的三个点确定一个圆
外接圆
外心
内接三角形
三角形外心的到三角形的三个顶点距离相等
反设
推理
正轮
当堂小练
1.下列关于确定一个圆的说法中,正确的是( )
A.三个点一定能确定一个圆
B.以已知线段为半径能确定一个圆
C.以已知线段为直径能确定一个圆
D.菱形的四个顶点能确定一个圆
2.等腰三角形底边上的高与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定.
D
C
当堂小练
3. 用反证法证明:一个圆只有一个圆心.
证明:假设⊙O有两个圆心O及O′,
在圆内任作一弦AB,设弦AB的中点为P,
连结OP,O′P,则OP⊥AB,O′P⊥AB,
过直线AB上一点P,同时有两条直线OP,
O′P都垂直于AB,与垂线的性质矛盾,
故一个圆只有一个圆心.
D
拓展与延伸
1. 小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,
如图,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,
保留作图痕迹);
(2)若在△ABC中,AB=8米,AC=6米,∠BAC=90°,
试求小明家圆形花坛的面积.
解:(1)如图所示,☉O就是花坛的位置
(2)∵∠BAC=90°,
∴BC是☉O的直径.
∵AB=8米,AC=6米,
∴BC=10米,
∴△ABC外接圆的半径为5米,
∴小明家圆形花坛的面积为25π平方米.
拓展与延伸
第24章 圆
24.2 圆的基本性质
课时4 圆的确定
1.理解并掌握确定圆的条件.
2.理解三角形的外接圆,三角形外心的概念,能够运用其性质进行计算. (重点)
3.理解反证法的思想,能够运用反证法证明命题.(难点)
学习目标
新课导入
情境导入
破镜如何重圆?
有一天家里的圆形玻璃镜子打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形镜片,带到商店去的一块镜子碎片应该是哪一块?
新课讲解
知识点1 圆的确定
合作探究
问题一 经过一个已知点A能确定一个圆吗
A
●O1
●O2
●O3
●O5
●O4
因为圆心不定,
所以半径也就不定,
所以可以作无数个圆
新课讲解
问题二 经过两个已知点A,B能确定一个圆吗
●
O
O
●
●
O
●
O
A
B
无数个,它们的圆心在线段AB的垂直平分线上.
新课讲解
问题三 过不在同一直线上的三点A,B,C能不能确定一个圆
作法:
连接AB,BC,如图.
分别作线段AB,BC的垂直平分线,设它们交于点O.
以点O为圆心、OA为半径作圆.
则⊙O即为所作.
●
B
●A
● O
┓
┏
不在同一直线上的三个点确定一个圆.
●
C
新课讲解
例
1 如图①是一个残破的圆轮,李师傅想要再浇铸一个同样大小的圆轮,你能想办法帮助李师傅吗?
典例分析
解:如图②:
(1)在圆轮所在的圆弧上任取三
点A,B,C,并连接AB,BC;
(2)分别作AB,BC的垂直平分线
DE,FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,⊙O就是圆轮所在的圆
新课讲解
练一练
1
2
如图,点A,B,C 在同一条直线上,点D 在直线AB 外,
过这四个点中的任意三个点,能画圆的个数是( )
A.1 B.2 C.3 D.4
已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个
C
B
新课讲解
知识点2 三角形的外接圆
1. 外接圆:经过三角形三个顶点的圆
⊙O叫做△ABC的 , △ABC叫做⊙O的
.
三角形的外心到三角形三个顶点的距离相等.
2.三角形的外心:
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边中垂线的交点.
性质:
定义:
●O
A
B
C
外心
内接三角形
新课讲解
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
锐角三角形:内部
直角三角形:
斜边中点
钝角三角形:外部
新课讲解
例
2
典例分析
如图,在△ABC中,BC= cm,AB=AC,∠BAC=120°.
(1)尺规作图:作△ABC的外接圆(只需作出图形,并
保留作图痕迹);
(2)求它的外接圆半径.
解:(1)如图,⊙P即
为所求作的圆.
解:
(2)如上图,连接PC.设AP与BC交于点M,
∵BC=6 cm,
AB=AC,∠BAC=120°,BC⊥AP,
∴∠CAP=60°,BM=MC=3 cm,
又∵PA=PC,
∴△APC是等边三角形,∠MPC=60°.
∵在Rt△MPC中,
sin ∠MPC=sin 60°=
∴PC= =6(cm).
∴它的外接圆半径为6 cm.
新课讲解
新课讲解
练一练
1
如图,AC,BE是⊙O的直径,弦AD与BE 交于点F,下列三角形中,外心不是点O的是( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE
B
新课讲解
2
如图,在平面直角坐标系xOy中,点A的坐标为(0,3),
点B的坐标为(2,1),点C的坐标为(2,-3),则△ABC
的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(-2,-1)
D.(2,0)
C
新课讲解
知识点03 反证法
问题一 经过同一条直线上的三个点能作出一个圆吗?
A
B
C
如图,假设经过直线l上的三点A、B、C可以作圆,设这个圆的圆心为O,
由OA=OB,点O在AB的垂直平分线l1上;
由OB=OC,点O在BC的垂直平分线l2上;
因为,AB和BC都在直线l上
这样,经过点O便有两条直线l1,l2都垂直于直线l,这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,
所以,假设错误,过同一条直线上的三点不能作圆.
新课讲解
l1
l2
A
B
C
O
新课讲解
上面的证明不是直接从题设推出结论,而是先假设命题结论不成立,然后经过推理,得出矛盾的结果,最后断言结论一定成立,这样的证明方法叫做反证法.
①反设:假设命题的结论不成立;
②推理:从①中的“反设”出发,逐步推理直至出现与已知条件、
定义、基本事实、定理等中任一相矛盾的结果;
③结论:由矛盾的结果判定①中的“反设”不成立,从而肯定命
题的结论成立.
反证法的一般步骤:
新课讲解
例
典例分析
3 已知:如图,直线AB//直线CD,直线EF分别交 AB, CD 于
点O1,O2. 求证: ∠EO1B=∠EO2D
A
B
C
D
E
F
O1
O2
A'
B'
新课讲解
证明:假设∠EO1B≠∠EO2D ,
过点O1作直线A ' B ' ,使 ∠EO1B ' =∠EO2D.
根据“同位角相等,两直线平行”,得A' B ' //CD.
这样,过点O1就有两条直线AB , A ' B '平行于直线
CD,这与“过直线外一点有且只有一条直线与这条
直线平行”相矛盾,
即∠EO1B≠∠EO2D的假设不成立,
所以∠EO1B=∠EO2D.
课堂小结
圆的确定
圆的确定
三角形的外接圆
反证法
不在同一直线上的三个点确定一个圆
外接圆
外心
内接三角形
三角形外心的到三角形的三个顶点距离相等
反设
推理
正轮
当堂小练
1.下列关于确定一个圆的说法中,正确的是( )
A.三个点一定能确定一个圆
B.以已知线段为半径能确定一个圆
C.以已知线段为直径能确定一个圆
D.菱形的四个顶点能确定一个圆
2.等腰三角形底边上的高与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定.
D
C
当堂小练
3. 用反证法证明:一个圆只有一个圆心.
证明:假设⊙O有两个圆心O及O′,
在圆内任作一弦AB,设弦AB的中点为P,
连结OP,O′P,则OP⊥AB,O′P⊥AB,
过直线AB上一点P,同时有两条直线OP,
O′P都垂直于AB,与垂线的性质矛盾,
故一个圆只有一个圆心.
D
拓展与延伸
1. 小明家的房前有一块矩形的空地,空地上有三棵树A,B,C,
如图,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,
保留作图痕迹);
(2)若在△ABC中,AB=8米,AC=6米,∠BAC=90°,
试求小明家圆形花坛的面积.
解:(1)如图所示,☉O就是花坛的位置
(2)∵∠BAC=90°,
∴BC是☉O的直径.
∵AB=8米,AC=6米,
∴BC=10米,
∴△ABC外接圆的半径为5米,
∴小明家圆形花坛的面积为25π平方米.
拓展与延伸
