山西省山大附中2013届高三10月月考数学文试题
文档属性
| 名称 | 山西省山大附中2013届高三10月月考数学文试题 |  | |
| 格式 | zip | ||
| 文件大小 | 340.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-11 20:53:05 | ||
图片预览




文档简介
山西大学附中
2012~2013学年第一学期高三(10月)月考
数 学 试 题(文)
(考查时间:120分钟)
一.选择题(每小题5分,共60分)
1. 已知全集则( )
A. B. C. D.
2. 复数在复平面上对应的点的坐标是( )
A. B. C. D.
3.老师给学生出了一道题,“试写一个程序框图,计算S=1++++”.发现同学们有如下几种做法,其中有一个是错误的,这个错误的做法是 ( )
4.对任意,恒成立,则的取值范围是( )
A. B. C. D.
5.在△中,已知是边上一点,若,则=( )
A. B. C. D.
6.设0<<1,函数,则使的x的取值范围是
A. B. C. D.
7. 已知为等比数列,是它的前项和。若, 且与的等差中项为,则=( )21世纪教育网
A. B. C. D.
8.设为偶函数,对于任意的的数,都有,已知,那么等于( )
A. B. C. D.
9.设函数,其中,则导数的取值范围是( )
A. B. C. D.
10.双曲线的渐近线与抛物线相切,则该双曲线的离心率等于( )
A. B. C. D.
11.已知函数在处有极值,则等于( )
A.或 B. C. D.或http://21世纪教育网/ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
12.已知正方体的棱长为, 长为的线段的一个端点在棱 上运动, 另一端点在正方形内运动, 则的中点的轨迹的面积( )
A. B. C. D.
二、填空题:(每小题5分,共20分)
13.学校为了调查学生在课外读物方面的支出情况,
抽出了一个容量 为的样本,其频率分布直方图如图所示,
其中支出在元的同学有人,则的值为____.
14.幂函数的图像过原点,则实数的值等于 .
15.设是半径为的球面上的四个不同点,且满足,,,用分别表示△、△、△的面积,则的最大值是 .
16.给出以下四个命题:
①已知命题 ;命题则命题是真命题;
②过点且在轴和轴上的截距相等的直线方程是;
③函数在定义域内有且只有一个零点;21世纪教育网
④若直线和直线垂直,则角
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
山西大学附中10月月考数学(文科)答卷纸
一.选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二.填空题:(每小题5分,共20分)
13.________ 14._________ _
15. 16.____ _______
三、解答题:(本大题共70分)
17.(本小题10分)已知A, B,C为锐角的三个内角,向量, ,且.
(I)求的大小;
(II)求取最大值时角的大小.
18. (本小题12分)已知各项都不相等的等差数列的前项和为,且为和的等比中项.
(I)求数列的通项公式;
(II)若数列满足,且,求数列的前项和。
21世纪教育网
19.(本小题12分)有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有道题的问卷到各学校做问卷调查.某中学两个班各被随机抽取名学生接受问卷调查,班名学生得分为:,,,,;班5名学生得分为:,,,,.
(Ⅰ)请你估计两个班中哪个班的问卷得分要稳定一些;
(Ⅱ)如果把班名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为的样本,求样本平均数与总体平均数之差的绝对值不小于的概率.
21世纪教育网
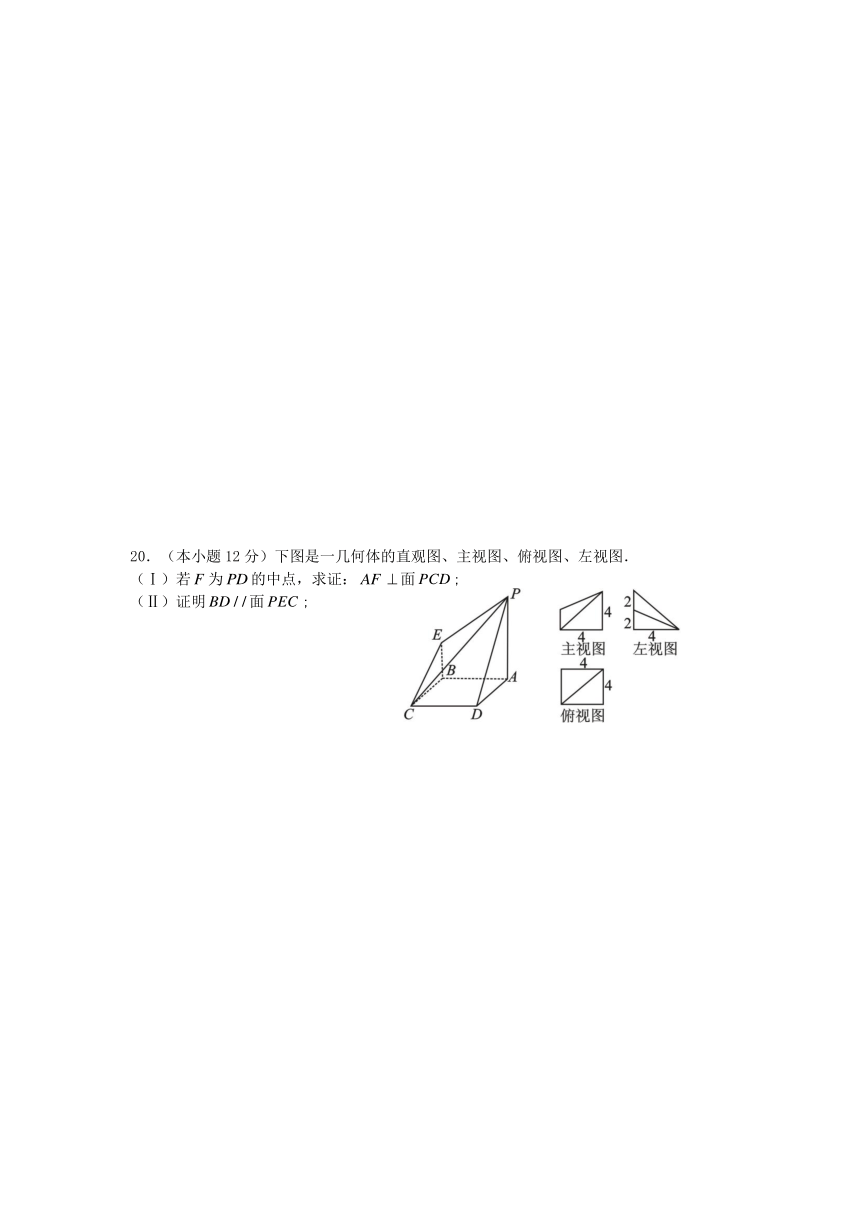
20.(本小题12分)下图是一几何体的直观图、主视图、俯视图、左视图.
(Ⅰ)若为的中点,求证:面;
(Ⅱ)证明面;
21.(本小题12分)设椭圆的离心率,右焦点到直线的距离O为坐标原点。
(I)求椭圆C的方程;
(II)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值。
22. (本小题12分)已知函数,是的一个零点,又在处有极值,在区间和上是单调的,且在这两个区间上的单调性相反.
(I)求的取值范围;
(II)当时,求使成立的实数的取值范围.
山西大学附中10月月考数学(文理)参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D C A A C C D A A C D
二.填空题: 13. 100 14.(文)4, 理 -192
15. 8 16. ①③
三、解答题:
17.解:(Ⅰ),
. ……………3分
是锐角三角形,. ………5分
(Ⅱ)是锐角三角形,且,
………7分
………9分
当取最大值时,即. ……………10分
18.解:(Ⅰ)设等差数列的公差为(),
则 解得 ∴.
(Ⅱ)由, ∴,
.
∴.
∴
.
19.(文科做)解:(Ⅰ)∵班的名学生的平均得分为÷,
方差;……3分
班的名学生的平均得分为÷, ……………………4分
方差. ……6分
∴ ,
∴ 班的预防知识的问卷得分要稳定一些. ………………………………8分
(Ⅱ)从班名同学中任选名同学的方法共有种, …………………10分
其中样本和,和,和,和的平均数满足条件,故所求概率为. ……………………12分
19.(理科做)解:(1)设A通过体能、射击、反应分别记为事件M、N、P则http://21世纪教育网/ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )A能够入选包含以下几个互斥事件:
http://21世纪教育网/ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
(6分)http://21世纪教育网/ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
(2)记表示该训练基地得到的训练经费
0 3000 6000 9000 12000
P
(元) (12分)
20.解: (Ⅰ)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥面ABCD,
PA∥EB,PA=2EB=4.∵PA=AD,F为PD的中点,
∴PD⊥AF,又∵CD⊥DA,CD⊥PA,PA∩DA=A,
∴CD⊥面ADP,∴CD⊥AF.又CD∩DP=D, ∴AF⊥面PCD. ---------- 4分
(Ⅱ)取PC的中点M,AC与BD的交点为N,连结MN,
∴MN=PA,MN∥PA,
∴MN=EB,MN∥EB,故四边形BEMN为平行四边形,
∴EM∥BN,又EM面PEC,∴BD∥面PEC. -------------7分
(理科)(Ⅲ)分别以BC,BA,BE为x,y,z轴建立空间直角坐标系,
则C( 4,0,0),D(4 ,4 , 0),E(0,0,2),A(0,4 ,0),P(0,4,4),
∵F为PD的中点,∴F(2,4,2). ∵AF⊥面PCD,∴为面PCD的一个法向量,
=(-2,0,-2),设平面PEC的法向量为=(x,y ,z),
则, ∴,令x=1,∴, ---10分
∴∴与的夹角为.
面PEC与面PDC所成的二面角(锐角)的余弦值为. ----12分
21.. 解:(I)由
由右焦点到直线的距离为
得:解得 所以椭圆C的方程为
(II)设,直线AB的方程为
与椭圆联立消去y得
即
整理得
所以O到直线AB的距离
……8分
,当且仅当OA=OB时取“=”号。
由
即弦AB的长度的最小值是
22.解:(Ⅰ)因为,所以
又在处有极值,所以即……………………2分
所以 令 所以或
又因为在区间上是单调且单调性相反
所以所以 …………………6分
(Ⅱ)因为,且是的一个零点,21世纪教育网
所以,所以,从而
所以,令,所以或…………8分
列表讨论如下:列表讨论如下:
0 2
+ — 0 — + 0 + —
0
所以当时,若,则
当时,若,则
从而 或即或
所以存在实数,满足题目要求。
21世纪教育网
2012~2013学年第一学期高三(10月)月考
数 学 试 题(文)
(考查时间:120分钟)
一.选择题(每小题5分,共60分)
1. 已知全集则( )
A. B. C. D.
2. 复数在复平面上对应的点的坐标是( )
A. B. C. D.
3.老师给学生出了一道题,“试写一个程序框图,计算S=1++++”.发现同学们有如下几种做法,其中有一个是错误的,这个错误的做法是 ( )
4.对任意,恒成立,则的取值范围是( )
A. B. C. D.
5.在△中,已知是边上一点,若,则=( )
A. B. C. D.
6.设0<<1,函数,则使的x的取值范围是
A. B. C. D.
7. 已知为等比数列,是它的前项和。若, 且与的等差中项为,则=( )21世纪教育网
A. B. C. D.
8.设为偶函数,对于任意的的数,都有,已知,那么等于( )
A. B. C. D.
9.设函数,其中,则导数的取值范围是( )
A. B. C. D.
10.双曲线的渐近线与抛物线相切,则该双曲线的离心率等于( )
A. B. C. D.
11.已知函数在处有极值,则等于( )
A.或 B. C. D.或http://21世纪教育网/ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
12.已知正方体的棱长为, 长为的线段的一个端点在棱 上运动, 另一端点在正方形内运动, 则的中点的轨迹的面积( )
A. B. C. D.
二、填空题:(每小题5分,共20分)
13.学校为了调查学生在课外读物方面的支出情况,
抽出了一个容量 为的样本,其频率分布直方图如图所示,
其中支出在元的同学有人,则的值为____.
14.幂函数的图像过原点,则实数的值等于 .
15.设是半径为的球面上的四个不同点,且满足,,,用分别表示△、△、△的面积,则的最大值是 .
16.给出以下四个命题:
①已知命题 ;命题则命题是真命题;
②过点且在轴和轴上的截距相等的直线方程是;
③函数在定义域内有且只有一个零点;21世纪教育网
④若直线和直线垂直,则角
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
山西大学附中10月月考数学(文科)答卷纸
一.选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二.填空题:(每小题5分,共20分)
13.________ 14._________ _
15. 16.____ _______
三、解答题:(本大题共70分)
17.(本小题10分)已知A, B,C为锐角的三个内角,向量, ,且.
(I)求的大小;
(II)求取最大值时角的大小.
18. (本小题12分)已知各项都不相等的等差数列的前项和为,且为和的等比中项.
(I)求数列的通项公式;
(II)若数列满足,且,求数列的前项和。
21世纪教育网
19.(本小题12分)有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有道题的问卷到各学校做问卷调查.某中学两个班各被随机抽取名学生接受问卷调查,班名学生得分为:,,,,;班5名学生得分为:,,,,.
(Ⅰ)请你估计两个班中哪个班的问卷得分要稳定一些;
(Ⅱ)如果把班名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为的样本,求样本平均数与总体平均数之差的绝对值不小于的概率.
21世纪教育网
20.(本小题12分)下图是一几何体的直观图、主视图、俯视图、左视图.
(Ⅰ)若为的中点,求证:面;
(Ⅱ)证明面;
21.(本小题12分)设椭圆的离心率,右焦点到直线的距离O为坐标原点。
(I)求椭圆C的方程;
(II)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值。
22. (本小题12分)已知函数,是的一个零点,又在处有极值,在区间和上是单调的,且在这两个区间上的单调性相反.
(I)求的取值范围;
(II)当时,求使成立的实数的取值范围.
山西大学附中10月月考数学(文理)参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D C A A C C D A A C D
二.填空题: 13. 100 14.(文)4, 理 -192
15. 8 16. ①③
三、解答题:
17.解:(Ⅰ),
. ……………3分
是锐角三角形,. ………5分
(Ⅱ)是锐角三角形,且,
………7分
………9分
当取最大值时,即. ……………10分
18.解:(Ⅰ)设等差数列的公差为(),
则 解得 ∴.
(Ⅱ)由, ∴,
.
∴.
∴
.
19.(文科做)解:(Ⅰ)∵班的名学生的平均得分为÷,
方差;……3分
班的名学生的平均得分为÷, ……………………4分
方差. ……6分
∴ ,
∴ 班的预防知识的问卷得分要稳定一些. ………………………………8分
(Ⅱ)从班名同学中任选名同学的方法共有种, …………………10分
其中样本和,和,和,和的平均数满足条件,故所求概率为. ……………………12分
19.(理科做)解:(1)设A通过体能、射击、反应分别记为事件M、N、P则http://21世纪教育网/ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )A能够入选包含以下几个互斥事件:
http://21世纪教育网/ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
(6分)http://21世纪教育网/ ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
(2)记表示该训练基地得到的训练经费
0 3000 6000 9000 12000
P
(元) (12分)
20.解: (Ⅰ)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥面ABCD,
PA∥EB,PA=2EB=4.∵PA=AD,F为PD的中点,
∴PD⊥AF,又∵CD⊥DA,CD⊥PA,PA∩DA=A,
∴CD⊥面ADP,∴CD⊥AF.又CD∩DP=D, ∴AF⊥面PCD. ---------- 4分
(Ⅱ)取PC的中点M,AC与BD的交点为N,连结MN,
∴MN=PA,MN∥PA,
∴MN=EB,MN∥EB,故四边形BEMN为平行四边形,
∴EM∥BN,又EM面PEC,∴BD∥面PEC. -------------7分
(理科)(Ⅲ)分别以BC,BA,BE为x,y,z轴建立空间直角坐标系,
则C( 4,0,0),D(4 ,4 , 0),E(0,0,2),A(0,4 ,0),P(0,4,4),
∵F为PD的中点,∴F(2,4,2). ∵AF⊥面PCD,∴为面PCD的一个法向量,
=(-2,0,-2),设平面PEC的法向量为=(x,y ,z),
则, ∴,令x=1,∴, ---10分
∴∴与的夹角为.
面PEC与面PDC所成的二面角(锐角)的余弦值为. ----12分
21.. 解:(I)由
由右焦点到直线的距离为
得:解得 所以椭圆C的方程为
(II)设,直线AB的方程为
与椭圆联立消去y得
即
整理得
所以O到直线AB的距离
……8分
,当且仅当OA=OB时取“=”号。
由
即弦AB的长度的最小值是
22.解:(Ⅰ)因为,所以
又在处有极值,所以即……………………2分
所以 令 所以或
又因为在区间上是单调且单调性相反
所以所以 …………………6分
(Ⅱ)因为,且是的一个零点,21世纪教育网
所以,所以,从而
所以,令,所以或…………8分
列表讨论如下:列表讨论如下:
0 2
+ — 0 — + 0 + —
0
所以当时,若,则
当时,若,则
从而 或即或
所以存在实数,满足题目要求。
21世纪教育网
同课章节目录
