24.3.2 圆内接四边形 课件(共16张PPT)
文档属性
| 名称 | 24.3.2 圆内接四边形 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 19:31:43 | ||
图片预览





文档简介
(共16张PPT)
第24章 圆
24.3 圆周角
课时2 圆内接四边形
1.理解圆内接多边形的概念.
2.掌握圆内接四边形的性质,并能够运用其进行简单的计算与证明. (重难点)
学习目标
新课导入
情境导入
如图是一个圆形笑脸,给你一个三角板,你有办法确定这个圆形笑脸的圆心吗?
O
A
C
B
D
E
O
A
C
B
D
α
β
新课讲解
知识点1 圆内接四边形的概念和性质
合作探究
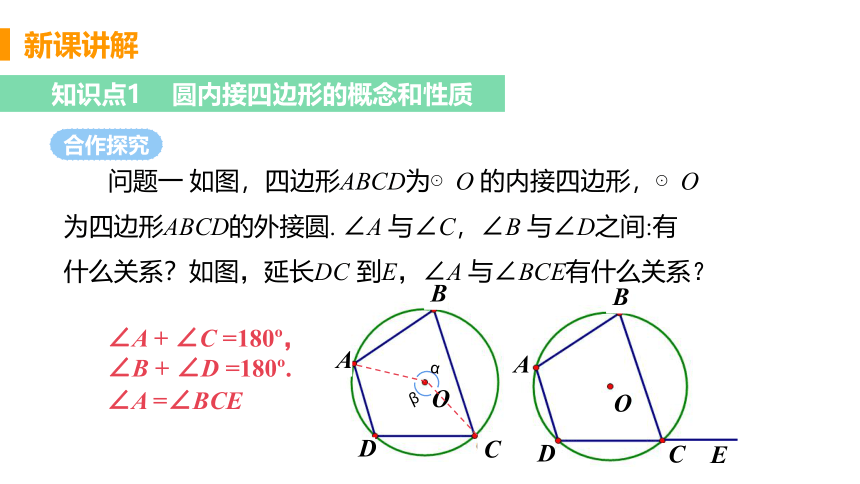
问题一 如图,四边形ABCD为⊙O 的内接四边形,⊙O为四边形ABCD的外接圆. ∠A 与∠C,∠B 与∠D之间:有什么关系?如图,延长DC 到E,∠A 与∠BCE有什么关系?
∠A + ∠C =180 ,
∠B + ∠D =180 .
∠A =∠BCE
O
A
C
B
D
E
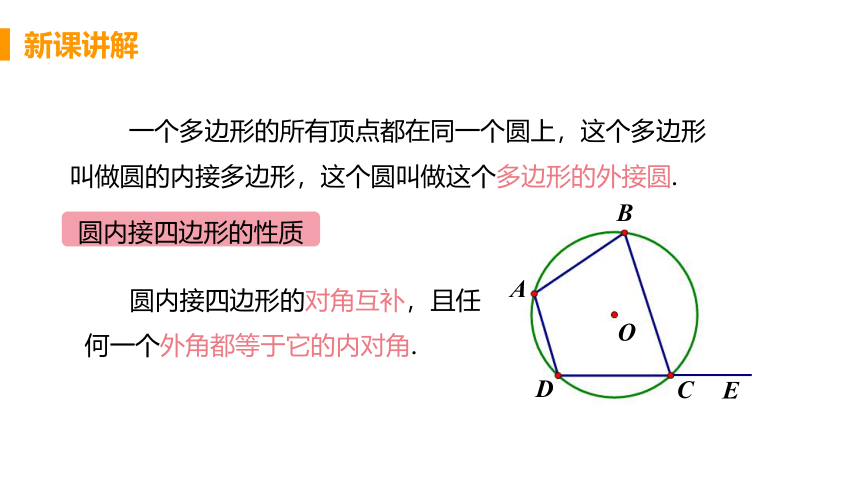
一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆的内接多边形,这个圆叫做这个多边形的外接圆.
新课讲解
圆内接四边形的性质
圆内接四边形的对角互补,且任
何一个外角都等于它的内对角.
新课讲解
例
典例分析
1 在圆内接四边形ABCD中, ∠A、 ∠B、 ∠C的度数之比是2:3:6,求这个四边形各角的度数.
解:设∠A、 ∠B、 ∠C的度数分别等于2x°、3x°、6x°.
∵四边形ABCD内接于圆,
∴ ∠A+ ∠C = ∠B+ ∠D =180°.
∵2x+6x=180, ∴x=22.5.
∴ ∠A=45°, ∠B=67.5°, ∠C=135°,
∠D=180° - 67.5°=112.5°.
新课讲解
例
2 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G. 求证:∠FGD=∠ADC.
证明:∵四边形ACDG内接于⊙O,
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
新课讲解
练一练
1
2
下列说法正确的是( )
A.在圆内部的多边形叫做圆内接多边形
B.过四边形的四个顶点的圆叫做这个四边形的外接圆
C.任意一个四边形都有外接圆
D.一个圆只有唯一一个内接四边形
下列多边形中一定有外接圆的是( )
A.三角形 B.四边形
C.五边形 D.六边形
B
A
新课讲解
3
如图所示,P是等边三角形ABC外接圆的弧BC上一点,CP
的延长线和AB的延长线相交于D点,连接BP.
求证:(1)∠D=∠CBP;
(2)AC2=CP·CD.
解:(1)∵△ABC为等边三角形,
∴∠A=∠ABC=60°.
∴∠DBC=180°-∠ABC=120°.
∵四边形ABPC为圆内接四边形,
∴∠A+∠BPC=180°.∴∠BPC=120°.
∴∠DBC=∠BPC.
又∵∠BCP=∠DCB,∴△BPC∽△DBC.∴∠D=∠CBP.
(2)由(1)知△BPC∽△DBC,∴ .又∵在等边三角
形ABC中,AC=BC,∴AC2=CP·CD.
新课讲解
课堂小结
一个多边形所有顶点都在同一个圆上,这个多边形叫作圆的内接多边形,这个圆叫做这个多边形的外接圆.
圆内接四边形的对角互补,且任何一个外角都等于它的内对角.
圆内接四边形
定义
定理
当堂小练
1 圆内接四边形ABCD中,若∠A=70°,则∠C 等于( )
A.20° B.30° C.70° D.110°
2 下列命题:①圆内接平行四边形是矩形;②圆内接矩形是正方形;③圆内接菱形是正方形;④任意四边形一定有外接圆.其中真命题有( )
A.1个 B.2个 C.3个 D.4个
D
B
当堂小练
3.⊙O的内接四边形ABCD中,∠A∶∠B∶∠C=1∶2∶3 ,则∠D= .
90
4.如图,圆内接四边形ABCD的两组对边的延长线分别相交于点E,F,若∠A=55°,∠E=30°,则∠F= °.
40
3. 如图,四边形ABCD内接于☉O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.求证:DB=DC.
证明:∵∠DAC与∠DBC是同弧所对的圆周角,
∴∠DAC=∠DBC.
∵AD平分∠CAE,∴∠EAD=∠DAC,
∴∠EAD=∠DBC.
∵四边形ABCD内接于☉O,
∴∠EAD=∠BCD,∠DBC=∠BCD,
∴DB=DC.
当堂小练
D
拓展与延伸
7. 已知:如图,两个等圆⊙O1和⊙O2相交于A,B两点,经过点A的直线与两圆分别交于点C、点D,经过点B的直线与两圆分别交于点E、点F.若CD∥EF,
求证:四边形CEFD是平行四边形
拓展与延伸
证明:连接AB,如图.
∵四边形ABEC是⊙O1
的内接四边形,
∴∠BAD=∠E.
又∵四边形ADFB是⊙O2的内接四边形,
∴∠BAD+∠F=180°,∴∠E+∠F=180°.
∴CE∥DF.
又∵CD∥EF,∴四边形CEFD是平行四边形.
第24章 圆
24.3 圆周角
课时2 圆内接四边形
1.理解圆内接多边形的概念.
2.掌握圆内接四边形的性质,并能够运用其进行简单的计算与证明. (重难点)
学习目标
新课导入
情境导入
如图是一个圆形笑脸,给你一个三角板,你有办法确定这个圆形笑脸的圆心吗?
O
A
C
B
D
E
O
A
C
B
D
α
β
新课讲解
知识点1 圆内接四边形的概念和性质
合作探究
问题一 如图,四边形ABCD为⊙O 的内接四边形,⊙O为四边形ABCD的外接圆. ∠A 与∠C,∠B 与∠D之间:有什么关系?如图,延长DC 到E,∠A 与∠BCE有什么关系?
∠A + ∠C =180 ,
∠B + ∠D =180 .
∠A =∠BCE
O
A
C
B
D
E
一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆的内接多边形,这个圆叫做这个多边形的外接圆.
新课讲解
圆内接四边形的性质
圆内接四边形的对角互补,且任
何一个外角都等于它的内对角.
新课讲解
例
典例分析
1 在圆内接四边形ABCD中, ∠A、 ∠B、 ∠C的度数之比是2:3:6,求这个四边形各角的度数.
解:设∠A、 ∠B、 ∠C的度数分别等于2x°、3x°、6x°.
∵四边形ABCD内接于圆,
∴ ∠A+ ∠C = ∠B+ ∠D =180°.
∵2x+6x=180, ∴x=22.5.
∴ ∠A=45°, ∠B=67.5°, ∠C=135°,
∠D=180° - 67.5°=112.5°.
新课讲解
例
2 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G. 求证:∠FGD=∠ADC.
证明:∵四边形ACDG内接于⊙O,
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
新课讲解
练一练
1
2
下列说法正确的是( )
A.在圆内部的多边形叫做圆内接多边形
B.过四边形的四个顶点的圆叫做这个四边形的外接圆
C.任意一个四边形都有外接圆
D.一个圆只有唯一一个内接四边形
下列多边形中一定有外接圆的是( )
A.三角形 B.四边形
C.五边形 D.六边形
B
A
新课讲解
3
如图所示,P是等边三角形ABC外接圆的弧BC上一点,CP
的延长线和AB的延长线相交于D点,连接BP.
求证:(1)∠D=∠CBP;
(2)AC2=CP·CD.
解:(1)∵△ABC为等边三角形,
∴∠A=∠ABC=60°.
∴∠DBC=180°-∠ABC=120°.
∵四边形ABPC为圆内接四边形,
∴∠A+∠BPC=180°.∴∠BPC=120°.
∴∠DBC=∠BPC.
又∵∠BCP=∠DCB,∴△BPC∽△DBC.∴∠D=∠CBP.
(2)由(1)知△BPC∽△DBC,∴ .又∵在等边三角
形ABC中,AC=BC,∴AC2=CP·CD.
新课讲解
课堂小结
一个多边形所有顶点都在同一个圆上,这个多边形叫作圆的内接多边形,这个圆叫做这个多边形的外接圆.
圆内接四边形的对角互补,且任何一个外角都等于它的内对角.
圆内接四边形
定义
定理
当堂小练
1 圆内接四边形ABCD中,若∠A=70°,则∠C 等于( )
A.20° B.30° C.70° D.110°
2 下列命题:①圆内接平行四边形是矩形;②圆内接矩形是正方形;③圆内接菱形是正方形;④任意四边形一定有外接圆.其中真命题有( )
A.1个 B.2个 C.3个 D.4个
D
B
当堂小练
3.⊙O的内接四边形ABCD中,∠A∶∠B∶∠C=1∶2∶3 ,则∠D= .
90
4.如图,圆内接四边形ABCD的两组对边的延长线分别相交于点E,F,若∠A=55°,∠E=30°,则∠F= °.
40
3. 如图,四边形ABCD内接于☉O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.求证:DB=DC.
证明:∵∠DAC与∠DBC是同弧所对的圆周角,
∴∠DAC=∠DBC.
∵AD平分∠CAE,∴∠EAD=∠DAC,
∴∠EAD=∠DBC.
∵四边形ABCD内接于☉O,
∴∠EAD=∠BCD,∠DBC=∠BCD,
∴DB=DC.
当堂小练
D
拓展与延伸
7. 已知:如图,两个等圆⊙O1和⊙O2相交于A,B两点,经过点A的直线与两圆分别交于点C、点D,经过点B的直线与两圆分别交于点E、点F.若CD∥EF,
求证:四边形CEFD是平行四边形
拓展与延伸
证明:连接AB,如图.
∵四边形ABEC是⊙O1
的内接四边形,
∴∠BAD=∠E.
又∵四边形ADFB是⊙O2的内接四边形,
∴∠BAD+∠F=180°,∴∠E+∠F=180°.
∴CE∥DF.
又∵CD∥EF,∴四边形CEFD是平行四边形.
