24.4.1-24.4.2直线与圆的位置关系&切线的性质与判定 课件(共32张PPT)
文档属性
| 名称 | 24.4.1-24.4.2直线与圆的位置关系&切线的性质与判定 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 528.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
第24章 圆
24.4 直线与圆的位置关系
课时1 直线与圆的位置关系
切线长性质与判定
1.理解直线和圆的三种位置关系的定义.
2.掌握用数量关系判定直线和圆的位置关系的方法.(重点)
3.使学生掌握圆的切线的判定方法和切线的性质;能够运用切线的判定方法证明直线是圆的切线.(难点)
学习目标
新课导入
情境导入
你看过日出吗,如图是海上日出的一组图片,如果把海平面看做一条直线,太阳看做一个圆,在日出过程中,二者会出现几种位置关系呢?
新课讲解
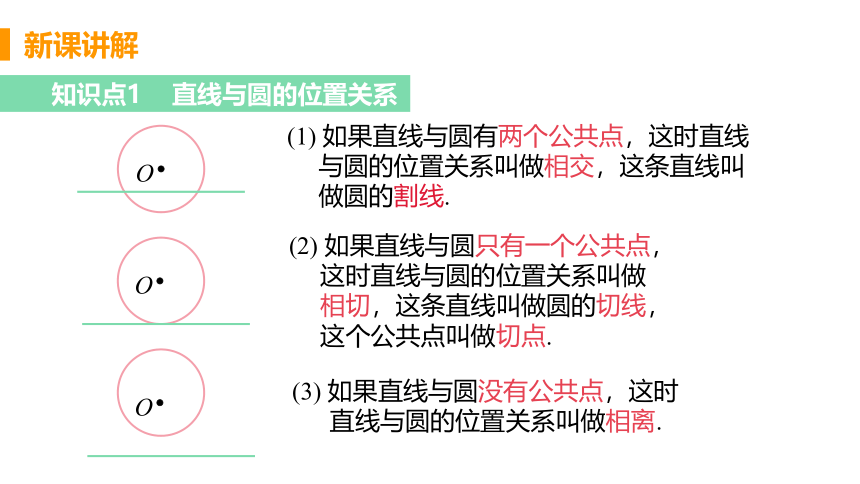
知识点1 直线与圆的位置关系
(2) 如果直线与圆只有一个公共点,
这时直线与圆的位置关系叫做
相切,这条直线叫做圆的切线,
这个公共点叫做切点.
(3) 如果直线与圆没有公共点,这时
直线与圆的位置关系叫做相离.
O
O
O
(1) 如果直线与圆有两个公共点,这时直线
与圆的位置关系叫做相交,这条直线叫
做圆的割线.
新课导入
d>r 直线l与⊙O相离
d=r 直线l与⊙O相切
dr
r
r
新课讲解
例
典例分析
1 如图 , Rt△ABC 的斜边 AB= 10 cm,∠A =30°.
(1)以点C为圆心作圆,当半径为多少时,AB与⊙C 相切?
(2)以点C为圆心、半径r分别为4 cm和5 cm作两个圆,这两个
圆与斜边AB分别有怎样的位置关系?
A
C
B
┐
新课讲解
A
C
B
┐
D
解:(1)过点C作边AB上的高CD.
∵∠A=30°,AB=10cm,
当半径为 时,AB与☉C相切.
∴∠B=60°,
在Rt△BCD中,有
当r =4cm时,d>r,⊙C与AB相离;
当r =5cm时,d<r,⊙C与AB相交.
(2)由 (1) 可知圆心 C 到 AB 的距离
新课讲解
练一练
1
2
在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.5 cm为半径画圆,则⊙C与直线AB的位置关系是( )
A.相交 B.相切
C.相离 D.不能确定
A
如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
A.2.3 B.2.4
C.2.5 D.2.6
B
新课讲解
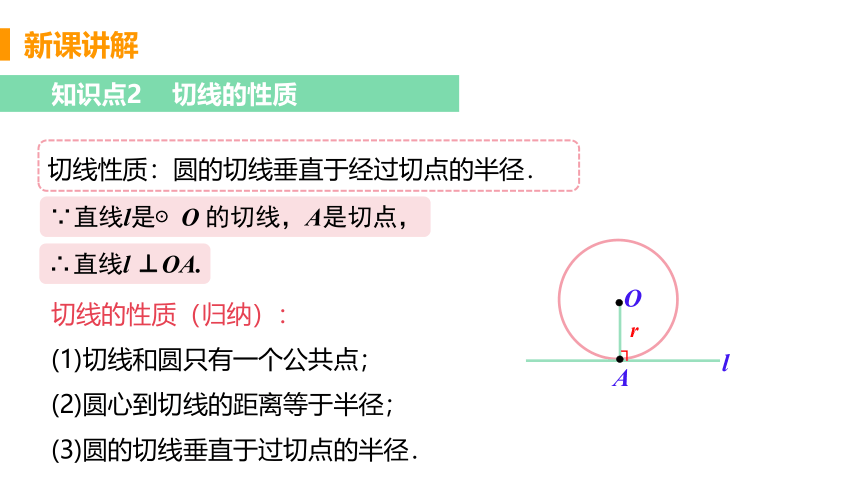
知识点2 切线的性质
切线性质:圆的切线垂直于经过切点的半径.
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
A
l
O
r
┐
切线的性质(归纳):
(1)切线和圆只有一个公共点;
(2)圆心到切线的距离等于半径;
(3)圆的切线垂直于过切点的半径.
新课讲解
例
典例分析
2 如图,PA为⊙O的切线,切点为A,OP = 2,
∠APO=30° ,求⊙O的半径.
解:连接OA,则OA为⊙O的半径,
因为PA是⊙O的切线,所以OA⊥AP,
又∠APO=30°,OP=2,
所以OA= OP=1,即⊙O的半径为1.
新课讲解
练一练
1
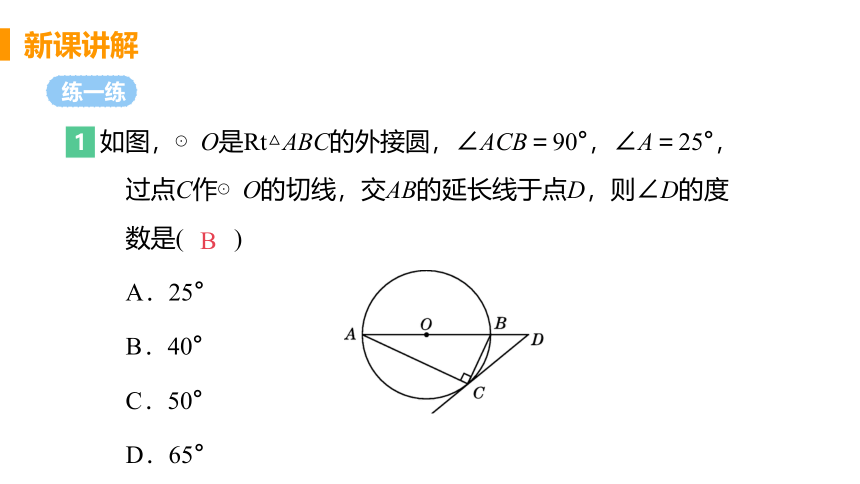
如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
A.25°
B.40°
C.50°
D.65°
B
新课讲解
2
如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于
点D,若∠C=70°,则∠AOD的度数为( )
A.70°
B.35°
C.20°
D.40°
D
新课讲解
3
如图,AB是⊙O的直径,P为AB延长线上任意一点,C为半
圆ACB的中点,PD切⊙O于点D,连接CD交AB于点E.
求证:PD=PE.
分析:要证PD=PE,需证∠PDE
=∠PED,而题目缺少直
接证明这两个角相等的条件,因此
需证其余角相等,所以要构造出它们
的余角的基本图形,需作出相应的辅助线.
证明:如图,连接OC,OD.
∵PD为⊙O的切线,
且C为半圆ACB的中点,
∴OD⊥PD,OC⊥AB.
∴∠PDE=∠PDO-∠ODE=90°-∠ODE,
∠PED=∠CEO=90°-∠C.
又∵OC=OD,∴∠C=∠ODE,
∴∠PDE=∠PED. ∴PD=PE.
新课讲解
新课讲解
知识点3 切线的判定定理
问题一 已知⊙O上一点P,怎样根据圆的切线定义过点 P作⊙O的切线?
作法:1. 连接OP.
2. 过点 P 作直线 l⊥OP.
则直线 l 即为所作.
P
l
O
合作探究
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的判定定理:
应用格式
OA为⊙O的半径
l ⊥ OA于A
l为⊙O的切线
A
l
O
新课讲解
新课讲解
切线的判定方法有三种:
①定义法:直线与圆有唯一公共点;
②数量法:圆心到直线的距离等于该圆的半径;
③切线的判定定理:经过半径的外端并且垂直这条
半径的直线是圆的切线.
l
l
r
d
A
l
O
新课讲解
1 如图,已知AB为⊙O的直径,点D在AB的延长线 上,
BD=OB,点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.
例
典例分析
新课讲解
证明:如图,连接OC,BC.
∵AB为⊙O的直径,
∴∠ACB=90°.
∵∠CAB=30°,
∴BC= AB=OB.
又∵BD=OB,
∴BC=BD=OB= OD,
∴∠OCD=90°.
∴DC是⊙O的切线.
新课讲解
练一练
1
2
如图,在△ABC中,AB=AC,∠B= 30°,
以点A为圆心,以3 cm为半径作⊙A,当AB =
_____cm时,BC与⊙A相切.
如图,已知AB为⊙O的直径,点D在AB的
延长线上,BD=OB,点C在圆上,∠CAB
=30°. 求证:DC是⊙O的切线.
6
分析:因为点C在圆上,所以连接OC,
证明OC⊥CD,而要证OC⊥CD,
只需证△OCD为直角三角形.
证明:如图,连接OC,BC.
∵AB为⊙O的直径,∴∠ACB=90°.
∵∠CAB=30°,∴BC= AB=OB.
又∵BD=OB,∴BC=BD=OB= OD,
∴∠OCD=90°.
∴DC是⊙O的切线.
新课讲解
课堂小结
(d< r)
(d= r)
(d> r)
直线与圆没有公共点
直线与圆有唯一公共点
直线与圆有两个公共点
直线和圆的位置关系
相离
相切
相交
切线的
性质
有1个公共点
d=r
性质定理
圆的切线垂直于经过切点的半径
有切线时常用辅助线
见切线,连切点,得垂直.
课堂小结
切线的
判定方法
数量关系法
判定定理
1个公共点,则相切
d=r,则相切
经过半径的外端并且垂直于这条半径的直线是圆的切线
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
定义法
课堂小结
当堂小练
1.如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆
心的圆与AB相切,则☉C的半径为( )
A.2.3 B.2.4 C.2.5 D.2.6
B
2. 如图,△ABC的边AC与☉O相交于点D,C,且经过圆心O,边AB与
☉O相切,切点为B.如果∠C=28°,那么∠A的度数为 .
34o
当堂小练
3. 如图,已知AB为☉O的直径,CD,CB为☉O
的两条切线,切点分别为D,B,连接AD.
求证:AD//OC.
证明:如图,连接OD.
∵CD,CB为☉O的两条切线,
∴OD⊥CD,OB⊥CB,
∴∠ODC=∠OBC=90°.
又∵OD=OB,OC=OC,
∴Rt△COD≌Rt△COB,
∴∠BOD=2∠BOC.
∵OA=OD,∴∠ODA=∠A.
∵AB为☉O的直径,∠BOD是△AOD的外角,
∴∠BOD=∠ODA+∠A=2∠A.
∴∠BOC=∠A,
∴AD//OC.
当堂小练
当堂小练
4. 如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作
OD∥BC与过点A的切线交于点D,连接DC并延长交AB的
延长线于点E. 求证:DE是⊙O的切线.
分析:连接OC,已知DA是⊙O的切线,则∠DAO=90°,要证∠DCO=90°,只需证明△DAO与△DCO全等即可.
当堂小练
证明:如图,连接OC.
∵AD是过点A的切线,AB是⊙O的直径,
∴AD⊥AB,∴∠DAB=90°.
∵OD∥BC,∴∠1=∠2,∠3=∠4.
∵OC=OB,∴∠2=∠4.∴∠1=∠3.
在△COD和△AOD中,
∴∠OCD=∠DAB=90°,即OC⊥DE于点C.
∵OC是⊙O的半径,∴DE是⊙O的切线.
D
拓展与延伸
1.如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN
直线AB于M,交直线AC于N,连接DB,CD.
(1)求证:AE·DE=BE·CE;
(2)若MN∥BC,试探究BD与CD之间的数量关系;
(3)在(2)的条件下,已知AB=6,AN=15,求AD的长.
拓展与延伸
(1)证明:∵∠ABC=∠ADC,∠1=∠3,
∴△ABE∽△CDE, ∴ ,
∴AE·DE=BE·CE.
(2)解:连接OD,如图,
∵MN切⊙O于点D,
∴OD⊥MN,
∵MN∥BC,∴OD⊥BC,
∴在⊙O中, ,∴BD=CD.
拓展与延伸
(3)解:∵BC∥MN,∴∠4=∠ANM.
又∵∠4=∠ADB,
∴∠ADB=∠AND.
由(2)知 ,
∴∠1=∠2.∴△ADB∽△AND.
∴ ,
即
第24章 圆
24.4 直线与圆的位置关系
课时1 直线与圆的位置关系
切线长性质与判定
1.理解直线和圆的三种位置关系的定义.
2.掌握用数量关系判定直线和圆的位置关系的方法.(重点)
3.使学生掌握圆的切线的判定方法和切线的性质;能够运用切线的判定方法证明直线是圆的切线.(难点)
学习目标
新课导入
情境导入
你看过日出吗,如图是海上日出的一组图片,如果把海平面看做一条直线,太阳看做一个圆,在日出过程中,二者会出现几种位置关系呢?
新课讲解
知识点1 直线与圆的位置关系
(2) 如果直线与圆只有一个公共点,
这时直线与圆的位置关系叫做
相切,这条直线叫做圆的切线,
这个公共点叫做切点.
(3) 如果直线与圆没有公共点,这时
直线与圆的位置关系叫做相离.
O
O
O
(1) 如果直线与圆有两个公共点,这时直线
与圆的位置关系叫做相交,这条直线叫
做圆的割线.
新课导入
d>r 直线l与⊙O相离
d=r 直线l与⊙O相切
d
r
r
新课讲解
例
典例分析
1 如图 , Rt△ABC 的斜边 AB= 10 cm,∠A =30°.
(1)以点C为圆心作圆,当半径为多少时,AB与⊙C 相切?
(2)以点C为圆心、半径r分别为4 cm和5 cm作两个圆,这两个
圆与斜边AB分别有怎样的位置关系?
A
C
B
┐
新课讲解
A
C
B
┐
D
解:(1)过点C作边AB上的高CD.
∵∠A=30°,AB=10cm,
当半径为 时,AB与☉C相切.
∴∠B=60°,
在Rt△BCD中,有
当r =4cm时,d>r,⊙C与AB相离;
当r =5cm时,d<r,⊙C与AB相交.
(2)由 (1) 可知圆心 C 到 AB 的距离
新课讲解
练一练
1
2
在Rt△ABC中,∠C=90°,BC=3 cm,AC=4 cm,以点C为圆心,以2.5 cm为半径画圆,则⊙C与直线AB的位置关系是( )
A.相交 B.相切
C.相离 D.不能确定
A
如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
A.2.3 B.2.4
C.2.5 D.2.6
B
新课讲解
知识点2 切线的性质
切线性质:圆的切线垂直于经过切点的半径.
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
A
l
O
r
┐
切线的性质(归纳):
(1)切线和圆只有一个公共点;
(2)圆心到切线的距离等于半径;
(3)圆的切线垂直于过切点的半径.
新课讲解
例
典例分析
2 如图,PA为⊙O的切线,切点为A,OP = 2,
∠APO=30° ,求⊙O的半径.
解:连接OA,则OA为⊙O的半径,
因为PA是⊙O的切线,所以OA⊥AP,
又∠APO=30°,OP=2,
所以OA= OP=1,即⊙O的半径为1.
新课讲解
练一练
1
如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
A.25°
B.40°
C.50°
D.65°
B
新课讲解
2
如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于
点D,若∠C=70°,则∠AOD的度数为( )
A.70°
B.35°
C.20°
D.40°
D
新课讲解
3
如图,AB是⊙O的直径,P为AB延长线上任意一点,C为半
圆ACB的中点,PD切⊙O于点D,连接CD交AB于点E.
求证:PD=PE.
分析:要证PD=PE,需证∠PDE
=∠PED,而题目缺少直
接证明这两个角相等的条件,因此
需证其余角相等,所以要构造出它们
的余角的基本图形,需作出相应的辅助线.
证明:如图,连接OC,OD.
∵PD为⊙O的切线,
且C为半圆ACB的中点,
∴OD⊥PD,OC⊥AB.
∴∠PDE=∠PDO-∠ODE=90°-∠ODE,
∠PED=∠CEO=90°-∠C.
又∵OC=OD,∴∠C=∠ODE,
∴∠PDE=∠PED. ∴PD=PE.
新课讲解
新课讲解
知识点3 切线的判定定理
问题一 已知⊙O上一点P,怎样根据圆的切线定义过点 P作⊙O的切线?
作法:1. 连接OP.
2. 过点 P 作直线 l⊥OP.
则直线 l 即为所作.
P
l
O
合作探究
经过半径的外端并且垂直于这条半径的直线是圆的切线.
切线的判定定理:
应用格式
OA为⊙O的半径
l ⊥ OA于A
l为⊙O的切线
A
l
O
新课讲解
新课讲解
切线的判定方法有三种:
①定义法:直线与圆有唯一公共点;
②数量法:圆心到直线的距离等于该圆的半径;
③切线的判定定理:经过半径的外端并且垂直这条
半径的直线是圆的切线.
l
l
r
d
A
l
O
新课讲解
1 如图,已知AB为⊙O的直径,点D在AB的延长线 上,
BD=OB,点C在圆上,∠CAB=30°.
求证:DC是⊙O的切线.
例
典例分析
新课讲解
证明:如图,连接OC,BC.
∵AB为⊙O的直径,
∴∠ACB=90°.
∵∠CAB=30°,
∴BC= AB=OB.
又∵BD=OB,
∴BC=BD=OB= OD,
∴∠OCD=90°.
∴DC是⊙O的切线.
新课讲解
练一练
1
2
如图,在△ABC中,AB=AC,∠B= 30°,
以点A为圆心,以3 cm为半径作⊙A,当AB =
_____cm时,BC与⊙A相切.
如图,已知AB为⊙O的直径,点D在AB的
延长线上,BD=OB,点C在圆上,∠CAB
=30°. 求证:DC是⊙O的切线.
6
分析:因为点C在圆上,所以连接OC,
证明OC⊥CD,而要证OC⊥CD,
只需证△OCD为直角三角形.
证明:如图,连接OC,BC.
∵AB为⊙O的直径,∴∠ACB=90°.
∵∠CAB=30°,∴BC= AB=OB.
又∵BD=OB,∴BC=BD=OB= OD,
∴∠OCD=90°.
∴DC是⊙O的切线.
新课讲解
课堂小结
(d< r)
(d= r)
(d> r)
直线与圆没有公共点
直线与圆有唯一公共点
直线与圆有两个公共点
直线和圆的位置关系
相离
相切
相交
切线的
性质
有1个公共点
d=r
性质定理
圆的切线垂直于经过切点的半径
有切线时常用辅助线
见切线,连切点,得垂直.
课堂小结
切线的
判定方法
数量关系法
判定定理
1个公共点,则相切
d=r,则相切
经过半径的外端并且垂直于这条半径的直线是圆的切线
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
定义法
课堂小结
当堂小练
1.如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆
心的圆与AB相切,则☉C的半径为( )
A.2.3 B.2.4 C.2.5 D.2.6
B
2. 如图,△ABC的边AC与☉O相交于点D,C,且经过圆心O,边AB与
☉O相切,切点为B.如果∠C=28°,那么∠A的度数为 .
34o
当堂小练
3. 如图,已知AB为☉O的直径,CD,CB为☉O
的两条切线,切点分别为D,B,连接AD.
求证:AD//OC.
证明:如图,连接OD.
∵CD,CB为☉O的两条切线,
∴OD⊥CD,OB⊥CB,
∴∠ODC=∠OBC=90°.
又∵OD=OB,OC=OC,
∴Rt△COD≌Rt△COB,
∴∠BOD=2∠BOC.
∵OA=OD,∴∠ODA=∠A.
∵AB为☉O的直径,∠BOD是△AOD的外角,
∴∠BOD=∠ODA+∠A=2∠A.
∴∠BOC=∠A,
∴AD//OC.
当堂小练
当堂小练
4. 如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作
OD∥BC与过点A的切线交于点D,连接DC并延长交AB的
延长线于点E. 求证:DE是⊙O的切线.
分析:连接OC,已知DA是⊙O的切线,则∠DAO=90°,要证∠DCO=90°,只需证明△DAO与△DCO全等即可.
当堂小练
证明:如图,连接OC.
∵AD是过点A的切线,AB是⊙O的直径,
∴AD⊥AB,∴∠DAB=90°.
∵OD∥BC,∴∠1=∠2,∠3=∠4.
∵OC=OB,∴∠2=∠4.∴∠1=∠3.
在△COD和△AOD中,
∴∠OCD=∠DAB=90°,即OC⊥DE于点C.
∵OC是⊙O的半径,∴DE是⊙O的切线.
D
拓展与延伸
1.如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN
直线AB于M,交直线AC于N,连接DB,CD.
(1)求证:AE·DE=BE·CE;
(2)若MN∥BC,试探究BD与CD之间的数量关系;
(3)在(2)的条件下,已知AB=6,AN=15,求AD的长.
拓展与延伸
(1)证明:∵∠ABC=∠ADC,∠1=∠3,
∴△ABE∽△CDE, ∴ ,
∴AE·DE=BE·CE.
(2)解:连接OD,如图,
∵MN切⊙O于点D,
∴OD⊥MN,
∵MN∥BC,∴OD⊥BC,
∴在⊙O中, ,∴BD=CD.
拓展与延伸
(3)解:∵BC∥MN,∴∠4=∠ANM.
又∵∠4=∠ADB,
∴∠ADB=∠AND.
由(2)知 ,
∴∠1=∠2.∴△ADB∽△AND.
∴ ,
即
