24.4.3 切线长定理 课件(共18张PPT)
文档属性
| 名称 | 24.4.3 切线长定理 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 241.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 18:17:46 | ||
图片预览




文档简介
(共18张PPT)
第24章 圆
24.4 直线与圆的位置关系
课时2 切线长定理
1.掌握切线长定理及其应用.(重点)
2.学会与切线长定理有关的计算和证明问题. (难点)
学习目标
新课导入
情境导入
新农村建设中,张村计划在一个三角形中建一个最大面积的圆形花园,请你设计一个建筑方案.
新课讲解
知识点1 切线长定理
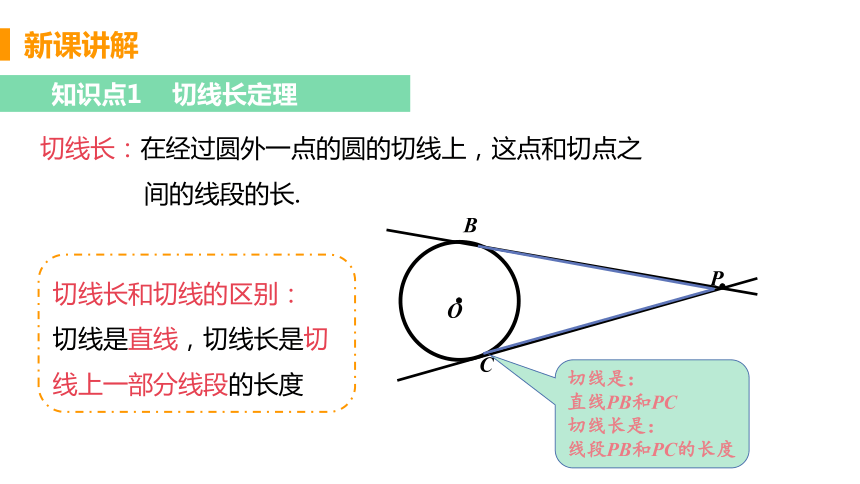
切线长:在经过圆外一点的圆的切线上,这点和切点之
间的线段的长.
P
B
C
O
切线长和切线的区别:
切线是直线,切线长是切线上一部分线段的长度
切线是:
直线PB和PC
切线长是:
线段PB和PC的长度
新课讲解
O.
P
A
B
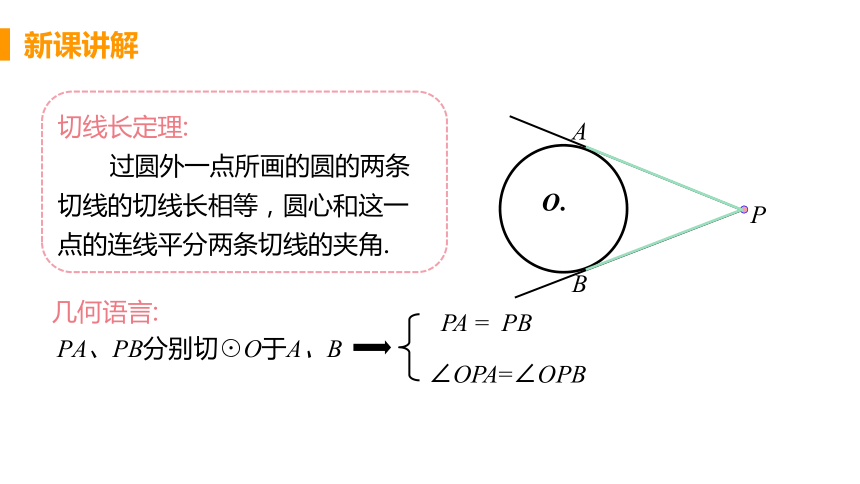
切线长定理:
过圆外一点所画的圆的两条切线的切线长相等,圆心和这一点的连线平分两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
B
P
O
A
C
E
D
(1)图中所有的垂直关系:
(2)图中与∠OAC和∠AOC相等的角:
(3)图中所有的相等的线段:
(4)图中所有的全等三角形:
(5)图中所有的等腰三角形:
新课讲解
PA、PB是☉O的两条切线,A、B为切点,直线OP交☉O于点D、E,交AB于C.
OA⊥PA,OB ⊥PB,AB ⊥OP.
∠OAC=∠OBC=∠APC=∠BPC.
∠AOC=∠BOC=∠PAC=∠PBC
PA=PB,AC =BC,OA =OB.
△AOP ≌ △BOP,
△AOC ≌ △BOC,
△ACP ≌ △BCP.
△ABP △AOB
新课讲解
例
典例分析
1 已知:如图,四边形ABCD的边AB,BC,CD,DA和⊙O分别相切于点E,F,G,H. 求证: AB + CD = DA + BC.
证明:∵ AB,BC,CD,DA都与⊙O相切,
E,F,G,H是切点,
∴AE = AH,BE = BF,CG = CF,DG = DH.
∴AE + BE + CG + DG = AH + BF + CF + DH,
即 AB + CD = DA + BC.
·
A
B
C
D
O
E
F
G
H
2 如图,PA,PB是⊙O的切线,切点分别为
A,B,BC为⊙O的直径,连接AB,AC,OP.
求证:(1)∠APB=2∠ABC;(2)AC∥OP.
新课讲解
分析:(1)由切线长定理知∠BPO=∠APO= ∠APB,
而要证∠APB=2∠ABC,即证明∠ABC=
∠APB=∠BPO,利用同角的余角相等可证;
(2)证明AC∥OP,可用AC⊥AB,OP⊥AB,也可
用同位角相等两直线平行来证.
例
新课讲解
解:(1)∵PA,PB分别切⊙O于点A,B,
∴由切线长定理知∠APO=∠BPO= ∠APB,PA=PB,
∴PO⊥AB,∴∠ABP+∠BPO=90°.
又∵PB是⊙O的切线,∴OB⊥PB.
∴∠ABP+∠ABC=90°.
∴∠ABC=∠BPO= ∠APB,
即∠APB=2∠ABC.
(2)∵BC是⊙O的直径,∴∠BAC=90°,
即AC⊥AB.由(1)知OP⊥AB,∴AC∥OP.
新课讲解
练一练
1
2
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.4 D.8
如图,PA和PB是⊙O的切线,点A和B是 切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60° B.65° C.70° D.75°
B
C
新课讲解
如图,PA,PB是⊙O的切线,A,B是切点,点C是AB 上一点,过点C作⊙O的切线分别交PA,PB于点D,E.已知∠APB=60°,⊙O的半径为 ,则△PDE的周长为____,∠DOE的度数为____.
⌒
60°
6
3
课堂小结
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
当堂小练
1. 如图,PA切⊙O于A,PB切⊙O于B,连接OP,AB.下列结论不一定正确的是( )
A.PA=PB B.OP垂直平分AB
C.∠OPA=∠OPB D.PA=AB
2.如下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
D
C
当堂小练
3. 如图,过☉O外一点P作圆的切线PA,PB,F是劣弧AB上任意一点,过点F作☉O的切线分别交PA,PB于点D,E,如果PA=10,∠P=42°.
求:(1)△PED的周长; (2)∠DOE的度数.
解:(1)∵DA,DF分别切☉O于点A,F,
∴DA=DF. 同理EF=EB,PB=PA=10.
∴△PED的周长为PD+PE+DE
=PD+PE+DF+EF=PD+PE+DA+EB
=(PD+DA)+(PE+EB)=PA+PB=20.
当堂小练
(2)∵DA,DF分别切☉O于点A,F,∴∠DAO=∠DFO=90°.
在Rt△AOD与Rt△FOD中,
∵AO=FO,OD=OD, ∴Rt△AOD≌Rt△FOD,
∴∠AOD=∠FOD = ∠AOF,
同理∠EOF=∠BOE= ∠BOF,
∴∠DOE=∠FOD+∠EOF= ∠AOF+ ∠BOF
= (∠AOF+∠BOF)= ∠AOB.又∠PAO=∠PBO=90°,
∴∠AOB=360°-∠PAO-∠PBO-∠P=180°-∠P=138°,
∴∠DOE= ∠AOB=69°.
D
拓展与延伸
1.已知在⊙O中,AC为直径,MA,MB分别切⊙O于点A,B.
(1)如图(1),若∠BAC=25°,求∠AMB的大小;
(2)如图(2),过点B作BD⊥AC于点E,交⊙O于点 D,若BD=MA,求∠AMB的大小.
拓展与延伸
解:(1)∵MA,MB分别切⊙O于点A,B,
∴MA=MB,∠OAM=90°,
∴∠MAB=∠MBA.
又∵∠OAB=25°,
∴∠MAB=90°-∠OAB
=90°-25°=65°.
∴∠AMB=180°-2∠MAB
=180°-2×65°=50°.
(2)如图 (2),过点B作BH⊥AM于点H,
∵直径AC⊥BD,MA是⊙O的切线,
∴BE= BD,四边形BHAE是矩形,
∴HA=BE= BD.
又∵BD=MA,MA=MB,
∴MH= MB.
在Rt△MBH中,∵MH= MB,
∴∠MBH=30°,∴∠AMB=60°.
拓展与延伸
第24章 圆
24.4 直线与圆的位置关系
课时2 切线长定理
1.掌握切线长定理及其应用.(重点)
2.学会与切线长定理有关的计算和证明问题. (难点)
学习目标
新课导入
情境导入
新农村建设中,张村计划在一个三角形中建一个最大面积的圆形花园,请你设计一个建筑方案.
新课讲解
知识点1 切线长定理
切线长:在经过圆外一点的圆的切线上,这点和切点之
间的线段的长.
P
B
C
O
切线长和切线的区别:
切线是直线,切线长是切线上一部分线段的长度
切线是:
直线PB和PC
切线长是:
线段PB和PC的长度
新课讲解
O.
P
A
B
切线长定理:
过圆外一点所画的圆的两条切线的切线长相等,圆心和这一点的连线平分两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
B
P
O
A
C
E
D
(1)图中所有的垂直关系:
(2)图中与∠OAC和∠AOC相等的角:
(3)图中所有的相等的线段:
(4)图中所有的全等三角形:
(5)图中所有的等腰三角形:
新课讲解
PA、PB是☉O的两条切线,A、B为切点,直线OP交☉O于点D、E,交AB于C.
OA⊥PA,OB ⊥PB,AB ⊥OP.
∠OAC=∠OBC=∠APC=∠BPC.
∠AOC=∠BOC=∠PAC=∠PBC
PA=PB,AC =BC,OA =OB.
△AOP ≌ △BOP,
△AOC ≌ △BOC,
△ACP ≌ △BCP.
△ABP △AOB
新课讲解
例
典例分析
1 已知:如图,四边形ABCD的边AB,BC,CD,DA和⊙O分别相切于点E,F,G,H. 求证: AB + CD = DA + BC.
证明:∵ AB,BC,CD,DA都与⊙O相切,
E,F,G,H是切点,
∴AE = AH,BE = BF,CG = CF,DG = DH.
∴AE + BE + CG + DG = AH + BF + CF + DH,
即 AB + CD = DA + BC.
·
A
B
C
D
O
E
F
G
H
2 如图,PA,PB是⊙O的切线,切点分别为
A,B,BC为⊙O的直径,连接AB,AC,OP.
求证:(1)∠APB=2∠ABC;(2)AC∥OP.
新课讲解
分析:(1)由切线长定理知∠BPO=∠APO= ∠APB,
而要证∠APB=2∠ABC,即证明∠ABC=
∠APB=∠BPO,利用同角的余角相等可证;
(2)证明AC∥OP,可用AC⊥AB,OP⊥AB,也可
用同位角相等两直线平行来证.
例
新课讲解
解:(1)∵PA,PB分别切⊙O于点A,B,
∴由切线长定理知∠APO=∠BPO= ∠APB,PA=PB,
∴PO⊥AB,∴∠ABP+∠BPO=90°.
又∵PB是⊙O的切线,∴OB⊥PB.
∴∠ABP+∠ABC=90°.
∴∠ABC=∠BPO= ∠APB,
即∠APB=2∠ABC.
(2)∵BC是⊙O的直径,∴∠BAC=90°,
即AC⊥AB.由(1)知OP⊥AB,∴AC∥OP.
新课讲解
练一练
1
2
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.4 D.8
如图,PA和PB是⊙O的切线,点A和B是 切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60° B.65° C.70° D.75°
B
C
新课讲解
如图,PA,PB是⊙O的切线,A,B是切点,点C是AB 上一点,过点C作⊙O的切线分别交PA,PB于点D,E.已知∠APB=60°,⊙O的半径为 ,则△PDE的周长为____,∠DOE的度数为____.
⌒
60°
6
3
课堂小结
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
当堂小练
1. 如图,PA切⊙O于A,PB切⊙O于B,连接OP,AB.下列结论不一定正确的是( )
A.PA=PB B.OP垂直平分AB
C.∠OPA=∠OPB D.PA=AB
2.如下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
D
C
当堂小练
3. 如图,过☉O外一点P作圆的切线PA,PB,F是劣弧AB上任意一点,过点F作☉O的切线分别交PA,PB于点D,E,如果PA=10,∠P=42°.
求:(1)△PED的周长; (2)∠DOE的度数.
解:(1)∵DA,DF分别切☉O于点A,F,
∴DA=DF. 同理EF=EB,PB=PA=10.
∴△PED的周长为PD+PE+DE
=PD+PE+DF+EF=PD+PE+DA+EB
=(PD+DA)+(PE+EB)=PA+PB=20.
当堂小练
(2)∵DA,DF分别切☉O于点A,F,∴∠DAO=∠DFO=90°.
在Rt△AOD与Rt△FOD中,
∵AO=FO,OD=OD, ∴Rt△AOD≌Rt△FOD,
∴∠AOD=∠FOD = ∠AOF,
同理∠EOF=∠BOE= ∠BOF,
∴∠DOE=∠FOD+∠EOF= ∠AOF+ ∠BOF
= (∠AOF+∠BOF)= ∠AOB.又∠PAO=∠PBO=90°,
∴∠AOB=360°-∠PAO-∠PBO-∠P=180°-∠P=138°,
∴∠DOE= ∠AOB=69°.
D
拓展与延伸
1.已知在⊙O中,AC为直径,MA,MB分别切⊙O于点A,B.
(1)如图(1),若∠BAC=25°,求∠AMB的大小;
(2)如图(2),过点B作BD⊥AC于点E,交⊙O于点 D,若BD=MA,求∠AMB的大小.
拓展与延伸
解:(1)∵MA,MB分别切⊙O于点A,B,
∴MA=MB,∠OAM=90°,
∴∠MAB=∠MBA.
又∵∠OAB=25°,
∴∠MAB=90°-∠OAB
=90°-25°=65°.
∴∠AMB=180°-2∠MAB
=180°-2×65°=50°.
(2)如图 (2),过点B作BH⊥AM于点H,
∵直径AC⊥BD,MA是⊙O的切线,
∴BE= BD,四边形BHAE是矩形,
∴HA=BE= BD.
又∵BD=MA,MA=MB,
∴MH= MB.
在Rt△MBH中,∵MH= MB,
∴∠MBH=30°,∴∠AMB=60°.
拓展与延伸
