24.6.1 正多边形和圆 课件(共19张PPT)
文档属性
| 名称 | 24.6.1 正多边形和圆 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 269.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 18:14:15 | ||
图片预览




文档简介
(共19张PPT)
第24章 圆
24.6 正多边形与圆
课时1 正多边形与圆
1.理解并掌握正多边形和圆的有关概念,并能进行相关计算.(重难点)
2.学会通过等分圆周的方法作正多边形.
学习目标
新课导入
情境导入
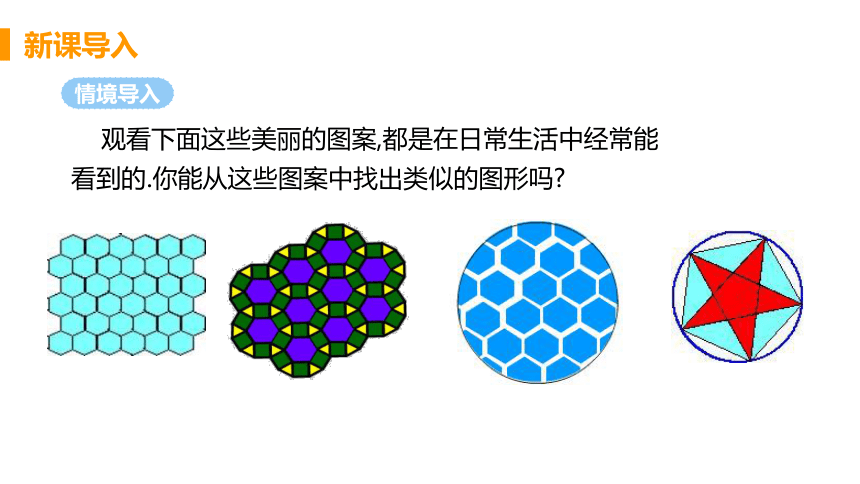
观看下面这些美丽的图案,都是在日常生活中经常能看到的.你能从这些图案中找出类似的图形吗
新课讲解
知识点1 正多边形的概念
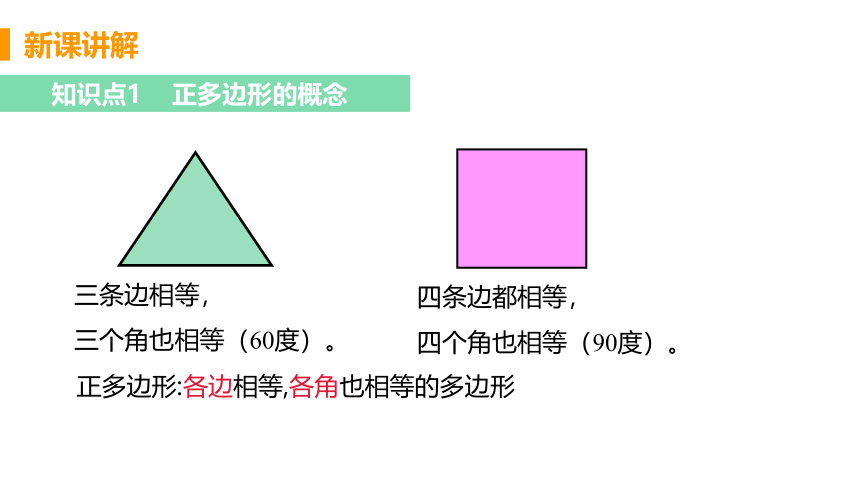
正多边形:各边相等,各角也相等的多边形
三条边相等,
三个角也相等(60度)。
四条边都相等,
四个角也相等(90度)。
新课讲解
例
典例分析
1 下列说法不正确的是( )
A.等边三角形是正多边形
B.各边相等,各角相等的多边形是正多边形
C.菱形不一定是正多边形
D.各角相等的多边形是正多边形
解析:等边三角形是正三角形;当菱形的四角相等时
才是正多边 形(正方形),所以菱形不一定是正多边形;
各边相等,各角相等的多边形是正多边形,故D不对.
D
新课讲解
练一练
1
2
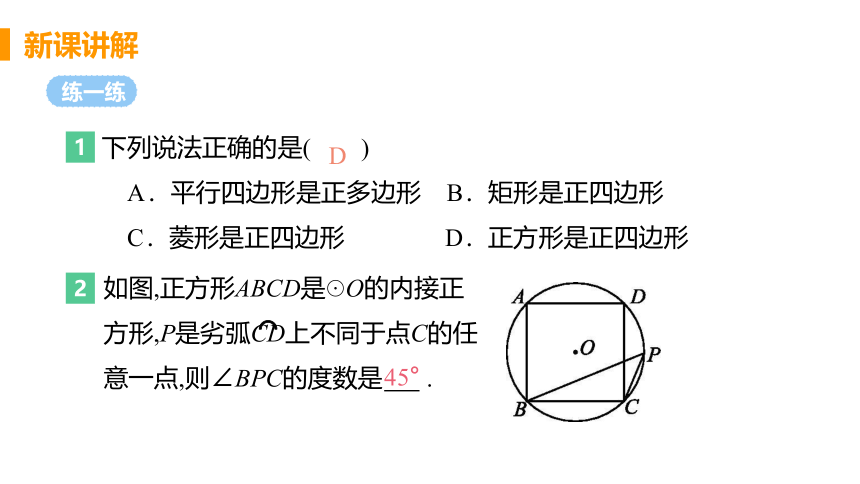
下列说法正确的是( )
A.平行四边形是正多边形 B.矩形是正四边形
C.菱形是正四边形 D.正方形是正四边形
⌒
D
45°
如图,正方形ABCD是☉O的内接正
方形,P是劣弧CD上不同于点C的任
意一点,则∠BPC的度数是 .
新课讲解
知识点2 利用圆画正多边形
问题一 如图,把☉O进行5等分,依次连接各等分点得到五边形ABCDE .分别过点A,B,C,D,E作☉O的切线,切线交于点P,Q,R,S,T,依次连接各交点。得到五边形PQRST.
(1)五边形ABCDE是正多边形吗?
(2)五边形PQRST是正多边形吗?
合作探究
新课讲解
证明(1):如图,把⊙O分成相等的5段弧,
依次连接各分点得到五边形ABCDE.
·
A
O
E
D
C
B
⌒
⌒
⌒
⌒
⌒
∵AB=BC=CD=DE=EA,
⌒
⌒
⌒
∴AB=BC=CD=DE=EA, BCE=CDA=3AB.
∴∠A=∠B.
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形.
新课讲解
证明(2):五边形ABCDE是☉O的内接正
五边形.连接OA,OB,OC.则
∠OAB=∠OBA=∠OBC=∠OCB,
∵ TP,PQ,QR分别是以点A,B,C
为切点的☉O的切线,
∴∠OAP=∠OBP=∠OBQ=∠OCQ,
∴∠PAB=∠PBA=∠QBC=∠QCB.
·
A
O
E
D
C
B
P
Q
R
S
T
新课讲解
又∵AB=BC,
∴ △PAB≌△QBC,
∴ ∠P=∠Q,PQ=2PA.
同理,得
∠Q=∠R=∠S=∠T,
QR=RS=ST=TP=2PA.
∵五边形PQRST的各边与☉O相切,
∴五边形PQRST是☉O的外切正五边形.
·
A
O
E
D
C
B
P
Q
R
S
T
新课讲解
结论
把圆分成n(n>2)等份,依次连接过等分点作圆的切线,各切线相交所得的多边形就是这个圆的一个外切正n边形.
把圆分成n(n>2)等份,依次连接各分点所得的多边形就是这个圆的一个内接正n边形.
1. 用量角器等分圆:
新课讲解
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可以等分圆周,从而得到正多边形.采用“先用量角器画一个的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”.这种方法简便,且可以画任意正多边形、误差小.
2. 用尺规等分圆:
用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形,这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法,但在作图时较复杂,同样存在作图的误差.
新课讲解
例
典例分析
2 利用尺规作图,作出已知圆的内接正方形
作法:(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
A
C
O
B
D
新课讲解
练一练
1
作一个正三角形,使其半径为0.9 cm.
作法一:(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°,
与⊙O分别交于点A,B,C;
(3)连接 AB,BC,CA.则△ABC为所求
作的正三角形,如图所示.
新课讲解
练一练
作法二:(1)作半径为0.9 cm的⊙O;
(2)作⊙O的任一直径AB;
(3)分别以A,B为圆心,以0.9 cm
为半径作弧,交⊙O于C,F和D,E;
(4)连接AD,DE,EA.则△ADE为所
求作的正三角形,如图所示.
课堂小结
正多边形与圆
正多边形
正多边形与圆的关系
各边相等
各角相等
缺一不可
内接正多边形
外切正多边形
正多边形的画法
量角器等分圆周
尺规等分圆周
当堂小练
1 下列给出四个命题:
①正多边形都有内切圆和外接圆,且这两个圆是同心圆;
②各边相等的圆外切多边形是正多边形;
③各角相等的圆内接多边形是正多边形;
④正多边形既是轴对称图形又是中心对称图形.
其中正确命题有( )
A.1个 B.2个
C.3个 D.4个
A
当堂小练
2. 如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
C
拓展与延伸
1.用尺规作图(不要求写作法和证明,但要保留作图痕迹).
(1)如图,已知正五边形ABCDE,求作它的中心O.
(2)如图,已知☉O,求作☉O的内接正八边形.
解:(1)如图①,点O即为所求.
(2)如图②,八边形ABCDEFGH即为所求.
第24章 圆
24.6 正多边形与圆
课时1 正多边形与圆
1.理解并掌握正多边形和圆的有关概念,并能进行相关计算.(重难点)
2.学会通过等分圆周的方法作正多边形.
学习目标
新课导入
情境导入
观看下面这些美丽的图案,都是在日常生活中经常能看到的.你能从这些图案中找出类似的图形吗
新课讲解
知识点1 正多边形的概念
正多边形:各边相等,各角也相等的多边形
三条边相等,
三个角也相等(60度)。
四条边都相等,
四个角也相等(90度)。
新课讲解
例
典例分析
1 下列说法不正确的是( )
A.等边三角形是正多边形
B.各边相等,各角相等的多边形是正多边形
C.菱形不一定是正多边形
D.各角相等的多边形是正多边形
解析:等边三角形是正三角形;当菱形的四角相等时
才是正多边 形(正方形),所以菱形不一定是正多边形;
各边相等,各角相等的多边形是正多边形,故D不对.
D
新课讲解
练一练
1
2
下列说法正确的是( )
A.平行四边形是正多边形 B.矩形是正四边形
C.菱形是正四边形 D.正方形是正四边形
⌒
D
45°
如图,正方形ABCD是☉O的内接正
方形,P是劣弧CD上不同于点C的任
意一点,则∠BPC的度数是 .
新课讲解
知识点2 利用圆画正多边形
问题一 如图,把☉O进行5等分,依次连接各等分点得到五边形ABCDE .分别过点A,B,C,D,E作☉O的切线,切线交于点P,Q,R,S,T,依次连接各交点。得到五边形PQRST.
(1)五边形ABCDE是正多边形吗?
(2)五边形PQRST是正多边形吗?
合作探究
新课讲解
证明(1):如图,把⊙O分成相等的5段弧,
依次连接各分点得到五边形ABCDE.
·
A
O
E
D
C
B
⌒
⌒
⌒
⌒
⌒
∵AB=BC=CD=DE=EA,
⌒
⌒
⌒
∴AB=BC=CD=DE=EA, BCE=CDA=3AB.
∴∠A=∠B.
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形.
新课讲解
证明(2):五边形ABCDE是☉O的内接正
五边形.连接OA,OB,OC.则
∠OAB=∠OBA=∠OBC=∠OCB,
∵ TP,PQ,QR分别是以点A,B,C
为切点的☉O的切线,
∴∠OAP=∠OBP=∠OBQ=∠OCQ,
∴∠PAB=∠PBA=∠QBC=∠QCB.
·
A
O
E
D
C
B
P
Q
R
S
T
新课讲解
又∵AB=BC,
∴ △PAB≌△QBC,
∴ ∠P=∠Q,PQ=2PA.
同理,得
∠Q=∠R=∠S=∠T,
QR=RS=ST=TP=2PA.
∵五边形PQRST的各边与☉O相切,
∴五边形PQRST是☉O的外切正五边形.
·
A
O
E
D
C
B
P
Q
R
S
T
新课讲解
结论
把圆分成n(n>2)等份,依次连接过等分点作圆的切线,各切线相交所得的多边形就是这个圆的一个外切正n边形.
把圆分成n(n>2)等份,依次连接各分点所得的多边形就是这个圆的一个内接正n边形.
1. 用量角器等分圆:
新课讲解
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角可以等分圆周,从而得到正多边形.采用“先用量角器画一个的圆心角,然后在圆上依次截取这个圆心角所对弧的等弧”.这种方法简便,且可以画任意正多边形、误差小.
2. 用尺规等分圆:
用尺规作图的方法等分圆周,然后依次连接圆上各分点得到正多边形,这种方法有局限性,不是任意正多边形都能用此法作图,这种方法从理论上讲是一种准确方法,但在作图时较复杂,同样存在作图的误差.
新课讲解
例
典例分析
2 利用尺规作图,作出已知圆的内接正方形
作法:(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
A
C
O
B
D
新课讲解
练一练
1
作一个正三角形,使其半径为0.9 cm.
作法一:(1)作半径为0.9 cm的⊙O;
(2)用量角器画∠AOB =∠BOC =120°,
与⊙O分别交于点A,B,C;
(3)连接 AB,BC,CA.则△ABC为所求
作的正三角形,如图所示.
新课讲解
练一练
作法二:(1)作半径为0.9 cm的⊙O;
(2)作⊙O的任一直径AB;
(3)分别以A,B为圆心,以0.9 cm
为半径作弧,交⊙O于C,F和D,E;
(4)连接AD,DE,EA.则△ADE为所
求作的正三角形,如图所示.
课堂小结
正多边形与圆
正多边形
正多边形与圆的关系
各边相等
各角相等
缺一不可
内接正多边形
外切正多边形
正多边形的画法
量角器等分圆周
尺规等分圆周
当堂小练
1 下列给出四个命题:
①正多边形都有内切圆和外接圆,且这两个圆是同心圆;
②各边相等的圆外切多边形是正多边形;
③各角相等的圆内接多边形是正多边形;
④正多边形既是轴对称图形又是中心对称图形.
其中正确命题有( )
A.1个 B.2个
C.3个 D.4个
A
当堂小练
2. 如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
C
拓展与延伸
1.用尺规作图(不要求写作法和证明,但要保留作图痕迹).
(1)如图,已知正五边形ABCDE,求作它的中心O.
(2)如图,已知☉O,求作☉O的内接正八边形.
解:(1)如图①,点O即为所求.
(2)如图②,八边形ABCDEFGH即为所求.
