24.6.2 正多边形的性质 课件(共18张PPT)
文档属性
| 名称 | 24.6.2 正多边形的性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 359.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
第24章 圆
24.6 正多边形与圆
课时2 正多边形的性质
1.进一步了解正多边形的有关概念.
2.理解并掌握正多边形与圆之间的关系,并能运用其进行相关的计算. (重难点)
学习目标
新课导入
情境导入
如图,要拧开一个边长为6cm的正六边形螺帽,扳手张开的开口至少是多少?你能想办法知道吗?
新课讲解
知识点1 正多边形的性质
合作探究
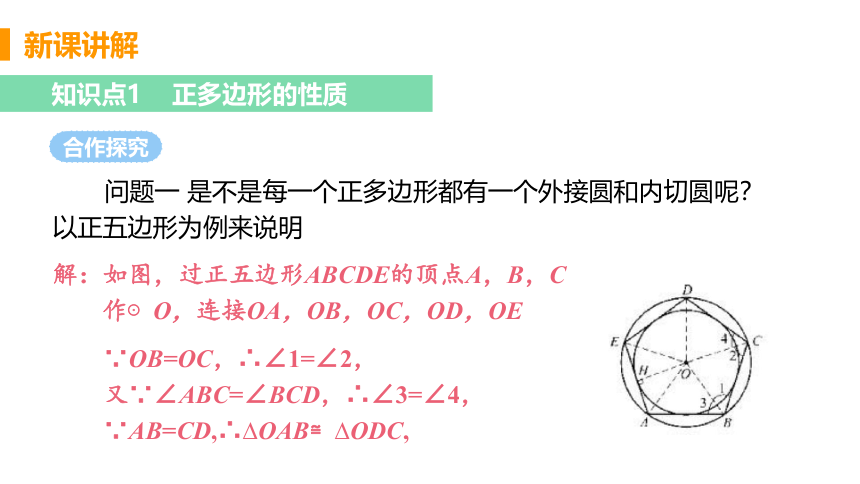
问题一 是不是每一个正多边形都有一个外接圆和内切圆呢?以正五边形为例来说明
解:如图,过正五边形ABCDE的顶点A,B,C
作⊙O,连接OA,OB,OC,OD,OE
∵OB=OC,∴∠1=∠2,
又∵∠ABC=∠BCD,∴∠3=∠4,
∵AB=CD,∴ OAB≌ ODC,
新课讲解
∴OA=OD,
即点D在⊙O,同理点E也在⊙O,
∴正五边形ABCDE有一个以O为圆心的外接圆
正五边形ABCDE的各边是⊙O中相等的弦,等弦的弦心距也相等,所以以点O为圆心OH为半径的圆与正五边形的各边都相切。
任何正多边形都有一个外接圆和一个内切圆,
并且这两个圆是同心圆.
新课讲解
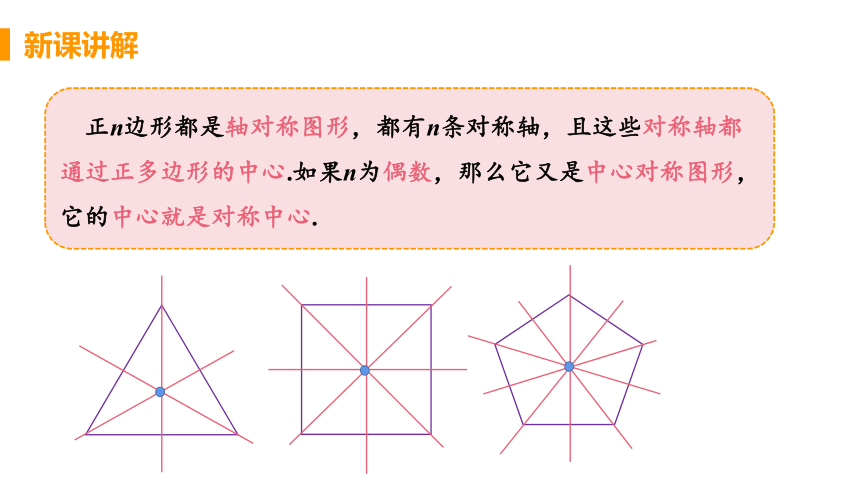
正n边形都是轴对称图形,都有n条对称轴,且这些对称轴都通过正多边形的中心.如果n为偶数,那么它又是中心对称图形,它的中心就是对称中心.
新课讲解
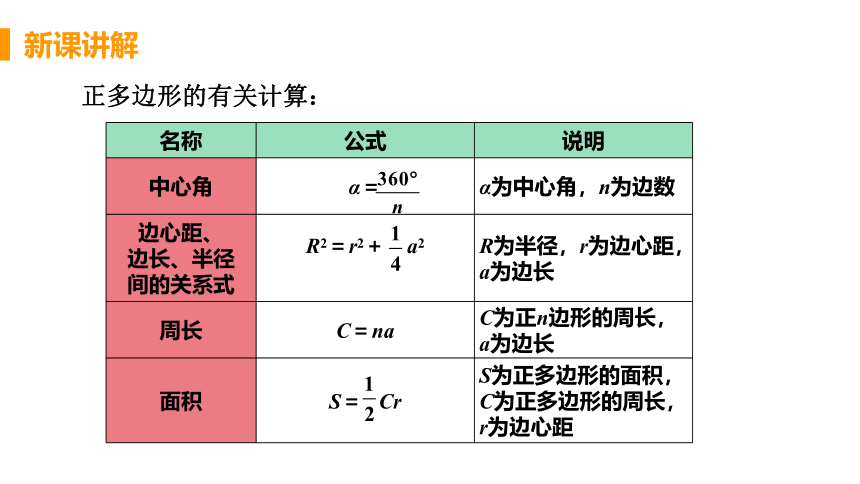
名称 公式 说明
中心角 α= α为中心角,n为边数
边心距、 边长、半径 间的关系式 R2=r2+ a2 R为半径,r为边心距,a为边长
周长 C=na C为正n边形的周长,a为边长
面积 S= Cr S为正多边形的面积,C为正多边形的周长,r为边心距
正多边形的有关计算:
新课讲解
例
典例分析
1 求边长为a的正六边形的周长和面积.
解:如图,过正六边形的中心O作OG⊥BC,垂足为G,连接OB,OC,设该正六边形的周长和面积分别为l和S.
∵ 多边形ABCDEF为正六边形,
∴ ∠BOC=60°,△BOC是等边三角形.
∴ C=6BC=6a.
在△BOC中,有
∴
F
A
B
C
D
E
O
G
新课讲解
例
典例分析
3 一个上、下底面为全等正六边形的礼盒,高为10 cm,上、下底面正六边形的边长为12 cm,如果用彩色胶带按如图所示方式包扎礼盒,所需胶带长度至少为________________.
解:胶带包括上、下面各3段,侧面6段.上、下面中的每段胶
带长等于图中的OC的2倍.利用中心角可求得∠COB=
30°,由正六边形的边长为12 cm,易得BC=6 cm,所以
OB=12 cm,由勾股定理得OC= cm,从
而求得上、下面每段胶带长为 cm,进而求出所需胶
带的长度为 .
新课讲解
新课讲解
练一练
1
2
下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
在正三角形、正方形、正五边形、正六边形中,中心对称
图形有( )
A.0个 B.1个 C.2个 D.4个
A
C
新课讲解
3
4
如图,正五边形ABCDE和正三角形AMN都是☉O的内接多边形,则∠BOM= °.
48
若正多边形的边心距与半径的比为1∶2,则这个正多边形的边数是 .
3
课堂小结
正多边形的性质
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正多边形的对称性
当堂小练
1. 正多边形的一边所对的中心角与该多边形的一个内角
的关系为( )
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
2. 正六边形的边心距与边长之比为( )
A. ∶3 B. ∶2
C.1∶2 D. ∶2
B
B
当堂小练
3. 有一个亭子,它的地基是半径为4 m的正六边形,求地基的
周长和面积 (精确到0.1 m2).
C
D
O
E
F
A
抽象成
B
当堂小练
利用勾股定理,可得边心距
亭子地基的面积:
在Rt△OMB中,OB=4, MB=
解:过点O作OM⊥BC于M.
O
A
B
C
D
E
F
M
r
D
拓展与延伸
1. 如图(1)(2)(3)…,M,N分别是⊙O的内接正三角形ABC、正
方形ABCD、正五边形ABCDE……的边AB,BC上的点,且
BM=CN,连接OM,ON.
(1)求图(1)中∠MON的度数;
(2)图(2)中∠MON的度数是________,图(3)中∠MON
的度数是________;
(3)试探究∠MON的度数与正n边形边数n(n≥3)的关系式
(直接写出答案).
解:(1)如图 (2),连接OB,OC.
易知∠BOC= =120°,∠OBM=∠OCN=30°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN.∴∠BOM=∠CON.
∴∠BON+∠BOM=∠BON+∠CON,
∴∠MON=∠BOC=120°.
(2)90°;72°
(3)∠MON= (n≥3).
拓展与延伸
第24章 圆
24.6 正多边形与圆
课时2 正多边形的性质
1.进一步了解正多边形的有关概念.
2.理解并掌握正多边形与圆之间的关系,并能运用其进行相关的计算. (重难点)
学习目标
新课导入
情境导入
如图,要拧开一个边长为6cm的正六边形螺帽,扳手张开的开口至少是多少?你能想办法知道吗?
新课讲解
知识点1 正多边形的性质
合作探究
问题一 是不是每一个正多边形都有一个外接圆和内切圆呢?以正五边形为例来说明
解:如图,过正五边形ABCDE的顶点A,B,C
作⊙O,连接OA,OB,OC,OD,OE
∵OB=OC,∴∠1=∠2,
又∵∠ABC=∠BCD,∴∠3=∠4,
∵AB=CD,∴ OAB≌ ODC,
新课讲解
∴OA=OD,
即点D在⊙O,同理点E也在⊙O,
∴正五边形ABCDE有一个以O为圆心的外接圆
正五边形ABCDE的各边是⊙O中相等的弦,等弦的弦心距也相等,所以以点O为圆心OH为半径的圆与正五边形的各边都相切。
任何正多边形都有一个外接圆和一个内切圆,
并且这两个圆是同心圆.
新课讲解
正n边形都是轴对称图形,都有n条对称轴,且这些对称轴都通过正多边形的中心.如果n为偶数,那么它又是中心对称图形,它的中心就是对称中心.
新课讲解
名称 公式 说明
中心角 α= α为中心角,n为边数
边心距、 边长、半径 间的关系式 R2=r2+ a2 R为半径,r为边心距,a为边长
周长 C=na C为正n边形的周长,a为边长
面积 S= Cr S为正多边形的面积,C为正多边形的周长,r为边心距
正多边形的有关计算:
新课讲解
例
典例分析
1 求边长为a的正六边形的周长和面积.
解:如图,过正六边形的中心O作OG⊥BC,垂足为G,连接OB,OC,设该正六边形的周长和面积分别为l和S.
∵ 多边形ABCDEF为正六边形,
∴ ∠BOC=60°,△BOC是等边三角形.
∴ C=6BC=6a.
在△BOC中,有
∴
F
A
B
C
D
E
O
G
新课讲解
例
典例分析
3 一个上、下底面为全等正六边形的礼盒,高为10 cm,上、下底面正六边形的边长为12 cm,如果用彩色胶带按如图所示方式包扎礼盒,所需胶带长度至少为________________.
解:胶带包括上、下面各3段,侧面6段.上、下面中的每段胶
带长等于图中的OC的2倍.利用中心角可求得∠COB=
30°,由正六边形的边长为12 cm,易得BC=6 cm,所以
OB=12 cm,由勾股定理得OC= cm,从
而求得上、下面每段胶带长为 cm,进而求出所需胶
带的长度为 .
新课讲解
新课讲解
练一练
1
2
下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
在正三角形、正方形、正五边形、正六边形中,中心对称
图形有( )
A.0个 B.1个 C.2个 D.4个
A
C
新课讲解
3
4
如图,正五边形ABCDE和正三角形AMN都是☉O的内接多边形,则∠BOM= °.
48
若正多边形的边心距与半径的比为1∶2,则这个正多边形的边数是 .
3
课堂小结
正多边形的性质
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正多边形的对称性
当堂小练
1. 正多边形的一边所对的中心角与该多边形的一个内角
的关系为( )
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
2. 正六边形的边心距与边长之比为( )
A. ∶3 B. ∶2
C.1∶2 D. ∶2
B
B
当堂小练
3. 有一个亭子,它的地基是半径为4 m的正六边形,求地基的
周长和面积 (精确到0.1 m2).
C
D
O
E
F
A
抽象成
B
当堂小练
利用勾股定理,可得边心距
亭子地基的面积:
在Rt△OMB中,OB=4, MB=
解:过点O作OM⊥BC于M.
O
A
B
C
D
E
F
M
r
D
拓展与延伸
1. 如图(1)(2)(3)…,M,N分别是⊙O的内接正三角形ABC、正
方形ABCD、正五边形ABCDE……的边AB,BC上的点,且
BM=CN,连接OM,ON.
(1)求图(1)中∠MON的度数;
(2)图(2)中∠MON的度数是________,图(3)中∠MON
的度数是________;
(3)试探究∠MON的度数与正n边形边数n(n≥3)的关系式
(直接写出答案).
解:(1)如图 (2),连接OB,OC.
易知∠BOC= =120°,∠OBM=∠OCN=30°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN.∴∠BOM=∠CON.
∴∠BON+∠BOM=∠BON+∠CON,
∴∠MON=∠BOC=120°.
(2)90°;72°
(3)∠MON= (n≥3).
拓展与延伸
