24.8 综合实践 进球线路与最佳射门角 课件(共16张PPT)
文档属性
| 名称 | 24.8 综合实践 进球线路与最佳射门角 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 11:50:42 | ||
图片预览





文档简介
(共16张PPT)
第24章 圆
24.8 综合实践 进球线路与最佳射门角
课时1 综合实践 进球线路与最佳射门角
1.理解射门点与射门角的概念,并掌握不同情境下的最佳射门点.(重点)
2.如何利用圆的知识进行探究,解决实际问题. (难点)
学习目标
新课导入
情境导入
(1)从图片中,你能获得哪些信息?
(2)你对足球运动有哪些了解?
新课讲解
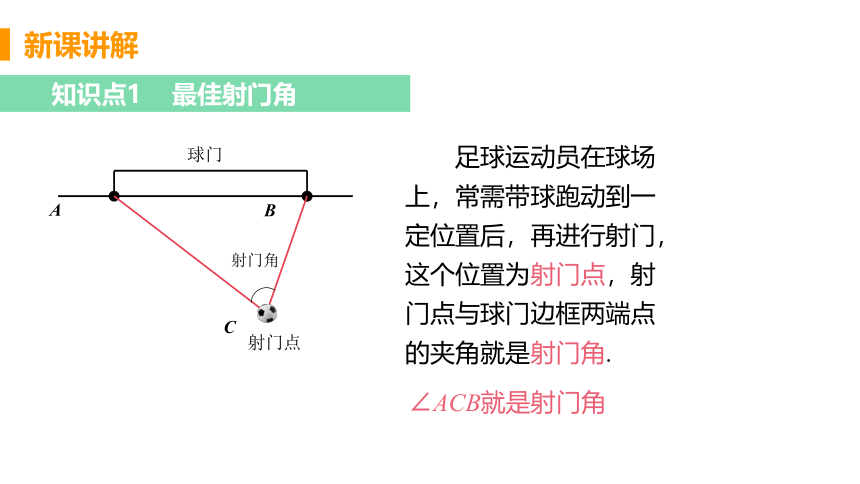
知识点1 最佳射门角
A
B
C
球门
射门点
射门角
足球运动员在球场上,常需带球跑动到一定位置后,再进行射门,这个位置为射门点,射门点与球门边框两端点的夹角就是射门角.
∠ACB就是射门角
在不考虑其他因素的情况下:一般地,射门角越大,射门进球的可能性就越大。
新课讲解
新课讲解
当运动员沿直线 l 横向跑动时,他的位置离球门的中心越近,射门角越大,离球门的中心最近(点C0)时,射门角最大,我们把点C0称为直线 l 上的最佳射门点,∠AC0B 称为直线 l 上的最佳射门角.
最佳射门角的大小与直线 l 到 AB 的距离有关,当直线 l 与 AB 的距离越近,最佳射门角就越大,射门进球的可能性也就越大.
A
B
C
球门
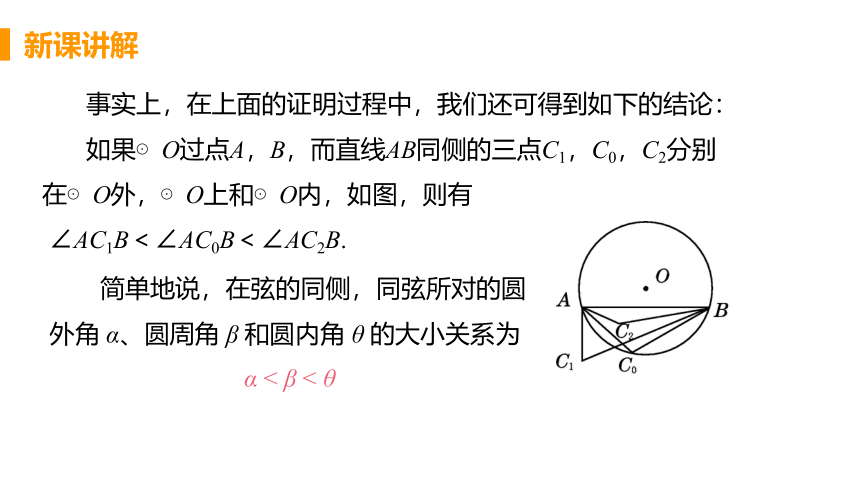
事实上,在上面的证明过程中,我们还可得到如下的结论:
如果⊙O过点A,B,而直线AB同侧的三点C1,C0,C2分别在⊙O外,⊙O上和⊙O内,如图,则有
∠AC1B<∠AC0B<∠AC2B.
简单地说,在弦的同侧,同弦所对的圆外角 α、圆周角 β 和圆内角 θ 的大小关系为
α < β < θ
新课讲解
新课讲解
例
典例分析
1 如在足球比赛场上,甲、乙、丙三名队员互相配合向对方球门MN 进攻,当甲带球冲到A 处时,乙、丙已跟随冲到B,D 处(如图所示),此时甲自己直接射门好,还是迅速将球回传给乙或丙射门好?若选择回传,则选回传给谁更合理?
新课讲解
考虑过M,N 两点以及A,B 中的任意一点作圆,这里
不妨过点M,N,B三点作圆,点A在该圆外,点D在
圆内.设MA交圆于点C,则∠ MAN< ∠ MCN,而∠
MCN= ∠ MBN,所以∠ MAN< ∠ MBN.连接MD,
ND,延长ND 交⊙ O 于点E,连接ME.因为∠ E= ∠ B,
∠ MDN> ∠ E,所以∠ MDN> ∠ B.所以甲应选择回
传,回传给丙更合理.
解:
新课讲解
例
2 足球训练场上,教练在球门前画了一个圆圈进行无 人防守的射门训练.如图,甲、乙两名运动员分别在C,D两处,他们争论不休,都说自己所在的位置对球门AB的张角大,如果你是教练,请评一评他们两个人谁的位置对球门AB的张角大?为什么?
甲、乙两个人所在的位置对球门
AB的张角一样大.根据圆周角定
理的推论可得∠ADB=∠ACB.
解:
新课讲解
练一练
1
2
如图,点A,B,C表示足球比赛中三个不同的射门位置,估测图中各角的大小关系,请指出在图中____点处射门最好.
B
某处靠近海岸的海域有一片暗礁,当地海洋管理部在海岸上建造了两座灯塔A,B,通告所有船只不要进入以AB为弦的弓形区域(阴影部分)内(含边界)以免触礁,如图所示.现有一艘货轮P正向暗礁区域靠近,当∠APB多大时,才能避开暗礁?
解:货轮P在航行时,只要∠APB<55°,即
在ACB外行驶,就能避开暗礁.
课堂小结
1.在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的
圆周角所对的弦也相等.
2.如果⊙O过点A,B,而直线AB同 侧的三点C1,C0,
C2分别在⊙O外,⊙O上和⊙O内,如图,则有
∠AC1B<∠AC0B<∠AC2B.
当堂小练
1. 如图,点P在圆外,点M,N都在圆上,则下列角度大小关系正确的是( )
A.∠APB>∠AMB
B.∠APB>∠ANB
C.∠APB<∠AMB
D.∠ANB>∠AMB
A
B
M
P
N
C
当堂小练
2. 如图,在足球比赛中,甲带球向对方球门AB进攻,当他带球冲到C点时,同伴乙、丙已经分别助攻到点D、E,不考虑防守情况,仅从射门角度考虑,下列说法能够使进球有最佳射门角度的是( )
A.立刻射门
B.带球到点F射门
C.传给同伴乙
D.传给同伴丙
A
B
D
C
E
F
C
D
拓展与延伸
1.如果在线段的同侧有两点向这条线段的两端点所张的 角相等,那么这两点和线段的两端点共圆.即:已知点C,D在线段AB的同侧,且∠ADB=∠ACB,
求证: A,B,C,D四点共圆.
解:假设点D不在A, B, C三点所确定的圆O上 那么点D一定在
圆O内或在圆O外, 若点D在圆O内,则∠ADB>∠ACB
(同圆中,圆内角大于同弧所对的圆周角) 这与已知=
∠ACB矛盾, 若点D在圆O外,则∠ADB<∠ACB
拓展与延伸
(同圆中,圆外角小于同弧所对的圆周角)
这也与已知 ∠ADB=∠ACB矛盾,
所以 点D在圆O内和在圆O外都不可能,
所以 点D必在圆O上,
因为 圆O是A,B,C三点所确定的圆,
所以 A, B, C, D四点共圆。
第24章 圆
24.8 综合实践 进球线路与最佳射门角
课时1 综合实践 进球线路与最佳射门角
1.理解射门点与射门角的概念,并掌握不同情境下的最佳射门点.(重点)
2.如何利用圆的知识进行探究,解决实际问题. (难点)
学习目标
新课导入
情境导入
(1)从图片中,你能获得哪些信息?
(2)你对足球运动有哪些了解?
新课讲解
知识点1 最佳射门角
A
B
C
球门
射门点
射门角
足球运动员在球场上,常需带球跑动到一定位置后,再进行射门,这个位置为射门点,射门点与球门边框两端点的夹角就是射门角.
∠ACB就是射门角
在不考虑其他因素的情况下:一般地,射门角越大,射门进球的可能性就越大。
新课讲解
新课讲解
当运动员沿直线 l 横向跑动时,他的位置离球门的中心越近,射门角越大,离球门的中心最近(点C0)时,射门角最大,我们把点C0称为直线 l 上的最佳射门点,∠AC0B 称为直线 l 上的最佳射门角.
最佳射门角的大小与直线 l 到 AB 的距离有关,当直线 l 与 AB 的距离越近,最佳射门角就越大,射门进球的可能性也就越大.
A
B
C
球门
事实上,在上面的证明过程中,我们还可得到如下的结论:
如果⊙O过点A,B,而直线AB同侧的三点C1,C0,C2分别在⊙O外,⊙O上和⊙O内,如图,则有
∠AC1B<∠AC0B<∠AC2B.
简单地说,在弦的同侧,同弦所对的圆外角 α、圆周角 β 和圆内角 θ 的大小关系为
α < β < θ
新课讲解
新课讲解
例
典例分析
1 如在足球比赛场上,甲、乙、丙三名队员互相配合向对方球门MN 进攻,当甲带球冲到A 处时,乙、丙已跟随冲到B,D 处(如图所示),此时甲自己直接射门好,还是迅速将球回传给乙或丙射门好?若选择回传,则选回传给谁更合理?
新课讲解
考虑过M,N 两点以及A,B 中的任意一点作圆,这里
不妨过点M,N,B三点作圆,点A在该圆外,点D在
圆内.设MA交圆于点C,则∠ MAN< ∠ MCN,而∠
MCN= ∠ MBN,所以∠ MAN< ∠ MBN.连接MD,
ND,延长ND 交⊙ O 于点E,连接ME.因为∠ E= ∠ B,
∠ MDN> ∠ E,所以∠ MDN> ∠ B.所以甲应选择回
传,回传给丙更合理.
解:
新课讲解
例
2 足球训练场上,教练在球门前画了一个圆圈进行无 人防守的射门训练.如图,甲、乙两名运动员分别在C,D两处,他们争论不休,都说自己所在的位置对球门AB的张角大,如果你是教练,请评一评他们两个人谁的位置对球门AB的张角大?为什么?
甲、乙两个人所在的位置对球门
AB的张角一样大.根据圆周角定
理的推论可得∠ADB=∠ACB.
解:
新课讲解
练一练
1
2
如图,点A,B,C表示足球比赛中三个不同的射门位置,估测图中各角的大小关系,请指出在图中____点处射门最好.
B
某处靠近海岸的海域有一片暗礁,当地海洋管理部在海岸上建造了两座灯塔A,B,通告所有船只不要进入以AB为弦的弓形区域(阴影部分)内(含边界)以免触礁,如图所示.现有一艘货轮P正向暗礁区域靠近,当∠APB多大时,才能避开暗礁?
解:货轮P在航行时,只要∠APB<55°,即
在ACB外行驶,就能避开暗礁.
课堂小结
1.在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的
圆周角所对的弦也相等.
2.如果⊙O过点A,B,而直线AB同 侧的三点C1,C0,
C2分别在⊙O外,⊙O上和⊙O内,如图,则有
∠AC1B<∠AC0B<∠AC2B.
当堂小练
1. 如图,点P在圆外,点M,N都在圆上,则下列角度大小关系正确的是( )
A.∠APB>∠AMB
B.∠APB>∠ANB
C.∠APB<∠AMB
D.∠ANB>∠AMB
A
B
M
P
N
C
当堂小练
2. 如图,在足球比赛中,甲带球向对方球门AB进攻,当他带球冲到C点时,同伴乙、丙已经分别助攻到点D、E,不考虑防守情况,仅从射门角度考虑,下列说法能够使进球有最佳射门角度的是( )
A.立刻射门
B.带球到点F射门
C.传给同伴乙
D.传给同伴丙
A
B
D
C
E
F
C
D
拓展与延伸
1.如果在线段的同侧有两点向这条线段的两端点所张的 角相等,那么这两点和线段的两端点共圆.即:已知点C,D在线段AB的同侧,且∠ADB=∠ACB,
求证: A,B,C,D四点共圆.
解:假设点D不在A, B, C三点所确定的圆O上 那么点D一定在
圆O内或在圆O外, 若点D在圆O内,则∠ADB>∠ACB
(同圆中,圆内角大于同弧所对的圆周角) 这与已知=
∠ACB矛盾, 若点D在圆O外,则∠ADB<∠ACB
拓展与延伸
(同圆中,圆外角小于同弧所对的圆周角)
这也与已知 ∠ADB=∠ACB矛盾,
所以 点D在圆O内和在圆O外都不可能,
所以 点D必在圆O上,
因为 圆O是A,B,C三点所确定的圆,
所以 A, B, C, D四点共圆。
