双曲线 河南省上蔡县一高 田鲜丽
图片预览





文档简介
(共13张PPT)
高中数学优质课参赛课题
题目:双曲线及其标准方程
学校:上蔡第一高级中学
姓名: 田鲜丽
个人简历:
田鲜丽 女 1996年毕业于 河南师范大学数学与信息学院数学与应用数学专业, 现在任”省示范高中” 上蔡县第一高级中学数学教师,
参加过”中学教师研究生课程班”学习,多次获高考”先进工作者”, 县级”优秀教师”,河南省数学联赛”优秀辅导员”等荣誉.曾获市教育系统优质课二等奖,撰写的《新课程理念下学生数学思维能力的培养》获驻马店地区高中数学论文一等奖.
授课人:田鲜丽
问题2、把椭圆定义中的“距离的和”改为“距离之差”
那么点的轨迹会怎样?它的方程是怎样的呢?
演示:
【情景设置】
问题1、椭圆的定义是什么?
平面内与两个定点F1、F2的距离和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
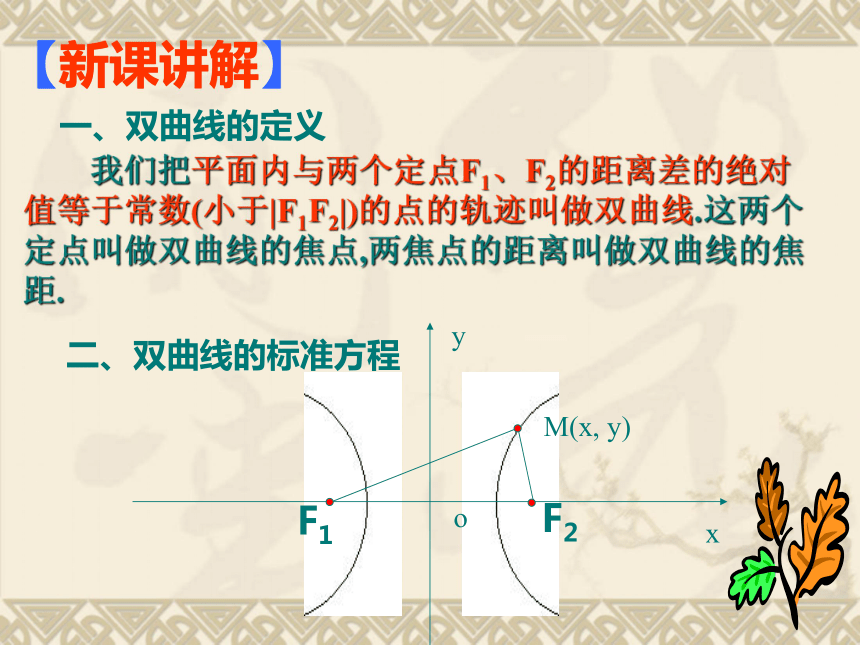
【新课讲解】
我们把平面内与两个定点F1、F2的距离差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距.
一、双曲线的定义
二、双曲线的标准方程
F1
F2
y
x
o
M(x, y)
①建立直角坐标系xoy,使x轴经过点F1、F2,并且原点O与线段F1、F2的中点重合
设M(x, y)是双曲线上任意一点,双曲线的焦距为2c(c>0),那么焦点F1、F2的坐标分别是(-c,0),(c,0).又设点M与F1、F2的距离差的绝对值为2a(a>0),
②由定义知,点M(x, y)属于
集合P={M|||MF1|-|MF2||=2a}
③建立方程:
= ±2a
-
④化简并整理得 :
(c2-a2)x2-a2y2=a2(c2-a2)
由双曲线的定义知,2c>2a,即c>a,所以c2-a2>0.令c2-a2=b2,其中b>0,代入上式,得:
b2x2-a2y2=a2b2
两边同除以a2b2,得
=1 (a>0, b>0)
-
这个方程叫做双曲线的标准方程.它表示的双曲线焦点在x轴上,焦点是F1(-c,0),F2(c,0),这里,a2=c2-b2.
注意:
①如果x2 的系数是正的,那么焦点在x轴上,如果y2 的系数是正的,那么焦点在y轴上,有别于椭圆通过比较分母的大小来判定焦点的位置.
②方程中a,b的含义,与椭圆的标准方程中a,b的含义要区别开.(这里c2-a2=b2).
如果使点F1、F2在y轴上, F1、F2点的坐标分别为1(0, -c),F2(0,c),a, b的意义同上,那么所得方程变为:
=1 (a>0, b>0)
-
这个方程也是双曲线的标准方程.
【典型例题】
已知双曲线的两个焦点的坐标分别是(0,-6),(0,6)且经
过点(2,-5),求双曲线的标准方程
由双曲线的定义知:
【激活练习】
求适合下列条件的双曲线的标准方程:
①a=4,b=3;
答案: ①如果焦点在x轴上方程为
如果焦点在y轴上方程为
-
=1
-
=1
②焦点是(-6 ,0), (6, 0),且经过点(-5, 2).
【小结】
①双曲线的定义;
②双曲线的标准方程;
高中数学优质课参赛课题
题目:双曲线及其标准方程
学校:上蔡第一高级中学
姓名: 田鲜丽
个人简历:
田鲜丽 女 1996年毕业于 河南师范大学数学与信息学院数学与应用数学专业, 现在任”省示范高中” 上蔡县第一高级中学数学教师,
参加过”中学教师研究生课程班”学习,多次获高考”先进工作者”, 县级”优秀教师”,河南省数学联赛”优秀辅导员”等荣誉.曾获市教育系统优质课二等奖,撰写的《新课程理念下学生数学思维能力的培养》获驻马店地区高中数学论文一等奖.
授课人:田鲜丽
问题2、把椭圆定义中的“距离的和”改为“距离之差”
那么点的轨迹会怎样?它的方程是怎样的呢?
演示:
【情景设置】
问题1、椭圆的定义是什么?
平面内与两个定点F1、F2的距离和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
【新课讲解】
我们把平面内与两个定点F1、F2的距离差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距.
一、双曲线的定义
二、双曲线的标准方程
F1
F2
y
x
o
M(x, y)
①建立直角坐标系xoy,使x轴经过点F1、F2,并且原点O与线段F1、F2的中点重合
设M(x, y)是双曲线上任意一点,双曲线的焦距为2c(c>0),那么焦点F1、F2的坐标分别是(-c,0),(c,0).又设点M与F1、F2的距离差的绝对值为2a(a>0),
②由定义知,点M(x, y)属于
集合P={M|||MF1|-|MF2||=2a}
③建立方程:
= ±2a
-
④化简并整理得 :
(c2-a2)x2-a2y2=a2(c2-a2)
由双曲线的定义知,2c>2a,即c>a,所以c2-a2>0.令c2-a2=b2,其中b>0,代入上式,得:
b2x2-a2y2=a2b2
两边同除以a2b2,得
=1 (a>0, b>0)
-
这个方程叫做双曲线的标准方程.它表示的双曲线焦点在x轴上,焦点是F1(-c,0),F2(c,0),这里,a2=c2-b2.
注意:
①如果x2 的系数是正的,那么焦点在x轴上,如果y2 的系数是正的,那么焦点在y轴上,有别于椭圆通过比较分母的大小来判定焦点的位置.
②方程中a,b的含义,与椭圆的标准方程中a,b的含义要区别开.(这里c2-a2=b2).
如果使点F1、F2在y轴上, F1、F2点的坐标分别为1(0, -c),F2(0,c),a, b的意义同上,那么所得方程变为:
=1 (a>0, b>0)
-
这个方程也是双曲线的标准方程.
【典型例题】
已知双曲线的两个焦点的坐标分别是(0,-6),(0,6)且经
过点(2,-5),求双曲线的标准方程
由双曲线的定义知:
【激活练习】
求适合下列条件的双曲线的标准方程:
①a=4,b=3;
答案: ①如果焦点在x轴上方程为
如果焦点在y轴上方程为
-
=1
-
=1
②焦点是(-6 ,0), (6, 0),且经过点(-5, 2).
【小结】
①双曲线的定义;
②双曲线的标准方程;
