-2021-2022学年高一上学期数学 人教A版(2019)必修第一册3.2.1 函数的单调性 课件(共38张PPT)
文档属性
| 名称 | -2021-2022学年高一上学期数学 人教A版(2019)必修第一册3.2.1 函数的单调性 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 345.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 16:40:44 | ||
图片预览





文档简介
(共38张PPT)
3.2函数的基本性质
3.2.1 单调性
前面学习了函数的定义和表示法,
知道函数描述了客观世界中变量之
间的一种对应关系.这样我们就可以
通过研究函数的变化规律来把握客
观世界中事物的变化规律.
新课引入
因此,研究函数的性质,如随着
自变量的增大函数值是增大还是减小,
有没有最高点或最低点,函数图象有
什么特征等,是认识客观规律的重要
方法
请大家回顾初中学习过的一次
函数、二次函数、反比例函数,我
们通过什么来研究它们的性质呢?
图象
2
4
6
-2
-4
-6
x
2
-2
1
-1
x
y
x
y
2
5
-2
-5
y
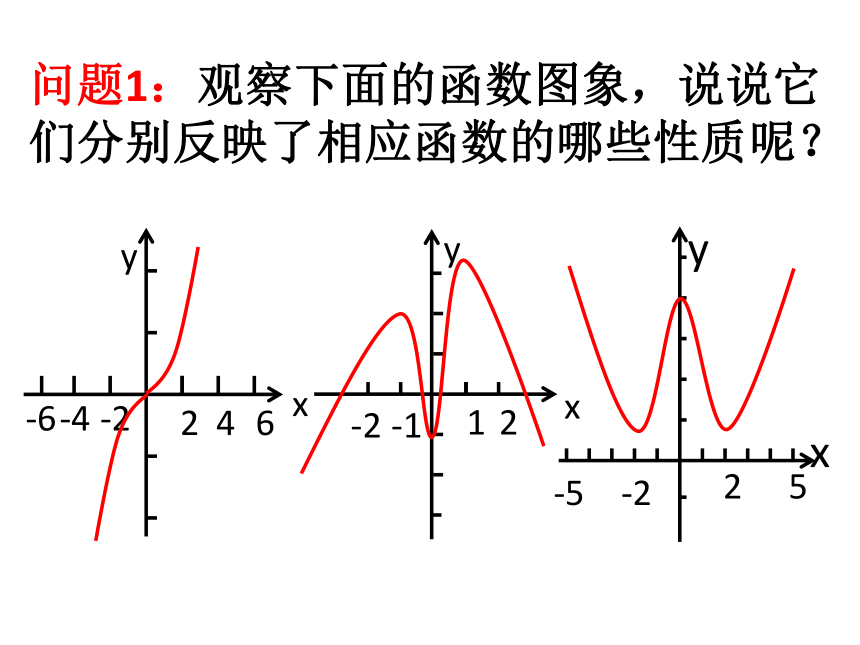
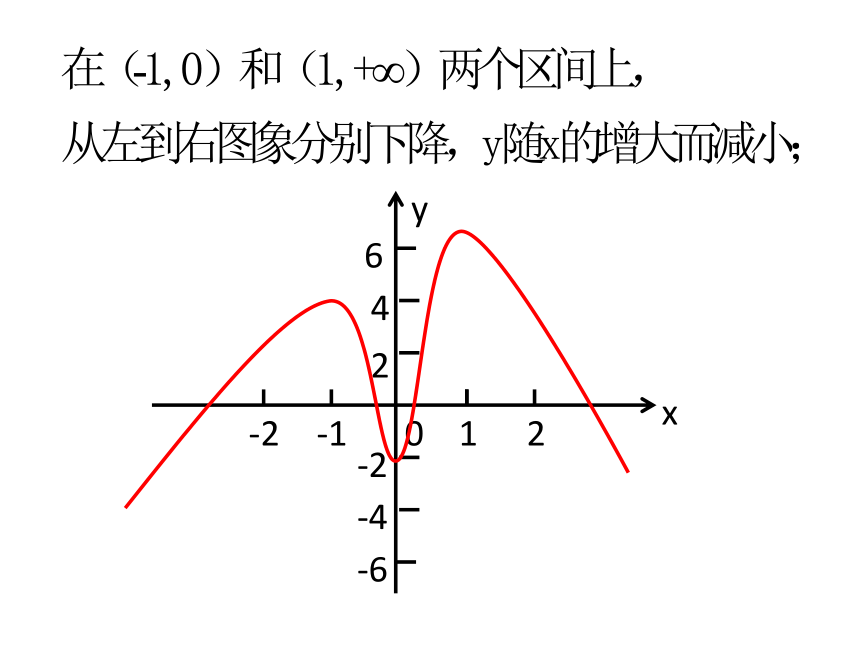
问题1:观察下面的函数图象,说说它
们分别反映了相应函数的哪些性质呢?
2
4
6
-2
-4
-6
x
2
-2
1
-1
x
y
x
y
2
5
-2
-5
y
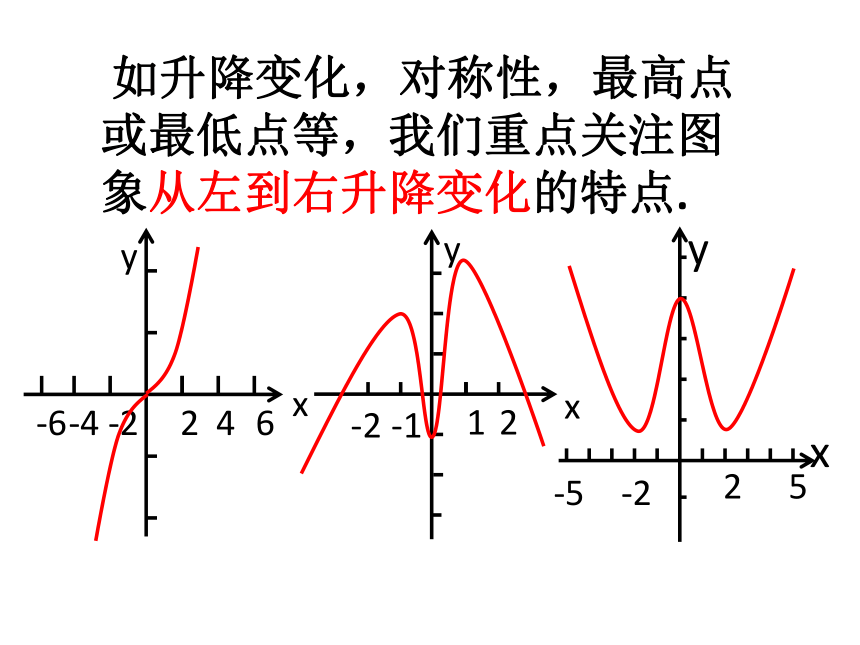
如升降变化,对称性,最高点
或最低点等,我们重点关注图
象从左到右升降变化的特点.
y
2
4
6
-2
-4
-6
50
100
-50
-100
0
x
2
4
6
-2
-4
-6
0
2
-2
1
-1
x
y
2
4
6
-2
-4
-6
0
2
-2
1
-1
x
y
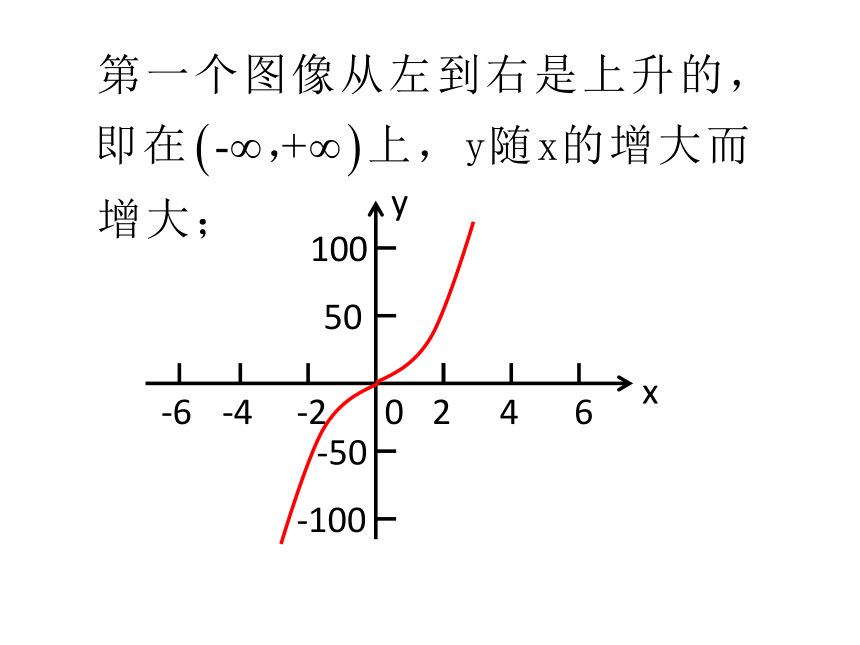
本节课我们从数量上刻画
函数值随自变量的增大而增大
(或减小)的变化规律----函数
的单调性.
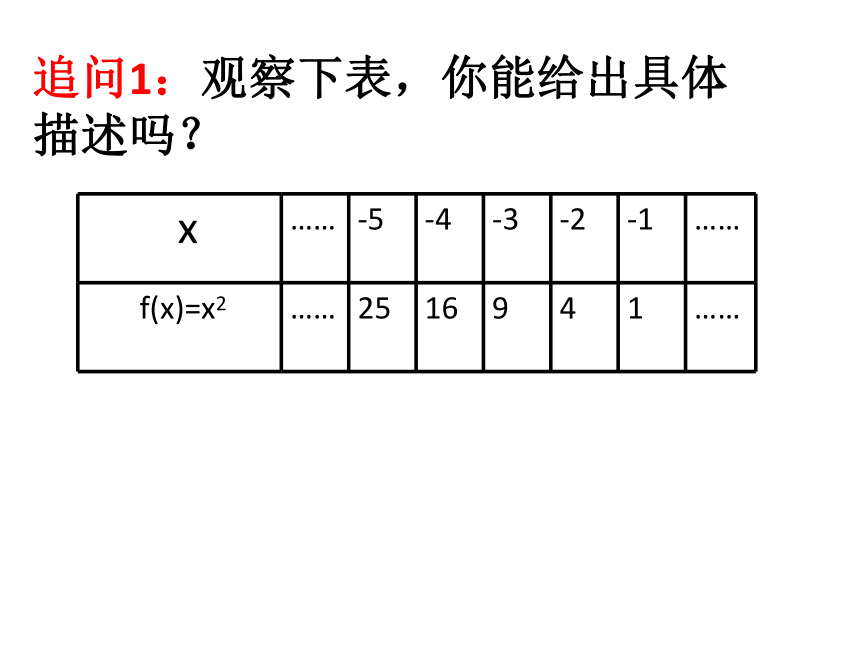
追问1:观察下表,你能给出具体
描述吗?
x …… -5 -4 -3 -2 -1 ……
f(x)=x2 …… 25 16 9 4 1 ……
当x从-5增大到-4,函数值f(x)从25减小到16;
追问2:这样的变化过程能写的完吗?
你能借助字母符号,归纳这些数值变
化的共同点吗?
当x从-4增大到-3,函数值f(x)从16减小到9;
当x从-3增大到-2,函数值f(x)从9减小到4;
y
x
o
a
b
f(a)
f(b)
y=f(x)
追问3:
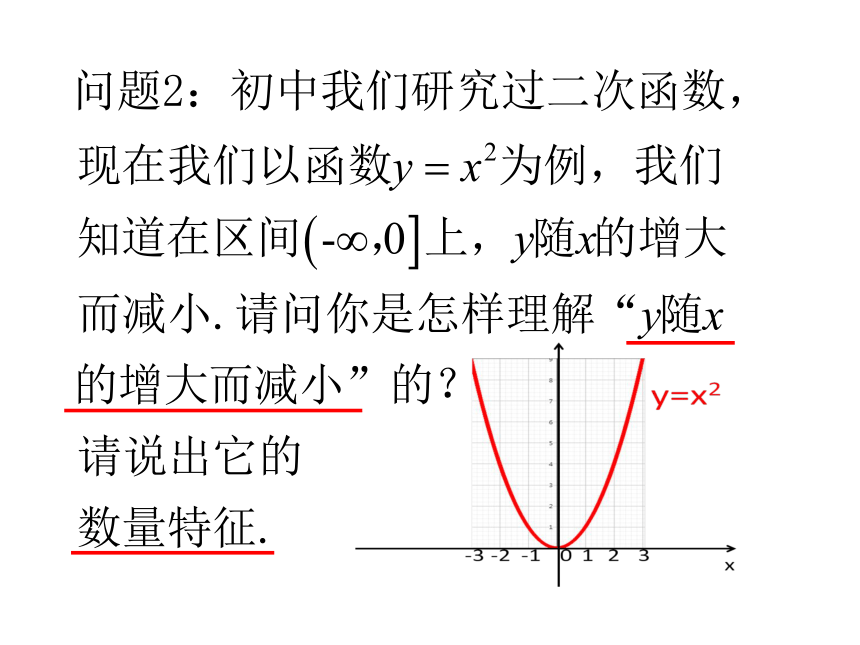
问题3:你能归纳函数y=x2
单调性的刻画方法,给出函数
y=f(x)在区间D上单调性的符号
表述吗?
o
x
y
x1
x2
f(x1)
f(x2)
y=f(x)
o
x
y
x1
x2
f(x1)
f(x2)
y=f(x)
二.函数的单调区间
如果函数y=f(x)在区间D上单调递增
或单调递减,那么就说函数y=f(x)在
这一区间具有(严格的)单调性,
区间D叫做y=f(x)的单调区间.
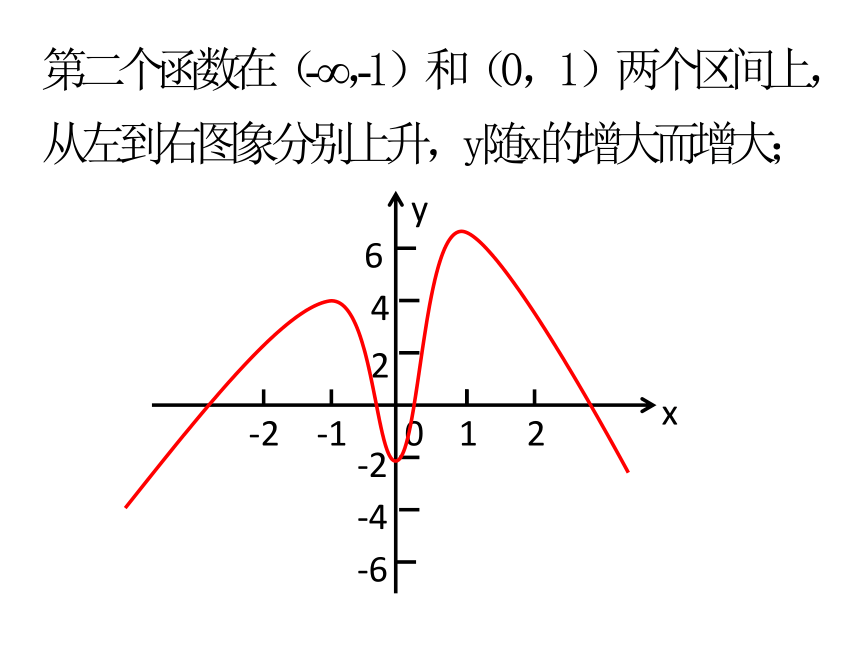
问题4:你能举出在整个定义域内
单调递增的函数(即增函数)例子
吗?你能举出在定义域内的某些区
间上单调递增但在另一些区间
上单调递减的函数例子吗?
1
2
-1
-2
0
2
-2
1
-1
x
y
y=x+1
y=x2
x
y
0
-2
1
-1
2
3
-3
单调性是对定义域内某个区间而
言的,是函数的“局部”性质.描述
函数单调性,要说哪个函数、在哪
个区间上、单调性怎样.
允许函数在某些区间上单调递
增,在另一些区间上单调递减,只
有在整个定义域上单调递增(减)才
能叫增(减)函数.
分析: (1)研究一个函数的单调性,需要利用
单调性的定义,考察在定义域内的哪
些区间上单调递增,在哪些区间上单
调递减;
分析:
(2)具体的操作方法是,在条件x1考察f(x1)与f(x2)的大小关系,比大小可
以作差,这里往往要用到不等式的性质
和代数变形.
在初中,我们利用函数图象得到了
上述结论,这里用严格的推理运算得
到了函数f(x)=kx+b的单调性.
这里将“比较f(x1)与f(x2)的大小”转
化为“比较f(x1)-f(x2)与0的大小”的
做法,体现了数学中“化繁为简”
“化难为易”的转化与化归思想.
由例1的证明过程,归纳
一下用单调性的定义证明一
个函数在区间D上的单调性
的基本步骤.
第一步
第二步
第二步:计算f(x1)-f(x2),将f(x1)-f(x2)
分解为若干个可以直接确定符号
的式子;
第三步
课堂小结
1.(1)单调递增.
(2)单调递减.
(3)单调区间.
(4)证明或研究函数单调性
的基本步骤.
作业
教科书79页练习1,2,3
3.2函数的基本性质
3.2.1 单调性
前面学习了函数的定义和表示法,
知道函数描述了客观世界中变量之
间的一种对应关系.这样我们就可以
通过研究函数的变化规律来把握客
观世界中事物的变化规律.
新课引入
因此,研究函数的性质,如随着
自变量的增大函数值是增大还是减小,
有没有最高点或最低点,函数图象有
什么特征等,是认识客观规律的重要
方法
请大家回顾初中学习过的一次
函数、二次函数、反比例函数,我
们通过什么来研究它们的性质呢?
图象
2
4
6
-2
-4
-6
x
2
-2
1
-1
x
y
x
y
2
5
-2
-5
y
问题1:观察下面的函数图象,说说它
们分别反映了相应函数的哪些性质呢?
2
4
6
-2
-4
-6
x
2
-2
1
-1
x
y
x
y
2
5
-2
-5
y
如升降变化,对称性,最高点
或最低点等,我们重点关注图
象从左到右升降变化的特点.
y
2
4
6
-2
-4
-6
50
100
-50
-100
0
x
2
4
6
-2
-4
-6
0
2
-2
1
-1
x
y
2
4
6
-2
-4
-6
0
2
-2
1
-1
x
y
本节课我们从数量上刻画
函数值随自变量的增大而增大
(或减小)的变化规律----函数
的单调性.
追问1:观察下表,你能给出具体
描述吗?
x …… -5 -4 -3 -2 -1 ……
f(x)=x2 …… 25 16 9 4 1 ……
当x从-5增大到-4,函数值f(x)从25减小到16;
追问2:这样的变化过程能写的完吗?
你能借助字母符号,归纳这些数值变
化的共同点吗?
当x从-4增大到-3,函数值f(x)从16减小到9;
当x从-3增大到-2,函数值f(x)从9减小到4;
y
x
o
a
b
f(a)
f(b)
y=f(x)
追问3:
问题3:你能归纳函数y=x2
单调性的刻画方法,给出函数
y=f(x)在区间D上单调性的符号
表述吗?
o
x
y
x1
x2
f(x1)
f(x2)
y=f(x)
o
x
y
x1
x2
f(x1)
f(x2)
y=f(x)
二.函数的单调区间
如果函数y=f(x)在区间D上单调递增
或单调递减,那么就说函数y=f(x)在
这一区间具有(严格的)单调性,
区间D叫做y=f(x)的单调区间.
问题4:你能举出在整个定义域内
单调递增的函数(即增函数)例子
吗?你能举出在定义域内的某些区
间上单调递增但在另一些区间
上单调递减的函数例子吗?
1
2
-1
-2
0
2
-2
1
-1
x
y
y=x+1
y=x2
x
y
0
-2
1
-1
2
3
-3
单调性是对定义域内某个区间而
言的,是函数的“局部”性质.描述
函数单调性,要说哪个函数、在哪
个区间上、单调性怎样.
允许函数在某些区间上单调递
增,在另一些区间上单调递减,只
有在整个定义域上单调递增(减)才
能叫增(减)函数.
分析: (1)研究一个函数的单调性,需要利用
单调性的定义,考察在定义域内的哪
些区间上单调递增,在哪些区间上单
调递减;
分析:
(2)具体的操作方法是,在条件x1
以作差,这里往往要用到不等式的性质
和代数变形.
在初中,我们利用函数图象得到了
上述结论,这里用严格的推理运算得
到了函数f(x)=kx+b的单调性.
这里将“比较f(x1)与f(x2)的大小”转
化为“比较f(x1)-f(x2)与0的大小”的
做法,体现了数学中“化繁为简”
“化难为易”的转化与化归思想.
由例1的证明过程,归纳
一下用单调性的定义证明一
个函数在区间D上的单调性
的基本步骤.
第一步
第二步
第二步:计算f(x1)-f(x2),将f(x1)-f(x2)
分解为若干个可以直接确定符号
的式子;
第三步
课堂小结
1.(1)单调递增.
(2)单调递减.
(3)单调区间.
(4)证明或研究函数单调性
的基本步骤.
作业
教科书79页练习1,2,3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
