人教版(2019)必修第二册《第6章+圆周运动》2021年单元测试卷(3word版含答案)
文档属性
| 名称 | 人教版(2019)必修第二册《第6章+圆周运动》2021年单元测试卷(3word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 286.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-01 05:45:09 | ||
图片预览


文档简介
人教版(2019)必修第二册《第6章 圆周运动》2021年单元测试卷(3)
一.选择题(共12小题)
1.如图所示,在光滑水平面上,小球在拉力F作用下做匀速圆周运动,拉力F发生变化,则关于小球运动情况的说法正确的是( )
A.若拉力突然变小,小球将沿Pa做离心运动
B.若拉力突然变大,小球将沿Pb做离心运动
C.若拉力突然变小,小球将沿Pc做向心运动
D.若拉力突然消失,小球将沿Pa做匀速直线运动
2.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc C.Fc<Fa<Fb D.Fa>Fc>Fb
3.下列关于离心运动的叙述中不正确的是( )
A.离心运动是由于合力不足以提供向心力而引起的
B.离心运动的轨迹一定是直线
C.洗衣机的脱水筒是利用离心运动把湿衣服甩干的
D.汽车转弯时速度过大,会因离心运动造成交通事故
4.长度为L=0.5m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
A.6.0N的压力 B.6.0N的拉力 C.24N的压力 D.24N的拉力
5.一精确转动的机械手表,秒针的角速度大约为( )
A.0.05rad/s B.0.1rad/s C.1rad/s D.6rad/s
6.暗物质是二十一世纪物理学之谜,对该问题的研究可能带来一场物理学的革命.为了探测暗物质,我国在2015年12月17日成功发射了一颗被命名为“悟空”的暗物质探测卫星.已知“悟空”在低于同步卫星的轨道上绕地球做匀速圆周运动(t小于其运动周期),运动的弧长为s,与地球中心连线扫过的角度为β(弧度),则下列说法中正确的是( )
A.“悟空”的线速度大于第一宇宙速度
B.“悟空”的向心加速度小于地球同步卫星的向心加速度
C.“悟空”的环绕周期为
D.“悟空”的质量为
7.如图所示,两个质量相同的小球A、B,用长度之比为LA:LB=3:2的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的( )
A.角速度之比为ωA:ωB=3:2
B.线速度之比为vA:vB=1:1
C.向心力之比为FA:FB=2:3
D.悬线的拉力之比为TA:TB=3:2
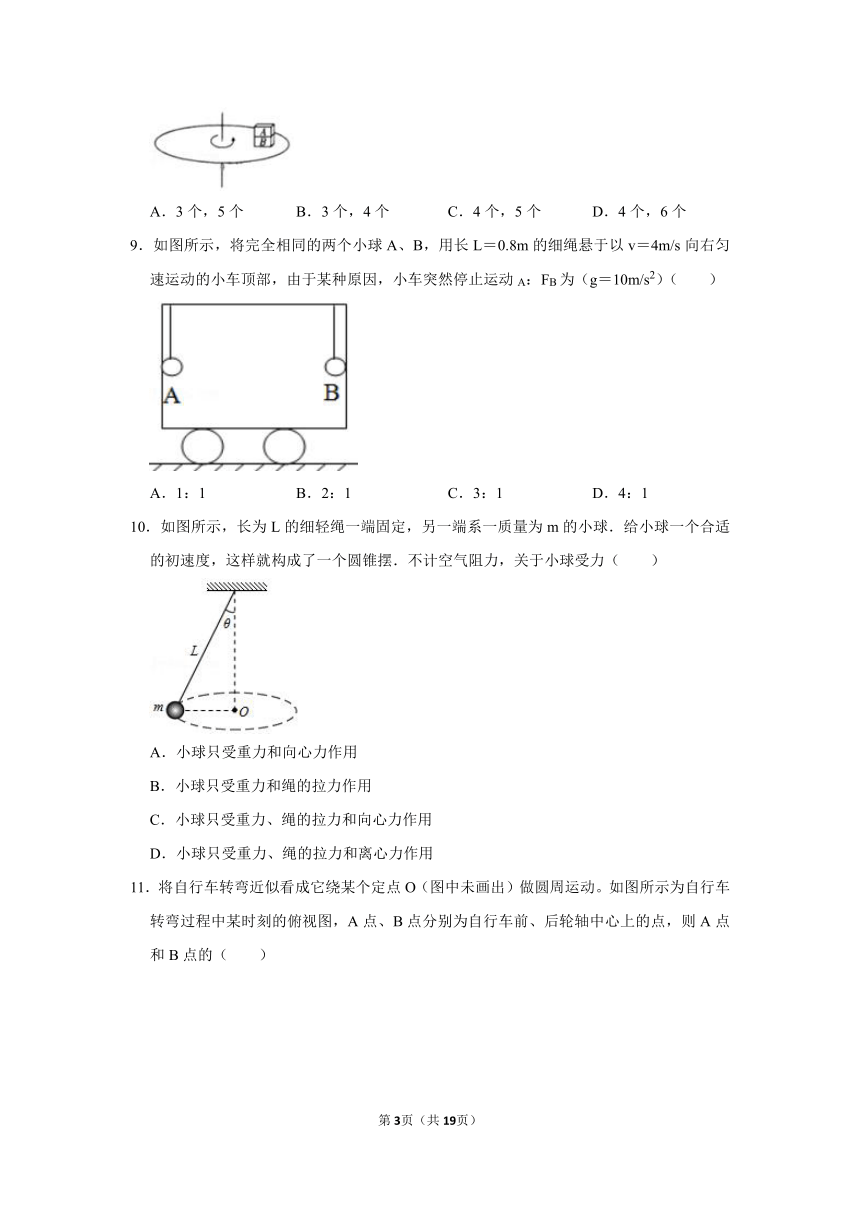
8.如图所示,A、B两个物体与圆盘保持相对静止,随圆盘一起做匀速圆周运动( )
A.3个,5个 B.3个,4个 C.4个,5个 D.4个,6个
9.如图所示,将完全相同的两个小球A、B,用长L=0.8m的细绳悬于以v=4m/s向右匀速运动的小车顶部,由于某种原因,小车突然停止运动A:FB为(g=10m/s2)( )
A.1:1 B.2:1 C.3:1 D.4:1
10.如图所示,长为L的细轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,这样就构成了一个圆锥摆.不计空气阻力,关于小球受力( )
A.小球只受重力和向心力作用
B.小球只受重力和绳的拉力作用
C.小球只受重力、绳的拉力和向心力作用
D.小球只受重力、绳的拉力和离心力作用
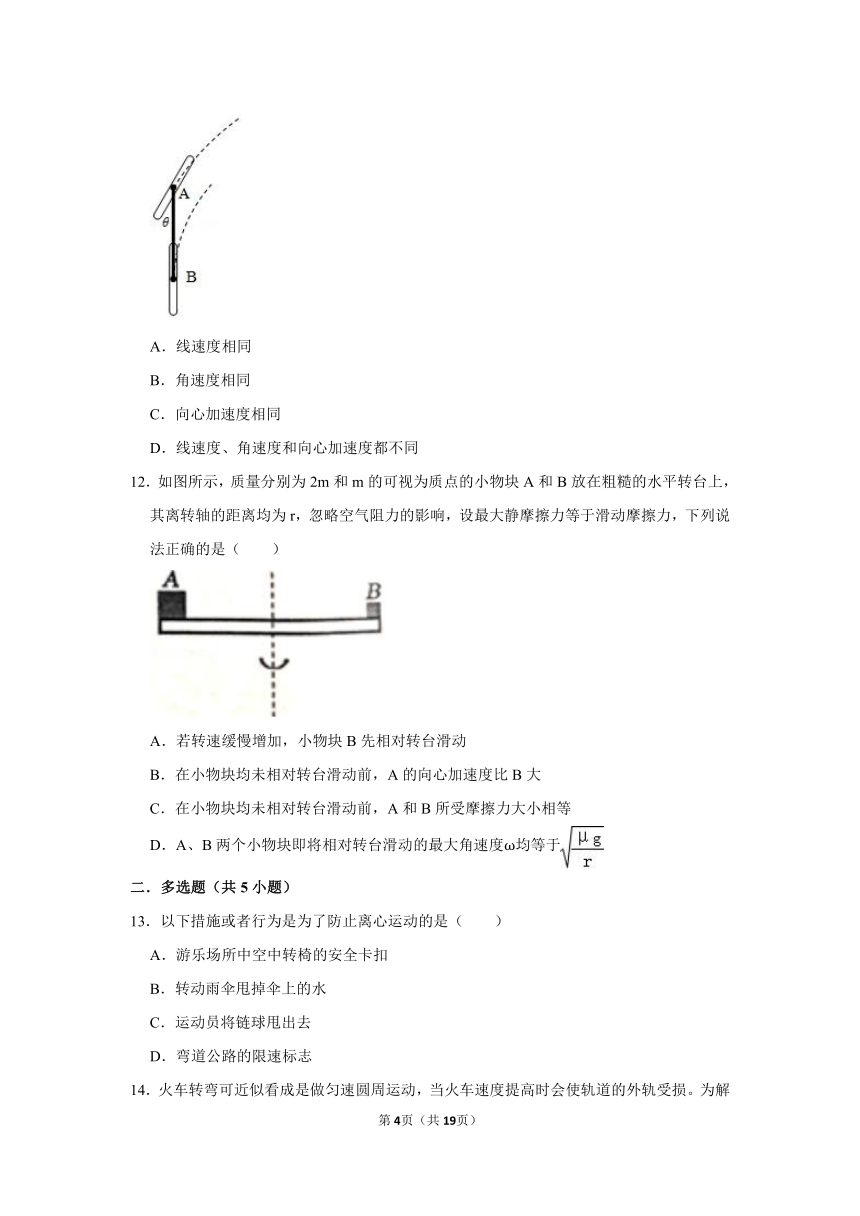
11.将自行车转弯近似看成它绕某个定点O(图中未画出)做圆周运动。如图所示为自行车转弯过程中某时刻的俯视图,A点、B点分别为自行车前、后轮轴中心上的点,则A点和B点的( )
A.线速度相同
B.角速度相同
C.向心加速度相同
D.线速度、角速度和向心加速度都不同
12.如图所示,质量分别为2m和m的可视为质点的小物块A和B放在粗糙的水平转台上,其离转轴的距离均为r,忽略空气阻力的影响,设最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A.若转速缓慢增加,小物块B先相对转台滑动
B.在小物块均未相对转台滑动前,A的向心加速度比B大
C.在小物块均未相对转台滑动前,A和B所受摩擦力大小相等
D.A、B两个小物块即将相对转台滑动的最大角速度ω均等于
二.多选题(共5小题)
13.以下措施或者行为是为了防止离心运动的是( )
A.游乐场所中空中转椅的安全卡扣
B.转动雨伞甩掉伞上的水
C.运动员将链球甩出去
D.弯道公路的限速标志
14.火车转弯可近似看成是做匀速圆周运动,当火车速度提高时会使轨道的外轨受损。为解决火车高速转弯时不使外轨受损这一难题,你认为以下措施可行的是( )
A.适当增高内轨 B.适当增高外轨
C.减小弯道半径 D.增大弯道半径
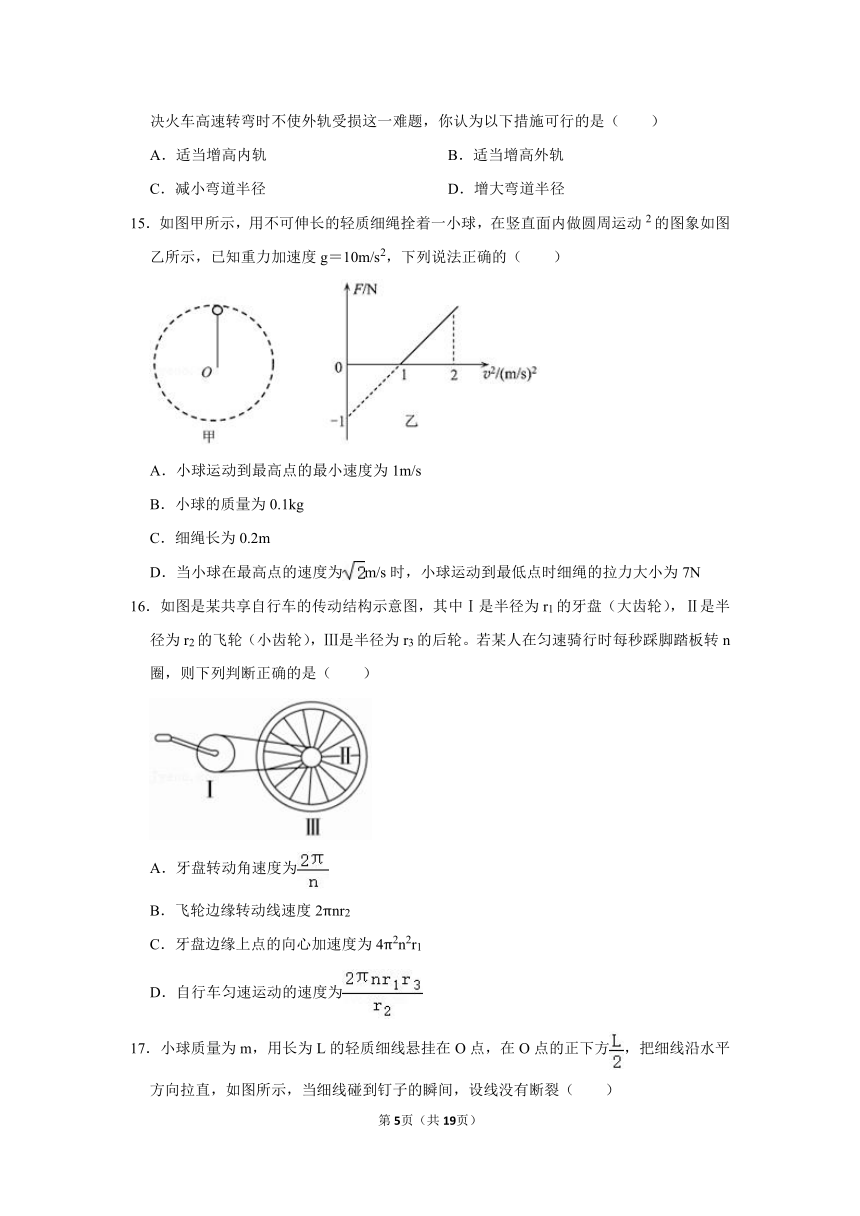
15.如图甲所示,用不可伸长的轻质细绳拴着一小球,在竖直面内做圆周运动2的图象如图乙所示,已知重力加速度g=10m/s2,下列说法正确的( )
A.小球运动到最高点的最小速度为1m/s
B.小球的质量为0.1kg
C.细绳长为0.2m
D.当小球在最高点的速度为m/s时,小球运动到最低点时细绳的拉力大小为7N
16.如图是某共享自行车的传动结构示意图,其中Ⅰ是半径为r1的牙盘(大齿轮),Ⅱ是半径为r2的飞轮(小齿轮),Ⅲ是半径为r3的后轮。若某人在匀速骑行时每秒踩脚踏板转n圈,则下列判断正确的是( )
A.牙盘转动角速度为
B.飞轮边缘转动线速度2πnr2
C.牙盘边缘上点的向心加速度为4π2n2r1
D.自行车匀速运动的速度为
17.小球质量为m,用长为L的轻质细线悬挂在O点,在O点的正下方,把细线沿水平方向拉直,如图所示,当细线碰到钉子的瞬间,设线没有断裂( )
A.小球的角速度突然增大
B.小球的瞬时速度突然增大
C.小球的向心加速度突然增大
D.小球对悬线的拉力保持不变
三.解答题(共2小题)
18.近年,我国的高铁发展非常迅猛.为了保证行车安全,车辆转弯的技术要求是相当高的.如果在转弯处铺成如图所示内、外等高的轨道,火车的 (选填“外轮”、“内轮”)对轨道有侧向挤压,容易导致翻车事故.为此,铺设轨道时应该把 (选填“外轨”、“内轨”)适当降低一定的高度.如果两轨道间距为L,内外轨高度差为h,弯道半径为R .
19.如图,支架质量为M,置于水平地面上.轴O处有一长为L的杆(质量不计),支架保持静止.若小球到达最高点时支架对地面的压力恰好为0,求,小球通过最高点速度的大小?
人教版(2019)必修第二册《第6章 圆周运动》2021年单元测试卷(3)
参考答案与试题解析
一.选择题(共12小题)
1.如图所示,在光滑水平面上,小球在拉力F作用下做匀速圆周运动,拉力F发生变化,则关于小球运动情况的说法正确的是( )
A.若拉力突然变小,小球将沿Pa做离心运动
B.若拉力突然变大,小球将沿Pb做离心运动
C.若拉力突然变小,小球将沿Pc做向心运动
D.若拉力突然消失,小球将沿Pa做匀速直线运动
【分析】本题考查离心现象产生原因以及运动轨迹,当向心力突然消失或变小时,物体会做离心运动,运动轨迹可是直线也可以是曲线,要根据受力情况分析.
【解答】解:在水平面上,细绳的拉力提供m所需的向心力,物体所受合力为零。若拉力减小时,拉力增大时,故D正确。
故选:D。
2.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc C.Fc<Fa<Fb D.Fa>Fc>Fb
【分析】由图象知轨道半径大小关系,根据向心力公式F=m比较向心力的大小。
【解答】解:根据向心力公式F=m知v大小相等,向心力越小a>rb>rc,所以Fa<Fb<Fc,故B正确,ACD错误。
故选:B。
3.下列关于离心运动的叙述中不正确的是( )
A.离心运动是由于合力不足以提供向心力而引起的
B.离心运动的轨迹一定是直线
C.洗衣机的脱水筒是利用离心运动把湿衣服甩干的
D.汽车转弯时速度过大,会因离心运动造成交通事故
【分析】当物体受到的合力的大小不足以提供物体所需要的向心力的大小时,物体就要远离圆心,此时物体做的就是离心运动.
【解答】解:AB、当外界提供的向心力突然消失时,物体就要远离圆心,但轨迹不一定是直线,B错误;
C、水滴依附的附着力是一定的,水滴被甩掉;
D、在水平面拐弯、支持力,重力和支持力平衡,由于最大静摩擦力一定,使静摩擦力小于向心力,容易造成事故。
本题选错误的,
故选:B。
4.长度为L=0.5m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
A.6.0N的压力 B.6.0N的拉力 C.24N的压力 D.24N的拉力
【分析】小球在细杆的作用下,在竖直平面内做圆周运动。对最高点受力分析,找出提供向心力的来源,结合已知量可求出最高点小球速率为2m/s时的细杆受到的力。
【解答】解:小球以O点为圆心在竖直平面内做圆周运动,当在最高点小球与细杆无弹力作用时1,则有:
mg=m
得:v1==m/s
由于v7=m/s>2m/s,小球在O点受力分析,有:
mg﹣F支=m
则有:F支=mg﹣m=30N﹣3
所以细杆受到的压力,大小为7N。
故选:A。
5.一精确转动的机械手表,秒针的角速度大约为( )
A.0.05rad/s B.0.1rad/s C.1rad/s D.6rad/s
【分析】角速度是描述物体转动快慢的物理量,加速度ω==
【解答】解:秒针转动一圈的时间为60s,角速度ω==。
故选:B。
6.暗物质是二十一世纪物理学之谜,对该问题的研究可能带来一场物理学的革命.为了探测暗物质,我国在2015年12月17日成功发射了一颗被命名为“悟空”的暗物质探测卫星.已知“悟空”在低于同步卫星的轨道上绕地球做匀速圆周运动(t小于其运动周期),运动的弧长为s,与地球中心连线扫过的角度为β(弧度),则下列说法中正确的是( )
A.“悟空”的线速度大于第一宇宙速度
B.“悟空”的向心加速度小于地球同步卫星的向心加速度
C.“悟空”的环绕周期为
D.“悟空”的质量为
【分析】已知该太空电站经过时间t(t小于太空电站运行的周期),它运动的弧长为s,它与地球中心连线扫过的角度为β(弧度),根据线速度和角速度定义可求得太空站的线速度和角速度,然后根据v=ωr可求得轨道半径;根据万有引力提供向心力求求得地球的质量.
【解答】解:A、该太空电站经过时间t(t小于太空电站运行的周期),它与地球中心连线扫过的角度为β(弧度),
则太空站运行的线速度为 v=
角速度为:ω=
根据v=ωr得轨道半径为:r==
人类第一台太空电站在地球的同步轨道上绕地球做匀速圆周运动,万有引力提供向心力=m,可知卫星的轨道半径越大,第一宇宙速度是近地卫星的环绕速度,故A错误;
B、由G,则知“悟空”的向心加速度大于地球同步卫星的向心加速度。
C、“悟空”的环绕周期为T==;
D、“悟空”绕地球做匀速圆周运动,即:G2,ω=
联立解得:地球的质量为 M=,不能求出“悟空”的质量;
故选:C。
7.如图所示,两个质量相同的小球A、B,用长度之比为LA:LB=3:2的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的( )
A.角速度之比为ωA:ωB=3:2
B.线速度之比为vA:vB=1:1
C.向心力之比为FA:FB=2:3
D.悬线的拉力之比为TA:TB=3:2
【分析】根据小球重力和拉力的合力提供向心力得出角速度的表达式,得出角速度之比,从而得出线速度之比。根据平行四边形定则求出拉力的表达式,从而得出拉力之比。
【解答】解:A、小球靠重力和拉力的合力提供向心力,mgtanθ=mLsinθ ω2,则ω=,由于两球做圆周运动悬点到圆心的距离相等,故A错误。
B、由A选项知,根据v=rω=Lsinθ ω知,则线速度之比不等于1:4。
C、向心力F=mgtanθ,A、B悬线与竖直方向的夹角的余弦之比为2:3,可知向心力之比不等于6:3。
D、悬线拉力T=、B悬线与竖直方向的夹角的余弦之比为2:8A:TB=3:2,故D正确。
故选:D。
8.如图所示,A、B两个物体与圆盘保持相对静止,随圆盘一起做匀速圆周运动( )
A.3个,5个 B.3个,4个 C.4个,5个 D.4个,6个
【分析】分别对A与B进行受力分析即可,要注意向心力是根据效果命名的力,只能由其它力的合力或者分力来充当,不是真实存在的力,不能说物体受到向心力。
【解答】解:A物体在水平面内做匀速圆周运动,一定受到重力和B对A的支持力作用,有背离圆心的运动趋势,且静摩擦力提供向心力;
B物体也在水平面内做匀速圆周运动,一定受到重力和圆盘的支持力作用;物体在转动过程中,因此受到指向圆心的静摩擦力,两个静摩擦力的合力提供向心力。故A正确
故选:A。
9.如图所示,将完全相同的两个小球A、B,用长L=0.8m的细绳悬于以v=4m/s向右匀速运动的小车顶部,由于某种原因,小车突然停止运动A:FB为(g=10m/s2)( )
A.1:1 B.2:1 C.3:1 D.4:1
【分析】小车原来向右匀速运动,突然停止运动时,A球由于惯性,会向前摆动,将做圆周运动,B球受到小车前壁的作用停止运动,在竖直方向上拉力等于重力,根据牛顿第二定律求出A球绳的拉力,从而求出两悬线的拉力之比。
【解答】解:若A、B的质量为m,则
对A球有:FA﹣mg=m,得FA=mg+m=m(10+。
对B球有:FB=mg=10m。
所以FA:FB=3:1.故C正确,A、B。
故选:C。
10.如图所示,长为L的细轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,这样就构成了一个圆锥摆.不计空气阻力,关于小球受力( )
A.小球只受重力和向心力作用
B.小球只受重力和绳的拉力作用
C.小球只受重力、绳的拉力和向心力作用
D.小球只受重力、绳的拉力和离心力作用
【分析】分析小球的受力,受到重力、绳的拉力,二者的合力提供向心力,向心力是效果力,不是重复受力.
【解答】解:小球做匀速圆周运动,合力不为零,提供向心力;
小球受重力和细线的拉力,共2个力,对惯性系没有离心力的说法;
故ACD错误,B正确;
故选:B。
11.将自行车转弯近似看成它绕某个定点O(图中未画出)做圆周运动。如图所示为自行车转弯过程中某时刻的俯视图,A点、B点分别为自行车前、后轮轴中心上的点,则A点和B点的( )
A.线速度相同
B.角速度相同
C.向心加速度相同
D.线速度、角速度和向心加速度都不同
【分析】首先根据A、B绕着同一个点转动,得到A、B两点具有相同的角速度;然后利用公式v=ωr和a=ω2r判断A点和B点线速度和向心加速度是否相同。
【解答】解:B、因为A,所以具有相同的角速度;
A、由v=ωr可知当角速度相等时,线速度也不同;
C、由a=ω2r可知当角速度相等时,转动的半径不同时,故C错误;
D、由上述分析可知A点和B点的角速度相同,故D错误。
故选:B。
12.如图所示,质量分别为2m和m的可视为质点的小物块A和B放在粗糙的水平转台上,其离转轴的距离均为r,忽略空气阻力的影响,设最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A.若转速缓慢增加,小物块B先相对转台滑动
B.在小物块均未相对转台滑动前,A的向心加速度比B大
C.在小物块均未相对转台滑动前,A和B所受摩擦力大小相等
D.A、B两个小物块即将相对转台滑动的最大角速度ω均等于
【分析】当角速度较小时,A、B均靠静摩擦力提供向心力,角速度增大,达到最大静摩擦力,由向心力公式即可求出临界角速度。
【解答】解:AD、对物块受力分析可知,f=mω2r,当f达到最大静摩擦力时,根据牛顿第二定律得:μmg=mrω2,解得A、B两个小物块即将相对转台滑动的最大角速度ω为:ω=,只与物块的转动半径和动摩擦因数有关,两物块一起相对转台滑动,D正确;
B、在小物块均未相对转台滑动前,可知a=ω6r,故A的向心加速度与B的向心加速度大小相等,故B错误;
C、在小物块均未相对转台滑动前2r,可知A和B所受摩擦力大小与质量成正比,故C错误;
故选:D。
二.多选题(共5小题)
13.以下措施或者行为是为了防止离心运动的是( )
A.游乐场所中空中转椅的安全卡扣
B.转动雨伞甩掉伞上的水
C.运动员将链球甩出去
D.弯道公路的限速标志
【分析】当物体提供的力小于所需的向心力,做离心运动,当物体提供的力大于所需的向心力,做近心运动.
【解答】解:A、空中转椅的安全卡扣是为了防止游人被甩出做离心运动而设计的;
B、转动雨伞时,故B错误;
C、运动员将链球甩出去也是利用了链球的离心运动;
D、弯道公路的限速标志是提醒汽车减速至限速以下的速度,故D正确;
故选:AD。
14.火车转弯可近似看成是做匀速圆周运动,当火车速度提高时会使轨道的外轨受损。为解决火车高速转弯时不使外轨受损这一难题,你认为以下措施可行的是( )
A.适当增高内轨 B.适当增高外轨
C.减小弯道半径 D.增大弯道半径
【分析】火车转弯时需要向心力,若重力和轨道的弹力的合力恰好充当向心力,则内外轨道均不受侧压力;根据向心力公式可得出解决方案。
【解答】解:火车转弯时为减小外轨所受压力,可使外轨略高于内轨,若火车速度合适。此时,如图。
F=mgtanθ=m
得:v=;
设铁轨的宽度为d,两侧的高度差为h
所以:v≈
当火车速度增大时,应适当增大转弯半径或增加内外轨道的高度差;
故选:BD。
15.如图甲所示,用不可伸长的轻质细绳拴着一小球,在竖直面内做圆周运动2的图象如图乙所示,已知重力加速度g=10m/s2,下列说法正确的( )
A.小球运动到最高点的最小速度为1m/s
B.小球的质量为0.1kg
C.细绳长为0.2m
D.当小球在最高点的速度为m/s时,小球运动到最低点时细绳的拉力大小为7N
【分析】在最高点,根据牛顿第二定律得出F与v2的关系式,结合图线的斜率和截距求出当地的重力加速度和轻质绳长。根据动能定理和牛顿第二定律求出最低点拉力的表达式,结合最高点的拉力表达式求出拉力之差。
【解答】解:A、在最高点,弹力F为零时,故A正确;
B、根据F=m,则质量m=8.1kg;
C、在最高点有:F=m,代入F=6N,v2=2(m/s)7,解得L=0.1m,故C错误;
D、当最高点v=,设最低点的速度为v′mv′8﹣mv3,根据牛顿第二定律得:F′﹣mg=m,联立解得:F′=7N。
故选:ABD。
16.如图是某共享自行车的传动结构示意图,其中Ⅰ是半径为r1的牙盘(大齿轮),Ⅱ是半径为r2的飞轮(小齿轮),Ⅲ是半径为r3的后轮。若某人在匀速骑行时每秒踩脚踏板转n圈,则下列判断正确的是( )
A.牙盘转动角速度为
B.飞轮边缘转动线速度2πnr2
C.牙盘边缘上点的向心加速度为4π2n2r1
D.自行车匀速运动的速度为
【分析】转速的单位为转/秒,即单位时间做圆周运动转过的圈数,转过一圈对应的圆心角为2π,所以角速度ω=转速n×2π,由于大齿轮I和小齿轮II是通过链条传动,所以大小齿轮边缘上线速度大小相等,又小齿轮II和车轮III是同轴转动,所以它们角速度相等,要知道车轮边缘线速度的大小,则需要知道车轮的半径;利用I和II线速度大小相等,II和III角速度相等,列式求III的线速度大小即可。
【解答】解:A、某人在匀速骑行时每秒踩脚踏板转n圈,则牙盘的转动周期T=1==2πn;
B、根据题意知轮I和轮II边缘上的线速度的大小相等2ω8=r1ω1=5πnr1,故B错误;
C、牙盘边缘向心加速度为a1=ω82r1=6π2n2r6,故C正确;
D、轮II的角速度ω2=ω1,因为轮II和轮III共轴,所以转动的角速度相等3=ω3,
自行车匀速运动的速度等于轮III边缘的线速度,根据v=rω可知自行车匀速运动的速度v′=ω3r3=.故D正确。
故选:CD。
17.小球质量为m,用长为L的轻质细线悬挂在O点,在O点的正下方,把细线沿水平方向拉直,如图所示,当细线碰到钉子的瞬间,设线没有断裂( )
A.小球的角速度突然增大
B.小球的瞬时速度突然增大
C.小球的向心加速度突然增大
D.小球对悬线的拉力保持不变
【分析】把悬线沿水平方向拉直后无初速度释放,当悬线碰到钉子的前后瞬间,线速度大小不变,半径减小,根据v=rω、a=判断角速度、向心加速度大小的变化,根据牛顿第二定律判断悬线拉力的变化.
【解答】解:AB、把悬线沿水平方向拉直后无初速度释放,由于绳子拉力与重力都与速度垂直,即线速度大小不变,根据v=rω。故A正确。
C、当悬线碰到钉子后,线速度大小不变分析可知。故C正确。
D、根据牛顿第二定律得:T﹣mg=m得,r变小,则绳子的拉力T增大。
故选:AC。
三.解答题(共2小题)
18.近年,我国的高铁发展非常迅猛.为了保证行车安全,车辆转弯的技术要求是相当高的.如果在转弯处铺成如图所示内、外等高的轨道,火车的 外轨 (选填“外轮”、“内轮”)对轨道有侧向挤压,容易导致翻车事故.为此,铺设轨道时应该把 内轨 (选填“外轨”、“内轨”)适当降低一定的高度.如果两轨道间距为L,内外轨高度差为h,弯道半径为R .
【分析】火车拐弯需要有指向圆心的向心力,若内、外轨等高,则火车拐弯时由外轨的压力去提供,若火车拐弯时不侧向挤压车轮轮缘,要靠重力和支持力的合力提供向心力,进而判断降低哪一侧的高度.火车对内外轨轨道均无侧向挤压时,火车拐弯所需要的向心力由支持力和重力的合力提供.根据牛顿第二定律求解火车的行驶速度.
【解答】解:火车拐弯需要有指向圆心的向心力,若内,则火车拐弯时由外轨的压力去提供,若火车拐弯时不侧向挤压车轮轮缘,则铺设轨道时应该把内轨降低一定的高度.
设路面的倾角为θ,由牛顿第二定律得:mgtanθ=m
由于θ较小,则tanθ≈sinθ≈
解得 v=
故答案为:外轮,内轨,.
19.如图,支架质量为M,置于水平地面上.轴O处有一长为L的杆(质量不计),支架保持静止.若小球到达最高点时支架对地面的压力恰好为0,求,小球通过最高点速度的大小?
【分析】小球到达最高点时,恰好支架对地面无压力为零,说明杆对支架的拉力为Mg,则杆对小球的作用力为Mg,根据合外力提供小球圆周运动的向心力,根据牛顿第二定律列式求解小球通过最高点的速度.
【解答】解:设小球通过最高点时,杆子的拉力大小为F,
以M为研究对象,支架对地面无压力为零
以m为研究对象,由牛顿第二定律得:F+mg=m
由①②解得 v=
答:小球通过最高点速度的大小为.
第1页(共1页)
一.选择题(共12小题)
1.如图所示,在光滑水平面上,小球在拉力F作用下做匀速圆周运动,拉力F发生变化,则关于小球运动情况的说法正确的是( )
A.若拉力突然变小,小球将沿Pa做离心运动
B.若拉力突然变大,小球将沿Pb做离心运动
C.若拉力突然变小,小球将沿Pc做向心运动
D.若拉力突然消失,小球将沿Pa做匀速直线运动
2.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc C.Fc<Fa<Fb D.Fa>Fc>Fb
3.下列关于离心运动的叙述中不正确的是( )
A.离心运动是由于合力不足以提供向心力而引起的
B.离心运动的轨迹一定是直线
C.洗衣机的脱水筒是利用离心运动把湿衣服甩干的
D.汽车转弯时速度过大,会因离心运动造成交通事故
4.长度为L=0.5m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
A.6.0N的压力 B.6.0N的拉力 C.24N的压力 D.24N的拉力
5.一精确转动的机械手表,秒针的角速度大约为( )
A.0.05rad/s B.0.1rad/s C.1rad/s D.6rad/s
6.暗物质是二十一世纪物理学之谜,对该问题的研究可能带来一场物理学的革命.为了探测暗物质,我国在2015年12月17日成功发射了一颗被命名为“悟空”的暗物质探测卫星.已知“悟空”在低于同步卫星的轨道上绕地球做匀速圆周运动(t小于其运动周期),运动的弧长为s,与地球中心连线扫过的角度为β(弧度),则下列说法中正确的是( )
A.“悟空”的线速度大于第一宇宙速度
B.“悟空”的向心加速度小于地球同步卫星的向心加速度
C.“悟空”的环绕周期为
D.“悟空”的质量为
7.如图所示,两个质量相同的小球A、B,用长度之比为LA:LB=3:2的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的( )
A.角速度之比为ωA:ωB=3:2
B.线速度之比为vA:vB=1:1
C.向心力之比为FA:FB=2:3
D.悬线的拉力之比为TA:TB=3:2
8.如图所示,A、B两个物体与圆盘保持相对静止,随圆盘一起做匀速圆周运动( )
A.3个,5个 B.3个,4个 C.4个,5个 D.4个,6个
9.如图所示,将完全相同的两个小球A、B,用长L=0.8m的细绳悬于以v=4m/s向右匀速运动的小车顶部,由于某种原因,小车突然停止运动A:FB为(g=10m/s2)( )
A.1:1 B.2:1 C.3:1 D.4:1
10.如图所示,长为L的细轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,这样就构成了一个圆锥摆.不计空气阻力,关于小球受力( )
A.小球只受重力和向心力作用
B.小球只受重力和绳的拉力作用
C.小球只受重力、绳的拉力和向心力作用
D.小球只受重力、绳的拉力和离心力作用
11.将自行车转弯近似看成它绕某个定点O(图中未画出)做圆周运动。如图所示为自行车转弯过程中某时刻的俯视图,A点、B点分别为自行车前、后轮轴中心上的点,则A点和B点的( )
A.线速度相同
B.角速度相同
C.向心加速度相同
D.线速度、角速度和向心加速度都不同
12.如图所示,质量分别为2m和m的可视为质点的小物块A和B放在粗糙的水平转台上,其离转轴的距离均为r,忽略空气阻力的影响,设最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A.若转速缓慢增加,小物块B先相对转台滑动
B.在小物块均未相对转台滑动前,A的向心加速度比B大
C.在小物块均未相对转台滑动前,A和B所受摩擦力大小相等
D.A、B两个小物块即将相对转台滑动的最大角速度ω均等于
二.多选题(共5小题)
13.以下措施或者行为是为了防止离心运动的是( )
A.游乐场所中空中转椅的安全卡扣
B.转动雨伞甩掉伞上的水
C.运动员将链球甩出去
D.弯道公路的限速标志
14.火车转弯可近似看成是做匀速圆周运动,当火车速度提高时会使轨道的外轨受损。为解决火车高速转弯时不使外轨受损这一难题,你认为以下措施可行的是( )
A.适当增高内轨 B.适当增高外轨
C.减小弯道半径 D.增大弯道半径
15.如图甲所示,用不可伸长的轻质细绳拴着一小球,在竖直面内做圆周运动2的图象如图乙所示,已知重力加速度g=10m/s2,下列说法正确的( )
A.小球运动到最高点的最小速度为1m/s
B.小球的质量为0.1kg
C.细绳长为0.2m
D.当小球在最高点的速度为m/s时,小球运动到最低点时细绳的拉力大小为7N
16.如图是某共享自行车的传动结构示意图,其中Ⅰ是半径为r1的牙盘(大齿轮),Ⅱ是半径为r2的飞轮(小齿轮),Ⅲ是半径为r3的后轮。若某人在匀速骑行时每秒踩脚踏板转n圈,则下列判断正确的是( )
A.牙盘转动角速度为
B.飞轮边缘转动线速度2πnr2
C.牙盘边缘上点的向心加速度为4π2n2r1
D.自行车匀速运动的速度为
17.小球质量为m,用长为L的轻质细线悬挂在O点,在O点的正下方,把细线沿水平方向拉直,如图所示,当细线碰到钉子的瞬间,设线没有断裂( )
A.小球的角速度突然增大
B.小球的瞬时速度突然增大
C.小球的向心加速度突然增大
D.小球对悬线的拉力保持不变
三.解答题(共2小题)
18.近年,我国的高铁发展非常迅猛.为了保证行车安全,车辆转弯的技术要求是相当高的.如果在转弯处铺成如图所示内、外等高的轨道,火车的 (选填“外轮”、“内轮”)对轨道有侧向挤压,容易导致翻车事故.为此,铺设轨道时应该把 (选填“外轨”、“内轨”)适当降低一定的高度.如果两轨道间距为L,内外轨高度差为h,弯道半径为R .
19.如图,支架质量为M,置于水平地面上.轴O处有一长为L的杆(质量不计),支架保持静止.若小球到达最高点时支架对地面的压力恰好为0,求,小球通过最高点速度的大小?
人教版(2019)必修第二册《第6章 圆周运动》2021年单元测试卷(3)
参考答案与试题解析
一.选择题(共12小题)
1.如图所示,在光滑水平面上,小球在拉力F作用下做匀速圆周运动,拉力F发生变化,则关于小球运动情况的说法正确的是( )
A.若拉力突然变小,小球将沿Pa做离心运动
B.若拉力突然变大,小球将沿Pb做离心运动
C.若拉力突然变小,小球将沿Pc做向心运动
D.若拉力突然消失,小球将沿Pa做匀速直线运动
【分析】本题考查离心现象产生原因以及运动轨迹,当向心力突然消失或变小时,物体会做离心运动,运动轨迹可是直线也可以是曲线,要根据受力情况分析.
【解答】解:在水平面上,细绳的拉力提供m所需的向心力,物体所受合力为零。若拉力减小时,拉力增大时,故D正确。
故选:D。
2.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc C.Fc<Fa<Fb D.Fa>Fc>Fb
【分析】由图象知轨道半径大小关系,根据向心力公式F=m比较向心力的大小。
【解答】解:根据向心力公式F=m知v大小相等,向心力越小a>rb>rc,所以Fa<Fb<Fc,故B正确,ACD错误。
故选:B。
3.下列关于离心运动的叙述中不正确的是( )
A.离心运动是由于合力不足以提供向心力而引起的
B.离心运动的轨迹一定是直线
C.洗衣机的脱水筒是利用离心运动把湿衣服甩干的
D.汽车转弯时速度过大,会因离心运动造成交通事故
【分析】当物体受到的合力的大小不足以提供物体所需要的向心力的大小时,物体就要远离圆心,此时物体做的就是离心运动.
【解答】解:AB、当外界提供的向心力突然消失时,物体就要远离圆心,但轨迹不一定是直线,B错误;
C、水滴依附的附着力是一定的,水滴被甩掉;
D、在水平面拐弯、支持力,重力和支持力平衡,由于最大静摩擦力一定,使静摩擦力小于向心力,容易造成事故。
本题选错误的,
故选:B。
4.长度为L=0.5m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
A.6.0N的压力 B.6.0N的拉力 C.24N的压力 D.24N的拉力
【分析】小球在细杆的作用下,在竖直平面内做圆周运动。对最高点受力分析,找出提供向心力的来源,结合已知量可求出最高点小球速率为2m/s时的细杆受到的力。
【解答】解:小球以O点为圆心在竖直平面内做圆周运动,当在最高点小球与细杆无弹力作用时1,则有:
mg=m
得:v1==m/s
由于v7=m/s>2m/s,小球在O点受力分析,有:
mg﹣F支=m
则有:F支=mg﹣m=30N﹣3
所以细杆受到的压力,大小为7N。
故选:A。
5.一精确转动的机械手表,秒针的角速度大约为( )
A.0.05rad/s B.0.1rad/s C.1rad/s D.6rad/s
【分析】角速度是描述物体转动快慢的物理量,加速度ω==
【解答】解:秒针转动一圈的时间为60s,角速度ω==。
故选:B。
6.暗物质是二十一世纪物理学之谜,对该问题的研究可能带来一场物理学的革命.为了探测暗物质,我国在2015年12月17日成功发射了一颗被命名为“悟空”的暗物质探测卫星.已知“悟空”在低于同步卫星的轨道上绕地球做匀速圆周运动(t小于其运动周期),运动的弧长为s,与地球中心连线扫过的角度为β(弧度),则下列说法中正确的是( )
A.“悟空”的线速度大于第一宇宙速度
B.“悟空”的向心加速度小于地球同步卫星的向心加速度
C.“悟空”的环绕周期为
D.“悟空”的质量为
【分析】已知该太空电站经过时间t(t小于太空电站运行的周期),它运动的弧长为s,它与地球中心连线扫过的角度为β(弧度),根据线速度和角速度定义可求得太空站的线速度和角速度,然后根据v=ωr可求得轨道半径;根据万有引力提供向心力求求得地球的质量.
【解答】解:A、该太空电站经过时间t(t小于太空电站运行的周期),它与地球中心连线扫过的角度为β(弧度),
则太空站运行的线速度为 v=
角速度为:ω=
根据v=ωr得轨道半径为:r==
人类第一台太空电站在地球的同步轨道上绕地球做匀速圆周运动,万有引力提供向心力=m,可知卫星的轨道半径越大,第一宇宙速度是近地卫星的环绕速度,故A错误;
B、由G,则知“悟空”的向心加速度大于地球同步卫星的向心加速度。
C、“悟空”的环绕周期为T==;
D、“悟空”绕地球做匀速圆周运动,即:G2,ω=
联立解得:地球的质量为 M=,不能求出“悟空”的质量;
故选:C。
7.如图所示,两个质量相同的小球A、B,用长度之比为LA:LB=3:2的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的( )
A.角速度之比为ωA:ωB=3:2
B.线速度之比为vA:vB=1:1
C.向心力之比为FA:FB=2:3
D.悬线的拉力之比为TA:TB=3:2
【分析】根据小球重力和拉力的合力提供向心力得出角速度的表达式,得出角速度之比,从而得出线速度之比。根据平行四边形定则求出拉力的表达式,从而得出拉力之比。
【解答】解:A、小球靠重力和拉力的合力提供向心力,mgtanθ=mLsinθ ω2,则ω=,由于两球做圆周运动悬点到圆心的距离相等,故A错误。
B、由A选项知,根据v=rω=Lsinθ ω知,则线速度之比不等于1:4。
C、向心力F=mgtanθ,A、B悬线与竖直方向的夹角的余弦之比为2:3,可知向心力之比不等于6:3。
D、悬线拉力T=、B悬线与竖直方向的夹角的余弦之比为2:8A:TB=3:2,故D正确。
故选:D。
8.如图所示,A、B两个物体与圆盘保持相对静止,随圆盘一起做匀速圆周运动( )
A.3个,5个 B.3个,4个 C.4个,5个 D.4个,6个
【分析】分别对A与B进行受力分析即可,要注意向心力是根据效果命名的力,只能由其它力的合力或者分力来充当,不是真实存在的力,不能说物体受到向心力。
【解答】解:A物体在水平面内做匀速圆周运动,一定受到重力和B对A的支持力作用,有背离圆心的运动趋势,且静摩擦力提供向心力;
B物体也在水平面内做匀速圆周运动,一定受到重力和圆盘的支持力作用;物体在转动过程中,因此受到指向圆心的静摩擦力,两个静摩擦力的合力提供向心力。故A正确
故选:A。
9.如图所示,将完全相同的两个小球A、B,用长L=0.8m的细绳悬于以v=4m/s向右匀速运动的小车顶部,由于某种原因,小车突然停止运动A:FB为(g=10m/s2)( )
A.1:1 B.2:1 C.3:1 D.4:1
【分析】小车原来向右匀速运动,突然停止运动时,A球由于惯性,会向前摆动,将做圆周运动,B球受到小车前壁的作用停止运动,在竖直方向上拉力等于重力,根据牛顿第二定律求出A球绳的拉力,从而求出两悬线的拉力之比。
【解答】解:若A、B的质量为m,则
对A球有:FA﹣mg=m,得FA=mg+m=m(10+。
对B球有:FB=mg=10m。
所以FA:FB=3:1.故C正确,A、B。
故选:C。
10.如图所示,长为L的细轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,这样就构成了一个圆锥摆.不计空气阻力,关于小球受力( )
A.小球只受重力和向心力作用
B.小球只受重力和绳的拉力作用
C.小球只受重力、绳的拉力和向心力作用
D.小球只受重力、绳的拉力和离心力作用
【分析】分析小球的受力,受到重力、绳的拉力,二者的合力提供向心力,向心力是效果力,不是重复受力.
【解答】解:小球做匀速圆周运动,合力不为零,提供向心力;
小球受重力和细线的拉力,共2个力,对惯性系没有离心力的说法;
故ACD错误,B正确;
故选:B。
11.将自行车转弯近似看成它绕某个定点O(图中未画出)做圆周运动。如图所示为自行车转弯过程中某时刻的俯视图,A点、B点分别为自行车前、后轮轴中心上的点,则A点和B点的( )
A.线速度相同
B.角速度相同
C.向心加速度相同
D.线速度、角速度和向心加速度都不同
【分析】首先根据A、B绕着同一个点转动,得到A、B两点具有相同的角速度;然后利用公式v=ωr和a=ω2r判断A点和B点线速度和向心加速度是否相同。
【解答】解:B、因为A,所以具有相同的角速度;
A、由v=ωr可知当角速度相等时,线速度也不同;
C、由a=ω2r可知当角速度相等时,转动的半径不同时,故C错误;
D、由上述分析可知A点和B点的角速度相同,故D错误。
故选:B。
12.如图所示,质量分别为2m和m的可视为质点的小物块A和B放在粗糙的水平转台上,其离转轴的距离均为r,忽略空气阻力的影响,设最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
A.若转速缓慢增加,小物块B先相对转台滑动
B.在小物块均未相对转台滑动前,A的向心加速度比B大
C.在小物块均未相对转台滑动前,A和B所受摩擦力大小相等
D.A、B两个小物块即将相对转台滑动的最大角速度ω均等于
【分析】当角速度较小时,A、B均靠静摩擦力提供向心力,角速度增大,达到最大静摩擦力,由向心力公式即可求出临界角速度。
【解答】解:AD、对物块受力分析可知,f=mω2r,当f达到最大静摩擦力时,根据牛顿第二定律得:μmg=mrω2,解得A、B两个小物块即将相对转台滑动的最大角速度ω为:ω=,只与物块的转动半径和动摩擦因数有关,两物块一起相对转台滑动,D正确;
B、在小物块均未相对转台滑动前,可知a=ω6r,故A的向心加速度与B的向心加速度大小相等,故B错误;
C、在小物块均未相对转台滑动前2r,可知A和B所受摩擦力大小与质量成正比,故C错误;
故选:D。
二.多选题(共5小题)
13.以下措施或者行为是为了防止离心运动的是( )
A.游乐场所中空中转椅的安全卡扣
B.转动雨伞甩掉伞上的水
C.运动员将链球甩出去
D.弯道公路的限速标志
【分析】当物体提供的力小于所需的向心力,做离心运动,当物体提供的力大于所需的向心力,做近心运动.
【解答】解:A、空中转椅的安全卡扣是为了防止游人被甩出做离心运动而设计的;
B、转动雨伞时,故B错误;
C、运动员将链球甩出去也是利用了链球的离心运动;
D、弯道公路的限速标志是提醒汽车减速至限速以下的速度,故D正确;
故选:AD。
14.火车转弯可近似看成是做匀速圆周运动,当火车速度提高时会使轨道的外轨受损。为解决火车高速转弯时不使外轨受损这一难题,你认为以下措施可行的是( )
A.适当增高内轨 B.适当增高外轨
C.减小弯道半径 D.增大弯道半径
【分析】火车转弯时需要向心力,若重力和轨道的弹力的合力恰好充当向心力,则内外轨道均不受侧压力;根据向心力公式可得出解决方案。
【解答】解:火车转弯时为减小外轨所受压力,可使外轨略高于内轨,若火车速度合适。此时,如图。
F=mgtanθ=m
得:v=;
设铁轨的宽度为d,两侧的高度差为h
所以:v≈
当火车速度增大时,应适当增大转弯半径或增加内外轨道的高度差;
故选:BD。
15.如图甲所示,用不可伸长的轻质细绳拴着一小球,在竖直面内做圆周运动2的图象如图乙所示,已知重力加速度g=10m/s2,下列说法正确的( )
A.小球运动到最高点的最小速度为1m/s
B.小球的质量为0.1kg
C.细绳长为0.2m
D.当小球在最高点的速度为m/s时,小球运动到最低点时细绳的拉力大小为7N
【分析】在最高点,根据牛顿第二定律得出F与v2的关系式,结合图线的斜率和截距求出当地的重力加速度和轻质绳长。根据动能定理和牛顿第二定律求出最低点拉力的表达式,结合最高点的拉力表达式求出拉力之差。
【解答】解:A、在最高点,弹力F为零时,故A正确;
B、根据F=m,则质量m=8.1kg;
C、在最高点有:F=m,代入F=6N,v2=2(m/s)7,解得L=0.1m,故C错误;
D、当最高点v=,设最低点的速度为v′mv′8﹣mv3,根据牛顿第二定律得:F′﹣mg=m,联立解得:F′=7N。
故选:ABD。
16.如图是某共享自行车的传动结构示意图,其中Ⅰ是半径为r1的牙盘(大齿轮),Ⅱ是半径为r2的飞轮(小齿轮),Ⅲ是半径为r3的后轮。若某人在匀速骑行时每秒踩脚踏板转n圈,则下列判断正确的是( )
A.牙盘转动角速度为
B.飞轮边缘转动线速度2πnr2
C.牙盘边缘上点的向心加速度为4π2n2r1
D.自行车匀速运动的速度为
【分析】转速的单位为转/秒,即单位时间做圆周运动转过的圈数,转过一圈对应的圆心角为2π,所以角速度ω=转速n×2π,由于大齿轮I和小齿轮II是通过链条传动,所以大小齿轮边缘上线速度大小相等,又小齿轮II和车轮III是同轴转动,所以它们角速度相等,要知道车轮边缘线速度的大小,则需要知道车轮的半径;利用I和II线速度大小相等,II和III角速度相等,列式求III的线速度大小即可。
【解答】解:A、某人在匀速骑行时每秒踩脚踏板转n圈,则牙盘的转动周期T=1==2πn;
B、根据题意知轮I和轮II边缘上的线速度的大小相等2ω8=r1ω1=5πnr1,故B错误;
C、牙盘边缘向心加速度为a1=ω82r1=6π2n2r6,故C正确;
D、轮II的角速度ω2=ω1,因为轮II和轮III共轴,所以转动的角速度相等3=ω3,
自行车匀速运动的速度等于轮III边缘的线速度,根据v=rω可知自行车匀速运动的速度v′=ω3r3=.故D正确。
故选:CD。
17.小球质量为m,用长为L的轻质细线悬挂在O点,在O点的正下方,把细线沿水平方向拉直,如图所示,当细线碰到钉子的瞬间,设线没有断裂( )
A.小球的角速度突然增大
B.小球的瞬时速度突然增大
C.小球的向心加速度突然增大
D.小球对悬线的拉力保持不变
【分析】把悬线沿水平方向拉直后无初速度释放,当悬线碰到钉子的前后瞬间,线速度大小不变,半径减小,根据v=rω、a=判断角速度、向心加速度大小的变化,根据牛顿第二定律判断悬线拉力的变化.
【解答】解:AB、把悬线沿水平方向拉直后无初速度释放,由于绳子拉力与重力都与速度垂直,即线速度大小不变,根据v=rω。故A正确。
C、当悬线碰到钉子后,线速度大小不变分析可知。故C正确。
D、根据牛顿第二定律得:T﹣mg=m得,r变小,则绳子的拉力T增大。
故选:AC。
三.解答题(共2小题)
18.近年,我国的高铁发展非常迅猛.为了保证行车安全,车辆转弯的技术要求是相当高的.如果在转弯处铺成如图所示内、外等高的轨道,火车的 外轨 (选填“外轮”、“内轮”)对轨道有侧向挤压,容易导致翻车事故.为此,铺设轨道时应该把 内轨 (选填“外轨”、“内轨”)适当降低一定的高度.如果两轨道间距为L,内外轨高度差为h,弯道半径为R .
【分析】火车拐弯需要有指向圆心的向心力,若内、外轨等高,则火车拐弯时由外轨的压力去提供,若火车拐弯时不侧向挤压车轮轮缘,要靠重力和支持力的合力提供向心力,进而判断降低哪一侧的高度.火车对内外轨轨道均无侧向挤压时,火车拐弯所需要的向心力由支持力和重力的合力提供.根据牛顿第二定律求解火车的行驶速度.
【解答】解:火车拐弯需要有指向圆心的向心力,若内,则火车拐弯时由外轨的压力去提供,若火车拐弯时不侧向挤压车轮轮缘,则铺设轨道时应该把内轨降低一定的高度.
设路面的倾角为θ,由牛顿第二定律得:mgtanθ=m
由于θ较小,则tanθ≈sinθ≈
解得 v=
故答案为:外轮,内轨,.
19.如图,支架质量为M,置于水平地面上.轴O处有一长为L的杆(质量不计),支架保持静止.若小球到达最高点时支架对地面的压力恰好为0,求,小球通过最高点速度的大小?
【分析】小球到达最高点时,恰好支架对地面无压力为零,说明杆对支架的拉力为Mg,则杆对小球的作用力为Mg,根据合外力提供小球圆周运动的向心力,根据牛顿第二定律列式求解小球通过最高点的速度.
【解答】解:设小球通过最高点时,杆子的拉力大小为F,
以M为研究对象,支架对地面无压力为零
以m为研究对象,由牛顿第二定律得:F+mg=m
由①②解得 v=
答:小球通过最高点速度的大小为.
第1页(共1页)
