人教版(2019)必修第二册《第6章+圆周运动》2021年单元测试卷(4word版含答案)
文档属性
| 名称 | 人教版(2019)必修第二册《第6章+圆周运动》2021年单元测试卷(4word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 216.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-01 05:57:19 | ||
图片预览




文档简介
人教版(2019)必修第二册《第6章 圆周运动》2021年单元测试卷(4)
一.选择题(共12小题)
1.如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,管道内侧壁半径为R,则下列说法中正确的是( )
A.小球通过最高点时的最小速度vmin=
B.小球通过最高点时的最小速度vmin=0 m/s
C.小球在水平线ab以下的管道中运动时,内侧管壁对小球一定有作用力
D.小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力
2.下列生活中的一些现象是利用到了离心运动的是( )
A.驾驶汽车时必须系安全带
B.汽车过凹形路面时必须减速
C.火车轨道外高内低
D.洗衣机的脱水桶
3.如图所示,长为L的细轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,这样就构成了一个圆锥摆.不计空气阻力,关于小球受力( )
A.小球只受重力和向心力作用
B.小球只受重力和绳的拉力作用
C.小球只受重力、绳的拉力和向心力作用
D.小球只受重力、绳的拉力和离心力作用
4.如图所示,一圆柱形容器绕其轴线匀速转动,内部有A、B两个物体(A、B与容器接触面间仍相对静止),下列说法正确的是( )
A.两物体受到的摩擦力都增大
B.两物体受到的摩擦力大小都不变
C.物体A受到的摩擦力增大,物体B受到的摩擦力大小不变
D.物体A受到的摩擦力大小不变,物体B受到的摩擦力增大
5.一精确转动的机械手表,秒针的角速度大约为( )
A.0.05rad/s B.0.1rad/s C.1rad/s D.6rad/s
6.下列说法中正确的是( )
A.变速运动不一定都是曲线运动,曲线运动一定都是变速运动
B.平抛运动的物体每秒内速度大小的增量相等
C.匀速圆周运动的物体线速度保持不变
D.圆周运动的物体加速度一定指向圆心
7.如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a和b是轮边缘上的两个点( )
A.角速度大小相同 B.线速度大小相同
C.周期大小不同 D.转速大小不同
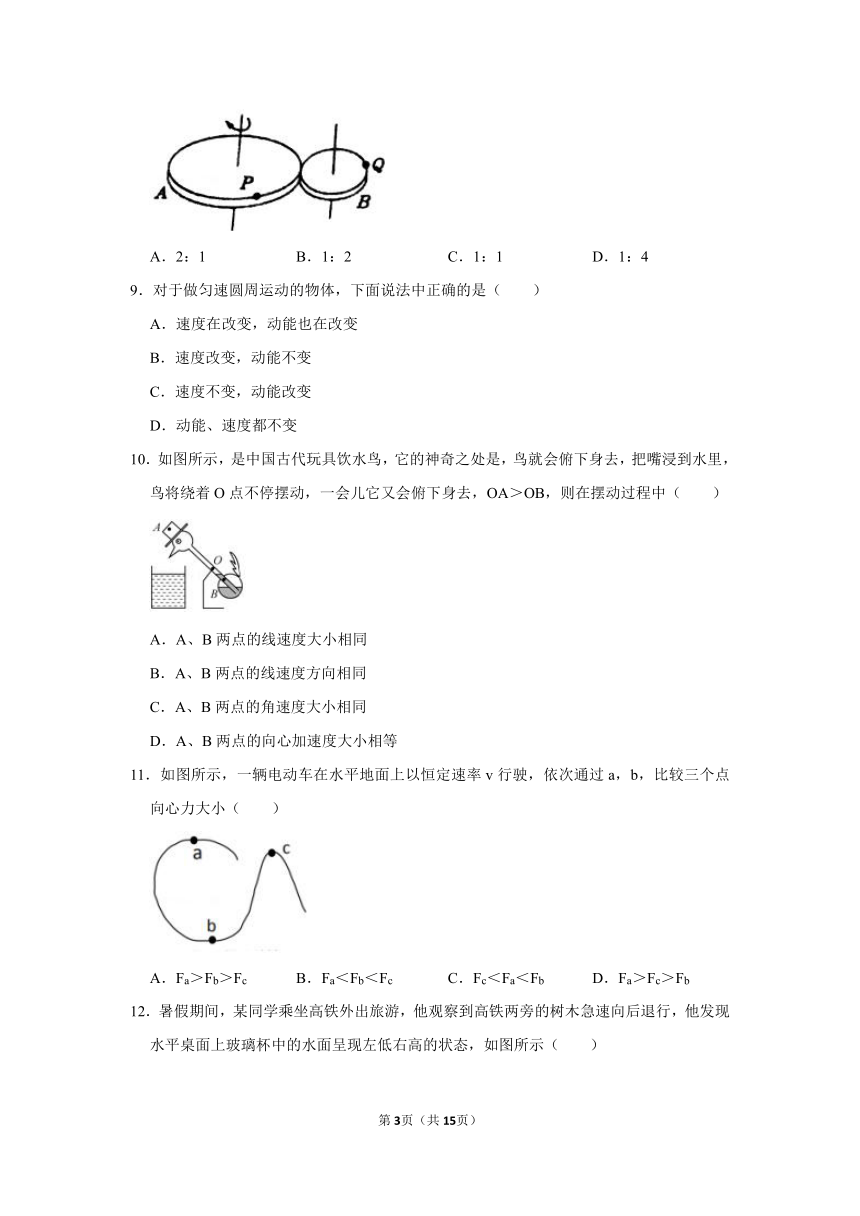
8.如图所示,A、B两轮属于摩擦传动,两轮半径RA=2RB,P、Q为两轮边缘上的点,当主动轮A匀速转动时,P、Q两点角速度大小之比为( )
A.2:1 B.1:2 C.1:1 D.1:4
9.对于做匀速圆周运动的物体,下面说法中正确的是( )
A.速度在改变,动能也在改变
B.速度改变,动能不变
C.速度不变,动能改变
D.动能、速度都不变
10.如图所示,是中国古代玩具饮水鸟,它的神奇之处是,鸟就会俯下身去,把嘴浸到水里,鸟将绕着O点不停摆动,一会儿它又会俯下身去,OA>OB,则在摆动过程中( )
A.A、B两点的线速度大小相同
B.A、B两点的线速度方向相同
C.A、B两点的角速度大小相同
D.A、B两点的向心加速度大小相等
11.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc C.Fc<Fa<Fb D.Fa>Fc>Fb
12.暑假期间,某同学乘坐高铁外出旅游,他观察到高铁两旁的树木急速向后退行,他发现水平桌面上玻璃杯中的水面呈现左低右高的状态,如图所示( )
A.加速行驶 B.减速行驶 C.向右转弯 D.向左转弯
二.多选题(共5小题)
13.如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带不打滑( )
A.A、B、C三点的加速度之比aA:aB:aC=6:2:1
B.A、B、C三点的线速度大小之比vA:vB:vC=3:2:2
C.A、B、C三点的角速度之比ωA:ωB:ωC=2:2:1
D.A、B、C三点的周期之比TA:TB:TC=1:1:2
14.长为L的轻杆,一端固定一个小球,以另一端O为圆心,关于小球在最高点的速度v下列说法中正确的是( )
A.当v的值小于时,杆对小球的弹力指向圆心
B.当v由逐渐增大,杆对小球的拉力逐渐增大
C.当v由逐渐减小时,杆对小球的支持力逐渐减小
D.当v由零逐渐增大时,向心力也逐渐增大
15.一个小球以大小为a=4m/s2的向心加速度做匀速圆周运动,半径R=1m,则下列说法正确的是( )
A.小球运动的角速度为2rad/s
B.小球做圆周运动的周期为πs
C.小球在t=s内通过的位移大小为m
D.小球在πs内通过的路程为零
16.一圆周半径为R,质点沿着这个圆周运动,当它通过1,设此过程中的最大位移的大小为x,则以下说法正确的是( )
A.θ=90° B.θ=450° C.x=R D.x=2R
17.关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀速运动
B.匀速圆周运动是匀变速运动
C.匀速圆周运动是匀速率圆周运动
D.在任意相等的时间内通过的路程相等
三.解答题(共2小题)
18.如图所示,半径为0.1m的轻滑轮,通过绕在其上面的细线与重物相连2的加速度匀加速下落,则当它下落高度为1 m时的瞬时速度是多大?此刻的滑轮转动的角速度是多大?
19.如图是一行星绕恒星做匀速圆周运动的示意图,由天文观测可得其运行周期为T,速度为v,试求:
(1)行星运动的轨道半径R;
(2)行星运动的加速度a;
(3)恒星的质量M.
人教版(2019)必修第二册《第6章 圆周运动》2021年单元测试卷(4)
参考答案与试题解析
一.选择题(共12小题)
1.如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,管道内侧壁半径为R,则下列说法中正确的是( )
A.小球通过最高点时的最小速度vmin=
B.小球通过最高点时的最小速度vmin=0 m/s
C.小球在水平线ab以下的管道中运动时,内侧管壁对小球一定有作用力
D.小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力
【分析】小球在竖直光滑圆形管道内做圆周运动,在最高点,由于外管或内管都可以对小球产生弹力作用,从而可以确定在最高点的最小速度.小球做圆周运动时,沿半径方向的合力提供做圆周运动的向心力.
【解答】解:A、在最高点,当小球的速度等于0时,大小为mg.故A错误。
C、小球在水平线ab以下管道运动,所以外侧管壁对小球一定有作用力。故C错误。
D、小球在水平线ab以上管道运动,当速度较大时,此时外侧管壁有作用力,内侧管壁有作用力。
故选:B。
2.下列生活中的一些现象是利用到了离心运动的是( )
A.驾驶汽车时必须系安全带
B.汽车过凹形路面时必须减速
C.火车轨道外高内低
D.洗衣机的脱水桶
【分析】驾驶汽车时必须系安全带是为了避免惯性带来的伤害;汽车过凹形路面时必须减速是为了防止爆胎;火车轨道外高内低是防止与轨道挤压;洗衣机的脱水桶是利用了离心运动。
【解答】解:A、驾驶汽车时必须系安全带是为了避免惯性带来的伤害;
B、汽车过凹形路面时必须减速是为了防止爆胎;
C、火车轨道外高内低是防止与轨道挤压;
D、洗衣机的脱水桶是利用了离心运动。
故选:D。
3.如图所示,长为L的细轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,这样就构成了一个圆锥摆.不计空气阻力,关于小球受力( )
A.小球只受重力和向心力作用
B.小球只受重力和绳的拉力作用
C.小球只受重力、绳的拉力和向心力作用
D.小球只受重力、绳的拉力和离心力作用
【分析】分析小球的受力,受到重力、绳的拉力,二者的合力提供向心力,向心力是效果力,不是重复受力.
【解答】解:小球做匀速圆周运动,合力不为零,提供向心力;
小球受重力和细线的拉力,共2个力,对惯性系没有离心力的说法;
故ACD错误,B正确;
故选:B。
4.如图所示,一圆柱形容器绕其轴线匀速转动,内部有A、B两个物体(A、B与容器接触面间仍相对静止),下列说法正确的是( )
A.两物体受到的摩擦力都增大
B.两物体受到的摩擦力大小都不变
C.物体A受到的摩擦力增大,物体B受到的摩擦力大小不变
D.物体A受到的摩擦力大小不变,物体B受到的摩擦力增大
【分析】分别对物体A、B受力分析,根据牛顿第二定律和共点力平衡即可判断摩擦力的变化。
【解答】解:对A分析,A在竖直方向受力平衡1=mg,故转速增大后摩擦力不变;
对B分析,B受到的摩擦力提供向心力2=m(6πn)2r,由于转速增大,故ABC错误;
故选:D。
5.一精确转动的机械手表,秒针的角速度大约为( )
A.0.05rad/s B.0.1rad/s C.1rad/s D.6rad/s
【分析】角速度是描述物体转动快慢的物理量,加速度ω==
【解答】解:秒针转动一圈的时间为60s,角速度ω==。
故选:B。
6.下列说法中正确的是( )
A.变速运动不一定都是曲线运动,曲线运动一定都是变速运动
B.平抛运动的物体每秒内速度大小的增量相等
C.匀速圆周运动的物体线速度保持不变
D.圆周运动的物体加速度一定指向圆心
【分析】曲线运动的速度方向时刻变化,为变速运动,但变速运动并不一定为曲线运动,可能为变速直线运动,平抛运动为加速度恒定的匀变速曲线运动,匀速圆周运动是速率不变的圆周运动,匀速圆周运动的向心加速度指向圆心,但变速圆周运动的加速度不指向圆心。
【解答】解:A、曲线运动的瞬时速度方向时刻发生改变,但变速运动有可能是变速直线运动;
B、平抛运动匀变速曲线运动,每秒内速度的增量△v=g△t=10m/s,但每秒内速度的大小增量不等;
C、匀速圆周运动线速度方向时刻发生改变,故C错误;
D、只有匀速圆周运动加速度指向圆心,故D错误
故选:A。
7.如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a和b是轮边缘上的两个点( )
A.角速度大小相同 B.线速度大小相同
C.周期大小不同 D.转速大小不同
【分析】a、b两点共轴转动,角速度相等,则周期与转速相等,根据转动半径的大小比较线速度的大小即可.
【解答】解:A、D、a、b两点共轴转动,转速相等,D错误;
B、由于转动的半径不等,线速度大小不等;
C、根据T=,a,则周期一定相等。
故选:A。
8.如图所示,A、B两轮属于摩擦传动,两轮半径RA=2RB,P、Q为两轮边缘上的点,当主动轮A匀速转动时,P、Q两点角速度大小之比为( )
A.2:1 B.1:2 C.1:1 D.1:4
【分析】A和B靠摩擦传动,边缘上各点的线速度相同,根据线速度角速度关系可得出角速度的关系。
【解答】解:A、B两轮靠轮边缘间的摩擦转动,
由v=ωR可知:线速度相等时,角速度与半径成反比
ωA:ωB=RB:RA=1:2,即P,故B正确。
故选:B。
9.对于做匀速圆周运动的物体,下面说法中正确的是( )
A.速度在改变,动能也在改变
B.速度改变,动能不变
C.速度不变,动能改变
D.动能、速度都不变
【分析】速度是矢量,有大小有方向,要保持不变,大小和方向都不变.在匀速圆周运动的过程中,速度的方向时刻改变,所以速度变化,动能是标量,不发生改变.
【解答】解:匀速圆周运动的过程中,线速度的大小不变,所以线速度改变,不发生改变。
故选:B。
10.如图所示,是中国古代玩具饮水鸟,它的神奇之处是,鸟就会俯下身去,把嘴浸到水里,鸟将绕着O点不停摆动,一会儿它又会俯下身去,OA>OB,则在摆动过程中( )
A.A、B两点的线速度大小相同
B.A、B两点的线速度方向相同
C.A、B两点的角速度大小相同
D.A、B两点的向心加速度大小相等
【分析】A、B两点属于同轴转动的模型,同轴转动角速度相等,根据v=ωr,a=ω2r分析线速度和加速度。
【解答】解:C、根据同轴转动角速度相等知,A,故C正确。
AB、根据v=ωr知A点半径大,线速度方向就是该点的运动方向,故AB错误。
D、根据a=ω2r知A点半径大,加速度较大。
故选:C。
11.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc C.Fc<Fa<Fb D.Fa>Fc>Fb
【分析】由图象知轨道半径大小关系,根据向心力公式F=m比较向心力的大小。
【解答】解:根据向心力公式F=m知v大小相等,向心力越小a>rb>rc,所以Fa<Fb<Fc,故B正确,ACD错误。
故选:B。
12.暑假期间,某同学乘坐高铁外出旅游,他观察到高铁两旁的树木急速向后退行,他发现水平桌面上玻璃杯中的水面呈现左低右高的状态,如图所示( )
A.加速行驶 B.减速行驶 C.向右转弯 D.向左转弯
【分析】水面上有一个质量为m的水滴,分析该水滴受到的合外力方向,由此进行判断。
【解答】解:设水面上有一个质量为m的水滴,受到重力和周围水对它的作用力
说明该水滴受到的合外力方向向左,相对于该同学来说,故D正确。
故选:D。
二.多选题(共5小题)
13.如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带不打滑( )
A.A、B、C三点的加速度之比aA:aB:aC=6:2:1
B.A、B、C三点的线速度大小之比vA:vB:vC=3:2:2
C.A、B、C三点的角速度之比ωA:ωB:ωC=2:2:1
D.A、B、C三点的周期之比TA:TB:TC=1:1:2
【分析】靠传送带传动的两个轮子边缘上各点的线速度大小相等,共轴转动的各点,角速度相等。B点和C点具有相同的线速度,A点和B点具有相同的角速度。根据v=rω,求出三点的角速度之比和线速度之比。根据a=ωv求解加速度之比,根据T=求解周期之比。
【解答】解:C、B点和C点具有相同大小的线速度,知B,所以ωB:ωC=rC:rB=2:1.而A点和B点具有相同的角速度A:ωB:ωC=6:2:1.故C正确;
B、根据v=rω,所以vA:vB:=5:1.BC线速度相等A:vB:vC=3:8:1.故B错误
A、根据a=vω得:aA:aB:aC=vAωA:aB:vBωB:vCωC=6:3:1.故A正确;
D、根据T=A:TB:TC==6:1:2。
故选:ACD。
14.长为L的轻杆,一端固定一个小球,以另一端O为圆心,关于小球在最高点的速度v下列说法中正确的是( )
A.当v的值小于时,杆对小球的弹力指向圆心
B.当v由逐渐增大,杆对小球的拉力逐渐增大
C.当v由逐渐减小时,杆对小球的支持力逐渐减小
D.当v由零逐渐增大时,向心力也逐渐增大
【分析】当速度v=,小球靠重力提供向心力,杆子的作用力为零;若,杆子表现为支持力,若v,杆子表现为拉力,结合牛顿第二定律分析判断.
【解答】解:A、在最高点,小球靠重力提供向心力,若v,即杆对小球的弹力方向背离圆心。
B、当v由,杆子表现为拉力,速度增大,故B正确。
C、当v由,杆子表现为支持力,速度减小,故C错误。
D、根据知,向心力增大。
故选:BD。
15.一个小球以大小为a=4m/s2的向心加速度做匀速圆周运动,半径R=1m,则下列说法正确的是( )
A.小球运动的角速度为2rad/s
B.小球做圆周运动的周期为πs
C.小球在t=s内通过的位移大小为m
D.小球在πs内通过的路程为零
【分析】依据a=ω2r可得角速度,根据求周期,根据V=ωr求线速度,根据l=vt求路程.
【解答】解:A、ω==,故A正确;
B、周期T=,故B正确;
C、根据V=ωr,t==m,故C错误;
D、小球在πs内通过的路程为l=vt=2×π=2π;
故选:AB。
16.一圆周半径为R,质点沿着这个圆周运动,当它通过1,设此过程中的最大位移的大小为x,则以下说法正确的是( )
A.θ=90° B.θ=450° C.x=R D.x=2R
【分析】根据圆周运动的规律可明确转过的角度,再根据位移的定义由几何关系即可求出最大位移.
【解答】解:A、做圆周运动的物体每转动一周,故通过1=450°,B正确;
C、此时物体从起点又转动了周R;故C正确;
故选:BC。
17.关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀速运动
B.匀速圆周运动是匀变速运动
C.匀速圆周运动是匀速率圆周运动
D.在任意相等的时间内通过的路程相等
【分析】明确匀变速运动的性质,知道匀速圆周运动速度大小不变,方向变化,是变速运动.加速度方向始终指向圆心,加速度是变化的,是变加速运动。
【解答】解:A、匀速圆周运动是速度大小不变的圆周运动,故A错误;
B、匀速圆周运动所受合力提供向心力,故匀速圆周运动一定是变加速运动;
C、匀速圆周运动速度大小不变,故C正确;
D、由于速率不变,故D正确。
故选:CD。
三.解答题(共2小题)
18.如图所示,半径为0.1m的轻滑轮,通过绕在其上面的细线与重物相连2的加速度匀加速下落,则当它下落高度为1 m时的瞬时速度是多大?此刻的滑轮转动的角速度是多大?
【分析】由位移速度公式即可求出下落高度为1 m时的瞬时速度;根据线速度与角速度的关系即可求出角速度.
【解答】解:重物以加速度a=2m/s2做匀加速运动,由公式:
又因有:,
代入数据得:
答:下落高度为6 m时的瞬时速度是2m/s
19.如图是一行星绕恒星做匀速圆周运动的示意图,由天文观测可得其运行周期为T,速度为v,试求:
(1)行星运动的轨道半径R;
(2)行星运动的加速度a;
(3)恒星的质量M.
【分析】根据圆周运动知识和已知物理量求出轨道半径.
根据万有引力提供向心力,列出等式求出中心体的质量和加速度.
【解答】解:(1)因v=ωR=,所以R=;
(2)行星的加速度a=ωv=
(3)根据半径R,结合万有引力定律公式G=,
答:(1)行星运动的轨道半径R为;
(2)行星运动的加速度a为;
(3)恒星的质量M为
第1页(共1页)
一.选择题(共12小题)
1.如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,管道内侧壁半径为R,则下列说法中正确的是( )
A.小球通过最高点时的最小速度vmin=
B.小球通过最高点时的最小速度vmin=0 m/s
C.小球在水平线ab以下的管道中运动时,内侧管壁对小球一定有作用力
D.小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力
2.下列生活中的一些现象是利用到了离心运动的是( )
A.驾驶汽车时必须系安全带
B.汽车过凹形路面时必须减速
C.火车轨道外高内低
D.洗衣机的脱水桶
3.如图所示,长为L的细轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,这样就构成了一个圆锥摆.不计空气阻力,关于小球受力( )
A.小球只受重力和向心力作用
B.小球只受重力和绳的拉力作用
C.小球只受重力、绳的拉力和向心力作用
D.小球只受重力、绳的拉力和离心力作用
4.如图所示,一圆柱形容器绕其轴线匀速转动,内部有A、B两个物体(A、B与容器接触面间仍相对静止),下列说法正确的是( )
A.两物体受到的摩擦力都增大
B.两物体受到的摩擦力大小都不变
C.物体A受到的摩擦力增大,物体B受到的摩擦力大小不变
D.物体A受到的摩擦力大小不变,物体B受到的摩擦力增大
5.一精确转动的机械手表,秒针的角速度大约为( )
A.0.05rad/s B.0.1rad/s C.1rad/s D.6rad/s
6.下列说法中正确的是( )
A.变速运动不一定都是曲线运动,曲线运动一定都是变速运动
B.平抛运动的物体每秒内速度大小的增量相等
C.匀速圆周运动的物体线速度保持不变
D.圆周运动的物体加速度一定指向圆心
7.如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a和b是轮边缘上的两个点( )
A.角速度大小相同 B.线速度大小相同
C.周期大小不同 D.转速大小不同
8.如图所示,A、B两轮属于摩擦传动,两轮半径RA=2RB,P、Q为两轮边缘上的点,当主动轮A匀速转动时,P、Q两点角速度大小之比为( )
A.2:1 B.1:2 C.1:1 D.1:4
9.对于做匀速圆周运动的物体,下面说法中正确的是( )
A.速度在改变,动能也在改变
B.速度改变,动能不变
C.速度不变,动能改变
D.动能、速度都不变
10.如图所示,是中国古代玩具饮水鸟,它的神奇之处是,鸟就会俯下身去,把嘴浸到水里,鸟将绕着O点不停摆动,一会儿它又会俯下身去,OA>OB,则在摆动过程中( )
A.A、B两点的线速度大小相同
B.A、B两点的线速度方向相同
C.A、B两点的角速度大小相同
D.A、B两点的向心加速度大小相等
11.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc C.Fc<Fa<Fb D.Fa>Fc>Fb
12.暑假期间,某同学乘坐高铁外出旅游,他观察到高铁两旁的树木急速向后退行,他发现水平桌面上玻璃杯中的水面呈现左低右高的状态,如图所示( )
A.加速行驶 B.减速行驶 C.向右转弯 D.向左转弯
二.多选题(共5小题)
13.如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带不打滑( )
A.A、B、C三点的加速度之比aA:aB:aC=6:2:1
B.A、B、C三点的线速度大小之比vA:vB:vC=3:2:2
C.A、B、C三点的角速度之比ωA:ωB:ωC=2:2:1
D.A、B、C三点的周期之比TA:TB:TC=1:1:2
14.长为L的轻杆,一端固定一个小球,以另一端O为圆心,关于小球在最高点的速度v下列说法中正确的是( )
A.当v的值小于时,杆对小球的弹力指向圆心
B.当v由逐渐增大,杆对小球的拉力逐渐增大
C.当v由逐渐减小时,杆对小球的支持力逐渐减小
D.当v由零逐渐增大时,向心力也逐渐增大
15.一个小球以大小为a=4m/s2的向心加速度做匀速圆周运动,半径R=1m,则下列说法正确的是( )
A.小球运动的角速度为2rad/s
B.小球做圆周运动的周期为πs
C.小球在t=s内通过的位移大小为m
D.小球在πs内通过的路程为零
16.一圆周半径为R,质点沿着这个圆周运动,当它通过1,设此过程中的最大位移的大小为x,则以下说法正确的是( )
A.θ=90° B.θ=450° C.x=R D.x=2R
17.关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀速运动
B.匀速圆周运动是匀变速运动
C.匀速圆周运动是匀速率圆周运动
D.在任意相等的时间内通过的路程相等
三.解答题(共2小题)
18.如图所示,半径为0.1m的轻滑轮,通过绕在其上面的细线与重物相连2的加速度匀加速下落,则当它下落高度为1 m时的瞬时速度是多大?此刻的滑轮转动的角速度是多大?
19.如图是一行星绕恒星做匀速圆周运动的示意图,由天文观测可得其运行周期为T,速度为v,试求:
(1)行星运动的轨道半径R;
(2)行星运动的加速度a;
(3)恒星的质量M.
人教版(2019)必修第二册《第6章 圆周运动》2021年单元测试卷(4)
参考答案与试题解析
一.选择题(共12小题)
1.如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,管道内侧壁半径为R,则下列说法中正确的是( )
A.小球通过最高点时的最小速度vmin=
B.小球通过最高点时的最小速度vmin=0 m/s
C.小球在水平线ab以下的管道中运动时,内侧管壁对小球一定有作用力
D.小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力
【分析】小球在竖直光滑圆形管道内做圆周运动,在最高点,由于外管或内管都可以对小球产生弹力作用,从而可以确定在最高点的最小速度.小球做圆周运动时,沿半径方向的合力提供做圆周运动的向心力.
【解答】解:A、在最高点,当小球的速度等于0时,大小为mg.故A错误。
C、小球在水平线ab以下管道运动,所以外侧管壁对小球一定有作用力。故C错误。
D、小球在水平线ab以上管道运动,当速度较大时,此时外侧管壁有作用力,内侧管壁有作用力。
故选:B。
2.下列生活中的一些现象是利用到了离心运动的是( )
A.驾驶汽车时必须系安全带
B.汽车过凹形路面时必须减速
C.火车轨道外高内低
D.洗衣机的脱水桶
【分析】驾驶汽车时必须系安全带是为了避免惯性带来的伤害;汽车过凹形路面时必须减速是为了防止爆胎;火车轨道外高内低是防止与轨道挤压;洗衣机的脱水桶是利用了离心运动。
【解答】解:A、驾驶汽车时必须系安全带是为了避免惯性带来的伤害;
B、汽车过凹形路面时必须减速是为了防止爆胎;
C、火车轨道外高内低是防止与轨道挤压;
D、洗衣机的脱水桶是利用了离心运动。
故选:D。
3.如图所示,长为L的细轻绳一端固定,另一端系一质量为m的小球.给小球一个合适的初速度,这样就构成了一个圆锥摆.不计空气阻力,关于小球受力( )
A.小球只受重力和向心力作用
B.小球只受重力和绳的拉力作用
C.小球只受重力、绳的拉力和向心力作用
D.小球只受重力、绳的拉力和离心力作用
【分析】分析小球的受力,受到重力、绳的拉力,二者的合力提供向心力,向心力是效果力,不是重复受力.
【解答】解:小球做匀速圆周运动,合力不为零,提供向心力;
小球受重力和细线的拉力,共2个力,对惯性系没有离心力的说法;
故ACD错误,B正确;
故选:B。
4.如图所示,一圆柱形容器绕其轴线匀速转动,内部有A、B两个物体(A、B与容器接触面间仍相对静止),下列说法正确的是( )
A.两物体受到的摩擦力都增大
B.两物体受到的摩擦力大小都不变
C.物体A受到的摩擦力增大,物体B受到的摩擦力大小不变
D.物体A受到的摩擦力大小不变,物体B受到的摩擦力增大
【分析】分别对物体A、B受力分析,根据牛顿第二定律和共点力平衡即可判断摩擦力的变化。
【解答】解:对A分析,A在竖直方向受力平衡1=mg,故转速增大后摩擦力不变;
对B分析,B受到的摩擦力提供向心力2=m(6πn)2r,由于转速增大,故ABC错误;
故选:D。
5.一精确转动的机械手表,秒针的角速度大约为( )
A.0.05rad/s B.0.1rad/s C.1rad/s D.6rad/s
【分析】角速度是描述物体转动快慢的物理量,加速度ω==
【解答】解:秒针转动一圈的时间为60s,角速度ω==。
故选:B。
6.下列说法中正确的是( )
A.变速运动不一定都是曲线运动,曲线运动一定都是变速运动
B.平抛运动的物体每秒内速度大小的增量相等
C.匀速圆周运动的物体线速度保持不变
D.圆周运动的物体加速度一定指向圆心
【分析】曲线运动的速度方向时刻变化,为变速运动,但变速运动并不一定为曲线运动,可能为变速直线运动,平抛运动为加速度恒定的匀变速曲线运动,匀速圆周运动是速率不变的圆周运动,匀速圆周运动的向心加速度指向圆心,但变速圆周运动的加速度不指向圆心。
【解答】解:A、曲线运动的瞬时速度方向时刻发生改变,但变速运动有可能是变速直线运动;
B、平抛运动匀变速曲线运动,每秒内速度的增量△v=g△t=10m/s,但每秒内速度的大小增量不等;
C、匀速圆周运动线速度方向时刻发生改变,故C错误;
D、只有匀速圆周运动加速度指向圆心,故D错误
故选:A。
7.如图所示,一偏心轮绕垂直纸面的轴O匀速转动,a和b是轮边缘上的两个点( )
A.角速度大小相同 B.线速度大小相同
C.周期大小不同 D.转速大小不同
【分析】a、b两点共轴转动,角速度相等,则周期与转速相等,根据转动半径的大小比较线速度的大小即可.
【解答】解:A、D、a、b两点共轴转动,转速相等,D错误;
B、由于转动的半径不等,线速度大小不等;
C、根据T=,a,则周期一定相等。
故选:A。
8.如图所示,A、B两轮属于摩擦传动,两轮半径RA=2RB,P、Q为两轮边缘上的点,当主动轮A匀速转动时,P、Q两点角速度大小之比为( )
A.2:1 B.1:2 C.1:1 D.1:4
【分析】A和B靠摩擦传动,边缘上各点的线速度相同,根据线速度角速度关系可得出角速度的关系。
【解答】解:A、B两轮靠轮边缘间的摩擦转动,
由v=ωR可知:线速度相等时,角速度与半径成反比
ωA:ωB=RB:RA=1:2,即P,故B正确。
故选:B。
9.对于做匀速圆周运动的物体,下面说法中正确的是( )
A.速度在改变,动能也在改变
B.速度改变,动能不变
C.速度不变,动能改变
D.动能、速度都不变
【分析】速度是矢量,有大小有方向,要保持不变,大小和方向都不变.在匀速圆周运动的过程中,速度的方向时刻改变,所以速度变化,动能是标量,不发生改变.
【解答】解:匀速圆周运动的过程中,线速度的大小不变,所以线速度改变,不发生改变。
故选:B。
10.如图所示,是中国古代玩具饮水鸟,它的神奇之处是,鸟就会俯下身去,把嘴浸到水里,鸟将绕着O点不停摆动,一会儿它又会俯下身去,OA>OB,则在摆动过程中( )
A.A、B两点的线速度大小相同
B.A、B两点的线速度方向相同
C.A、B两点的角速度大小相同
D.A、B两点的向心加速度大小相等
【分析】A、B两点属于同轴转动的模型,同轴转动角速度相等,根据v=ωr,a=ω2r分析线速度和加速度。
【解答】解:C、根据同轴转动角速度相等知,A,故C正确。
AB、根据v=ωr知A点半径大,线速度方向就是该点的运动方向,故AB错误。
D、根据a=ω2r知A点半径大,加速度较大。
故选:C。
11.如图所示,一辆电动车在水平地面上以恒定速率v行驶,依次通过a,b,比较三个点向心力大小( )
A.Fa>Fb>Fc B.Fa<Fb<Fc C.Fc<Fa<Fb D.Fa>Fc>Fb
【分析】由图象知轨道半径大小关系,根据向心力公式F=m比较向心力的大小。
【解答】解:根据向心力公式F=m知v大小相等,向心力越小a>rb>rc,所以Fa<Fb<Fc,故B正确,ACD错误。
故选:B。
12.暑假期间,某同学乘坐高铁外出旅游,他观察到高铁两旁的树木急速向后退行,他发现水平桌面上玻璃杯中的水面呈现左低右高的状态,如图所示( )
A.加速行驶 B.减速行驶 C.向右转弯 D.向左转弯
【分析】水面上有一个质量为m的水滴,分析该水滴受到的合外力方向,由此进行判断。
【解答】解:设水面上有一个质量为m的水滴,受到重力和周围水对它的作用力
说明该水滴受到的合外力方向向左,相对于该同学来说,故D正确。
故选:D。
二.多选题(共5小题)
13.如图所示的皮带传动装置,主动轮O1上两轮的半径分别为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带不打滑( )
A.A、B、C三点的加速度之比aA:aB:aC=6:2:1
B.A、B、C三点的线速度大小之比vA:vB:vC=3:2:2
C.A、B、C三点的角速度之比ωA:ωB:ωC=2:2:1
D.A、B、C三点的周期之比TA:TB:TC=1:1:2
【分析】靠传送带传动的两个轮子边缘上各点的线速度大小相等,共轴转动的各点,角速度相等。B点和C点具有相同的线速度,A点和B点具有相同的角速度。根据v=rω,求出三点的角速度之比和线速度之比。根据a=ωv求解加速度之比,根据T=求解周期之比。
【解答】解:C、B点和C点具有相同大小的线速度,知B,所以ωB:ωC=rC:rB=2:1.而A点和B点具有相同的角速度A:ωB:ωC=6:2:1.故C正确;
B、根据v=rω,所以vA:vB:=5:1.BC线速度相等A:vB:vC=3:8:1.故B错误
A、根据a=vω得:aA:aB:aC=vAωA:aB:vBωB:vCωC=6:3:1.故A正确;
D、根据T=A:TB:TC==6:1:2。
故选:ACD。
14.长为L的轻杆,一端固定一个小球,以另一端O为圆心,关于小球在最高点的速度v下列说法中正确的是( )
A.当v的值小于时,杆对小球的弹力指向圆心
B.当v由逐渐增大,杆对小球的拉力逐渐增大
C.当v由逐渐减小时,杆对小球的支持力逐渐减小
D.当v由零逐渐增大时,向心力也逐渐增大
【分析】当速度v=,小球靠重力提供向心力,杆子的作用力为零;若,杆子表现为支持力,若v,杆子表现为拉力,结合牛顿第二定律分析判断.
【解答】解:A、在最高点,小球靠重力提供向心力,若v,即杆对小球的弹力方向背离圆心。
B、当v由,杆子表现为拉力,速度增大,故B正确。
C、当v由,杆子表现为支持力,速度减小,故C错误。
D、根据知,向心力增大。
故选:BD。
15.一个小球以大小为a=4m/s2的向心加速度做匀速圆周运动,半径R=1m,则下列说法正确的是( )
A.小球运动的角速度为2rad/s
B.小球做圆周运动的周期为πs
C.小球在t=s内通过的位移大小为m
D.小球在πs内通过的路程为零
【分析】依据a=ω2r可得角速度,根据求周期,根据V=ωr求线速度,根据l=vt求路程.
【解答】解:A、ω==,故A正确;
B、周期T=,故B正确;
C、根据V=ωr,t==m,故C错误;
D、小球在πs内通过的路程为l=vt=2×π=2π;
故选:AB。
16.一圆周半径为R,质点沿着这个圆周运动,当它通过1,设此过程中的最大位移的大小为x,则以下说法正确的是( )
A.θ=90° B.θ=450° C.x=R D.x=2R
【分析】根据圆周运动的规律可明确转过的角度,再根据位移的定义由几何关系即可求出最大位移.
【解答】解:A、做圆周运动的物体每转动一周,故通过1=450°,B正确;
C、此时物体从起点又转动了周R;故C正确;
故选:BC。
17.关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀速运动
B.匀速圆周运动是匀变速运动
C.匀速圆周运动是匀速率圆周运动
D.在任意相等的时间内通过的路程相等
【分析】明确匀变速运动的性质,知道匀速圆周运动速度大小不变,方向变化,是变速运动.加速度方向始终指向圆心,加速度是变化的,是变加速运动。
【解答】解:A、匀速圆周运动是速度大小不变的圆周运动,故A错误;
B、匀速圆周运动所受合力提供向心力,故匀速圆周运动一定是变加速运动;
C、匀速圆周运动速度大小不变,故C正确;
D、由于速率不变,故D正确。
故选:CD。
三.解答题(共2小题)
18.如图所示,半径为0.1m的轻滑轮,通过绕在其上面的细线与重物相连2的加速度匀加速下落,则当它下落高度为1 m时的瞬时速度是多大?此刻的滑轮转动的角速度是多大?
【分析】由位移速度公式即可求出下落高度为1 m时的瞬时速度;根据线速度与角速度的关系即可求出角速度.
【解答】解:重物以加速度a=2m/s2做匀加速运动,由公式:
又因有:,
代入数据得:
答:下落高度为6 m时的瞬时速度是2m/s
19.如图是一行星绕恒星做匀速圆周运动的示意图,由天文观测可得其运行周期为T,速度为v,试求:
(1)行星运动的轨道半径R;
(2)行星运动的加速度a;
(3)恒星的质量M.
【分析】根据圆周运动知识和已知物理量求出轨道半径.
根据万有引力提供向心力,列出等式求出中心体的质量和加速度.
【解答】解:(1)因v=ωR=,所以R=;
(2)行星的加速度a=ωv=
(3)根据半径R,结合万有引力定律公式G=,
答:(1)行星运动的轨道半径R为;
(2)行星运动的加速度a为;
(3)恒星的质量M为
第1页(共1页)
