华东师大版七上数学 4.6.2角的比较和运算 课件(共24张)
文档属性
| 名称 | 华东师大版七上数学 4.6.2角的比较和运算 课件(共24张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 642.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 00:39:21 | ||
图片预览




文档简介
(共24张PPT)
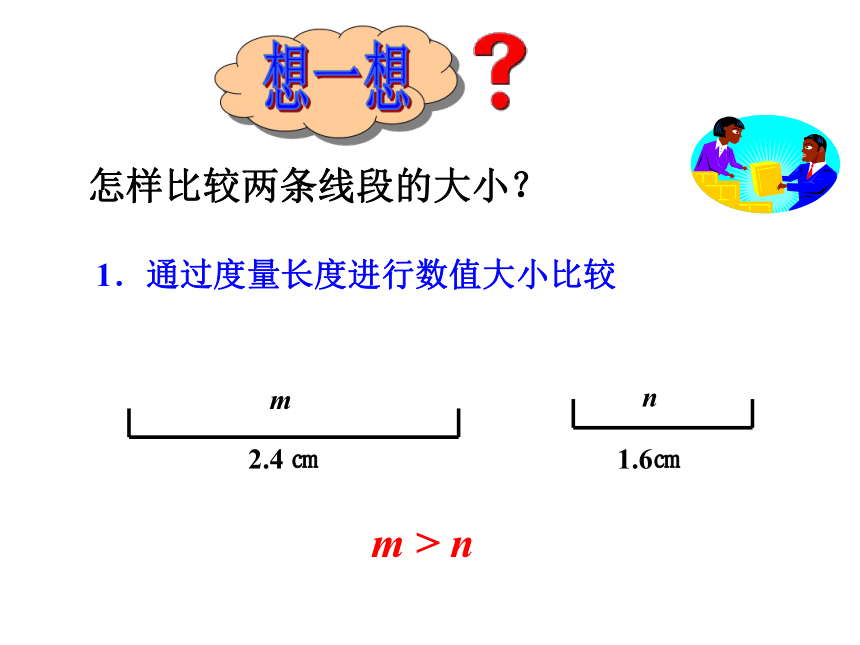
1.通过度量长度进行数值大小比较
2.4 ㎝
1.6㎝
m
n
m > n
怎样比较两条线段的大小?
A
B
A
C
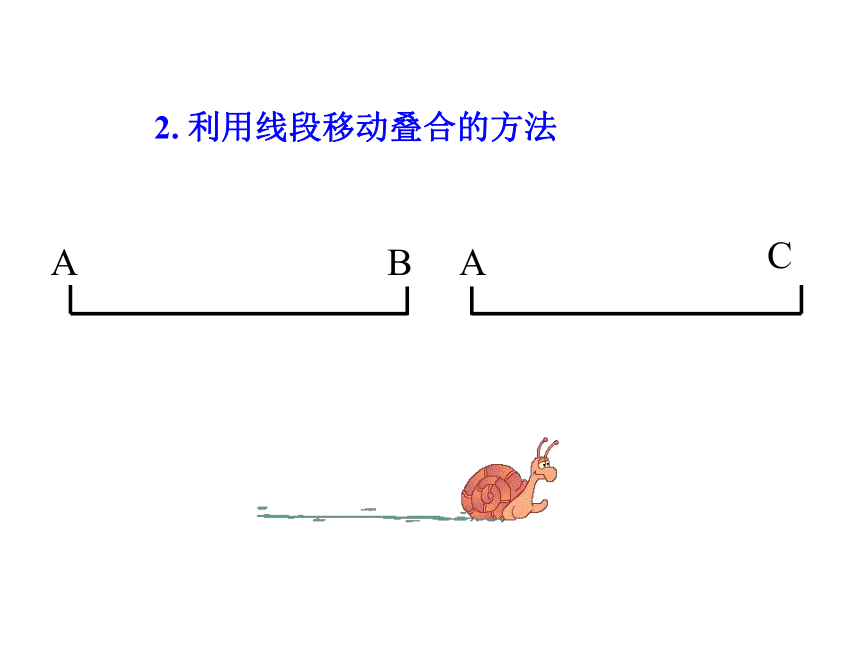
2. 利用线段移动叠合的方法
A
( C )
A
C
A
B
C
A
A
B
A
B
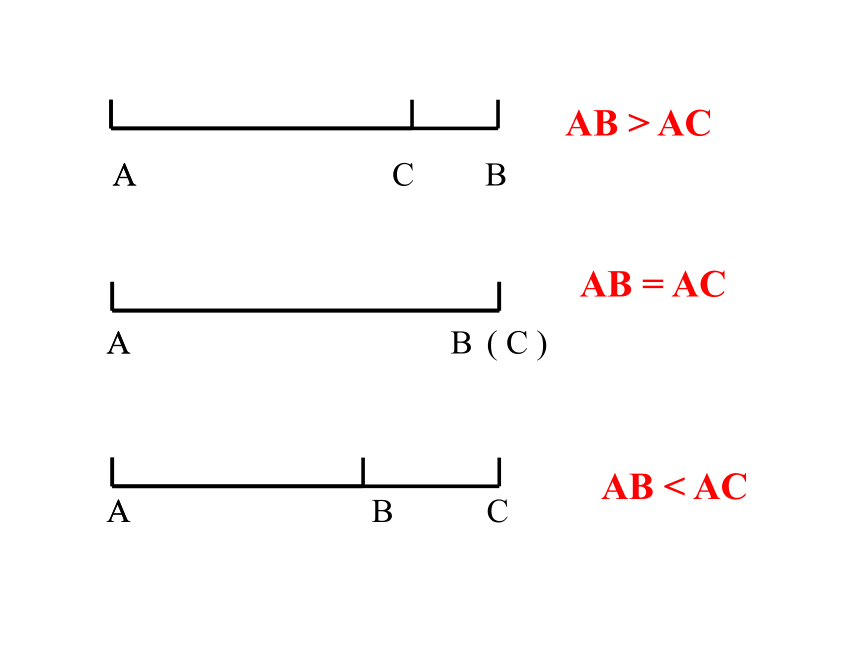
AB > AC
AB = AC
AB < AC
这两把折扇中,哪一把形成的角度大?与折扇的大小有关系吗?
新课导入
判断:下图中∠1>∠2吗?
角的大小与角的边长无关!
1
2
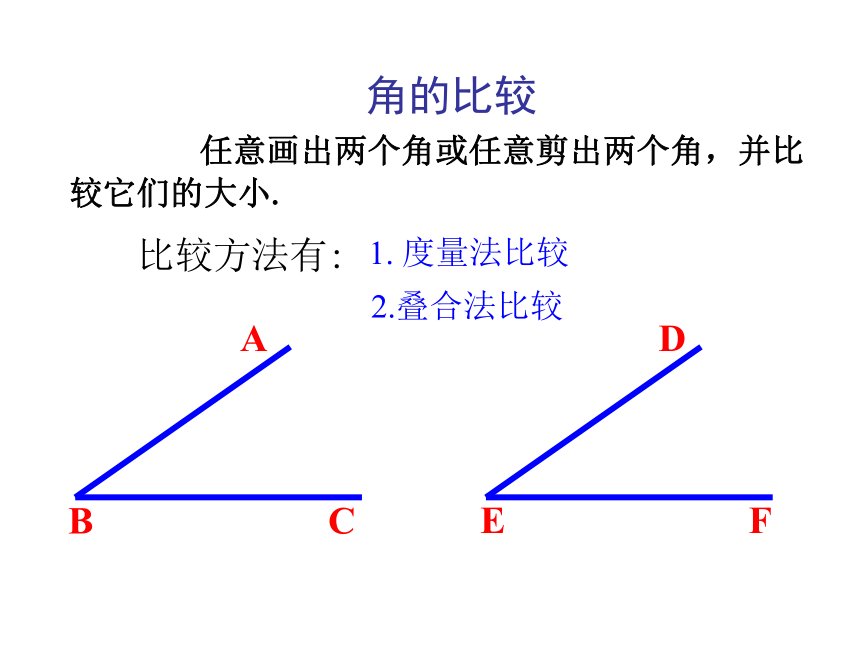
任意画出两个角或任意剪出两个角,并比较它们的大小.
B
A
C
E
D
F
比较方法有:
1. 度量法比较
2.叠合法比较
角的比较
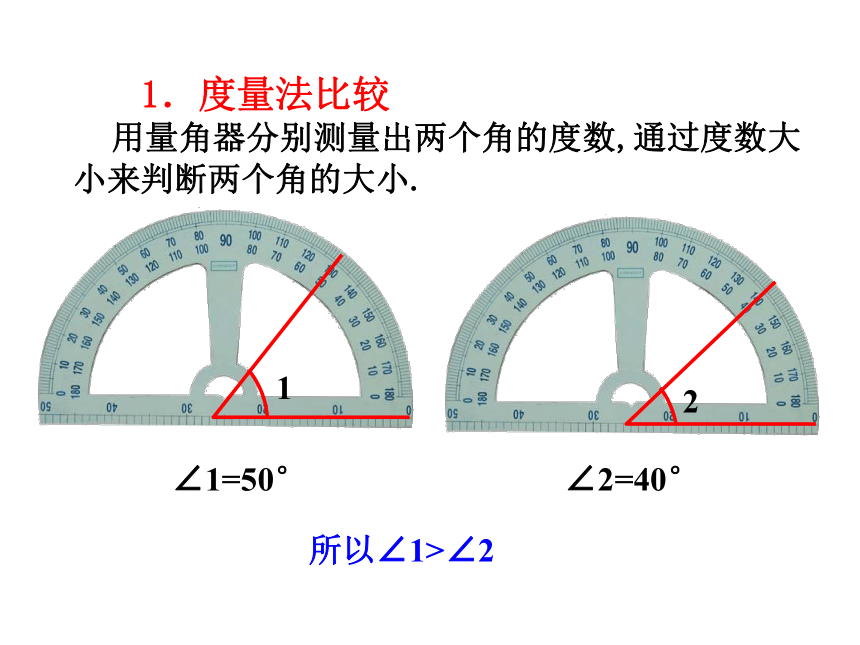
1.度量法比较
∠1=50°
∠2=40°
所以∠1>∠2
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
1
2
2.叠合法比较
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
1. 如果EC与OD重合,那么∠AEC等于
∠BOD,记作∠AEC=∠BOD.
E
A
C
O
B
D
2.如果EC落在∠BOD的内部,那么∠AEC小
于∠BOD,记作∠AEC<∠BOD.
E
A
C
O
B
D
3.如果EC落在∠BOD的外部,那∠AEC
大于∠BOD,记作∠AEC>∠BOD.
O
B
D
E
A
C
你能总结出两个角的大小关系有几种吗?
问题1
图中共有几个角?它们之间有什么关系?
答:有三个角,关系是:
∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC,
∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC,
角的运算
D
O
C
B
A
(1)∠AOD=_______+________+__________;
(2) ∠BOC=________-___________=_________-________;
(3) ∠AOB____∠AOC;(填>或<)
∠AOB
∠BOC
∠COD
∠AOC
∠AOB
∠BOD
∠COD
<
练一练
1. 请观察右图
并完成下列问题
2.如图,O是直线MN上一点,∠NOP=153°48′30″,求∠MOP的度数.
解:依题意可知:∠MON是平角.
因为∠MON=∠MOP+∠NOP,
所以∠MOP=∠MON-∠NOP
=180°- 163°48′30″
=16°11′30″.
答: ∠MOP的度数为16°11′30″.
度、分、秒相减时,要借1作60.
N
O
M
P
问题2
利用一副三角板,你能画出哪些度数的角?这些角有什么规律?
观察思考,探究新知
请拿出我们上节课所做的角,将这个角对折,使其两边重合,折痕与角两边所成的两个角的大小有什么关系?
相等.
观察思考,探究新知
问题3
如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2 ,
∠AOB=∠BOC= .
∠AOC
∠BOC
我们把射线OB叫做∠AOC的角平分线.
类比线段中点的定义,你能给角平分线下定义吗?
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
角平分线的定义
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线.
1. 如图,AD是∠BAC的平分线,找出图中相等的角.
A
B
C
D
练一练
∠BAD=∠CAD
A
O
B
M
2.如上图若∠AOM=∠BOM,
那么∠AOB=2__________=2___________,
∠AOM=∠BOM= ____________.
∠AOM
∠BOM
∠AOB
OM是∠AOB的角平分线.
如图, ∠AOB是已知角,用圆规和直尺画一个角等于∠AOB.
A
O
B
D′
C′
C
D
B′
O′
A′
1.角的比较方法
(1)度量法;
(2)叠合法.
2.角的和与差
3.角平分线的定义
课堂小结
随堂练习
让我们来场小比赛看哪组完成 学案最快,最准确!
1.通过度量长度进行数值大小比较
2.4 ㎝
1.6㎝
m
n
m > n
怎样比较两条线段的大小?
A
B
A
C
2. 利用线段移动叠合的方法
A
( C )
A
C
A
B
C
A
A
B
A
B
AB > AC
AB = AC
AB < AC
这两把折扇中,哪一把形成的角度大?与折扇的大小有关系吗?
新课导入
判断:下图中∠1>∠2吗?
角的大小与角的边长无关!
1
2
任意画出两个角或任意剪出两个角,并比较它们的大小.
B
A
C
E
D
F
比较方法有:
1. 度量法比较
2.叠合法比较
角的比较
1.度量法比较
∠1=50°
∠2=40°
所以∠1>∠2
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
1
2
2.叠合法比较
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
1. 如果EC与OD重合,那么∠AEC等于
∠BOD,记作∠AEC=∠BOD.
E
A
C
O
B
D
2.如果EC落在∠BOD的内部,那么∠AEC小
于∠BOD,记作∠AEC<∠BOD.
E
A
C
O
B
D
3.如果EC落在∠BOD的外部,那∠AEC
大于∠BOD,记作∠AEC>∠BOD.
O
B
D
E
A
C
你能总结出两个角的大小关系有几种吗?
问题1
图中共有几个角?它们之间有什么关系?
答:有三个角,关系是:
∠BOC是 ∠AOC与 ∠AOB的差,记作 ∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与 ∠BOC的和,记作 ∠AOC=∠AOB+∠BOC,
∠AOB是 ∠AOC与 ∠BOC的差,记作 ∠AOB=∠AOC-∠BOC,
角的运算
D
O
C
B
A
(1)∠AOD=_______+________+__________;
(2) ∠BOC=________-___________=_________-________;
(3) ∠AOB____∠AOC;(填>或<)
∠AOB
∠BOC
∠COD
∠AOC
∠AOB
∠BOD
∠COD
<
练一练
1. 请观察右图
并完成下列问题
2.如图,O是直线MN上一点,∠NOP=153°48′30″,求∠MOP的度数.
解:依题意可知:∠MON是平角.
因为∠MON=∠MOP+∠NOP,
所以∠MOP=∠MON-∠NOP
=180°- 163°48′30″
=16°11′30″.
答: ∠MOP的度数为16°11′30″.
度、分、秒相减时,要借1作60.
N
O
M
P
问题2
利用一副三角板,你能画出哪些度数的角?这些角有什么规律?
观察思考,探究新知
请拿出我们上节课所做的角,将这个角对折,使其两边重合,折痕与角两边所成的两个角的大小有什么关系?
相等.
观察思考,探究新知
问题3
如图,如果∠AOB=∠BOC,那么
∠AOC=2∠AOB=2 ,
∠AOB=∠BOC= .
∠AOC
∠BOC
我们把射线OB叫做∠AOC的角平分线.
类比线段中点的定义,你能给角平分线下定义吗?
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
角平分线的定义
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线.
1. 如图,AD是∠BAC的平分线,找出图中相等的角.
A
B
C
D
练一练
∠BAD=∠CAD
A
O
B
M
2.如上图若∠AOM=∠BOM,
那么∠AOB=2__________=2___________,
∠AOM=∠BOM= ____________.
∠AOM
∠BOM
∠AOB
OM是∠AOB的角平分线.
如图, ∠AOB是已知角,用圆规和直尺画一个角等于∠AOB.
A
O
B
D′
C′
C
D
B′
O′
A′
1.角的比较方法
(1)度量法;
(2)叠合法.
2.角的和与差
3.角平分线的定义
课堂小结
随堂练习
让我们来场小比赛看哪组完成 学案最快,最准确!
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
