2021-2022学年 沪教新版九年级上册数学 期中考试复习试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年 沪教新版九年级上册数学 期中考试复习试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 449.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 06:46:56 | ||
图片预览



文档简介
2021-2022学年沪教新版九年级上册数学期中复习试卷
一.选择题(共6小题,满分24分,每小题4分)
1.下列函数中,属于二次函数的是( )
A.y=x2﹣(x+4)(x+2) B.y=2(x+1)(x﹣3)
C.y=ax2+bx+c D.y=
2.在△ABC和△DEF中,AB=3DE,AC=3DF,∠A=∠D.如果△ABC的周长为24,面积为18,则△DEF的周长、面积分别是( )
A.8,6 B.8,2 C.,6 D.,2
3.已知二次函数y=x2﹣6x+8,当0<x≤m时,﹣1≤y≤8,则m的值是( )
A.3 B.4 C.6 D.7
4.若2a=3b(a≠0),则的值为( )
A. B. C.2 D.3
5.下列命题中,是真命题的是( )
A.等腰三角形都相似 B.等边三角形都相似
C.锐角三角形都相似 D.直角三角形都相似
6.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(1)abc>0;(2)b<a+c;(3)4a+2b+c>0;(4)2c<3b;(5)a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共12小题,满分48分,每小题4分)
7.在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为 米.
8.如果抛物线y=ax2﹣1的顶点是它的最低点,那么a的取值范围是 .
9.抛物线y=x2﹣2x+3的对称轴是 .
10.若函数y=a(x﹣h)2+k(a≠0)的图象经过原点,最大值为16,且形状与抛物线y=﹣4x2+2x﹣3相同,则此函数的关系式为 .
11.已知二次函数y=﹣x2+2x+5,若P(n,y1),Q(n﹣2,y2)是该二次函数图象上的两点,且y1>y2,则实数n的取值范围为 .
12.化简:= .
13.已知一个直角三角形的两条直角边长分别为3和6,则该三角形的重心到其直角顶点的距离是 .
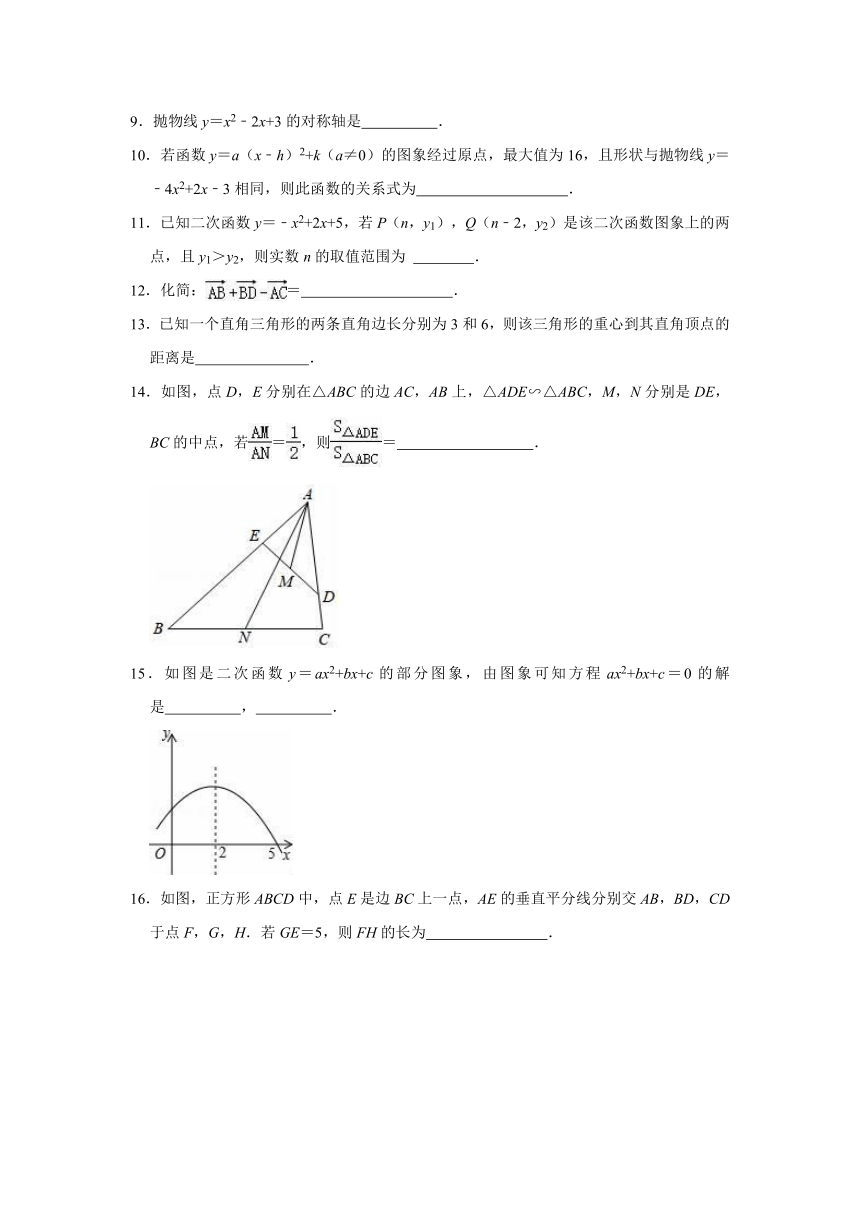
14.如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若=,则= .
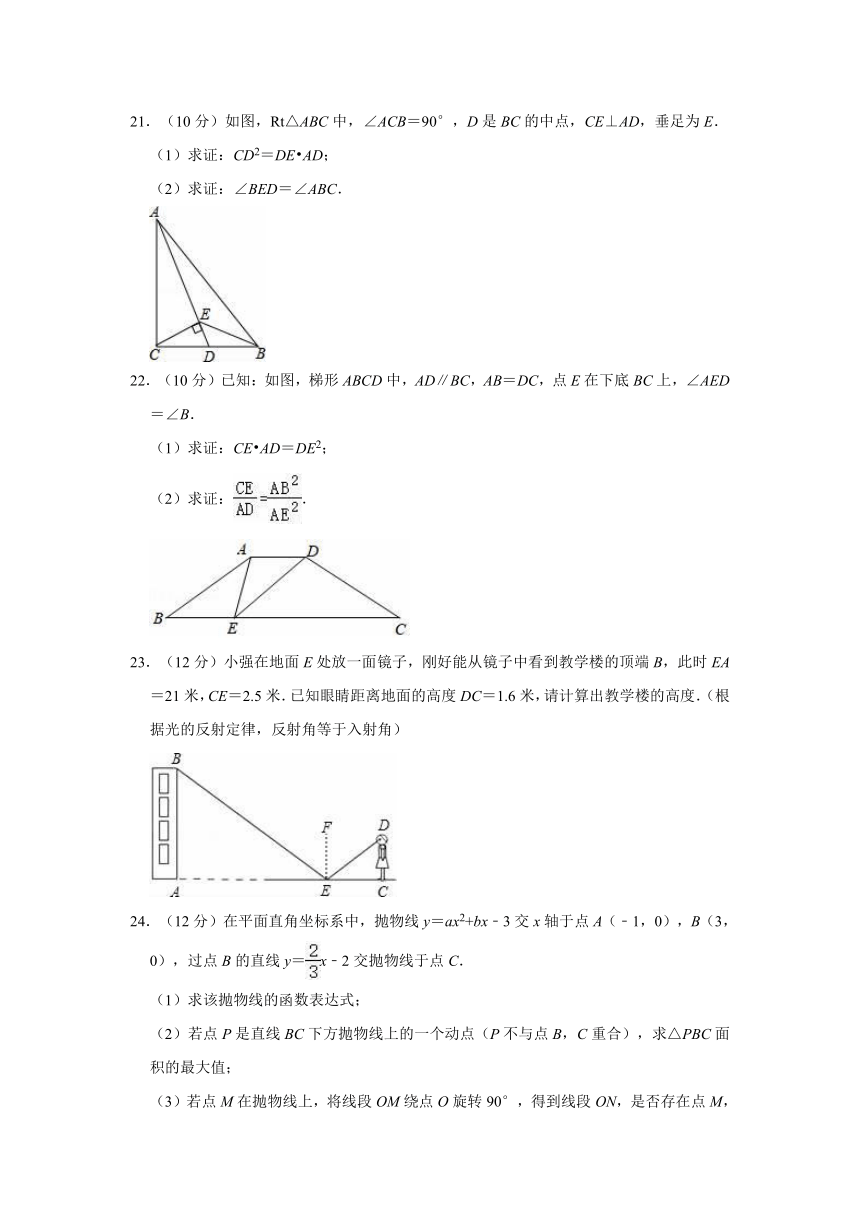
15.如图是二次函数y=ax2+bx+c的部分图象,由图象可知方程ax2+bx+c=0的解是 , .
16.如图,正方形ABCD中,点E是边BC上一点,AE的垂直平分线分别交AB,BD,CD于点F,G,H.若GE=5,则FH的长为 .
17.如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,D为AB边上一动点,连接CD,△ACD与△A′CD关于直线CD轴对称,连接BA′,则BA′的最小值为 .
18.如图,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°,= .
三.解答题(共7小题,满分78分)
19.(10分)已知==,求的值.
20.(10分)如图,已知二次函数y=ax2+bx+c的图象过点A(﹣1,0)和点C(0,3),对称轴为直线x=1.
(1)求该二次函数的关系式和顶点坐标;
(2)结合图象,当y<3时,直接写出x的取值范围.
21.(10分)如图,Rt△ABC中,∠ACB=90°,D是BC的中点,CE⊥AD,垂足为E.
(1)求证:CD2=DE AD;
(2)求证:∠BED=∠ABC.
22.(10分)已知:如图,梯形ABCD中,AD∥BC,AB=DC,点E在下底BC上,∠AED=∠B.
(1)求证:CE AD=DE2;
(2)求证:.
23.(12分)小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
24.(12分)在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0),B(3,0),过点B的直线y=x﹣2交抛物线于点C.
(1)求该抛物线的函数表达式;
(2)若点P是直线BC下方抛物线上的一个动点(P不与点B,C重合),求△PBC面积的最大值;
(3)若点M在抛物线上,将线段OM绕点O旋转90°,得到线段ON,是否存在点M,使点N恰好落在直线BC上?若存在,请直接写出点M的坐标;若不存在,请说明理由.
25.(14分)如图1,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.EC与BD相交于点G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AD=2,求tan∠E;
(3)如图2,连接AG,请在下面选择EG,DG,AG三者之间的数量关系并证明.我的选择是 .
①EG﹣DG=AG;②EG﹣DG=AG;③EG﹣DG=AG.
参考答案与试题解析
一.选择题(共6小题,满分24分,每小题4分)
1.解:A、y=x2﹣(x+4)(x+2)=x2﹣x2﹣6x﹣8=﹣6x﹣8,是一次函数,故本选项不合题意;
B、y=2(x+1)(x﹣3)=2(x2﹣2x﹣3)=2x2﹣4x﹣6,是二次函数,故本选项符合题意;
C、y=ax2+bx+c,不一定是二次函数,故本选项不合题意;
D、y=的右边是分式,不是二次函数,故本选项不合题意;
故选:B.
2.解:在△ABC和△DEF中,
∵AB=3DE,
∴=3,
∵AC=3DF,
∴=3,
∴=,
∵∠A=∠D,
∴△ABC∽△DEF,
∴==3,
∵△ABC的周长为24,
∴△DEF的周长=×24=8,
∴==32=9
∵S△ABC=18,
∴S△DEF=S△ABC=2.
故选:B.
3.解:∵二次函数y=x2﹣6x+8=(x﹣3)2﹣1,
∴该函数的对称轴是直线x=3,函数图象开口向上,当x=3时取得最小值﹣1,
∵当0<x≤m时,﹣1≤y≤8,当x=0时,y=8,当x=6时,y=8,
∴m=6,
故选:C.
4.解:∵2a=3b(a≠0),
∴a=b,
∴==2;
故选:C.
5.解:A、等腰三角形不一定相似,是假命题,故A选项错误;
B、等边三角形都相似,是真命题,故B选项正确;
C、锐角三角形不一定都相似,是假命题,故C选项错误;
D、直角三角形不一定都相似,是假命题,故D选项错误.
故选:B.
6.解:(1)图象开口向下,与y轴交于正半轴,对称轴为x=1,能得到:a<0,c>0,﹣=1,
∴b=﹣2a>0,
∴abc<0,此结论错误;
②当x=﹣1时,由图象知y<0,
把x=﹣1代入解析式得:a﹣b+c<0,
∴b>a+c,
∴此结论错误;
③图象开口向下,与y轴交于正半轴,对称轴为x=1,
能得到:a<0,c>0,﹣=1,
所以b=﹣2a,
所以4a+2b+c=4a﹣4a+c>0,
∴此结论正确;
④∵由①②知b=﹣2a且b>a+c,
∴2c<3b,此结论正确;
⑤当x=1时,y=a+b+c,
当x=m时,y=am2+bm+c,
∵m≠1的实数,图象开口向下,对称轴为x=1,
∴a+b+c>am2+bm+c,
∴a+b>m(am+b),
∴此结论正确.
故选:B.
二.填空题(共12小题,满分48分,每小题4分)
7.解:设A,B两地的实际距离为xcm,则:
1:2000=4.5:x,
解得x=9000.
9000cm=90m.
故答案为:90.
8.解:∵抛物线y=ax2﹣1的顶点是它的最低点,
∴抛物线的开口向上,
∴a>0,
故答案为a>0.
9.解:对称轴为直线,
∵a=1,b=﹣2,
∴对称轴为直线.
故答案为:直线x=1.
10.解:∵函数y=a(x﹣h)2+k的图象经过原点,
把(0,0)代入解析式,得:ah2+k=0,
∵最大值为16,即函数的开口向下,a<0,顶点的纵坐标k=16,
又∵形状与抛物线y=﹣4x2+2x﹣3相同,
∴二次项系数a=﹣4,
把a=﹣4,k=16代入y=a(x﹣h)2+k中,得h=±2,
∴函数解析式是:y=﹣4(x﹣2)2+16或y=﹣4(x+2)2+16,
即y=﹣4x2﹣16x或y=﹣4x2+16x,
故答案为:y=﹣4x2﹣16x或y=﹣4x2+16x.
11.解:∵P(n,y1),Q(n﹣2,y2)是函数y=﹣x2+2x+5的图象上的两点,且y1>y2,
∴﹣n2+2n+5>﹣(n﹣2)2+2(n﹣2)+5,
化简整理得,4n﹣8<0,
∴n<2,
∴实数n的取值范围为n<2.
故答案为:n<2.
12.解:∵=﹣=+=.
故答案为.
13.解:∵直角三角形的两条直角边长分别为3和6,
∴斜边的长度为=3,
∴该三角形的重心到其直角顶点的距离是××3=,
故答案为:.
14.解:∵M,N分别是DE,BC的中点,
∴AM、AN分别为△ADE、△ABC的中线,
∵△ADE∽△ABC,
∴==,
∴=()2=,
故答案为:.
15.解:由图象可知对称轴x=2,与x轴的一个交点横坐标是5,它到直线x=2的距离是3个单位长度,所以另外一个交点横坐标是﹣1.
所以x1=﹣1,x2=5.
故答案是:x1=﹣1,x2=5.
16.解:过点H作HM⊥AB,垂足为M,设FH交AE于N,连接AG,CG,如图
∵FH是AE的垂直平分线,
∴∠ANF=90°,AN=NE,AG=GE,
∴∠BAE+∠AFN=90°,
∵四边形ABCD是正方形,
∴∠ABC=∠ADC=∠BAD=90°,AB=AD=BC,
∴∠BAE+∠AEB=90°,
∴∠AFN=∠AEB,
∵HM⊥AB,
∴∠AMH=∠HMF=90°,
∴四边形ADHM是矩形,
∴AD=HM=AB,
在△ABE和△HMF中,
,
∴△ABE≌△HMF(AAS),
∴FH=AE,
∵G在AE的垂直平分线HF上,
∴GA=GE=5,
∵BD是正方形ABCD的对角线,
∴∠ABG=∠CBG=45°,
在△ABG和△CBG中,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,∠GAB=∠GCB,
∴GE=GC,
∴∠GEC=∠GCE,
∴∠GEC=∠GAB,
∵∠GEC+∠GEB=180°,
∴∠GAB+∠GEB=180°,
∴∠AGE=360°﹣∠ABE﹣(∠BAG+∠GEB)=360°﹣90°﹣180°=90°,
∵GA=GE=5,
在Rt△AGE中,AE==5,
∴FH=AE=5,
故答案为:5.
17.解:∵∠ACB=90°,AC=3,AB=5,
∴BC==4,
∵△ACD与△A′CD关于直线CD轴对称,
∴CA′=CA=3,
∵BA′≥BC﹣BA(当且仅当B、A′、C共线时取等号),
∴BA′的最小值为4﹣3=1.
故答案为1.
18.解:过点A作AE⊥BC于E,过点D作DF⊥BC于F,
由(1)可知,EF=AE+DF,
∵∠B=∠C=45°,AE⊥BC,DF⊥BC,
∴∠B=∠BAE=45°,∠C=∠CDF=45°,
∴BE=AE,CF=DF,AB=AE,CD=DF,
∴BC=BE+EF+CF=2(AE+DF),
∴==.
故答案为:.
三.解答题(共7小题,满分78分)
19.解:设===k(k≠0),
∴x=2k,y=3k,z=4k,
∴==.
20.解:(1)根据题意得,
解得,.
∴二次函数的关系式为:y=﹣x2+2x+3,
∵y=﹣(x﹣1)2+4,
∴二次函数的顶点坐标(1,4).
(2)当y=3时,3=﹣(x﹣1)2+4,
解得,x1=0或x2=2,
∵y<3,
∴x<0或x>2.
21.证明(1)∵CE⊥AD,
∴∠CED=∠ACB=90°,
∵∠CDE=∠ADC,
∴△CDE∽△ADC,
∴CD:AD=DE:CD,
∴CD2=DE AD.
(2)∵D是BC的中点,
∴BD=CD;
∵CD2=DE AD,
∴BD2=DE AD
∴BD:AD=DE:BD;
又∵∠ADB=∠BDE,
∴△BDE∽△ADB,
∴∠BED=∠ABC.
22.证明:(1)∵梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠C,AB=DC,∠ADE=∠DEC,
∵∠AED=∠B,
∴∠C=∠AED,
∴△ADE∽△DEC,
∴,
∴CE AD=DE2;
(2)∵△ADE∽△DEC,
∴=,
∴=,
∴.
23.解:根据题意得∠AEB=∠CED,
∵Rt△AEB∽Rt△CED,
∴=,即=,
解得:AB=13.44.
答:教学楼的高度为13.44m.
24.解:(1)将点A(﹣1,0),B(3,0)代入y=ax2+bx﹣3 中,得:
,
解得:,
∴该抛物线表达式为y=x2﹣2x﹣3.
(2)如图1,过点P作PD∥y轴,交x轴于点D,交BC于点E,作CF⊥PD于点F,连接PB,PC,
设点P(m,m2﹣2m﹣3),则点E (m,),
∴PE=PD﹣DE=﹣m2+2m+3﹣(﹣m+2)=﹣m2+m+1,
联立方程组:,
解得:,,
∵点B坐标为(3,0),
∴点C的坐标为(,﹣),
∴BD+CF=3+,
∴S△PBC=S△PEB+S△PEC
=PE BD+PE CF
=PE(BD+CF)
=(﹣m2+m+1)
=()2+,(其中<m<3),
∵,
∴这个二次函数有最大值.
当m=时,S△PBC的最大值为.
(3)如图2,设M(t,t2﹣2t﹣3),N(n, n﹣2),
作MG⊥y轴于点G,NH⊥x轴于H,
∴∠OGM=∠OHN=90°,
∵线段OM绕点O旋转90°,得到线段ON,
∴OM=ON,∠MON=90°,
∵∠GOH=90°,
∴∠MOG=∠NOH,
在△OGM与△OHN中,
,
∴△OGM≌△OHN(AAS),
∴GM=NH,OG=OH,
∴,
解得:,,
M1(0,﹣3),M2,
如图3,设M(t,t2﹣2t﹣3),N(n, n﹣2),
作MG⊥x轴于点G,NH⊥x轴于H,
∴∠OGM=∠OHN=90°,
∵线段OM绕点O旋转90°,得到线段ON,
∴OM=ON,∠MON=90°,
∵∠GOH=90°,
∴∠MOG=∠NOH,
在△OGM与△OHN中,
,
∴△OGM≌△OHN(AAS),
∴GM=NH,OG=OH,
∴,
解得:t1=,t2=,
∴M3,M4(,);
综上所述,点M的坐标为M1(0,﹣3),M2,M3,M4(,).
25.(1)证明:∵四边形ABCD是矩形,点E在BA的延长线上,
∴∠EAF=∠DAB=90°,
又∵AE=AD,AF=AB,
∴△AEF≌△ADB(SAS),
∴∠AEF=∠ADB,
∴∠GEB+∠GBE=∠ADB+∠ABD=90°,
即∠EGB=90°,
∴BD⊥EC;
(2)解:∵AD=2,
∴AE=AD=2,
∵四边形ABCD是矩形,
∴AE∥CD,
∴∠AEF=∠DCF,∠EAF=∠CDF,
∴△AEF∽△DCF,
∴=,
∴AE DF=AF DC,
设AF=AB=a(a>0),则2(2﹣a)=a2,
整理得:a2+2a﹣4=0,
解得:a=﹣1+或﹣1﹣(舍去),
∴AF=﹣1+,
∴tanE==;
(3)解:我的选择是:②EG﹣DG=AG,证明如下:
在线段EG上取点P,使得EP=DG,连接AP,如图2所示:
∵AE=AD,∠AEP=∠ADG,EP=DG,
∴△AEP≌△ADG(SAS),
∴AP=AG,∠EAP=∠DAG,
∴∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,
∴△PAG为等腰直角三角形,
∴PG=AG,
∴EG﹣DG=EG﹣EP=PG=AG,
故答案为:②EG﹣DG=AG.
一.选择题(共6小题,满分24分,每小题4分)
1.下列函数中,属于二次函数的是( )
A.y=x2﹣(x+4)(x+2) B.y=2(x+1)(x﹣3)
C.y=ax2+bx+c D.y=
2.在△ABC和△DEF中,AB=3DE,AC=3DF,∠A=∠D.如果△ABC的周长为24,面积为18,则△DEF的周长、面积分别是( )
A.8,6 B.8,2 C.,6 D.,2
3.已知二次函数y=x2﹣6x+8,当0<x≤m时,﹣1≤y≤8,则m的值是( )
A.3 B.4 C.6 D.7
4.若2a=3b(a≠0),则的值为( )
A. B. C.2 D.3
5.下列命题中,是真命题的是( )
A.等腰三角形都相似 B.等边三角形都相似
C.锐角三角形都相似 D.直角三角形都相似
6.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(1)abc>0;(2)b<a+c;(3)4a+2b+c>0;(4)2c<3b;(5)a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共12小题,满分48分,每小题4分)
7.在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为 米.
8.如果抛物线y=ax2﹣1的顶点是它的最低点,那么a的取值范围是 .
9.抛物线y=x2﹣2x+3的对称轴是 .
10.若函数y=a(x﹣h)2+k(a≠0)的图象经过原点,最大值为16,且形状与抛物线y=﹣4x2+2x﹣3相同,则此函数的关系式为 .
11.已知二次函数y=﹣x2+2x+5,若P(n,y1),Q(n﹣2,y2)是该二次函数图象上的两点,且y1>y2,则实数n的取值范围为 .
12.化简:= .
13.已知一个直角三角形的两条直角边长分别为3和6,则该三角形的重心到其直角顶点的距离是 .
14.如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若=,则= .
15.如图是二次函数y=ax2+bx+c的部分图象,由图象可知方程ax2+bx+c=0的解是 , .
16.如图,正方形ABCD中,点E是边BC上一点,AE的垂直平分线分别交AB,BD,CD于点F,G,H.若GE=5,则FH的长为 .
17.如图,Rt△ABC中,∠ACB=90°,AC=3,AB=5,D为AB边上一动点,连接CD,△ACD与△A′CD关于直线CD轴对称,连接BA′,则BA′的最小值为 .
18.如图,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,PA=PD,∠APD=90°,= .
三.解答题(共7小题,满分78分)
19.(10分)已知==,求的值.
20.(10分)如图,已知二次函数y=ax2+bx+c的图象过点A(﹣1,0)和点C(0,3),对称轴为直线x=1.
(1)求该二次函数的关系式和顶点坐标;
(2)结合图象,当y<3时,直接写出x的取值范围.
21.(10分)如图,Rt△ABC中,∠ACB=90°,D是BC的中点,CE⊥AD,垂足为E.
(1)求证:CD2=DE AD;
(2)求证:∠BED=∠ABC.
22.(10分)已知:如图,梯形ABCD中,AD∥BC,AB=DC,点E在下底BC上,∠AED=∠B.
(1)求证:CE AD=DE2;
(2)求证:.
23.(12分)小强在地面E处放一面镜子,刚好能从镜子中看到教学楼的顶端B,此时EA=21米,CE=2.5米.已知眼睛距离地面的高度DC=1.6米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
24.(12分)在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0),B(3,0),过点B的直线y=x﹣2交抛物线于点C.
(1)求该抛物线的函数表达式;
(2)若点P是直线BC下方抛物线上的一个动点(P不与点B,C重合),求△PBC面积的最大值;
(3)若点M在抛物线上,将线段OM绕点O旋转90°,得到线段ON,是否存在点M,使点N恰好落在直线BC上?若存在,请直接写出点M的坐标;若不存在,请说明理由.
25.(14分)如图1,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.EC与BD相交于点G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AD=2,求tan∠E;
(3)如图2,连接AG,请在下面选择EG,DG,AG三者之间的数量关系并证明.我的选择是 .
①EG﹣DG=AG;②EG﹣DG=AG;③EG﹣DG=AG.
参考答案与试题解析
一.选择题(共6小题,满分24分,每小题4分)
1.解:A、y=x2﹣(x+4)(x+2)=x2﹣x2﹣6x﹣8=﹣6x﹣8,是一次函数,故本选项不合题意;
B、y=2(x+1)(x﹣3)=2(x2﹣2x﹣3)=2x2﹣4x﹣6,是二次函数,故本选项符合题意;
C、y=ax2+bx+c,不一定是二次函数,故本选项不合题意;
D、y=的右边是分式,不是二次函数,故本选项不合题意;
故选:B.
2.解:在△ABC和△DEF中,
∵AB=3DE,
∴=3,
∵AC=3DF,
∴=3,
∴=,
∵∠A=∠D,
∴△ABC∽△DEF,
∴==3,
∵△ABC的周长为24,
∴△DEF的周长=×24=8,
∴==32=9
∵S△ABC=18,
∴S△DEF=S△ABC=2.
故选:B.
3.解:∵二次函数y=x2﹣6x+8=(x﹣3)2﹣1,
∴该函数的对称轴是直线x=3,函数图象开口向上,当x=3时取得最小值﹣1,
∵当0<x≤m时,﹣1≤y≤8,当x=0时,y=8,当x=6时,y=8,
∴m=6,
故选:C.
4.解:∵2a=3b(a≠0),
∴a=b,
∴==2;
故选:C.
5.解:A、等腰三角形不一定相似,是假命题,故A选项错误;
B、等边三角形都相似,是真命题,故B选项正确;
C、锐角三角形不一定都相似,是假命题,故C选项错误;
D、直角三角形不一定都相似,是假命题,故D选项错误.
故选:B.
6.解:(1)图象开口向下,与y轴交于正半轴,对称轴为x=1,能得到:a<0,c>0,﹣=1,
∴b=﹣2a>0,
∴abc<0,此结论错误;
②当x=﹣1时,由图象知y<0,
把x=﹣1代入解析式得:a﹣b+c<0,
∴b>a+c,
∴此结论错误;
③图象开口向下,与y轴交于正半轴,对称轴为x=1,
能得到:a<0,c>0,﹣=1,
所以b=﹣2a,
所以4a+2b+c=4a﹣4a+c>0,
∴此结论正确;
④∵由①②知b=﹣2a且b>a+c,
∴2c<3b,此结论正确;
⑤当x=1时,y=a+b+c,
当x=m时,y=am2+bm+c,
∵m≠1的实数,图象开口向下,对称轴为x=1,
∴a+b+c>am2+bm+c,
∴a+b>m(am+b),
∴此结论正确.
故选:B.
二.填空题(共12小题,满分48分,每小题4分)
7.解:设A,B两地的实际距离为xcm,则:
1:2000=4.5:x,
解得x=9000.
9000cm=90m.
故答案为:90.
8.解:∵抛物线y=ax2﹣1的顶点是它的最低点,
∴抛物线的开口向上,
∴a>0,
故答案为a>0.
9.解:对称轴为直线,
∵a=1,b=﹣2,
∴对称轴为直线.
故答案为:直线x=1.
10.解:∵函数y=a(x﹣h)2+k的图象经过原点,
把(0,0)代入解析式,得:ah2+k=0,
∵最大值为16,即函数的开口向下,a<0,顶点的纵坐标k=16,
又∵形状与抛物线y=﹣4x2+2x﹣3相同,
∴二次项系数a=﹣4,
把a=﹣4,k=16代入y=a(x﹣h)2+k中,得h=±2,
∴函数解析式是:y=﹣4(x﹣2)2+16或y=﹣4(x+2)2+16,
即y=﹣4x2﹣16x或y=﹣4x2+16x,
故答案为:y=﹣4x2﹣16x或y=﹣4x2+16x.
11.解:∵P(n,y1),Q(n﹣2,y2)是函数y=﹣x2+2x+5的图象上的两点,且y1>y2,
∴﹣n2+2n+5>﹣(n﹣2)2+2(n﹣2)+5,
化简整理得,4n﹣8<0,
∴n<2,
∴实数n的取值范围为n<2.
故答案为:n<2.
12.解:∵=﹣=+=.
故答案为.
13.解:∵直角三角形的两条直角边长分别为3和6,
∴斜边的长度为=3,
∴该三角形的重心到其直角顶点的距离是××3=,
故答案为:.
14.解:∵M,N分别是DE,BC的中点,
∴AM、AN分别为△ADE、△ABC的中线,
∵△ADE∽△ABC,
∴==,
∴=()2=,
故答案为:.
15.解:由图象可知对称轴x=2,与x轴的一个交点横坐标是5,它到直线x=2的距离是3个单位长度,所以另外一个交点横坐标是﹣1.
所以x1=﹣1,x2=5.
故答案是:x1=﹣1,x2=5.
16.解:过点H作HM⊥AB,垂足为M,设FH交AE于N,连接AG,CG,如图
∵FH是AE的垂直平分线,
∴∠ANF=90°,AN=NE,AG=GE,
∴∠BAE+∠AFN=90°,
∵四边形ABCD是正方形,
∴∠ABC=∠ADC=∠BAD=90°,AB=AD=BC,
∴∠BAE+∠AEB=90°,
∴∠AFN=∠AEB,
∵HM⊥AB,
∴∠AMH=∠HMF=90°,
∴四边形ADHM是矩形,
∴AD=HM=AB,
在△ABE和△HMF中,
,
∴△ABE≌△HMF(AAS),
∴FH=AE,
∵G在AE的垂直平分线HF上,
∴GA=GE=5,
∵BD是正方形ABCD的对角线,
∴∠ABG=∠CBG=45°,
在△ABG和△CBG中,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,∠GAB=∠GCB,
∴GE=GC,
∴∠GEC=∠GCE,
∴∠GEC=∠GAB,
∵∠GEC+∠GEB=180°,
∴∠GAB+∠GEB=180°,
∴∠AGE=360°﹣∠ABE﹣(∠BAG+∠GEB)=360°﹣90°﹣180°=90°,
∵GA=GE=5,
在Rt△AGE中,AE==5,
∴FH=AE=5,
故答案为:5.
17.解:∵∠ACB=90°,AC=3,AB=5,
∴BC==4,
∵△ACD与△A′CD关于直线CD轴对称,
∴CA′=CA=3,
∵BA′≥BC﹣BA(当且仅当B、A′、C共线时取等号),
∴BA′的最小值为4﹣3=1.
故答案为1.
18.解:过点A作AE⊥BC于E,过点D作DF⊥BC于F,
由(1)可知,EF=AE+DF,
∵∠B=∠C=45°,AE⊥BC,DF⊥BC,
∴∠B=∠BAE=45°,∠C=∠CDF=45°,
∴BE=AE,CF=DF,AB=AE,CD=DF,
∴BC=BE+EF+CF=2(AE+DF),
∴==.
故答案为:.
三.解答题(共7小题,满分78分)
19.解:设===k(k≠0),
∴x=2k,y=3k,z=4k,
∴==.
20.解:(1)根据题意得,
解得,.
∴二次函数的关系式为:y=﹣x2+2x+3,
∵y=﹣(x﹣1)2+4,
∴二次函数的顶点坐标(1,4).
(2)当y=3时,3=﹣(x﹣1)2+4,
解得,x1=0或x2=2,
∵y<3,
∴x<0或x>2.
21.证明(1)∵CE⊥AD,
∴∠CED=∠ACB=90°,
∵∠CDE=∠ADC,
∴△CDE∽△ADC,
∴CD:AD=DE:CD,
∴CD2=DE AD.
(2)∵D是BC的中点,
∴BD=CD;
∵CD2=DE AD,
∴BD2=DE AD
∴BD:AD=DE:BD;
又∵∠ADB=∠BDE,
∴△BDE∽△ADB,
∴∠BED=∠ABC.
22.证明:(1)∵梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠C,AB=DC,∠ADE=∠DEC,
∵∠AED=∠B,
∴∠C=∠AED,
∴△ADE∽△DEC,
∴,
∴CE AD=DE2;
(2)∵△ADE∽△DEC,
∴=,
∴=,
∴.
23.解:根据题意得∠AEB=∠CED,
∵Rt△AEB∽Rt△CED,
∴=,即=,
解得:AB=13.44.
答:教学楼的高度为13.44m.
24.解:(1)将点A(﹣1,0),B(3,0)代入y=ax2+bx﹣3 中,得:
,
解得:,
∴该抛物线表达式为y=x2﹣2x﹣3.
(2)如图1,过点P作PD∥y轴,交x轴于点D,交BC于点E,作CF⊥PD于点F,连接PB,PC,
设点P(m,m2﹣2m﹣3),则点E (m,),
∴PE=PD﹣DE=﹣m2+2m+3﹣(﹣m+2)=﹣m2+m+1,
联立方程组:,
解得:,,
∵点B坐标为(3,0),
∴点C的坐标为(,﹣),
∴BD+CF=3+,
∴S△PBC=S△PEB+S△PEC
=PE BD+PE CF
=PE(BD+CF)
=(﹣m2+m+1)
=()2+,(其中<m<3),
∵,
∴这个二次函数有最大值.
当m=时,S△PBC的最大值为.
(3)如图2,设M(t,t2﹣2t﹣3),N(n, n﹣2),
作MG⊥y轴于点G,NH⊥x轴于H,
∴∠OGM=∠OHN=90°,
∵线段OM绕点O旋转90°,得到线段ON,
∴OM=ON,∠MON=90°,
∵∠GOH=90°,
∴∠MOG=∠NOH,
在△OGM与△OHN中,
,
∴△OGM≌△OHN(AAS),
∴GM=NH,OG=OH,
∴,
解得:,,
M1(0,﹣3),M2,
如图3,设M(t,t2﹣2t﹣3),N(n, n﹣2),
作MG⊥x轴于点G,NH⊥x轴于H,
∴∠OGM=∠OHN=90°,
∵线段OM绕点O旋转90°,得到线段ON,
∴OM=ON,∠MON=90°,
∵∠GOH=90°,
∴∠MOG=∠NOH,
在△OGM与△OHN中,
,
∴△OGM≌△OHN(AAS),
∴GM=NH,OG=OH,
∴,
解得:t1=,t2=,
∴M3,M4(,);
综上所述,点M的坐标为M1(0,﹣3),M2,M3,M4(,).
25.(1)证明:∵四边形ABCD是矩形,点E在BA的延长线上,
∴∠EAF=∠DAB=90°,
又∵AE=AD,AF=AB,
∴△AEF≌△ADB(SAS),
∴∠AEF=∠ADB,
∴∠GEB+∠GBE=∠ADB+∠ABD=90°,
即∠EGB=90°,
∴BD⊥EC;
(2)解:∵AD=2,
∴AE=AD=2,
∵四边形ABCD是矩形,
∴AE∥CD,
∴∠AEF=∠DCF,∠EAF=∠CDF,
∴△AEF∽△DCF,
∴=,
∴AE DF=AF DC,
设AF=AB=a(a>0),则2(2﹣a)=a2,
整理得:a2+2a﹣4=0,
解得:a=﹣1+或﹣1﹣(舍去),
∴AF=﹣1+,
∴tanE==;
(3)解:我的选择是:②EG﹣DG=AG,证明如下:
在线段EG上取点P,使得EP=DG,连接AP,如图2所示:
∵AE=AD,∠AEP=∠ADG,EP=DG,
∴△AEP≌△ADG(SAS),
∴AP=AG,∠EAP=∠DAG,
∴∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,
∴△PAG为等腰直角三角形,
∴PG=AG,
∴EG﹣DG=EG﹣EP=PG=AG,
故答案为:②EG﹣DG=AG.
同课章节目录
