2021-2022学年人教五四新版七年级上册数学期中复习试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年人教五四新版七年级上册数学期中复习试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 288.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 08:13:39 | ||
图片预览


文档简介
2021-2022学年人教五四新版七年级上册数学期中复习试卷
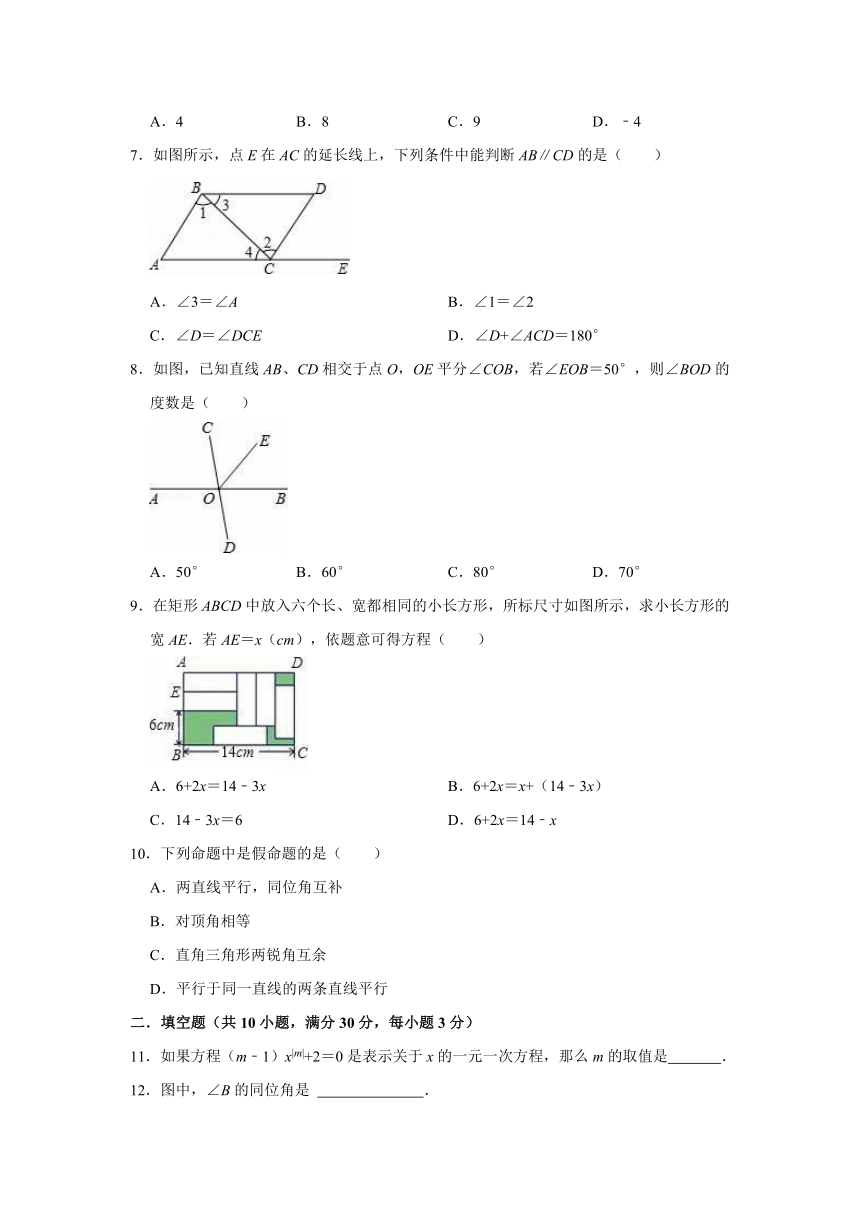
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程中:①2x+4=6,②x﹣1=,③3x2﹣2x,④5x<7,⑤3x﹣2y=2,⑥x=3,其中是一元一次方程的有( )
A.5个 B.4个 C.3个 D.2个
2.下列图形中,不能通过其中一个四边形平移得到的是( )
A. B.
C. D.
3.下列图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
4.下列等式变形正确的是( )
A.若﹣3x=5,则x=﹣
B.若,则2x+3(x﹣1)=1
C.若5x﹣6=2x+8,则5x+2x=8+6
D.若3(x+1)﹣2x=1,则3x+3﹣2x=1
5.如图,直线a∥b,∠1=40°,则∠2=( )
A.40° B.60° C.100° D.140°
6.如果x=3是方程2x+3a=6x的解,那么a的值是( )
A.4 B.8 C.9 D.﹣4
7.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
8.如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=50°,则∠BOD的度数是( )
A.50° B.60° C.80° D.70°
9.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x B.6+2x=x+(14﹣3x)
C.14﹣3x=6 D.6+2x=14﹣x
10.下列命题中是假命题的是( )
A.两直线平行,同位角互补
B.对顶角相等
C.直角三角形两锐角互余
D.平行于同一直线的两条直线平行
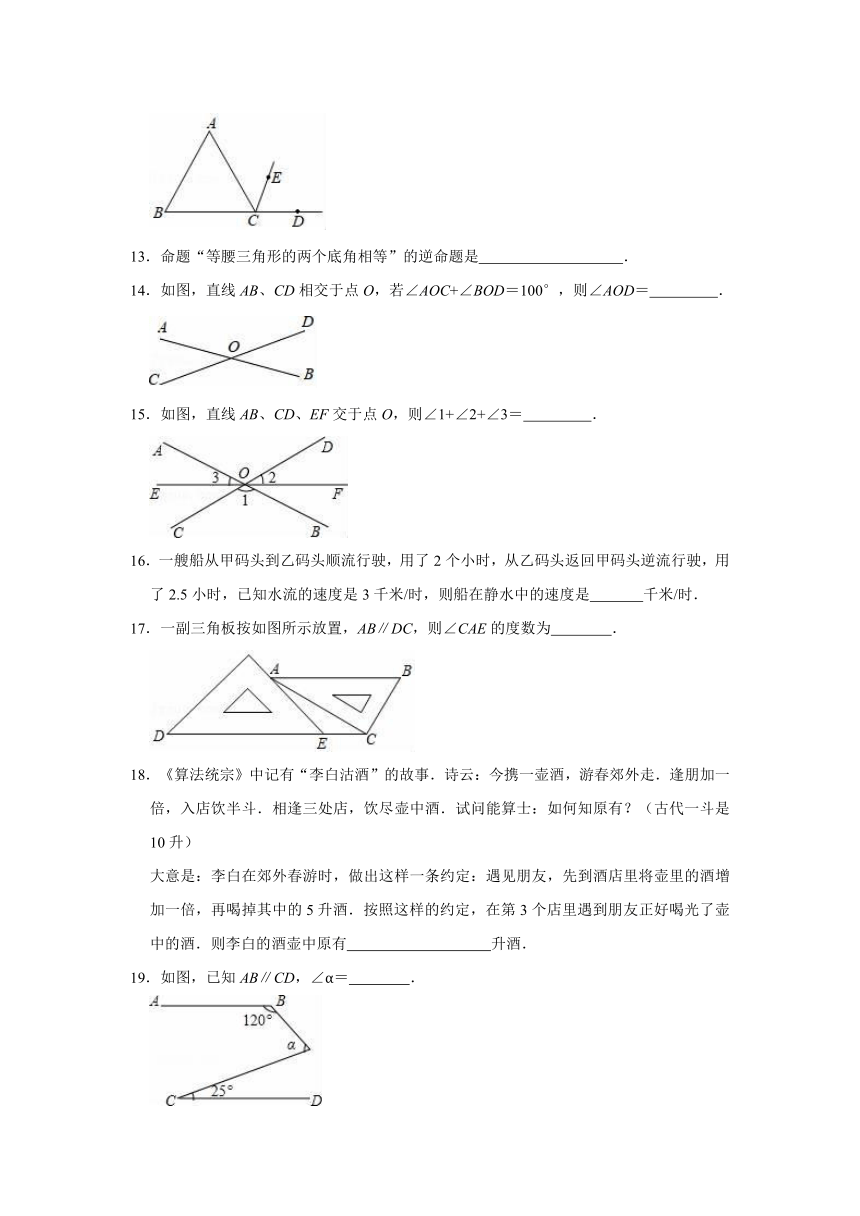
二.填空题(共10小题,满分30分,每小题3分)
11.如果方程(m﹣1)x|m|+2=0是表示关于x的一元一次方程,那么m的取值是 .
12.图中,∠B的同位角是 .
13.命题“等腰三角形的两个底角相等”的逆命题是 .
14.如图,直线AB、CD相交于点O,若∠AOC+∠BOD=100°,则∠AOD= .
15.如图,直线AB、CD、EF交于点O,则∠1+∠2+∠3= .
16.一艘船从甲码头到乙码头顺流行驶,用了2个小时,从乙码头返回甲码头逆流行驶,用了2.5小时,已知水流的速度是3千米/时,则船在静水中的速度是 千米/时.
17.一副三角板按如图所示放置,AB∥DC,则∠CAE的度数为 .
18.《算法统宗》中记有“李白沽酒”的故事.诗云:今携一壶酒,游春郊外走.逢朋加一倍,入店饮半斗.相逢三处店,饮尽壶中酒.试问能算士:如何知原有?(古代一斗是10升)
大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒.则李白的酒壶中原有 升酒.
19.如图,已知AB∥CD,∠α= .
20.小韩和同学们在一家快餐店吃饭,下表为快餐店的菜单:
种类 配餐 价格(元) 优惠活动
A餐 1份盖饭 20 消费满150元,减24元消费满300元,减48元…
B餐 1份盖饭+1杯饮料 28
C餐 1份盖饭+1杯饮料+1份小菜 32
小韩记录大家的点餐种类,并根据菜单一次点好,已知他们所点的餐共有11份盖饭,x杯饮料和5份小菜,
(1)他们共点了 份B餐.
(2)若他们至少需要6杯饮料,要使所花费的钱数最少,则应该点 份B餐.
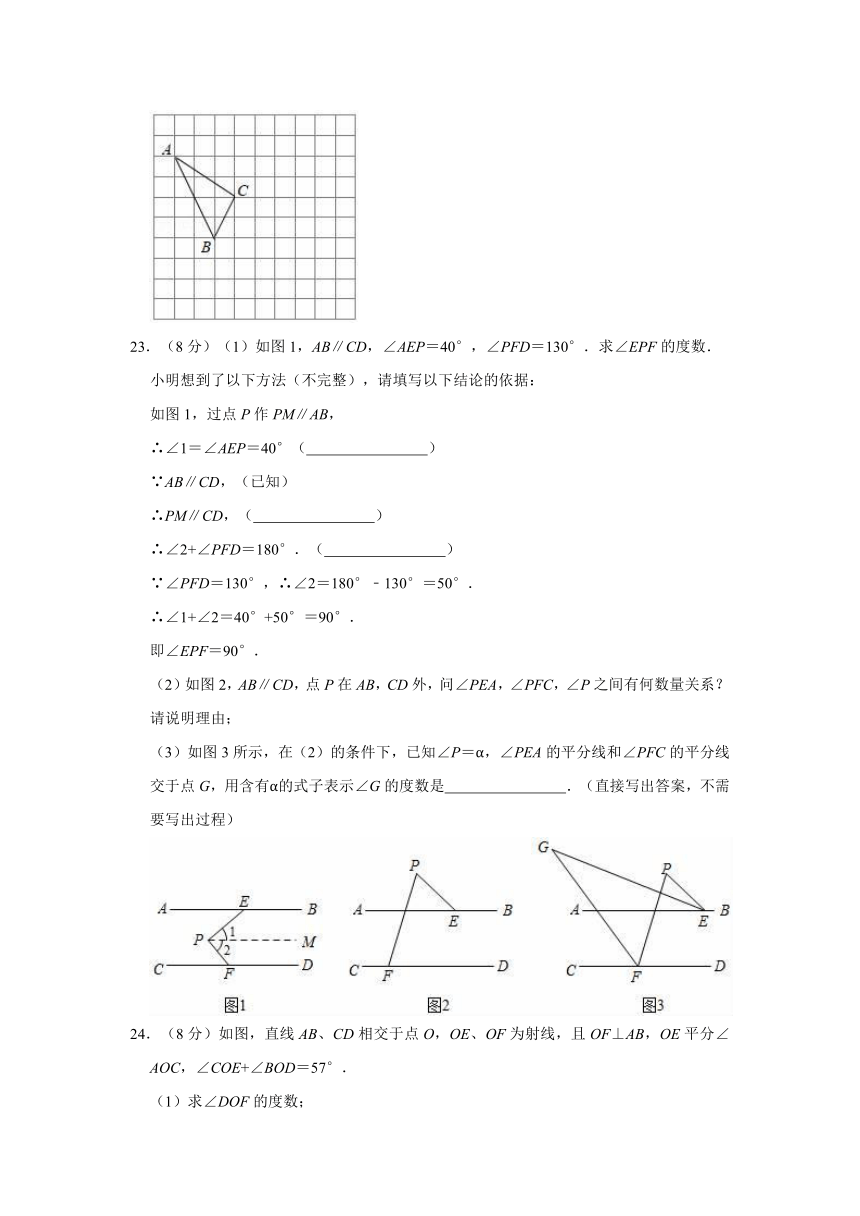
三.解答题(共7小题,满分60分)
21.(7分)解方程:
(1)3x+7=32﹣2x;
(2)4x﹣3(20﹣x)+4=0;
(3);
(4)=2﹣.
22.(7分)如图,在正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在如图所示的网格平面内画出平面直角坐标系;
(2)点P(m,n)是△ABC边BC上任意一点,三角形经过平移后得到△A1B1C1,点P的对应点为P1(m+6,n﹣2).
①直接写出点B1的坐标 ;
②画出△ABC平移后的△A1B1C1.
(3)在y轴上是否存在点P,使△AOP的面积等于△ABC面积的,若存在,请求出点P的坐标;若不存在,请说明理由.
23.(8分)(1)如图1,AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数.
小明想到了以下方法(不完整),请填写以下结论的依据:
如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°( )
∵AB∥CD,(已知)
∴PM∥CD,( )
∴∠2+∠PFD=180°.( )
∵∠PFD=130°,∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
(2)如图2,AB∥CD,点P在AB,CD外,问∠PEA,∠PFC,∠P之间有何数量关系?请说明理由;
(3)如图3所示,在(2)的条件下,已知∠P=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数是 .(直接写出答案,不需要写出过程)
24.(8分)如图,直线AB、CD相交于点O,OE、OF为射线,且OF⊥AB,OE平分∠AOC,∠COE+∠BOD=57°.
(1)求∠DOF的度数;
(2)请你直接写出图中4对相等的角(直角、平角除外).
25.(10分)十一前夕,某商场从厂家购进了甲、乙两种商品,甲种商品每件的进价比乙种商品每件的进价多20元.购进甲种商品4件与购进乙种商品5件的进价相同.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)该商场从厂家购进了甲、乙两种商品共50件,所用资金恰好为4600元.出售时,甲种商品在进价的基础上加价40%进行标价;乙商品按标价出售,则每件可获利30元.若按标价出售甲、乙两种商品,则全部售出后共可获利多少元?
(3)在(2)的条件下,十一期间,甲商品按标价的九折出售,乙商品按标价出售一部分商品后进行促销,按标价的九折再让利4元出售,甲、乙两种商品全部售出,总获利比全部按标价售出获利少了,则乙商品按标价售出多少件?
26.(10分)“水是生命之源”,某自来水公司为鼓励用户节约用水,按以下规定收取水费:
月用水量/吨 单价(元/吨)
不超过20吨的部分 2
超过20吨的部分 2.5
另:每吨水加收0.3元的城市污水处理费
(1)若某用户11月份共用水25吨,他应缴水费多少元?
(2)若该用户的水表有故障,每次用水只有60%计入用水量,在这样的情况下12月份共缴水费41.4元,则该用户12月份实际用水多少吨?
27.(10分)已知,AB∥CD,点E在CD上,点G,F在AB上,点H在AB,CD之间,连接FE,EH,HG,∠AGH=∠FED,FE⊥HE,垂足为E.
(1)如图1,求证:HG⊥HE;
(2)如图2,GM平分∠HGB,EM平分∠HED,GM,EM交于点M,求证:∠GHE=2∠GME;
(3)如图3,在(2)的条件下,FK平分∠AFE交CD于点K,若∠KFE:∠MGH=13:5,求∠HED的度数.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:①2x+4=6是一元一次方程;
②x﹣1=是分式方程;
③3x2﹣2x不是方程,是代数式;
④5x<7是一元一次不等式;
⑤3x﹣2y=2是二元一次方程;
⑥x=3是一元一次方程;
一元一次方程共2个,
故选:D.
2.解:A、能通过其中一个四边形平移得到,故本选项不符合题意;
B、能通过其中一个四边形平移得到,故本选项不符合题意;
C、能通过其中一个四边形平移得到,故本选项不符合题意;
D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,故本选项符合题意.
故选:D.
3.解:A、∠1与∠2的两边不是互为反向延长线,不符合对顶角的定义,不是对顶角,故本选项不符合题意;
B、∠1与∠2的两边一边互为反向延长线,另一边不是互为反向延长线,不符合对顶角的定义,不是对顶角,故本选项不符合题意;
C、∠1与∠2没有公共顶点,不符合对顶角的定义,不是对顶角,故本选项不符合题意;
D、∠1与∠2符合对顶角的定义,是对顶角,故本选项符合题意;
故选:D.
4.解:A、若﹣3x=5,则x=﹣,错误,故本选项不符合题意;
B、若,则2x+3(x﹣1)=6,错误,故本选项不符合题意;
C、若5x﹣6=2x+8,则5x﹣2x=8+6,错误,故本选项不符合题意;
D、若3(x+1)﹣2x=1,则3x+3﹣2x=1,正确,故本选项符合题意;
故选:D.
5.解:如图,
∵a∥b,
∴∠1=∠3=40°;
∵∠2+∠3=180°,
∴∠2=140°.
故选:D.
6.解:把x=3代入2x+3a=6x得:
2×3+3a=6×3,
解得:a=4.
故选:A.
7.解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
8.解:∵OE平分∠COB,
∴∠EOB=∠COE,
∵∠EOB=50°,
∴∠COB=100°,
∴∠BOD=180°﹣100°=80°.
故选:C.
9.解:设AE为xcm,则AM为(14﹣3x)cm,
根据题意得出:∵AN=MW,∴AN+6=x+MR,
即6+2x=x+(14﹣3x)
故选:B.
10.解:A、两直线平行,同位角相等,故本选项说法是假命题;
B、对顶角相等,本选项说法是真命题;
C、直角三角形两锐角互余,本选项说法是真命题;
D、平行于同一直线的两条直线平行,本选项说法是真命题;
故选:A.
二.填空题(共10小题,满分30分,每小题3分)
11.解:由一元一次方程的特点得,
解得m=﹣1.
故填:﹣1.
12.解:∠B与∠ECD是直线AB、CE被直线BD所截的一组同位角,
∠B与∠ACD是直线AB、AC被直线BD所截的一组同位角,
故答案为:∠ECD,∠ACD.
13.解:因为原命题的题设是:“一个三角形是等腰三角形”,结论是“这个三角形两底角相等”,
所以命题“等腰三角形的两个底角相等”的逆命题是“两个角相等三角形是等腰三角形”.
14.解:∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD,
又∵∠AOC+∠BOD=100°,
∴∠AOC=50°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°﹣∠AOC
=180°﹣50°
=130°.
故答案为:130°.
15.解:∵∠3与∠BOF是对顶角,
∴∠3=∠BOF,
∵∠1+∠2+∠BOF=180°,
∴∠1+∠2+∠3=180°.
故答案为:180°.
16.解:设船在静水中的速度是x,则顺流时的速度为(x+3)km/h,逆流时的速度为(x﹣3)km/h,
由题意得,2(x+3)=2.5(x﹣3),
解得:x=27,
即船在静水中的速度是27千米/时.
故答案为:27.
17.解:由图可知,
∠1=45°,∠2=30°,
∵AB∥DC,
∴∠BAE=∠1=45°,
∴∠CAE=∠BAE﹣∠2=45°﹣30°=15°,
故答案为:15°.
18.解:设壶中原有x升酒,
根据题意得:2[2(2x﹣5)﹣5]=5,
解得:x=.
答:壶中原有升酒.
故答案为:.
19.解:如图,过∠α的顶点作AB的平行线EF,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1=180°﹣120°=60°,
∠2=25°,
∴∠α=∠1+∠2=60°+25°=85°.
故答案为:85°.
20.解:(1)∵三种套餐中均包含盖饭且只有C餐中含小菜,有5份小菜,
∴C餐中含5杯饮料,
∵只有A餐中不含小菜,
∴他们点了(x﹣5)份B餐.
故答案为:(x﹣5).
(2)∵三种餐中均包含盖饭且只有C餐中含小菜,
∴点了5份C餐,
∵B餐,C餐都有1份盖饭,
∴B餐,C餐共有盖饭x份,
∴A餐共有(11﹣x),
一共花费:
20(11﹣x)+28(x﹣5)+32×5
=220﹣20x+28x﹣140+160
=8x+240(6≤x≤11),
当x=6时,原式=8×6+240=288,
288﹣24=264(元);
当x=7时,原式=8×7+240=296,
296﹣24=272(元);
当x=8时,原式=8×8+240=304,
208﹣48=256(元);
当x=9时,原式=8×9+240=312,
212﹣48=264(元);
当x=10时,原式=8×10+240=320,
320﹣48=272(元);
当x=11时,原式=8×11+240=328,
328﹣48=280(元).
综上所述,当x=8时,所花费的钱数最少,应该点8﹣5=3份B餐.
故答案为:(x﹣5);3.
三.解答题(共7小题,满分60分)
21.解:(1)3x+7=32﹣2x,
3x+2x=32﹣7,
5x=25,
x=5;
(2)4x﹣3(20﹣x)+4=0,
4x﹣60+3x+4=0,
4x+3x=60﹣4,
7x=56,
x=8;
(3)去分母得:3(3x+5)=2(2x﹣1),
9x+15=4x﹣2,
9x﹣4x=﹣2﹣15,
5x=﹣17,
x=﹣3.4;
(4)去分母得:4(5y+4)+3(y﹣1)=24﹣(5y﹣3),
20y+16+3y﹣3=24﹣5y+3,
20y+3y+5y=24+3﹣16+3,
28y=14,
y=.
22.解:(1)如图,平面直角坐标系如图所示:
(2)①B1(4,﹣1).
故答案为(4,﹣1).
②如图,△A1B1C1即为所求.
(3)设P(0,m).
由题意,×|m|×4=×(3×4﹣×2×4﹣×2×3﹣×1×2),
解得m=±,
∴P(0,)或(0,﹣).
23.解:(1)如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°.(两直线平行,内错角相等)
∵AB∥CD,(已知)
∴PM∥CD,(平行于同一条直线的两直线平行)
∴∠2+∠PFD=180°. (两直线平行,同旁内角互补)
∵∠PFD=130°,
∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
故答案为:两直线平行,内错角相等;平行于同一条直线的两直线平行;两直线平行,同旁内角互补;
(2)∠PFC=∠PEA+∠P.
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)令AB与PF交点为O,连接EF,如图3.
在△GFE中,∠G=180°﹣(∠GFE+∠GEF),
∵∠GEF=PEA+∠OEF,∠GFE=PFC+∠OFE,
∴∠GEF+∠GFE=PEA+∠OEF+PFC+∠OFE,
∵由(2)知∠PFC=∠PEA+∠P,
∴∠PEA=∠PFC﹣α,
∵∠OFE+∠OEF=180°﹣∠FOE=180°﹣∠PFC,
∴∠GEF+∠GFE=(∠PFC﹣α)+∠PFC+180°﹣∠PFC=180°﹣α,
∴∠G=180°﹣(∠GEF+∠GFE)=180°﹣180°+α=α.
故答案为:α.
24.解:(1)∵OF⊥AB,
∴∠BOF=∠AOF=90°
∵OE平分∠AOC,
∴∠AOE=∠COE=∠AOC,
又∵∠AOC=∠BOD,∠COE+∠BOD=57°.
∴∠AOE=∠COE=×57°=19°,
∴∠AOC=∠BOD=38°,
∴∠DOF=∠BOD+∠BOF=38°+90°=128°,
(2)由对顶角相等可得∠AOC=∠BOD,∠AOD=∠BOC,
由角平分线的定义可得∠AOE=∠COE,
∵∠BOE+∠AOE=180°=∠DOE+∠COE,
而∠AOE=∠COE,
∴∠BOE=∠DOE,
故图中相等的角有∠AOE=∠COE,∠AOC=∠BOD,∠AOD=∠∠BOC,∠BOE=∠DOE.
25.解:(1)设乙种商品每件的进价是x元,则甲种商品每件的进价是(x+20)元,依题意有
4(x+20)=5x,
解得x=80,
则x+20=80+20=100.
故甲种商品每件的进价是100元,乙种商品每件的进价是80元;
(2)设该商场从厂家购进了甲种商品y件,则乙种商品(50﹣y)件,依题意有
100y+80(50﹣y)=4600,
解得y=30,
则50﹣y=50﹣30=20,
则100×40%×30+30×20=1800(元).
故全部售出后共可获利1800元;
(3)设乙商品按标价售出z件,则乙商品按促销价售出(20﹣z)件,依题意有
(100+100×40%)×0.9×30+(80+30)z+[(80+30)×0.9﹣4](20﹣z)=4600+1800×(1﹣),
解得z=8.
故乙商品按标价售出8件.
26.解:(1)20×2+(25﹣20)×2.5+0.3×25=60(元),
答:他应缴水费60元.
(2)∵20×2+0.3×20=46>41.4,
故水表有故障时,计入用水量不超过20吨,
设该用户12月份实际用水x吨,
由题意,得2×60%x+0.3×60%x=41.4,
解得x=30,
答:该用户12月份实际用水30吨.
27.证明:(1)∵AB∥CD,
∴∠AFE=∠FED,
∵∠AGH=∠FED,
∴∠AFE=∠AGH,
∴EF∥GH,
∴∠FEH+∠H=180°,
∵FE⊥HE,
∴∠FEH=90°,
∴∠H=180°﹣∠FEH=90°,
∴HG⊥HE;
(2)过点M作MQ∥AB,
∵AB∥CD,
∴MQ∥CD,
过点H作HP∥AB,
∵AB∥CD,
∴HP∥CD,
∵GM平分∠HGB,
∴∠BGM=∠HGM=∠BGH,
∵EM平分∠HED,
∴∠HEM=∠DEM=∠HED,
∵MQ∥AB,
∴∠BGM=∠GMQ,
∵MQ∥CD,
∴∠QME=∠MED,
∴∠GME=∠GMQ+∠QME=∠BGM+∠MED,
∵HP∥AB,
∴∠BGH=∠GHP=2∠BGM,
∵HP∥CD,
∴∠PHE=∠HED=2∠MED,
∴∠GHE=∠GHP+∠PHE=2∠BGM+2∠MED=2(∠BGM+∠MED),
∴∠GHE=∠2GME;
(3)过点M作MQ∥AB,过点H作HP∥AB,
由∠KFE:∠MGH=13:5,设∠KFE=13x,∠MGH=5x,
由(2)可知:∠BGH=2∠MGH=10x,
∵∠AFE+∠BFE=180°,
∴∠AFE=180°﹣10x,
∵FK平分∠AFE,
∴∠AFK=∠KFE=∠AFE,
即,
解得:x=5°,
∴∠BGH=10x=50°,
∵HP∥AB,HP∥CD,
∴∠BGH=∠GHP=50°,∠PHE=∠HED,
∵∠GHE=90°,
∴∠PHE=∠GHE﹣∠GHP=90°﹣50°=40°,
∴∠HED=40°.
一.选择题(共10小题,满分30分,每小题3分)
1.下列方程中:①2x+4=6,②x﹣1=,③3x2﹣2x,④5x<7,⑤3x﹣2y=2,⑥x=3,其中是一元一次方程的有( )
A.5个 B.4个 C.3个 D.2个
2.下列图形中,不能通过其中一个四边形平移得到的是( )
A. B.
C. D.
3.下列图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
4.下列等式变形正确的是( )
A.若﹣3x=5,则x=﹣
B.若,则2x+3(x﹣1)=1
C.若5x﹣6=2x+8,则5x+2x=8+6
D.若3(x+1)﹣2x=1,则3x+3﹣2x=1
5.如图,直线a∥b,∠1=40°,则∠2=( )
A.40° B.60° C.100° D.140°
6.如果x=3是方程2x+3a=6x的解,那么a的值是( )
A.4 B.8 C.9 D.﹣4
7.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
8.如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠EOB=50°,则∠BOD的度数是( )
A.50° B.60° C.80° D.70°
9.在矩形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若AE=x(cm),依题意可得方程( )
A.6+2x=14﹣3x B.6+2x=x+(14﹣3x)
C.14﹣3x=6 D.6+2x=14﹣x
10.下列命题中是假命题的是( )
A.两直线平行,同位角互补
B.对顶角相等
C.直角三角形两锐角互余
D.平行于同一直线的两条直线平行
二.填空题(共10小题,满分30分,每小题3分)
11.如果方程(m﹣1)x|m|+2=0是表示关于x的一元一次方程,那么m的取值是 .
12.图中,∠B的同位角是 .
13.命题“等腰三角形的两个底角相等”的逆命题是 .
14.如图,直线AB、CD相交于点O,若∠AOC+∠BOD=100°,则∠AOD= .
15.如图,直线AB、CD、EF交于点O,则∠1+∠2+∠3= .
16.一艘船从甲码头到乙码头顺流行驶,用了2个小时,从乙码头返回甲码头逆流行驶,用了2.5小时,已知水流的速度是3千米/时,则船在静水中的速度是 千米/时.
17.一副三角板按如图所示放置,AB∥DC,则∠CAE的度数为 .
18.《算法统宗》中记有“李白沽酒”的故事.诗云:今携一壶酒,游春郊外走.逢朋加一倍,入店饮半斗.相逢三处店,饮尽壶中酒.试问能算士:如何知原有?(古代一斗是10升)
大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒.则李白的酒壶中原有 升酒.
19.如图,已知AB∥CD,∠α= .
20.小韩和同学们在一家快餐店吃饭,下表为快餐店的菜单:
种类 配餐 价格(元) 优惠活动
A餐 1份盖饭 20 消费满150元,减24元消费满300元,减48元…
B餐 1份盖饭+1杯饮料 28
C餐 1份盖饭+1杯饮料+1份小菜 32
小韩记录大家的点餐种类,并根据菜单一次点好,已知他们所点的餐共有11份盖饭,x杯饮料和5份小菜,
(1)他们共点了 份B餐.
(2)若他们至少需要6杯饮料,要使所花费的钱数最少,则应该点 份B餐.
三.解答题(共7小题,满分60分)
21.(7分)解方程:
(1)3x+7=32﹣2x;
(2)4x﹣3(20﹣x)+4=0;
(3);
(4)=2﹣.
22.(7分)如图,在正方形网格中,每个小正方形的边长均为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(﹣4,5)、(﹣1,3).
(1)请在如图所示的网格平面内画出平面直角坐标系;
(2)点P(m,n)是△ABC边BC上任意一点,三角形经过平移后得到△A1B1C1,点P的对应点为P1(m+6,n﹣2).
①直接写出点B1的坐标 ;
②画出△ABC平移后的△A1B1C1.
(3)在y轴上是否存在点P,使△AOP的面积等于△ABC面积的,若存在,请求出点P的坐标;若不存在,请说明理由.
23.(8分)(1)如图1,AB∥CD,∠AEP=40°,∠PFD=130°.求∠EPF的度数.
小明想到了以下方法(不完整),请填写以下结论的依据:
如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°( )
∵AB∥CD,(已知)
∴PM∥CD,( )
∴∠2+∠PFD=180°.( )
∵∠PFD=130°,∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
(2)如图2,AB∥CD,点P在AB,CD外,问∠PEA,∠PFC,∠P之间有何数量关系?请说明理由;
(3)如图3所示,在(2)的条件下,已知∠P=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数是 .(直接写出答案,不需要写出过程)
24.(8分)如图,直线AB、CD相交于点O,OE、OF为射线,且OF⊥AB,OE平分∠AOC,∠COE+∠BOD=57°.
(1)求∠DOF的度数;
(2)请你直接写出图中4对相等的角(直角、平角除外).
25.(10分)十一前夕,某商场从厂家购进了甲、乙两种商品,甲种商品每件的进价比乙种商品每件的进价多20元.购进甲种商品4件与购进乙种商品5件的进价相同.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)该商场从厂家购进了甲、乙两种商品共50件,所用资金恰好为4600元.出售时,甲种商品在进价的基础上加价40%进行标价;乙商品按标价出售,则每件可获利30元.若按标价出售甲、乙两种商品,则全部售出后共可获利多少元?
(3)在(2)的条件下,十一期间,甲商品按标价的九折出售,乙商品按标价出售一部分商品后进行促销,按标价的九折再让利4元出售,甲、乙两种商品全部售出,总获利比全部按标价售出获利少了,则乙商品按标价售出多少件?
26.(10分)“水是生命之源”,某自来水公司为鼓励用户节约用水,按以下规定收取水费:
月用水量/吨 单价(元/吨)
不超过20吨的部分 2
超过20吨的部分 2.5
另:每吨水加收0.3元的城市污水处理费
(1)若某用户11月份共用水25吨,他应缴水费多少元?
(2)若该用户的水表有故障,每次用水只有60%计入用水量,在这样的情况下12月份共缴水费41.4元,则该用户12月份实际用水多少吨?
27.(10分)已知,AB∥CD,点E在CD上,点G,F在AB上,点H在AB,CD之间,连接FE,EH,HG,∠AGH=∠FED,FE⊥HE,垂足为E.
(1)如图1,求证:HG⊥HE;
(2)如图2,GM平分∠HGB,EM平分∠HED,GM,EM交于点M,求证:∠GHE=2∠GME;
(3)如图3,在(2)的条件下,FK平分∠AFE交CD于点K,若∠KFE:∠MGH=13:5,求∠HED的度数.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:①2x+4=6是一元一次方程;
②x﹣1=是分式方程;
③3x2﹣2x不是方程,是代数式;
④5x<7是一元一次不等式;
⑤3x﹣2y=2是二元一次方程;
⑥x=3是一元一次方程;
一元一次方程共2个,
故选:D.
2.解:A、能通过其中一个四边形平移得到,故本选项不符合题意;
B、能通过其中一个四边形平移得到,故本选项不符合题意;
C、能通过其中一个四边形平移得到,故本选项不符合题意;
D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,故本选项符合题意.
故选:D.
3.解:A、∠1与∠2的两边不是互为反向延长线,不符合对顶角的定义,不是对顶角,故本选项不符合题意;
B、∠1与∠2的两边一边互为反向延长线,另一边不是互为反向延长线,不符合对顶角的定义,不是对顶角,故本选项不符合题意;
C、∠1与∠2没有公共顶点,不符合对顶角的定义,不是对顶角,故本选项不符合题意;
D、∠1与∠2符合对顶角的定义,是对顶角,故本选项符合题意;
故选:D.
4.解:A、若﹣3x=5,则x=﹣,错误,故本选项不符合题意;
B、若,则2x+3(x﹣1)=6,错误,故本选项不符合题意;
C、若5x﹣6=2x+8,则5x﹣2x=8+6,错误,故本选项不符合题意;
D、若3(x+1)﹣2x=1,则3x+3﹣2x=1,正确,故本选项符合题意;
故选:D.
5.解:如图,
∵a∥b,
∴∠1=∠3=40°;
∵∠2+∠3=180°,
∴∠2=140°.
故选:D.
6.解:把x=3代入2x+3a=6x得:
2×3+3a=6×3,
解得:a=4.
故选:A.
7.解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
8.解:∵OE平分∠COB,
∴∠EOB=∠COE,
∵∠EOB=50°,
∴∠COB=100°,
∴∠BOD=180°﹣100°=80°.
故选:C.
9.解:设AE为xcm,则AM为(14﹣3x)cm,
根据题意得出:∵AN=MW,∴AN+6=x+MR,
即6+2x=x+(14﹣3x)
故选:B.
10.解:A、两直线平行,同位角相等,故本选项说法是假命题;
B、对顶角相等,本选项说法是真命题;
C、直角三角形两锐角互余,本选项说法是真命题;
D、平行于同一直线的两条直线平行,本选项说法是真命题;
故选:A.
二.填空题(共10小题,满分30分,每小题3分)
11.解:由一元一次方程的特点得,
解得m=﹣1.
故填:﹣1.
12.解:∠B与∠ECD是直线AB、CE被直线BD所截的一组同位角,
∠B与∠ACD是直线AB、AC被直线BD所截的一组同位角,
故答案为:∠ECD,∠ACD.
13.解:因为原命题的题设是:“一个三角形是等腰三角形”,结论是“这个三角形两底角相等”,
所以命题“等腰三角形的两个底角相等”的逆命题是“两个角相等三角形是等腰三角形”.
14.解:∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD,
又∵∠AOC+∠BOD=100°,
∴∠AOC=50°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°﹣∠AOC
=180°﹣50°
=130°.
故答案为:130°.
15.解:∵∠3与∠BOF是对顶角,
∴∠3=∠BOF,
∵∠1+∠2+∠BOF=180°,
∴∠1+∠2+∠3=180°.
故答案为:180°.
16.解:设船在静水中的速度是x,则顺流时的速度为(x+3)km/h,逆流时的速度为(x﹣3)km/h,
由题意得,2(x+3)=2.5(x﹣3),
解得:x=27,
即船在静水中的速度是27千米/时.
故答案为:27.
17.解:由图可知,
∠1=45°,∠2=30°,
∵AB∥DC,
∴∠BAE=∠1=45°,
∴∠CAE=∠BAE﹣∠2=45°﹣30°=15°,
故答案为:15°.
18.解:设壶中原有x升酒,
根据题意得:2[2(2x﹣5)﹣5]=5,
解得:x=.
答:壶中原有升酒.
故答案为:.
19.解:如图,过∠α的顶点作AB的平行线EF,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1=180°﹣120°=60°,
∠2=25°,
∴∠α=∠1+∠2=60°+25°=85°.
故答案为:85°.
20.解:(1)∵三种套餐中均包含盖饭且只有C餐中含小菜,有5份小菜,
∴C餐中含5杯饮料,
∵只有A餐中不含小菜,
∴他们点了(x﹣5)份B餐.
故答案为:(x﹣5).
(2)∵三种餐中均包含盖饭且只有C餐中含小菜,
∴点了5份C餐,
∵B餐,C餐都有1份盖饭,
∴B餐,C餐共有盖饭x份,
∴A餐共有(11﹣x),
一共花费:
20(11﹣x)+28(x﹣5)+32×5
=220﹣20x+28x﹣140+160
=8x+240(6≤x≤11),
当x=6时,原式=8×6+240=288,
288﹣24=264(元);
当x=7时,原式=8×7+240=296,
296﹣24=272(元);
当x=8时,原式=8×8+240=304,
208﹣48=256(元);
当x=9时,原式=8×9+240=312,
212﹣48=264(元);
当x=10时,原式=8×10+240=320,
320﹣48=272(元);
当x=11时,原式=8×11+240=328,
328﹣48=280(元).
综上所述,当x=8时,所花费的钱数最少,应该点8﹣5=3份B餐.
故答案为:(x﹣5);3.
三.解答题(共7小题,满分60分)
21.解:(1)3x+7=32﹣2x,
3x+2x=32﹣7,
5x=25,
x=5;
(2)4x﹣3(20﹣x)+4=0,
4x﹣60+3x+4=0,
4x+3x=60﹣4,
7x=56,
x=8;
(3)去分母得:3(3x+5)=2(2x﹣1),
9x+15=4x﹣2,
9x﹣4x=﹣2﹣15,
5x=﹣17,
x=﹣3.4;
(4)去分母得:4(5y+4)+3(y﹣1)=24﹣(5y﹣3),
20y+16+3y﹣3=24﹣5y+3,
20y+3y+5y=24+3﹣16+3,
28y=14,
y=.
22.解:(1)如图,平面直角坐标系如图所示:
(2)①B1(4,﹣1).
故答案为(4,﹣1).
②如图,△A1B1C1即为所求.
(3)设P(0,m).
由题意,×|m|×4=×(3×4﹣×2×4﹣×2×3﹣×1×2),
解得m=±,
∴P(0,)或(0,﹣).
23.解:(1)如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°.(两直线平行,内错角相等)
∵AB∥CD,(已知)
∴PM∥CD,(平行于同一条直线的两直线平行)
∴∠2+∠PFD=180°. (两直线平行,同旁内角互补)
∵∠PFD=130°,
∴∠2=180°﹣130°=50°.
∴∠1+∠2=40°+50°=90°.
即∠EPF=90°.
故答案为:两直线平行,内错角相等;平行于同一条直线的两直线平行;两直线平行,同旁内角互补;
(2)∠PFC=∠PEA+∠P.
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)令AB与PF交点为O,连接EF,如图3.
在△GFE中,∠G=180°﹣(∠GFE+∠GEF),
∵∠GEF=PEA+∠OEF,∠GFE=PFC+∠OFE,
∴∠GEF+∠GFE=PEA+∠OEF+PFC+∠OFE,
∵由(2)知∠PFC=∠PEA+∠P,
∴∠PEA=∠PFC﹣α,
∵∠OFE+∠OEF=180°﹣∠FOE=180°﹣∠PFC,
∴∠GEF+∠GFE=(∠PFC﹣α)+∠PFC+180°﹣∠PFC=180°﹣α,
∴∠G=180°﹣(∠GEF+∠GFE)=180°﹣180°+α=α.
故答案为:α.
24.解:(1)∵OF⊥AB,
∴∠BOF=∠AOF=90°
∵OE平分∠AOC,
∴∠AOE=∠COE=∠AOC,
又∵∠AOC=∠BOD,∠COE+∠BOD=57°.
∴∠AOE=∠COE=×57°=19°,
∴∠AOC=∠BOD=38°,
∴∠DOF=∠BOD+∠BOF=38°+90°=128°,
(2)由对顶角相等可得∠AOC=∠BOD,∠AOD=∠BOC,
由角平分线的定义可得∠AOE=∠COE,
∵∠BOE+∠AOE=180°=∠DOE+∠COE,
而∠AOE=∠COE,
∴∠BOE=∠DOE,
故图中相等的角有∠AOE=∠COE,∠AOC=∠BOD,∠AOD=∠∠BOC,∠BOE=∠DOE.
25.解:(1)设乙种商品每件的进价是x元,则甲种商品每件的进价是(x+20)元,依题意有
4(x+20)=5x,
解得x=80,
则x+20=80+20=100.
故甲种商品每件的进价是100元,乙种商品每件的进价是80元;
(2)设该商场从厂家购进了甲种商品y件,则乙种商品(50﹣y)件,依题意有
100y+80(50﹣y)=4600,
解得y=30,
则50﹣y=50﹣30=20,
则100×40%×30+30×20=1800(元).
故全部售出后共可获利1800元;
(3)设乙商品按标价售出z件,则乙商品按促销价售出(20﹣z)件,依题意有
(100+100×40%)×0.9×30+(80+30)z+[(80+30)×0.9﹣4](20﹣z)=4600+1800×(1﹣),
解得z=8.
故乙商品按标价售出8件.
26.解:(1)20×2+(25﹣20)×2.5+0.3×25=60(元),
答:他应缴水费60元.
(2)∵20×2+0.3×20=46>41.4,
故水表有故障时,计入用水量不超过20吨,
设该用户12月份实际用水x吨,
由题意,得2×60%x+0.3×60%x=41.4,
解得x=30,
答:该用户12月份实际用水30吨.
27.证明:(1)∵AB∥CD,
∴∠AFE=∠FED,
∵∠AGH=∠FED,
∴∠AFE=∠AGH,
∴EF∥GH,
∴∠FEH+∠H=180°,
∵FE⊥HE,
∴∠FEH=90°,
∴∠H=180°﹣∠FEH=90°,
∴HG⊥HE;
(2)过点M作MQ∥AB,
∵AB∥CD,
∴MQ∥CD,
过点H作HP∥AB,
∵AB∥CD,
∴HP∥CD,
∵GM平分∠HGB,
∴∠BGM=∠HGM=∠BGH,
∵EM平分∠HED,
∴∠HEM=∠DEM=∠HED,
∵MQ∥AB,
∴∠BGM=∠GMQ,
∵MQ∥CD,
∴∠QME=∠MED,
∴∠GME=∠GMQ+∠QME=∠BGM+∠MED,
∵HP∥AB,
∴∠BGH=∠GHP=2∠BGM,
∵HP∥CD,
∴∠PHE=∠HED=2∠MED,
∴∠GHE=∠GHP+∠PHE=2∠BGM+2∠MED=2(∠BGM+∠MED),
∴∠GHE=∠2GME;
(3)过点M作MQ∥AB,过点H作HP∥AB,
由∠KFE:∠MGH=13:5,设∠KFE=13x,∠MGH=5x,
由(2)可知:∠BGH=2∠MGH=10x,
∵∠AFE+∠BFE=180°,
∴∠AFE=180°﹣10x,
∵FK平分∠AFE,
∴∠AFK=∠KFE=∠AFE,
即,
解得:x=5°,
∴∠BGH=10x=50°,
∵HP∥AB,HP∥CD,
∴∠BGH=∠GHP=50°,∠PHE=∠HED,
∵∠GHE=90°,
∴∠PHE=∠GHE﹣∠GHP=90°﹣50°=40°,
∴∠HED=40°.
同课章节目录
