2.1.1-2.1.3平面向量的实际背景及基本概念题组训练-2021-2022学年高一上学期数学人教A版必修4(Word含答案解析)
文档属性
| 名称 | 2.1.1-2.1.3平面向量的实际背景及基本概念题组训练-2021-2022学年高一上学期数学人教A版必修4(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 129.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 18:07:58 | ||
图片预览



文档简介
第二章 平面向量
2.1 平面向量的实际背景及基本概念
2.1.1 向量的物理背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与共线向量
基础过关练
题组一 向量的物理背景与概念
1.下列物理量:①质量;②速度;③位移;④力;⑤加速度;⑥路程.其中是向量(矢量)的有( )
A.2个 B.3个 C.4个 D.5个
题组二 向量的几何表示
2.如图,在☉O中,向量,,是( )
A.有相同起点的向量 B.共线向量 C.模相等的向量 D.相等向量
3.以下说法正确的是( )
A.零向量没有方向 B.单位向量都相等
C.共线向量又叫平行向量 D.任何向量的模都是正实数
4.已知A={与a共线的向量},B={与a长度相等的向量},C={与a长度相等,方向相反的向量},其中a为非零向量,则下列说法中错误的是( )
A.C A B.A∩B={a} C.C B D.{a} A∩B
5.若||=||,且=,则四边形ABCD的形状为( )
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
6.(浙江高一期中)设点O是正方形ABCD的中心,则下列结论错误的是( )
A.= B.∥ C.与共线 D.=
7.设数轴上有四个点A,B,C,D,其中A,C对应的实数分别是1和-3,且=,是单位向量,则点B对应的实数为 ;点D对应的实数为 ;||= .
8.一架飞机从A点向西北方向飞行200 km到达B点,再从B点向正东方向飞行100 km到达C点,求飞机从C点飞回A点的位移.
题组三 相等向量与共线向量
9.下列说法中不正确的是( )
A.方向相同或相反的非零向量叫做平行向量
B.长度相等且方向相同的向量叫做相等向量
C.有公共起点的向量叫做共线向量
D.零向量与任一向量共线
10.下列说法中正确的是( )
A.向量∥是指所在的直线平行于所在的直线
B.共线向量是指在同一条直线上的向量
C.长度相等的向量叫做相等向量
D.零向量长度等于0
11.若a∥b,b∥c,则a∥c( )
A.总成立 B.当a≠0时成立 C.当b≠0时成立 D.当c≠0时成立
12.正n边形有n条边,它们对应的向量依次为a1,a2,a3,…,an,则这n个向量( )
A.都相等 B.都共线 C.都不共线 D.模都相等
13.如图,半圆的直径AB=6,C是半圆上的一点,D,E分别是AB,BC上的点,且AD=1,BE=4,DE=3.
(1)求证:∥;
(2)求||.
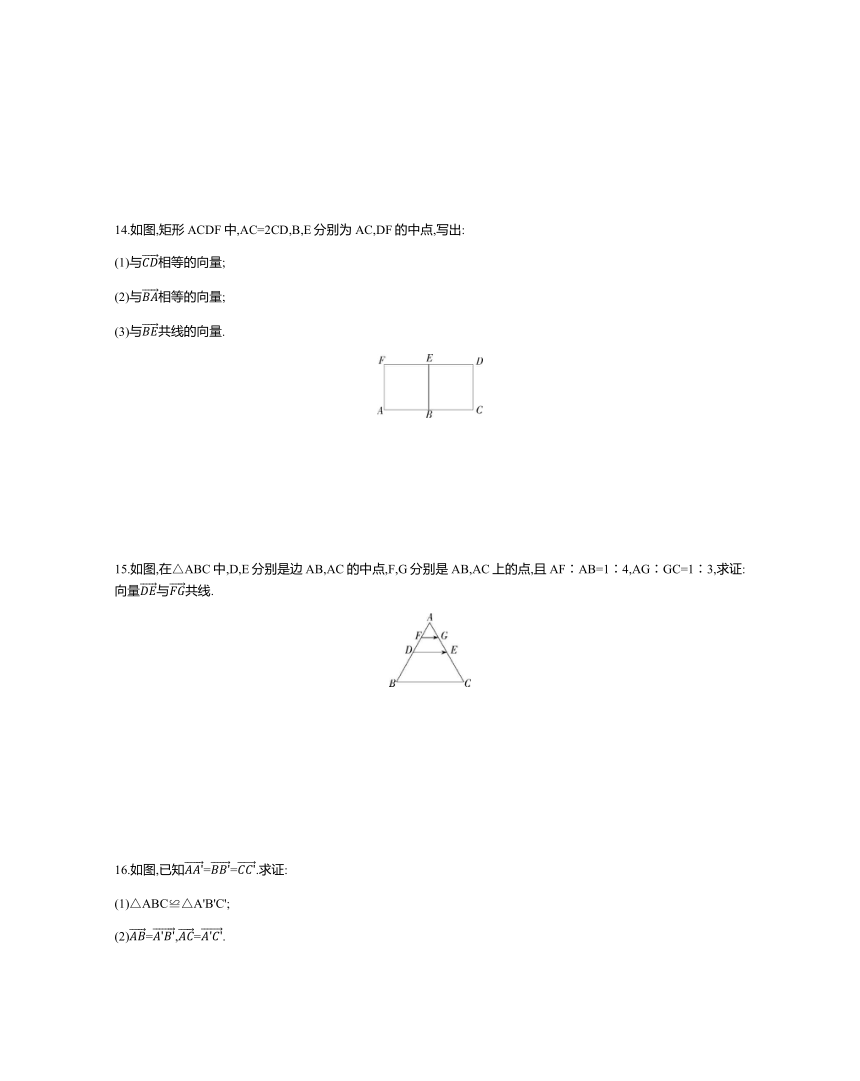
14.如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:
(1)与相等的向量;
(2)与相等的向量;
(3)与共线的向量.
15.如图,在△ABC中,D,E分别是边AB,AC的中点,F,G分别是AB,AC上的点,且AF∶AB=1∶4,AG∶GC=1∶3,求证:向量与共线.
16.如图,已知==.求证:
(1)△ABC≌△A'B'C';
(2)=,=.
能力提升练
一、选择题
1.(北京四中月考,★★☆)下列说法中正确的是( )
A.若两个向量相等,则它们的起点和终点分别重合 B.模相等的两个平行向量是相等向量
C.若a和b都是单位向量,则a=b D.两个相等向量的模相等
2.(重庆铜梁一中高一月考,★★☆)设e1,e2是两个单位向量,则下列结论中正确的是( )
A.e1=e2 B.e1∥e2 C.e1=-e2 D.|e1|=|e2|
3.(河北石家庄辛集中学高一下期中,★★☆)下列命题正确的是( )
A.向量与是相等向量 B.若a,b都是单位向量,则|a|=|b|
C.若=,则A,B,C,D四点构成平行四边形 D.若两向量相等,则它们的起点、终点相同
4.(★★☆)某人向正东方向行进100 m后,再向正南方向行进100 m,则此人位移的方向是( )
A.南偏东60° B.南偏东45° C.南偏东30° D.南偏东15°
二、填空题
5.(★★☆)给出下列几种说法:
①若|a|=|b|,则a=b;
②向量的模一定是正数;
③起点不同,但方向相同且模相等的向量是相等向量.
其中说法正确的是 .(填序号)
三、解答题
6.(★★☆)如图是中国象棋的半个棋盘,“马走日”是象棋中“马”的走法,例如“马”可以从A跳到A1,也可以跳到A2,现用向量,表示“马”走了“一步”,试在图中画出“马”分别从B,C处走了“一步”的所有情况.
7.(★★☆)如图所示,4×3的网格中(每个小方格都是单位正方形),在起点和终点都在小方格的顶点处的向量中,试问:
(1)与向量相等的向量共有几个
(2)与向量平行且模为的向量共有几个
(3)与向量方向相同且模为3的向量共有几个
8.(★★★)如图所示,四边形ABCD中,=,N,M分别是AD,BC上的点,且=.
求证:=.
答案全解全析
第二章 平面向量
2.1 平面向量的实际背景及基本概念
2.1.1 向量的物理
背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与
共线向量
基础过关练
1.C 向量是既有大小又有方向的量,故②③④⑤是向量.质量和路程都只有大小,没有方向,故不是向量.所以是向量的有4个.
2.C 易知||=||=||=圆的半径,故选C.
3.C 规定零向量的方向是任意的,故A错误;单位向量的模相等,都是1,但方向不同,故B错误;共线向量就是平行向量,故C正确;零向量的模等于0,故D错误.
4.B A∩B中有a的相反向量,所以B错误.
5.C 由=可知四边形ABCD为平行四边形.又由||=||可知平行四边形ABCD为菱形.
6.D 如图,∵与方向相同,长度相等,∴=,A正确;∵B,O,D三点在一条直线上,∴∥,B正确;∵AB∥CD,∴与共线,C正确;∵与方向不同,∴≠,D错误.故选D.
7.答案 -7;-4或-2;4
解析 记B,D对应的实数分别是b,d.
由=可得点B在点C的左侧且||=||,则1-(-3)=-3-b,解得b=-7,即点B对应的实数为-7.由是单位向量可得||=1,则|-3-d|=1,解得d=-4或d=-2.||=|(-3)-(-7)|=4.
8.解析 如图所示,由题意得C点在A点的正北方向,且||=100 km,故飞机从C点飞回A点的位移的方向为正南方向,长度为100 km.
9.C 有公共起点的向量方向不一定相同或相反,故不一定共线.
10.D 向量∥是指所在的直线平行或重合于所在的直线,故A错误;共线向量所在的直线可能重合,也可能平行,故B错误;方向相同且长度相等的向量叫做相等向量,故C错误;长度为0的向量叫做零向量,记作0,故D正确.故选D.
11.C 由于0与任一向量平行,所以当b≠0时,有“a∥b,b∥c,则a∥c”成立.
12.D 正n边形的n条边长都相等,所以这n个向量的模都相等.
13.解析 (1)证明:由题意知,在△DBE中,BD=5,DE=3,BE=4,∴△DBE是直角三角形,∠DEB=90°.
又∵点C为半圆上一点,∴∠ACB=90°.
∴AC∥DE,∴∥.
(2)易知△ABC∽△DBE,
∴=,即=,
∴AC=,即||=.
14.解析 在矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,所以四边形ABEF与四边形BCDE均为正方形.
(1)与相等的向量有,.
(2)与相等的向量有,,.
(3)与共线的向量有,,,,.
15.证明 ∵D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,∴DE∥BC①.
∵AF∶AB=1∶4,∴AF∶FB=1∶3,
又AG∶GC=1∶3,∴AF∶FB=AG∶GC,∴FG∥BC②.
由①②可知,DE∥FG,故向量与共线.
16.证明 (1)∵=,∴||=||,且∥,∴AA' BB'.
∴四边形AA'B'B是平行四边形,∴||=||.同理||=||,||=||.∴△ABC≌△A'B'C'.
(2)由(1)知||=||,∥,且与的方向相同,∴=.
由(1)知||=||,∥,且与的方向相同,∴=.
能力提升练
一、选择题
1.D 向量是可以平移的,若两个向量相等,则它们的起点和终点不一定分别重合,A说法错误;向量相等要满足模相等,且方向相同,模相等的两个平行向量的方向不一定相同,B说法错误;a和b都是单位向量,但两向量的方向不一定相同,故a=b不一定成立,C说法错误;两个相等向量的模一定相等,D说法正确.故选D.
2.D 单位向量即模为1的向量.若e1,e2是两个单位向量,则|e1|=|e2|=1.故选D.
3.B A选项,因为向量与长度相等,方向相反,所以向量与是平行向量,不是相等相量,故A错误;B选项,单位向量是模为1的向量,故|a|和|b|一定相等,故B正确;C选项,若=,则和可能在一条直线上,故C错误;D选项,两向量相等只需要方向相同,模相等就可以,跟起点、终点没有关系,故D错误.
4.C 如图所示,设此人从点A出发,经由点B,到达点C,则tan∠BAC==,
∴∠BAC=60°,故位移的方向是东偏南60°,即南偏东30°.故选C.
二、填空题
5.答案 ③
解析 ①错误.|a|=|b|仅能说明a与b的模相等,不能说明它们方向的关系,故a=b不一定成立.
②错误.零向量的模为0.
③正确.向量仅由它的大小和方向确定,与起点的位置无关.
三、解答题
6.解析 利用“马走日”画出“马”分别在B,C处走了“一步”的所有情况.作出符合要求的所有向量,如图.
7.解析 (1)根据相等向量的概念,可得与向量相等的向量共有5个(不包括本身).
(2)根据向量的模的概念,可得与向量平行且模为的向量共有24个.
(3)根据向量的模的概念,可得与向量方向相同且模为3的向量共有2个.
8.证明 ∵=,∴||=||且∥,∴四边形ABCD是平行四边形,
∴||=||,且∥.
又∵与的方向相同,∴=.
易证四边形CNAM是平行四边形,
∴=,∴||=||.
又∵||=||,∴||=||,
又∵与的方向相同,∴=.
2.1 平面向量的实际背景及基本概念
2.1.1 向量的物理背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与共线向量
基础过关练
题组一 向量的物理背景与概念
1.下列物理量:①质量;②速度;③位移;④力;⑤加速度;⑥路程.其中是向量(矢量)的有( )
A.2个 B.3个 C.4个 D.5个
题组二 向量的几何表示
2.如图,在☉O中,向量,,是( )
A.有相同起点的向量 B.共线向量 C.模相等的向量 D.相等向量
3.以下说法正确的是( )
A.零向量没有方向 B.单位向量都相等
C.共线向量又叫平行向量 D.任何向量的模都是正实数
4.已知A={与a共线的向量},B={与a长度相等的向量},C={与a长度相等,方向相反的向量},其中a为非零向量,则下列说法中错误的是( )
A.C A B.A∩B={a} C.C B D.{a} A∩B
5.若||=||,且=,则四边形ABCD的形状为( )
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
6.(浙江高一期中)设点O是正方形ABCD的中心,则下列结论错误的是( )
A.= B.∥ C.与共线 D.=
7.设数轴上有四个点A,B,C,D,其中A,C对应的实数分别是1和-3,且=,是单位向量,则点B对应的实数为 ;点D对应的实数为 ;||= .
8.一架飞机从A点向西北方向飞行200 km到达B点,再从B点向正东方向飞行100 km到达C点,求飞机从C点飞回A点的位移.
题组三 相等向量与共线向量
9.下列说法中不正确的是( )
A.方向相同或相反的非零向量叫做平行向量
B.长度相等且方向相同的向量叫做相等向量
C.有公共起点的向量叫做共线向量
D.零向量与任一向量共线
10.下列说法中正确的是( )
A.向量∥是指所在的直线平行于所在的直线
B.共线向量是指在同一条直线上的向量
C.长度相等的向量叫做相等向量
D.零向量长度等于0
11.若a∥b,b∥c,则a∥c( )
A.总成立 B.当a≠0时成立 C.当b≠0时成立 D.当c≠0时成立
12.正n边形有n条边,它们对应的向量依次为a1,a2,a3,…,an,则这n个向量( )
A.都相等 B.都共线 C.都不共线 D.模都相等
13.如图,半圆的直径AB=6,C是半圆上的一点,D,E分别是AB,BC上的点,且AD=1,BE=4,DE=3.
(1)求证:∥;
(2)求||.
14.如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:
(1)与相等的向量;
(2)与相等的向量;
(3)与共线的向量.
15.如图,在△ABC中,D,E分别是边AB,AC的中点,F,G分别是AB,AC上的点,且AF∶AB=1∶4,AG∶GC=1∶3,求证:向量与共线.
16.如图,已知==.求证:
(1)△ABC≌△A'B'C';
(2)=,=.
能力提升练
一、选择题
1.(北京四中月考,★★☆)下列说法中正确的是( )
A.若两个向量相等,则它们的起点和终点分别重合 B.模相等的两个平行向量是相等向量
C.若a和b都是单位向量,则a=b D.两个相等向量的模相等
2.(重庆铜梁一中高一月考,★★☆)设e1,e2是两个单位向量,则下列结论中正确的是( )
A.e1=e2 B.e1∥e2 C.e1=-e2 D.|e1|=|e2|
3.(河北石家庄辛集中学高一下期中,★★☆)下列命题正确的是( )
A.向量与是相等向量 B.若a,b都是单位向量,则|a|=|b|
C.若=,则A,B,C,D四点构成平行四边形 D.若两向量相等,则它们的起点、终点相同
4.(★★☆)某人向正东方向行进100 m后,再向正南方向行进100 m,则此人位移的方向是( )
A.南偏东60° B.南偏东45° C.南偏东30° D.南偏东15°
二、填空题
5.(★★☆)给出下列几种说法:
①若|a|=|b|,则a=b;
②向量的模一定是正数;
③起点不同,但方向相同且模相等的向量是相等向量.
其中说法正确的是 .(填序号)
三、解答题
6.(★★☆)如图是中国象棋的半个棋盘,“马走日”是象棋中“马”的走法,例如“马”可以从A跳到A1,也可以跳到A2,现用向量,表示“马”走了“一步”,试在图中画出“马”分别从B,C处走了“一步”的所有情况.
7.(★★☆)如图所示,4×3的网格中(每个小方格都是单位正方形),在起点和终点都在小方格的顶点处的向量中,试问:
(1)与向量相等的向量共有几个
(2)与向量平行且模为的向量共有几个
(3)与向量方向相同且模为3的向量共有几个
8.(★★★)如图所示,四边形ABCD中,=,N,M分别是AD,BC上的点,且=.
求证:=.
答案全解全析
第二章 平面向量
2.1 平面向量的实际背景及基本概念
2.1.1 向量的物理
背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与
共线向量
基础过关练
1.C 向量是既有大小又有方向的量,故②③④⑤是向量.质量和路程都只有大小,没有方向,故不是向量.所以是向量的有4个.
2.C 易知||=||=||=圆的半径,故选C.
3.C 规定零向量的方向是任意的,故A错误;单位向量的模相等,都是1,但方向不同,故B错误;共线向量就是平行向量,故C正确;零向量的模等于0,故D错误.
4.B A∩B中有a的相反向量,所以B错误.
5.C 由=可知四边形ABCD为平行四边形.又由||=||可知平行四边形ABCD为菱形.
6.D 如图,∵与方向相同,长度相等,∴=,A正确;∵B,O,D三点在一条直线上,∴∥,B正确;∵AB∥CD,∴与共线,C正确;∵与方向不同,∴≠,D错误.故选D.
7.答案 -7;-4或-2;4
解析 记B,D对应的实数分别是b,d.
由=可得点B在点C的左侧且||=||,则1-(-3)=-3-b,解得b=-7,即点B对应的实数为-7.由是单位向量可得||=1,则|-3-d|=1,解得d=-4或d=-2.||=|(-3)-(-7)|=4.
8.解析 如图所示,由题意得C点在A点的正北方向,且||=100 km,故飞机从C点飞回A点的位移的方向为正南方向,长度为100 km.
9.C 有公共起点的向量方向不一定相同或相反,故不一定共线.
10.D 向量∥是指所在的直线平行或重合于所在的直线,故A错误;共线向量所在的直线可能重合,也可能平行,故B错误;方向相同且长度相等的向量叫做相等向量,故C错误;长度为0的向量叫做零向量,记作0,故D正确.故选D.
11.C 由于0与任一向量平行,所以当b≠0时,有“a∥b,b∥c,则a∥c”成立.
12.D 正n边形的n条边长都相等,所以这n个向量的模都相等.
13.解析 (1)证明:由题意知,在△DBE中,BD=5,DE=3,BE=4,∴△DBE是直角三角形,∠DEB=90°.
又∵点C为半圆上一点,∴∠ACB=90°.
∴AC∥DE,∴∥.
(2)易知△ABC∽△DBE,
∴=,即=,
∴AC=,即||=.
14.解析 在矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,所以四边形ABEF与四边形BCDE均为正方形.
(1)与相等的向量有,.
(2)与相等的向量有,,.
(3)与共线的向量有,,,,.
15.证明 ∵D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,∴DE∥BC①.
∵AF∶AB=1∶4,∴AF∶FB=1∶3,
又AG∶GC=1∶3,∴AF∶FB=AG∶GC,∴FG∥BC②.
由①②可知,DE∥FG,故向量与共线.
16.证明 (1)∵=,∴||=||,且∥,∴AA' BB'.
∴四边形AA'B'B是平行四边形,∴||=||.同理||=||,||=||.∴△ABC≌△A'B'C'.
(2)由(1)知||=||,∥,且与的方向相同,∴=.
由(1)知||=||,∥,且与的方向相同,∴=.
能力提升练
一、选择题
1.D 向量是可以平移的,若两个向量相等,则它们的起点和终点不一定分别重合,A说法错误;向量相等要满足模相等,且方向相同,模相等的两个平行向量的方向不一定相同,B说法错误;a和b都是单位向量,但两向量的方向不一定相同,故a=b不一定成立,C说法错误;两个相等向量的模一定相等,D说法正确.故选D.
2.D 单位向量即模为1的向量.若e1,e2是两个单位向量,则|e1|=|e2|=1.故选D.
3.B A选项,因为向量与长度相等,方向相反,所以向量与是平行向量,不是相等相量,故A错误;B选项,单位向量是模为1的向量,故|a|和|b|一定相等,故B正确;C选项,若=,则和可能在一条直线上,故C错误;D选项,两向量相等只需要方向相同,模相等就可以,跟起点、终点没有关系,故D错误.
4.C 如图所示,设此人从点A出发,经由点B,到达点C,则tan∠BAC==,
∴∠BAC=60°,故位移的方向是东偏南60°,即南偏东30°.故选C.
二、填空题
5.答案 ③
解析 ①错误.|a|=|b|仅能说明a与b的模相等,不能说明它们方向的关系,故a=b不一定成立.
②错误.零向量的模为0.
③正确.向量仅由它的大小和方向确定,与起点的位置无关.
三、解答题
6.解析 利用“马走日”画出“马”分别在B,C处走了“一步”的所有情况.作出符合要求的所有向量,如图.
7.解析 (1)根据相等向量的概念,可得与向量相等的向量共有5个(不包括本身).
(2)根据向量的模的概念,可得与向量平行且模为的向量共有24个.
(3)根据向量的模的概念,可得与向量方向相同且模为3的向量共有2个.
8.证明 ∵=,∴||=||且∥,∴四边形ABCD是平行四边形,
∴||=||,且∥.
又∵与的方向相同,∴=.
易证四边形CNAM是平行四边形,
∴=,∴||=||.
又∵||=||,∴||=||,
又∵与的方向相同,∴=.
