2021-2022学年北师大版九年级数学下册1.5三角函数的应用同步测试(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.5三角函数的应用同步测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 271.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 08:21:26 | ||
图片预览




文档简介
北师大版九年级数学下册第一章1.5三角函数的应用 同步测试
一.选择题
1.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.米 B.4sinα米 C.米 D.4cosα米
2.如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 B. C. D.
3.如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
A.250米 B.250 米 C. 米 D.500 米
4.如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A.100米 B.50米 C.米 D.50米
5.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A,B的距离,他们设计了如图的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中4位同学分别测得四组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB;④∠F,∠ADB,FB.其中能根据所测数据求得A,B两树距离的有( )
A.1组 B.2组 C.3组 D.4组
6.某屋顶示意图如图所示,现要在屋顶上开一个天窗,天窗AB在水平位置,屋顶坡面长度PQ=QD=4.8米,则屋顶水平跨度PD的长为( )米
A.cosα B.cosα C.sinα D.sinα
7. 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
A.5cm B.5cm C.10m D.m
8.如图钓鱼竿AC长6m,露在水面上的鱼线BC长3m,钓者想看看鱼钓上的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )
A.3m B.m C.m D.4m
9.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为( )
A.26米 B.28米 C.30米 D.46米
10.如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
A.0.55 B.0.8 C.0.6 D.0.75
11.如图所示,某地修建高速公路,要从B地向C地修一条隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100 m到达A处,在A处观察B地的俯角为30°,则B,C两地之间的距离为( )
A.100 m B.50 m C.50 m D. m
12.某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角45°的传送带AB,调整为坡度i=1:的新传送带AC(如图所示).已知原传送带AB的长是4米,那么新传送带AC的长是( )
A.8米 B.4米 C.6米 D.3米
二.填空题
13.如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了_____________米.
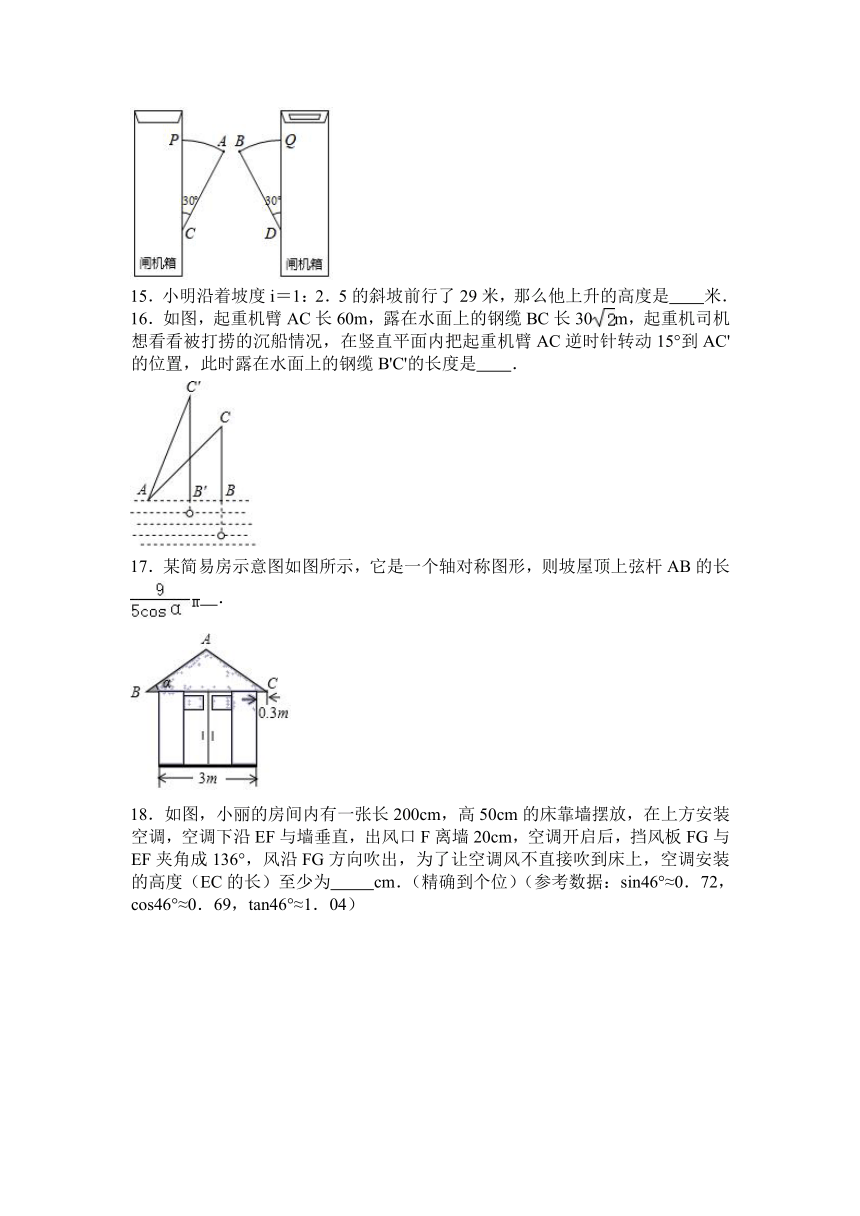
14.如图是一个地铁站入口的双翼闸机.它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为 64 cm.
15.小明沿着坡度i=1:2.5的斜坡前行了29米,那么他上升的高度是 米.
16.如图,起重机臂AC长60m,露在水面上的钢缆BC长30m,起重机司机想看看被打捞的沉船情况,在竖直平面内把起重机臂AC逆时针转动15°到AC'的位置,此时露在水面上的钢缆B'C'的长度是 .
17.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长 .
18.如图,小丽的房间内有一张长200cm,高50cm的床靠墙摆放,在上方安装空调,空调下沿EF与墙垂直,出风口F离墙20cm,空调开启后,挡风板FG与EF夹角成136°,风沿FG方向吹出,为了让空调风不直接吹到床上,空调安装的高度(EC的长)至少为 cm.(精确到个位)(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
19.如图所示,一水库迎水坡AB的坡度i=1:2,求坡角α的正弦值sinα
20.如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?
21.如图1,这是阳台电动升降晾衣架,它左侧的基本形状是菱形,通过调节菱形内角的大小,从而实现升降晾衣杆.图2是晾衣架左侧的示意图,已知菱形的边长为15cm当晾衣架伸展至长(即点O到直线 l2的距离)为105cm时,求∠OAP的大小.(参考数据:sin15°≈0.26,cos15°≈0.97,sin51.3°≈0.78,sin58.1°≈0.85)
22. 如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=6 米,背水坡CD的坡度i=1∶(i为DF与FC的比值),则背水坡的坡长多少米?
23.滨河公园的健身器材中有种不等臂(即AC≠CB)的跷跷板,跷跷板AB长为2.9米,为了缓冲一端下落时对人的冲击力,在两端的下方分别固定一支柱作为支撑(即AE、BF).如图,已知两端分别着地时离地面的高度为:AE=0.24米,BF=0.32米;与水平线的夹角分别为α=14°,β=18.8°;求支柱CD的长.(结果精确到0.1米,参考数值:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,sin18.8°≈0.32,cos18.8°≈0.95,tan18.8°≈0.34)
24.某公园有一座古塔,古塔前有一个斜坡CD,坡角∠DCE=42°,斜坡高DE=1.8米,DQ是平行于水平地面BC的一个平台.小华想利用所学知识测量古塔的高度AB,她在平台的点G处水平放置一平面镜,并沿着DG方向移动,当移动到点N时,刚好在镜面中看到古塔顶端点A的像,这时,测得小华眼睛与地面的距离MN=1.5米,GN=2米,BC=16米,DG=8米,已知AB⊥BC,MN⊥DQ,请你根据题中提供的相关信息,求出古塔的高度AB.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
25.如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长?(参考数据:≈1.7,结果保留一位小数)
答案提示
1.B.2.C.3.A.4.B.5.C.①②③6.B.7.C.8.B.9.D.10.D.11.A.12.A.
13.1000.14.64.15.2.16.30.17..18.223.
19.解:过A作AC⊥BC于C,
∵AB的坡度i=1:3,
∴tanα=
设AC=x,BC=3x,
根据勾股定理可得:AB=
则sinα=AC 故答案为:
20.解:过点A作AC⊥BD于点C,则AC的长是点A到BD的最短距离.
依题意知∠CAD=30°,∠CAB=60°,
∴∠BAD=60°-30°=30°,∠ABD=90°-60°=30°,
∴∠ABD=∠BAD,∴AD=BD=12海里.
∵∠CAD=30°,∠ACD=90°,
∴CD=AD=6海里,
由勾股定理得AC==6 (海里)>8海里,
故渔船没有触礁的危险
21.解:如图,连接AB,OP交于M,
∵四边形APBO是菱形,
∴AB⊥OP,∠OAP=2∠OAB,
由题意得,OM==,AO=15,
∴sin∠OAB==≈0.78,
∴∠OAB=51.3°,
∴∠OAP=2∠OAB=102.6°.
22.解: 如图,在Rt△DCE中,
∵cos∠EDC=,
∴DC=DE·cos∠EDC=1.8×cos15°≈1.746(m).
在Rt△ABC中,∠BAC=90°-75°=15°.
∵sin∠BAC=,
∴BC=AB·sin∠BAC=1.8×sin15°≈0.468(m).
∴BD=DC-BC≈1.28 m.
23.解:过点A作AM⊥CD于点M,过点B作BG⊥CD于点G,则四边形AEDM、BFDG为矩形,
由题意知AE=0.24米,BF=0.32米,AB=2.9米,
∠CAM=14°,∠CBG=18.8°,
∴DM=AE=0.24米,DG=BF=0.32米,
设CD=x,
则CM=x﹣0.24,CG=x﹣0.32,
在Rt△ACM中,∠CAM=14°,
sin∠CAM=,
∴AC=,
在Rt△BCG中,∠CBG=18.8°,
sin∠CBG=,
∴BC=,
∵AB=AC+BC
∴+=2.9
解得:x≈0.7,
即支柱CD的长为0.7米.
24.解:在Rt△CDE中,tan∠DCE=,
∴0.9=,
∴CE=2,
延长GD交AB于点H,则BH=DE=1.8(米),DH=BE=BC+CE=18(米),HG=DH+DG=26(米),
∵∠AHG=∠MNG=90°,∠AGH=∠MGN,
∴△AHG∽△MNG,
∴,
即,
∴AH=19.5(米),
∴AB=AH+HB=21.3(米).
答:古塔的高度AB为21.3米.
25.解:过点B作BE⊥AC于点E,延长DG交CA于点H,得Rt△ABE和矩形BEHG.
i==,
∵BE=8,AE=6,DG=1.5,BG=1,
∴DH=DG+GH=1.5+8=9.5,
AH=AE+EH=6+1=7.
在Rt△CDH中,
∵∠C=∠FDC=30°,DH=9.5,tan30°=,
∴CH=9.5.
又∵CH=CA+7,
即9.5=CA+7,
∴CA≈9.15≈9.2(米).
答:CA的长约是9.2米.
一.选择题
1.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.米 B.4sinα米 C.米 D.4cosα米
2.如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 B. C. D.
3.如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
A.250米 B.250 米 C. 米 D.500 米
4.如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A.100米 B.50米 C.米 D.50米
5.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A,B的距离,他们设计了如图的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中4位同学分别测得四组数据:①AC,∠ACB;②EF,DE,AD;③CD,∠ACB,∠ADB;④∠F,∠ADB,FB.其中能根据所测数据求得A,B两树距离的有( )
A.1组 B.2组 C.3组 D.4组
6.某屋顶示意图如图所示,现要在屋顶上开一个天窗,天窗AB在水平位置,屋顶坡面长度PQ=QD=4.8米,则屋顶水平跨度PD的长为( )米
A.cosα B.cosα C.sinα D.sinα
7. 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
A.5cm B.5cm C.10m D.m
8.如图钓鱼竿AC长6m,露在水面上的鱼线BC长3m,钓者想看看鱼钓上的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )
A.3m B.m C.m D.4m
9.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为( )
A.26米 B.28米 C.30米 D.46米
10.如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
A.0.55 B.0.8 C.0.6 D.0.75
11.如图所示,某地修建高速公路,要从B地向C地修一条隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100 m到达A处,在A处观察B地的俯角为30°,则B,C两地之间的距离为( )
A.100 m B.50 m C.50 m D. m
12.某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角45°的传送带AB,调整为坡度i=1:的新传送带AC(如图所示).已知原传送带AB的长是4米,那么新传送带AC的长是( )
A.8米 B.4米 C.6米 D.3米
二.填空题
13.如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了_____________米.
14.如图是一个地铁站入口的双翼闸机.它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为 64 cm.
15.小明沿着坡度i=1:2.5的斜坡前行了29米,那么他上升的高度是 米.
16.如图,起重机臂AC长60m,露在水面上的钢缆BC长30m,起重机司机想看看被打捞的沉船情况,在竖直平面内把起重机臂AC逆时针转动15°到AC'的位置,此时露在水面上的钢缆B'C'的长度是 .
17.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长 .
18.如图,小丽的房间内有一张长200cm,高50cm的床靠墙摆放,在上方安装空调,空调下沿EF与墙垂直,出风口F离墙20cm,空调开启后,挡风板FG与EF夹角成136°,风沿FG方向吹出,为了让空调风不直接吹到床上,空调安装的高度(EC的长)至少为 cm.(精确到个位)(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
19.如图所示,一水库迎水坡AB的坡度i=1:2,求坡角α的正弦值sinα
20.如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?
21.如图1,这是阳台电动升降晾衣架,它左侧的基本形状是菱形,通过调节菱形内角的大小,从而实现升降晾衣杆.图2是晾衣架左侧的示意图,已知菱形的边长为15cm当晾衣架伸展至长(即点O到直线 l2的距离)为105cm时,求∠OAP的大小.(参考数据:sin15°≈0.26,cos15°≈0.97,sin51.3°≈0.78,sin58.1°≈0.85)
22. 如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=6 米,背水坡CD的坡度i=1∶(i为DF与FC的比值),则背水坡的坡长多少米?
23.滨河公园的健身器材中有种不等臂(即AC≠CB)的跷跷板,跷跷板AB长为2.9米,为了缓冲一端下落时对人的冲击力,在两端的下方分别固定一支柱作为支撑(即AE、BF).如图,已知两端分别着地时离地面的高度为:AE=0.24米,BF=0.32米;与水平线的夹角分别为α=14°,β=18.8°;求支柱CD的长.(结果精确到0.1米,参考数值:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,sin18.8°≈0.32,cos18.8°≈0.95,tan18.8°≈0.34)
24.某公园有一座古塔,古塔前有一个斜坡CD,坡角∠DCE=42°,斜坡高DE=1.8米,DQ是平行于水平地面BC的一个平台.小华想利用所学知识测量古塔的高度AB,她在平台的点G处水平放置一平面镜,并沿着DG方向移动,当移动到点N时,刚好在镜面中看到古塔顶端点A的像,这时,测得小华眼睛与地面的距离MN=1.5米,GN=2米,BC=16米,DG=8米,已知AB⊥BC,MN⊥DQ,请你根据题中提供的相关信息,求出古塔的高度AB.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
25.如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长?(参考数据:≈1.7,结果保留一位小数)
答案提示
1.B.2.C.3.A.4.B.5.C.①②③6.B.7.C.8.B.9.D.10.D.11.A.12.A.
13.1000.14.64.15.2.16.30.17..18.223.
19.解:过A作AC⊥BC于C,
∵AB的坡度i=1:3,
∴tanα=
设AC=x,BC=3x,
根据勾股定理可得:AB=
则sinα=AC 故答案为:
20.解:过点A作AC⊥BD于点C,则AC的长是点A到BD的最短距离.
依题意知∠CAD=30°,∠CAB=60°,
∴∠BAD=60°-30°=30°,∠ABD=90°-60°=30°,
∴∠ABD=∠BAD,∴AD=BD=12海里.
∵∠CAD=30°,∠ACD=90°,
∴CD=AD=6海里,
由勾股定理得AC==6 (海里)>8海里,
故渔船没有触礁的危险
21.解:如图,连接AB,OP交于M,
∵四边形APBO是菱形,
∴AB⊥OP,∠OAP=2∠OAB,
由题意得,OM==,AO=15,
∴sin∠OAB==≈0.78,
∴∠OAB=51.3°,
∴∠OAP=2∠OAB=102.6°.
22.解: 如图,在Rt△DCE中,
∵cos∠EDC=,
∴DC=DE·cos∠EDC=1.8×cos15°≈1.746(m).
在Rt△ABC中,∠BAC=90°-75°=15°.
∵sin∠BAC=,
∴BC=AB·sin∠BAC=1.8×sin15°≈0.468(m).
∴BD=DC-BC≈1.28 m.
23.解:过点A作AM⊥CD于点M,过点B作BG⊥CD于点G,则四边形AEDM、BFDG为矩形,
由题意知AE=0.24米,BF=0.32米,AB=2.9米,
∠CAM=14°,∠CBG=18.8°,
∴DM=AE=0.24米,DG=BF=0.32米,
设CD=x,
则CM=x﹣0.24,CG=x﹣0.32,
在Rt△ACM中,∠CAM=14°,
sin∠CAM=,
∴AC=,
在Rt△BCG中,∠CBG=18.8°,
sin∠CBG=,
∴BC=,
∵AB=AC+BC
∴+=2.9
解得:x≈0.7,
即支柱CD的长为0.7米.
24.解:在Rt△CDE中,tan∠DCE=,
∴0.9=,
∴CE=2,
延长GD交AB于点H,则BH=DE=1.8(米),DH=BE=BC+CE=18(米),HG=DH+DG=26(米),
∵∠AHG=∠MNG=90°,∠AGH=∠MGN,
∴△AHG∽△MNG,
∴,
即,
∴AH=19.5(米),
∴AB=AH+HB=21.3(米).
答:古塔的高度AB为21.3米.
25.解:过点B作BE⊥AC于点E,延长DG交CA于点H,得Rt△ABE和矩形BEHG.
i==,
∵BE=8,AE=6,DG=1.5,BG=1,
∴DH=DG+GH=1.5+8=9.5,
AH=AE+EH=6+1=7.
在Rt△CDH中,
∵∠C=∠FDC=30°,DH=9.5,tan30°=,
∴CH=9.5.
又∵CH=CA+7,
即9.5=CA+7,
∴CA≈9.15≈9.2(米).
答:CA的长约是9.2米.
