2021-2022学年湘教版八年级数学上册2.6 用尺规做三角形 同步测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学上册2.6 用尺规做三角形 同步测试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 517.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 00:00:00 | ||
图片预览


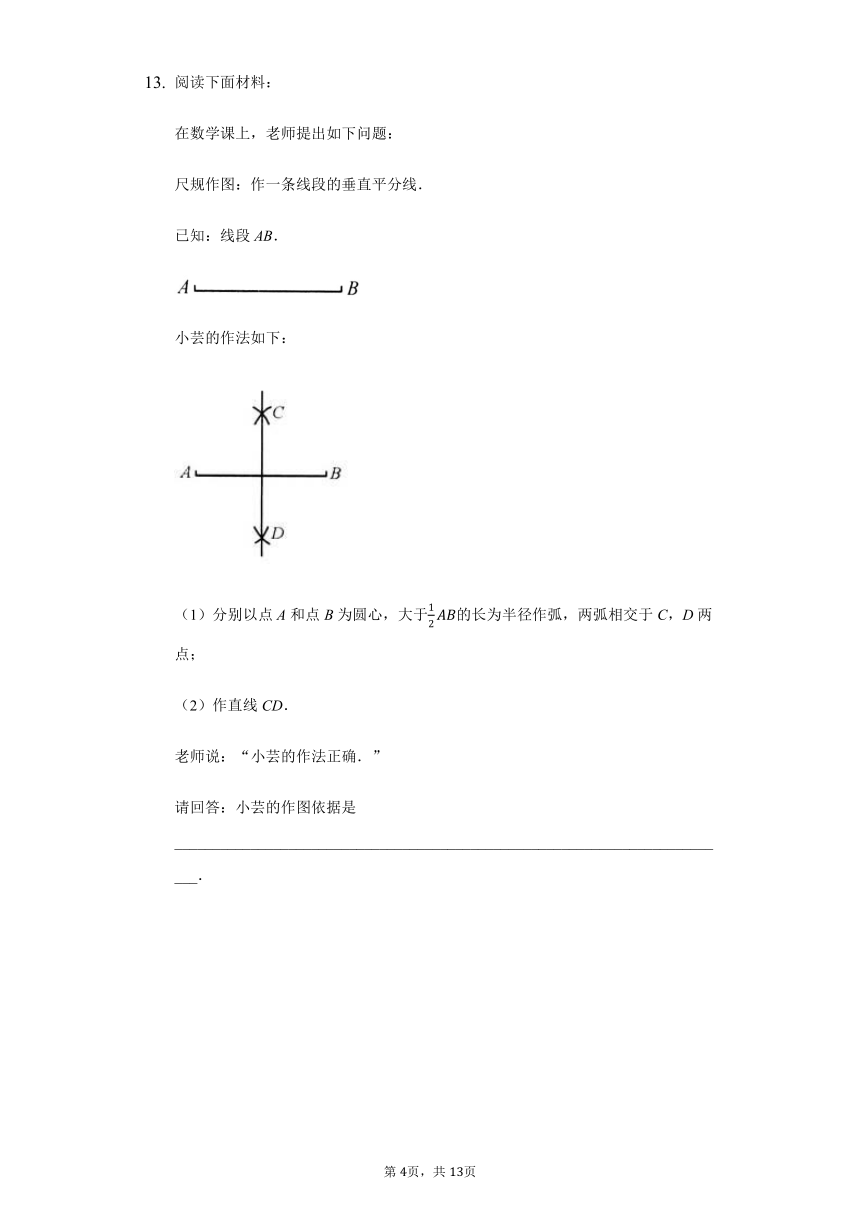

文档简介
2.6 用尺规做三角形同步测试卷 2021-2022学年湘教版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共40分)
给出下列关于三角形的条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角.利用尺规作图,能作出唯一的三角形的条件是()
A. B. C. D.
根据SAS用尺规作三角形,在作图过程中的依据是()
A. 用尺规作一条线段等于已知线段
B. 用尺规作一个角等于已知角
C. 用尺规作一条线段等于已知线段和作一个角等于已知角
D. 不能确定
如图,已知ABC,用尺规作ABC的平分线.如图,步骤如下:
第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在ABC内部交于点P;
第三步:画射线BP,射线BP即为所求.
下列正确的是( )
A. ,均无限制 B. ,的长
C. 有最小限制,无限制 D. ,的长
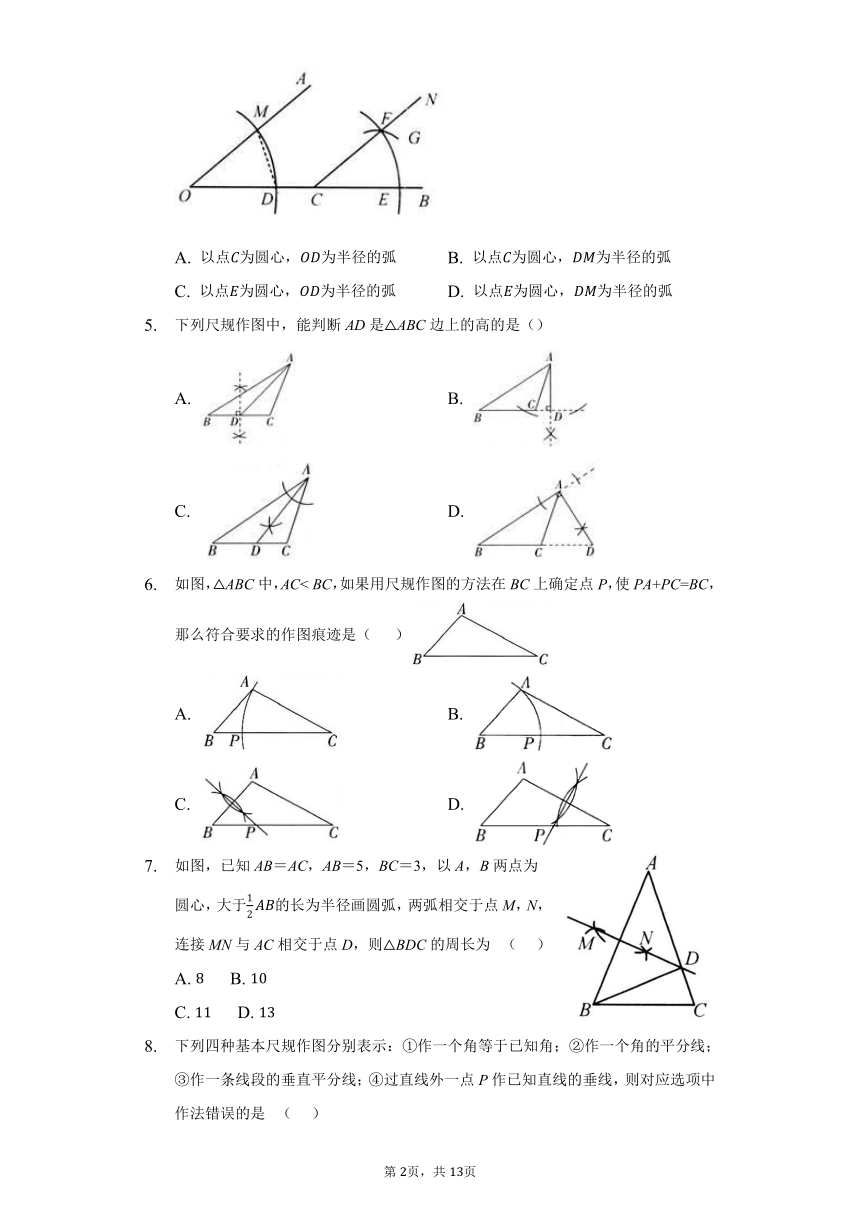
如图,点C在∠AOB的边OB上,用尺规作出了CN // OA,作图痕迹中,弧FG是 ( )
A. 以点为圆心,为半径的弧 B. 以点为圆心,为半径的弧
C. 以点为圆心,为半径的弧 D. 以点为圆心,为半径的弧
下列尺规作图中,能判断AD是△ABC边上的高的是()
A. B.
C. D.
如图,ABC中,AC< BC,如果用尺规作图的方法在BC上确定点P,使PA+PC=BC,那么符合要求的作图痕迹是( )
A. B.
C. D.
如图,已知AB=AC,AB=5,BC=3,以A,B两点为圆心,大于的长为半径画圆弧,两弧相交于点M,N,连接MN与AC相交于点D,则△BDC的周长为 ( )
A. B.
C. D.
下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误的是 ( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下面作法的合理顺序为 .
①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;②作直线BP,在BP上截取BC=a;③连接AB,AC,△ABC为所求作的三角形.
如图,在∠AOB的两边OA,OB上分别截取OM,ON,使OM=ON;再分别以点M,N为圆心,以大于的长为半径作圆弧,两弧交于点E,过点E作EC⊥OA于点C.若EC=2,则点E到直线OB的距离是________.
如图,在RtABC中,B=,以点A为圆心,适当的长为半径画弧,分别交AB、AC于点D、E,再分别以点D、E为圆心,大于DE的长为半径画弧,两弧交于点F,作射线AF交边BC于点G.若BG=1,AC=4,则ACG的面积为 .
如图,在RtABC中,ABC=,根据尺规作图的痕迹判断以下结论:DB=DE;AB=AE;EDC=BAC;DAC=C.其中,错误的是 (填序号).
三、解答题(本大题共8小题,共60分)
阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线.
已知:线段AB.
小芸的作法如下:
(1)分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于C,D两点;
(2)作直线CD.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是__________________________________________________________________________.
如图,已知∠α和∠β,求作∠α+∠β.
请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:∠α,直线l及l上两点A,B.
求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
为进一步打造“宜居城市”,某市拟在新竣工的长方形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图所示.请在原图上利用尺规作图作出音乐喷泉M的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
如图,已知四边形ABCD.求作:点P,使PCB=B,且点P到边AD和CD的距离相等.
角平分线上的点到角的两边的距离相等,到角的两边的距离相等的点在角的平分线上,如图1所示.
(1)若∠BAD=∠CAD,且DB⊥AB于点B,DC⊥AC于点C,则BD=CD;
(2)若DB⊥AB于点B,DC⊥AC于点C,且BD=CD,则∠BAD=∠CAD.
试利用上述知识,解决下面的问题:三条公路两两相交于E,F,G三点,如图2所示,现计划修建一个商品超市,要求这个超市到三条公路的距离相等.问:可供选择的地方有多少处?你能找出来吗?
如图,已知在△ABC中,AB=AC.
(1)作图:在AC上有一点D,延长BD,并在BD的延长线上取点E,使AE=AB,连接AE,作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接CF,求证:∠E=∠ACF.
【操作与发现】如图①,△MNQ中,MQ≠NQ.请你以MN为一边,在MN的同侧构造一个与△MNQ全等的三角形,画出图形,并简要说明构造的方法;
【借鉴与应用】参考你画图构造全等三角形的方法
解决下面问题:
如图②,在四边形ABCD中,∠ACB+∠CAD=180°,∠B=∠D,求证:CD=AB.
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】②①③
10.【答案】2
11.【答案】2
12.【答案】
13.【答案】解:到线段两个端点距离相等的点在线段的垂直平分线上,两点确定一条直线
14.【答案】解:如图所示,∠AOB即为所求.
15.【答案】解:如图所示,即为所求.
16.【答案】解:作AB的垂直平分线,以点C为圆心,以AB长的一半为半径画弧交AB的垂直平分线于点M,则点M即为所求.如图所示.
17.【答案】解:如图,点或点即为所求作的点.(两种情况只要考虑到一种即可)
18.【答案】解:如图所示.
(1)作出△EFG两内角的平分线,其交点为Q1;
(2)分别作出△EFG的外角的平分线,其交点分别为Q2,Q3,Q4,
故满足条件的修建点有四处,即Q1,Q2,Q3,Q4.
19.【答案】(1)解:如图所示;
(2)证明:连接CF,如图,
∵AB=AC,AE=AB,
∴AE=AC,
∵AF是∠EAC的平分线,
∴∠EAF=∠CAF,
在△AEF和△ACF中,
,
∴△AEF≌△ACF(SAS),
∴∠E=∠ACF.
20.【答案】解:【操作与发现】如图①,作∠MNP=∠NMQ,截取NP=MQ,连接PM,则△PMN即为所作.
【借鉴与应用】构建△EAC≌△DCA,如图②,
∴∠ECA=∠DAC,AE=CD,∠E=∠D.
∵∠ACB+∠CAD=180°,∴∠ACB+∠ECA=180°,
∴E点在BC的延长线上.∵∠B=∠D,∴∠E=∠B,
过点A作BE的高,交BE于点F.
在Rt△AFE和Rt△AFB中,
∴Rt△AFE≌Rt△AFB(AAS).
∴AE=AB,
∴CD=AB.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共40分)
给出下列关于三角形的条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角.利用尺规作图,能作出唯一的三角形的条件是()
A. B. C. D.
根据SAS用尺规作三角形,在作图过程中的依据是()
A. 用尺规作一条线段等于已知线段
B. 用尺规作一个角等于已知角
C. 用尺规作一条线段等于已知线段和作一个角等于已知角
D. 不能确定
如图,已知ABC,用尺规作ABC的平分线.如图,步骤如下:
第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在ABC内部交于点P;
第三步:画射线BP,射线BP即为所求.
下列正确的是( )
A. ,均无限制 B. ,的长
C. 有最小限制,无限制 D. ,的长
如图,点C在∠AOB的边OB上,用尺规作出了CN // OA,作图痕迹中,弧FG是 ( )
A. 以点为圆心,为半径的弧 B. 以点为圆心,为半径的弧
C. 以点为圆心,为半径的弧 D. 以点为圆心,为半径的弧
下列尺规作图中,能判断AD是△ABC边上的高的是()
A. B.
C. D.
如图,ABC中,AC< BC,如果用尺规作图的方法在BC上确定点P,使PA+PC=BC,那么符合要求的作图痕迹是( )
A. B.
C. D.
如图,已知AB=AC,AB=5,BC=3,以A,B两点为圆心,大于的长为半径画圆弧,两弧相交于点M,N,连接MN与AC相交于点D,则△BDC的周长为 ( )
A. B.
C. D.
下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线,则对应选项中作法错误的是 ( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下面作法的合理顺序为 .
①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;②作直线BP,在BP上截取BC=a;③连接AB,AC,△ABC为所求作的三角形.
如图,在∠AOB的两边OA,OB上分别截取OM,ON,使OM=ON;再分别以点M,N为圆心,以大于的长为半径作圆弧,两弧交于点E,过点E作EC⊥OA于点C.若EC=2,则点E到直线OB的距离是________.
如图,在RtABC中,B=,以点A为圆心,适当的长为半径画弧,分别交AB、AC于点D、E,再分别以点D、E为圆心,大于DE的长为半径画弧,两弧交于点F,作射线AF交边BC于点G.若BG=1,AC=4,则ACG的面积为 .
如图,在RtABC中,ABC=,根据尺规作图的痕迹判断以下结论:DB=DE;AB=AE;EDC=BAC;DAC=C.其中,错误的是 (填序号).
三、解答题(本大题共8小题,共60分)
阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线.
已知:线段AB.
小芸的作法如下:
(1)分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于C,D两点;
(2)作直线CD.
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是__________________________________________________________________________.
如图,已知∠α和∠β,求作∠α+∠β.
请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知:∠α,直线l及l上两点A,B.
求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
为进一步打造“宜居城市”,某市拟在新竣工的长方形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图所示.请在原图上利用尺规作图作出音乐喷泉M的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
如图,已知四边形ABCD.求作:点P,使PCB=B,且点P到边AD和CD的距离相等.
角平分线上的点到角的两边的距离相等,到角的两边的距离相等的点在角的平分线上,如图1所示.
(1)若∠BAD=∠CAD,且DB⊥AB于点B,DC⊥AC于点C,则BD=CD;
(2)若DB⊥AB于点B,DC⊥AC于点C,且BD=CD,则∠BAD=∠CAD.
试利用上述知识,解决下面的问题:三条公路两两相交于E,F,G三点,如图2所示,现计划修建一个商品超市,要求这个超市到三条公路的距离相等.问:可供选择的地方有多少处?你能找出来吗?
如图,已知在△ABC中,AB=AC.
(1)作图:在AC上有一点D,延长BD,并在BD的延长线上取点E,使AE=AB,连接AE,作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接CF,求证:∠E=∠ACF.
【操作与发现】如图①,△MNQ中,MQ≠NQ.请你以MN为一边,在MN的同侧构造一个与△MNQ全等的三角形,画出图形,并简要说明构造的方法;
【借鉴与应用】参考你画图构造全等三角形的方法
解决下面问题:
如图②,在四边形ABCD中,∠ACB+∠CAD=180°,∠B=∠D,求证:CD=AB.
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】②①③
10.【答案】2
11.【答案】2
12.【答案】
13.【答案】解:到线段两个端点距离相等的点在线段的垂直平分线上,两点确定一条直线
14.【答案】解:如图所示,∠AOB即为所求.
15.【答案】解:如图所示,即为所求.
16.【答案】解:作AB的垂直平分线,以点C为圆心,以AB长的一半为半径画弧交AB的垂直平分线于点M,则点M即为所求.如图所示.
17.【答案】解:如图,点或点即为所求作的点.(两种情况只要考虑到一种即可)
18.【答案】解:如图所示.
(1)作出△EFG两内角的平分线,其交点为Q1;
(2)分别作出△EFG的外角的平分线,其交点分别为Q2,Q3,Q4,
故满足条件的修建点有四处,即Q1,Q2,Q3,Q4.
19.【答案】(1)解:如图所示;
(2)证明:连接CF,如图,
∵AB=AC,AE=AB,
∴AE=AC,
∵AF是∠EAC的平分线,
∴∠EAF=∠CAF,
在△AEF和△ACF中,
,
∴△AEF≌△ACF(SAS),
∴∠E=∠ACF.
20.【答案】解:【操作与发现】如图①,作∠MNP=∠NMQ,截取NP=MQ,连接PM,则△PMN即为所作.
【借鉴与应用】构建△EAC≌△DCA,如图②,
∴∠ECA=∠DAC,AE=CD,∠E=∠D.
∵∠ACB+∠CAD=180°,∴∠ACB+∠ECA=180°,
∴E点在BC的延长线上.∵∠B=∠D,∴∠E=∠B,
过点A作BE的高,交BE于点F.
在Rt△AFE和Rt△AFB中,
∴Rt△AFE≌Rt△AFB(AAS).
∴AE=AB,
∴CD=AB.
第2页,共3页
同课章节目录
