2021-2022学年人教版数学九年级上册24.2.1点和圆的位置关系-课堂练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.2.1点和圆的位置关系-课堂练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 359.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 00:00:00 | ||
图片预览


文档简介
2021-2022学年初中(人教版)数学九年级上册
24.2.1点和圆的位置关系-课堂练习
时间:40分钟
一、单选题
1.在同一平面内,过已知A,B,C三个点可以作的圆的个数为( )
A.0 B.1 C.2 D.0或1
2.如图,为锐角三角形的外心,四边形为正方形,其中点在的外部,判断下列叙述正确的是( )
A.是的外心,是的外心 B.是的外心,不是的外心
C.不是的外心,是的外心 D.不是的外心,不是的外心
3.已知中,,,,点P为边AB的中点,以点C为圆心,长度r为半径画圆,使得点A,P在⊙C内,点B在⊙C外,则半径r的取值范围是( )
A. B. C. D.
4.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
5.下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③三角形的外心是各边垂直平分线的交点;④三角形的外心到三角形三边的距离相等;⑤等腰三角形的外心一定在这个三角形内,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.在平面直角坐标系中,⊙O的半径为2,点A(1,)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
二、填空题
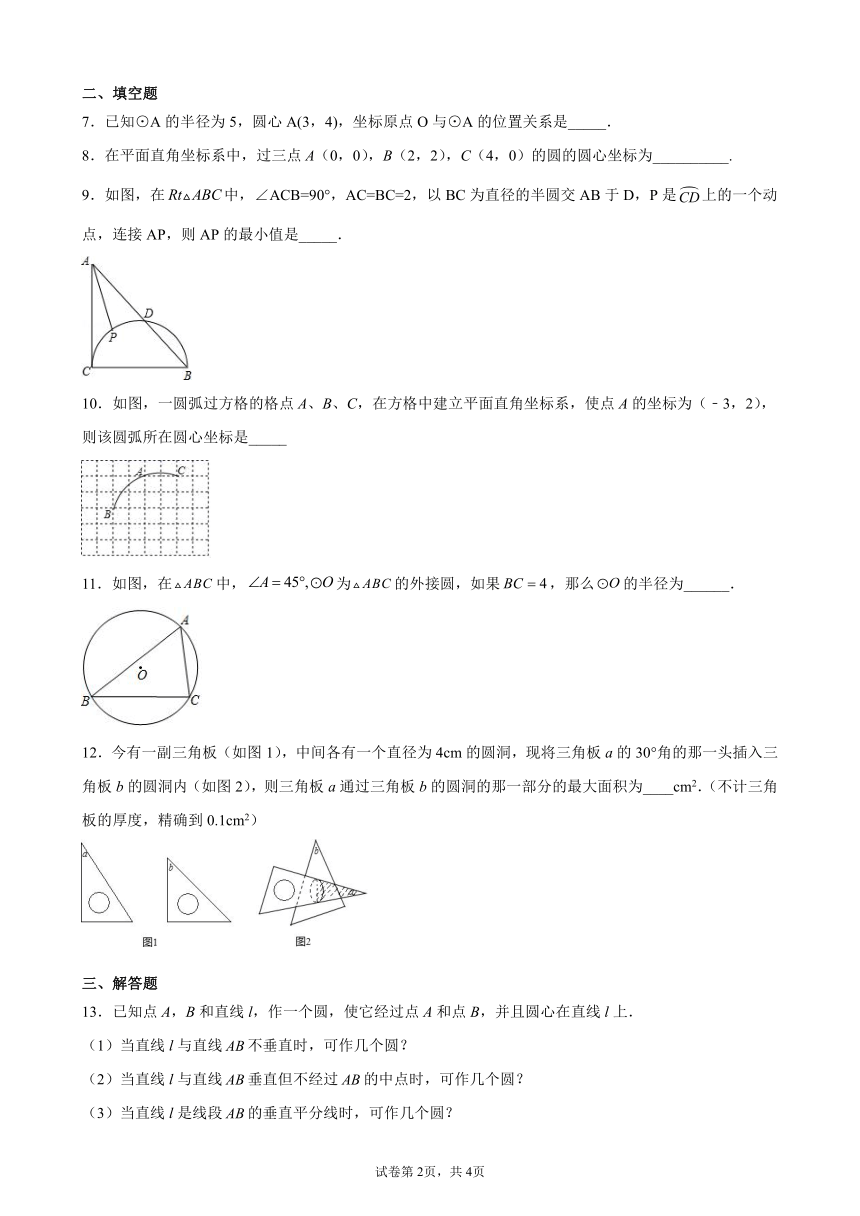
7.已知⊙A的半径为5,圆心A(3,4),坐标原点O与⊙A的位置关系是_____.
8.在平面直角坐标系中,过三点A(0,0),B(2,2),C(4,0)的圆的圆心坐标为__________.
9.如图,在中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是_____.
10.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(﹣3,2),则该圆弧所在圆心坐标是_____
11.如图,在中,为的外接圆,如果,那么的半径为______.
12.今有一副三角板(如图1),中间各有一个直径为4cm的圆洞,现将三角板a的30°角的那一头插入三角板b的圆洞内(如图2),则三角板a通过三角板b的圆洞的那一部分的最大面积为____cm2.(不计三角板的厚度,精确到0.1cm2)
三、解答题
13.已知点A,B和直线l,作一个圆,使它经过点A和点B,并且圆心在直线l上.
(1)当直线l与直线不垂直时,可作几个圆?
(2)当直线l与直线垂直但不经过的中点时,可作几个圆?
(3)当直线l是线段的垂直平分线时,可作几个圆?
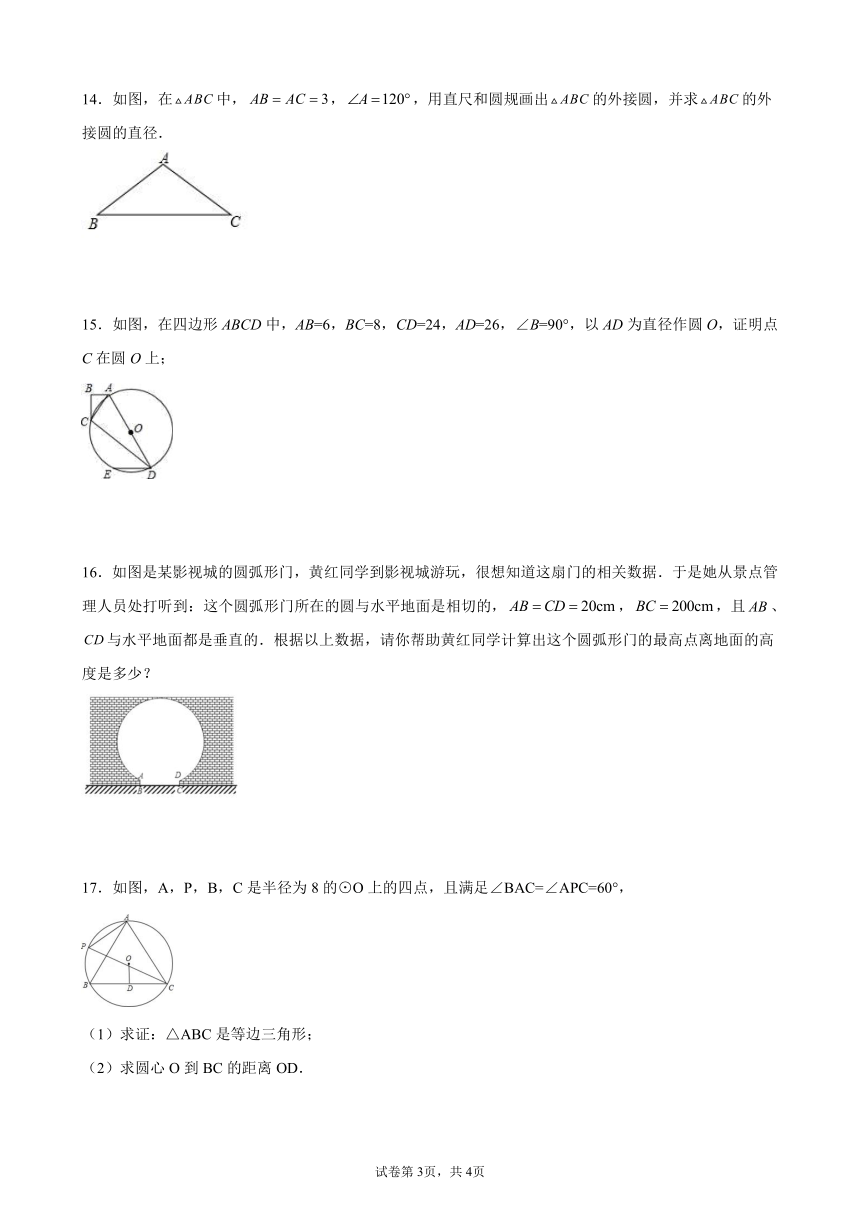
14.如图,在中,,,用直尺和圆规画出的外接圆,并求的外接圆的直径.
15.如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,证明点C在圆O上;
16.如图是某影视城的圆弧形门,黄红同学到影视城游玩,很想知道这扇门的相关数据.于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,,,且、与水平地面都是垂直的.根据以上数据,请你帮助黄红同学计算出这个圆弧形门的最高点离地面的高度是多少?
17.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
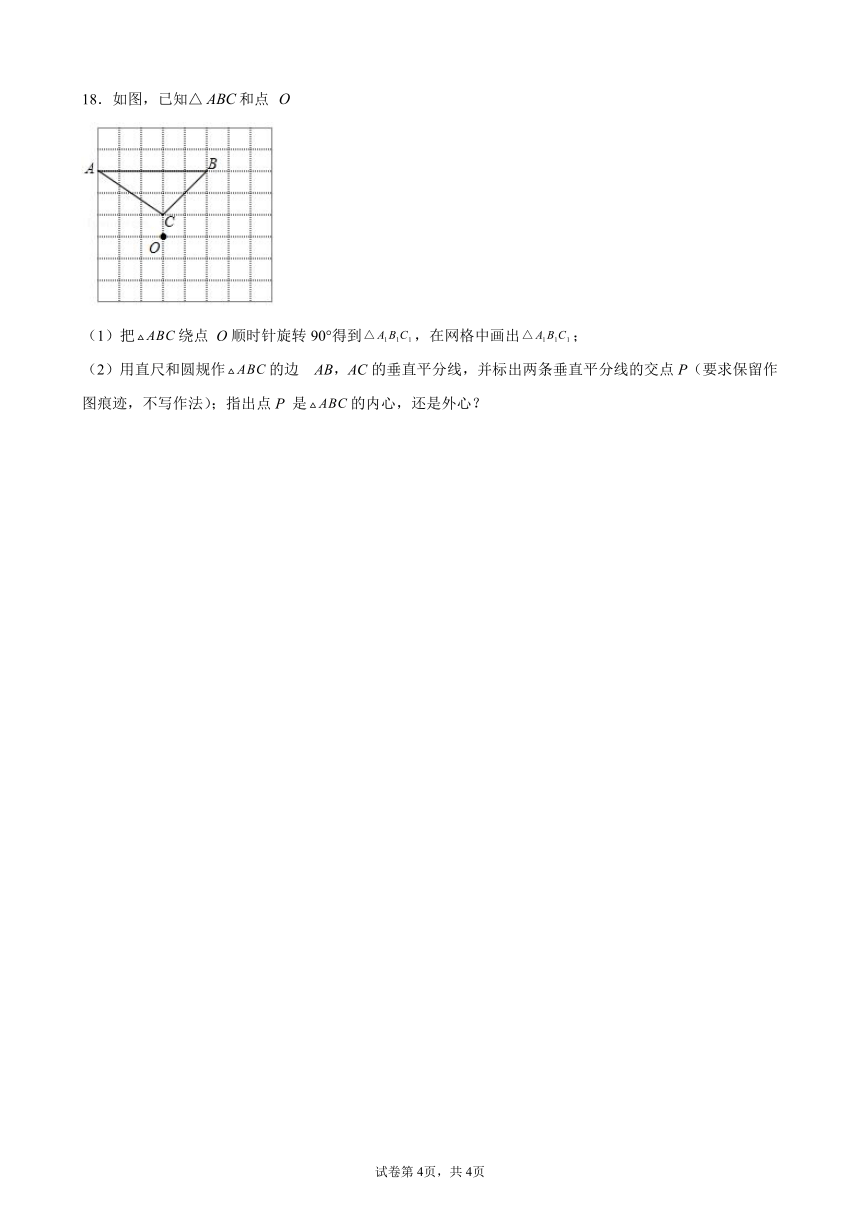
18.如图,已知△和点
(1)把绕点 O顺时针旋转90°得到,在网格中画出;
(2)用直尺和圆规作的边 AB,AC的垂直平分线,并标出两条垂直平分线的交点P(要求保留作图痕迹,不写作法);指出点P 是的内心,还是外心?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:当A、B、C三个点共线,过A、B、C三个点不能作圆;
当A、B、C不在同一条直线上,过A、B、C三个点的圆有且只有一个,即三角形的外接圆;
故选D.
2.B
【解析】解析:如图,连接,,,
∵是的外心,
∴,
∵四边形是正方形,
∴,
∴是的外心,
∵,
∴不是的外心,
故选:B.
3.D
【解析】∵点A在⊙C内,
∴r>3,
∵点B在⊙C外,
∴r<4,
∴,
故选:D.
4.A
【解析】解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
5.B
【解析】解:②③正确;不在同一直线上的三点确定一个圆,所以①错误;三角形的外心到三角形三个顶点的距离相等,所以④错误;当等腰三角形是钝角三角形时,它的外心在这个三角形外;当等腰三角形是直角三角形时,它的外心在这个三角形的斜边上,所以⑤错误,
∴正确的有②③,
故选:B.
6.A
【解析】解:∵点A的坐标为(1,),
∴由勾股定理可得:OA=,
又∵⊙O的半径为2,
∴点A在⊙O上.
故选:A.
7.在⊙A上.
【解析】∵点A的坐标为(4,3),∴OA=,
∵半径为5,而5=5,∴点O在⊙A上.
故答案为在⊙A上.
8.(2,0)
【解析】解:过点B作BD⊥AC,
∵A(0,0),B(2,2),
∴BD=AD=2,
∴∠ABD=∠BAD=45°,
又∵C(4,0),
∴CD=AD=2=BD,
∴∠DCB=∠DBC=45°,
∴∠ABC=90°,
∴点A、B、C三点在以点D为圆心,AD长为半径的圆上,
所以圆心的坐标为(2,0),
故答案为(2,0).
9..
【解析】找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE=,P2E=1,
∴AP2=.
10.(﹣2,﹣1)
【解析】如图:分别作AC与AB的垂直平分线,相交于点O,
则点O即是该圆弧所在圆的圆心.
∵点A的坐标为(﹣3,2),∴点O的坐标为(﹣2,﹣1).
11.
【解析】解:连接、,作,
,
,
又∵OB=OC,,,
,
∴在中,,
故答案为:.
12.14.9
【解析】假设三角板a通过三角板b的圆洞的那一部分为△ABC,BC=4cm,∠BAC=30°,
作△ABC的外接圆⊙P,连接PA,PB,PC,作PD⊥BC于D,则PB=PC=PA.
∵∠BAC=30°,
∴∠BPC=2∠BAC=60°,
∴△PBC是等边三角形,
∴BD=CD=2,PD=,BP=BC=PA=4,
连接AD,则AD≤AP+PD=4+,
∴当A,P,D在同一直线上时,AD有最大值,
此时,AD⊥BC,
∴S△ABC=×BC×AD=×4×(4+)=8+≈14.9(cm2).
故答案为:14.9.
13.(1)1个;(2)0个;(3)无数个.
【解析】解:(1)如图1,过A、B的圆的圆心在线段AB垂直平分线m上,而直线m与直线l只有1个交点,
∴当直线l与直线AB不垂直时,只能作1个圆;
(2)如图2,过A、B的圆的圆心在线段AB垂直平分线m上,而直线m与直线l没有个交点,
∴当直线l与直线AB垂直但不经过AB的中点时,不能作圆;
(3)如图3,过A、B的圆的圆心在线段AB垂直平分线m上,而直线m与直线l重合,即直线l上所有点均可作为经过A,B的圆的圆心,
∴当直线l是线段AB的垂直平分线时,能作无数个圆.
14.见解析,外接圆的直径为6
【解析】解:分别作线段、的垂直平分线交于点,以点为圆心,长为半径画圆,则就是的外接圆,如下图所示:
如图,连接,知垂直平分,交于点,
∵,
∴,,
连接,
∵,
∴为等边三角形,
∴,
∴的外接圆的直径为6.
15.证明见解析
【解析】如图,连接CO
∵AB=6,BC=8,∠B=90°,
∴
∵CD=24,AD=26
∴
∴△ACD是直角三角形,
∴∠ACD=90°
∵AD为⊙O的直径
∴AO=OD
∴OC为Rt△ACD斜边上的中线
∴
∴点C在圆O上.
16.
【解析】设其切点为F,连,交于点E
∵是的切线
∴
∵四边形是矩形
∴
∴,.
设半径为r,
在中,
∴
∵即
∴
答:圆弧形门的最高点离地面的高度为.
17.(1)证明见解析(2)4
【解析】解:(1)证明:∵∠APC和∠ABC是同弧所对的圆周角,∴∠APC=∠ABC.
又∵在△ABC中,∠BAC=∠APC=60°,∴∠ABC=60°.
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°.
∴△ABC是等边三角形.
(2)连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心.
∴BO平分∠ABC.∴∠OBD=30°.∴OD=8×=4.
18.(1)见解析;(2)图见解析,外心
【解析】(1)△ 如图所示;
(2)如图所示;点P 是的外心.
答案第1页,共2页
答案第1页,共2页
24.2.1点和圆的位置关系-课堂练习
时间:40分钟
一、单选题
1.在同一平面内,过已知A,B,C三个点可以作的圆的个数为( )
A.0 B.1 C.2 D.0或1
2.如图,为锐角三角形的外心,四边形为正方形,其中点在的外部,判断下列叙述正确的是( )
A.是的外心,是的外心 B.是的外心,不是的外心
C.不是的外心,是的外心 D.不是的外心,不是的外心
3.已知中,,,,点P为边AB的中点,以点C为圆心,长度r为半径画圆,使得点A,P在⊙C内,点B在⊙C外,则半径r的取值范围是( )
A. B. C. D.
4.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
5.下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③三角形的外心是各边垂直平分线的交点;④三角形的外心到三角形三边的距离相等;⑤等腰三角形的外心一定在这个三角形内,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.在平面直角坐标系中,⊙O的半径为2,点A(1,)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
二、填空题
7.已知⊙A的半径为5,圆心A(3,4),坐标原点O与⊙A的位置关系是_____.
8.在平面直角坐标系中,过三点A(0,0),B(2,2),C(4,0)的圆的圆心坐标为__________.
9.如图,在中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是_____.
10.如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(﹣3,2),则该圆弧所在圆心坐标是_____
11.如图,在中,为的外接圆,如果,那么的半径为______.
12.今有一副三角板(如图1),中间各有一个直径为4cm的圆洞,现将三角板a的30°角的那一头插入三角板b的圆洞内(如图2),则三角板a通过三角板b的圆洞的那一部分的最大面积为____cm2.(不计三角板的厚度,精确到0.1cm2)
三、解答题
13.已知点A,B和直线l,作一个圆,使它经过点A和点B,并且圆心在直线l上.
(1)当直线l与直线不垂直时,可作几个圆?
(2)当直线l与直线垂直但不经过的中点时,可作几个圆?
(3)当直线l是线段的垂直平分线时,可作几个圆?
14.如图,在中,,,用直尺和圆规画出的外接圆,并求的外接圆的直径.
15.如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,证明点C在圆O上;
16.如图是某影视城的圆弧形门,黄红同学到影视城游玩,很想知道这扇门的相关数据.于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,,,且、与水平地面都是垂直的.根据以上数据,请你帮助黄红同学计算出这个圆弧形门的最高点离地面的高度是多少?
17.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
18.如图,已知△和点
(1)把绕点 O顺时针旋转90°得到,在网格中画出;
(2)用直尺和圆规作的边 AB,AC的垂直平分线,并标出两条垂直平分线的交点P(要求保留作图痕迹,不写作法);指出点P 是的内心,还是外心?
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.D
【解析】解:当A、B、C三个点共线,过A、B、C三个点不能作圆;
当A、B、C不在同一条直线上,过A、B、C三个点的圆有且只有一个,即三角形的外接圆;
故选D.
2.B
【解析】解析:如图,连接,,,
∵是的外心,
∴,
∵四边形是正方形,
∴,
∴是的外心,
∵,
∴不是的外心,
故选:B.
3.D
【解析】∵点A在⊙C内,
∴r>3,
∵点B在⊙C外,
∴r<4,
∴,
故选:D.
4.A
【解析】解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
5.B
【解析】解:②③正确;不在同一直线上的三点确定一个圆,所以①错误;三角形的外心到三角形三个顶点的距离相等,所以④错误;当等腰三角形是钝角三角形时,它的外心在这个三角形外;当等腰三角形是直角三角形时,它的外心在这个三角形的斜边上,所以⑤错误,
∴正确的有②③,
故选:B.
6.A
【解析】解:∵点A的坐标为(1,),
∴由勾股定理可得:OA=,
又∵⊙O的半径为2,
∴点A在⊙O上.
故选:A.
7.在⊙A上.
【解析】∵点A的坐标为(4,3),∴OA=,
∵半径为5,而5=5,∴点O在⊙A上.
故答案为在⊙A上.
8.(2,0)
【解析】解:过点B作BD⊥AC,
∵A(0,0),B(2,2),
∴BD=AD=2,
∴∠ABD=∠BAD=45°,
又∵C(4,0),
∴CD=AD=2=BD,
∴∠DCB=∠DBC=45°,
∴∠ABC=90°,
∴点A、B、C三点在以点D为圆心,AD长为半径的圆上,
所以圆心的坐标为(2,0),
故答案为(2,0).
9..
【解析】找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE=,P2E=1,
∴AP2=.
10.(﹣2,﹣1)
【解析】如图:分别作AC与AB的垂直平分线,相交于点O,
则点O即是该圆弧所在圆的圆心.
∵点A的坐标为(﹣3,2),∴点O的坐标为(﹣2,﹣1).
11.
【解析】解:连接、,作,
,
,
又∵OB=OC,,,
,
∴在中,,
故答案为:.
12.14.9
【解析】假设三角板a通过三角板b的圆洞的那一部分为△ABC,BC=4cm,∠BAC=30°,
作△ABC的外接圆⊙P,连接PA,PB,PC,作PD⊥BC于D,则PB=PC=PA.
∵∠BAC=30°,
∴∠BPC=2∠BAC=60°,
∴△PBC是等边三角形,
∴BD=CD=2,PD=,BP=BC=PA=4,
连接AD,则AD≤AP+PD=4+,
∴当A,P,D在同一直线上时,AD有最大值,
此时,AD⊥BC,
∴S△ABC=×BC×AD=×4×(4+)=8+≈14.9(cm2).
故答案为:14.9.
13.(1)1个;(2)0个;(3)无数个.
【解析】解:(1)如图1,过A、B的圆的圆心在线段AB垂直平分线m上,而直线m与直线l只有1个交点,
∴当直线l与直线AB不垂直时,只能作1个圆;
(2)如图2,过A、B的圆的圆心在线段AB垂直平分线m上,而直线m与直线l没有个交点,
∴当直线l与直线AB垂直但不经过AB的中点时,不能作圆;
(3)如图3,过A、B的圆的圆心在线段AB垂直平分线m上,而直线m与直线l重合,即直线l上所有点均可作为经过A,B的圆的圆心,
∴当直线l是线段AB的垂直平分线时,能作无数个圆.
14.见解析,外接圆的直径为6
【解析】解:分别作线段、的垂直平分线交于点,以点为圆心,长为半径画圆,则就是的外接圆,如下图所示:
如图,连接,知垂直平分,交于点,
∵,
∴,,
连接,
∵,
∴为等边三角形,
∴,
∴的外接圆的直径为6.
15.证明见解析
【解析】如图,连接CO
∵AB=6,BC=8,∠B=90°,
∴
∵CD=24,AD=26
∴
∴△ACD是直角三角形,
∴∠ACD=90°
∵AD为⊙O的直径
∴AO=OD
∴OC为Rt△ACD斜边上的中线
∴
∴点C在圆O上.
16.
【解析】设其切点为F,连,交于点E
∵是的切线
∴
∵四边形是矩形
∴
∴,.
设半径为r,
在中,
∴
∵即
∴
答:圆弧形门的最高点离地面的高度为.
17.(1)证明见解析(2)4
【解析】解:(1)证明:∵∠APC和∠ABC是同弧所对的圆周角,∴∠APC=∠ABC.
又∵在△ABC中,∠BAC=∠APC=60°,∴∠ABC=60°.
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°.
∴△ABC是等边三角形.
(2)连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心.
∴BO平分∠ABC.∴∠OBD=30°.∴OD=8×=4.
18.(1)见解析;(2)图见解析,外心
【解析】(1)△ 如图所示;
(2)如图所示;点P 是的外心.
答案第1页,共2页
答案第1页,共2页
同课章节目录
