2021-2022学年人教版数学九年级上册24.4弧长和扇形面积-课堂练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.4弧长和扇形面积-课堂练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 510.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 10:27:32 | ||
图片预览



文档简介
2021-2022学年初中(人教版)数学九年级上册
24.4弧长和扇形面积-课堂练习
时间:40分钟
一、单选题
1.在圆心角为的扇形中,半径,则扇形的面积是( )
A. B. C. D.
2.一个滑轮起重装置如图所示,滑轮的半径是15cm,当重物上升15cn时,滑轮的一条半径OA绕轴心O按顺时针方向旋转的角度约为( )(π取3.14,结果精确到1 )
A.115 B.60 C.57 D.29
3.如图,正方形的边长,分别以点,为圆心,长为半径画弧,两弧交于点,则的长是( )
A. B. C. D.
4.如图,正方形的边长为4,以点为圆心,为半径画圆弧得到扇形(阴影部分,点在对角线上).若扇形正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A. B.1 C. D.
5.如图,在中,,,以的中点为圆心,作圆心角为的扇形,点恰在上,设,当由小到大变化时,图中阴影部分的面积为( )
A. B. C. D.随的变化而变化
6.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
二、填空题
7.如图是一个圆锥形雪糕冰激凌外壳(不计厚度),已知其母线长为,底面圆半径为.则这个冰激凌外壳的侧面积等于_______.(结果保留)
8.已知60°的圆心角所对的弧长为3cm,它所在的圆的周长是_________cm.
9.如图,扇形中,.若将此扇形绕点B顺时针旋转,得一新扇形,其中A点在上,则点O的运动路径长为_______.(结果保留)
10.用一块半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则此圆锥的高为_____.
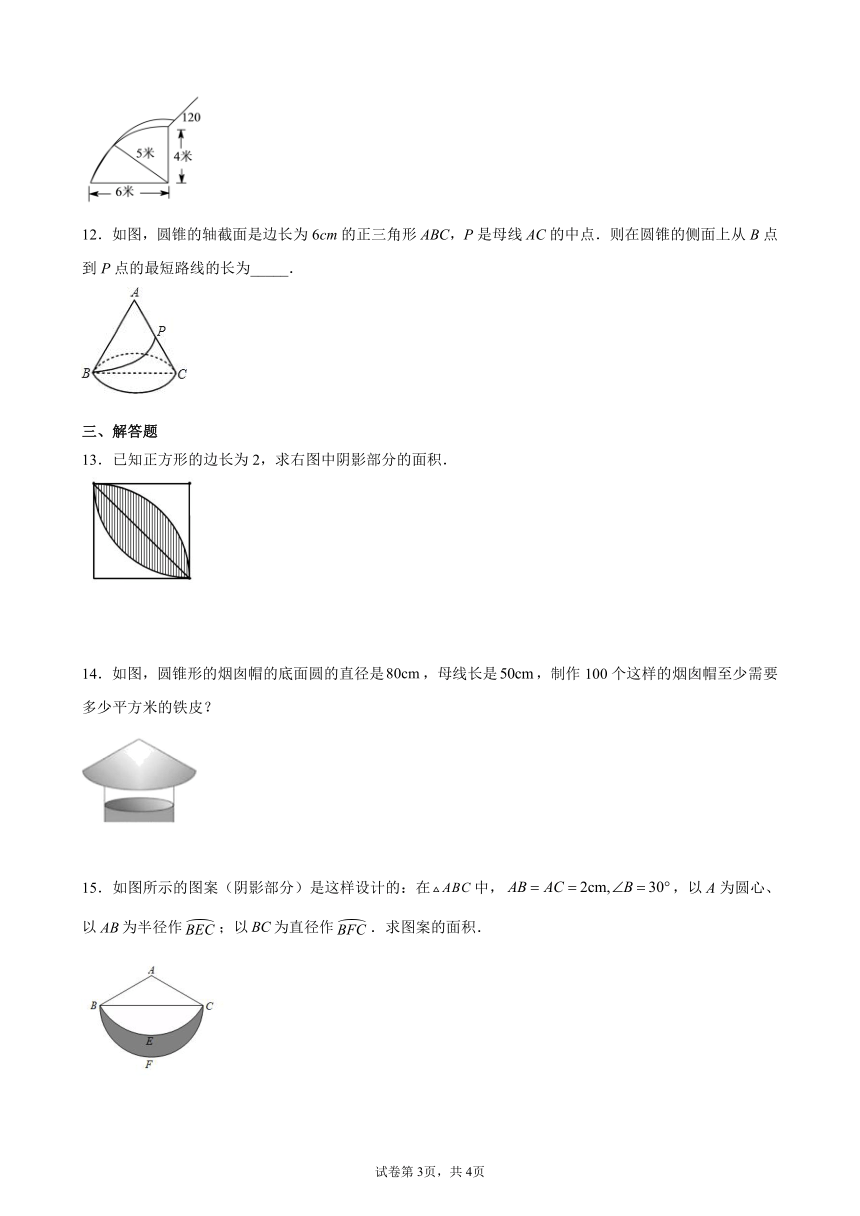
11.如图,一根长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊(羊只能在草地上活动),那么小羊在草地上的最大活动区域面积是__________平方米.
12.如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点.则在圆锥的侧面上从B点到P点的最短路线的长为_____.
三、解答题
13.已知正方形的边长为2,求右图中阴影部分的面积.
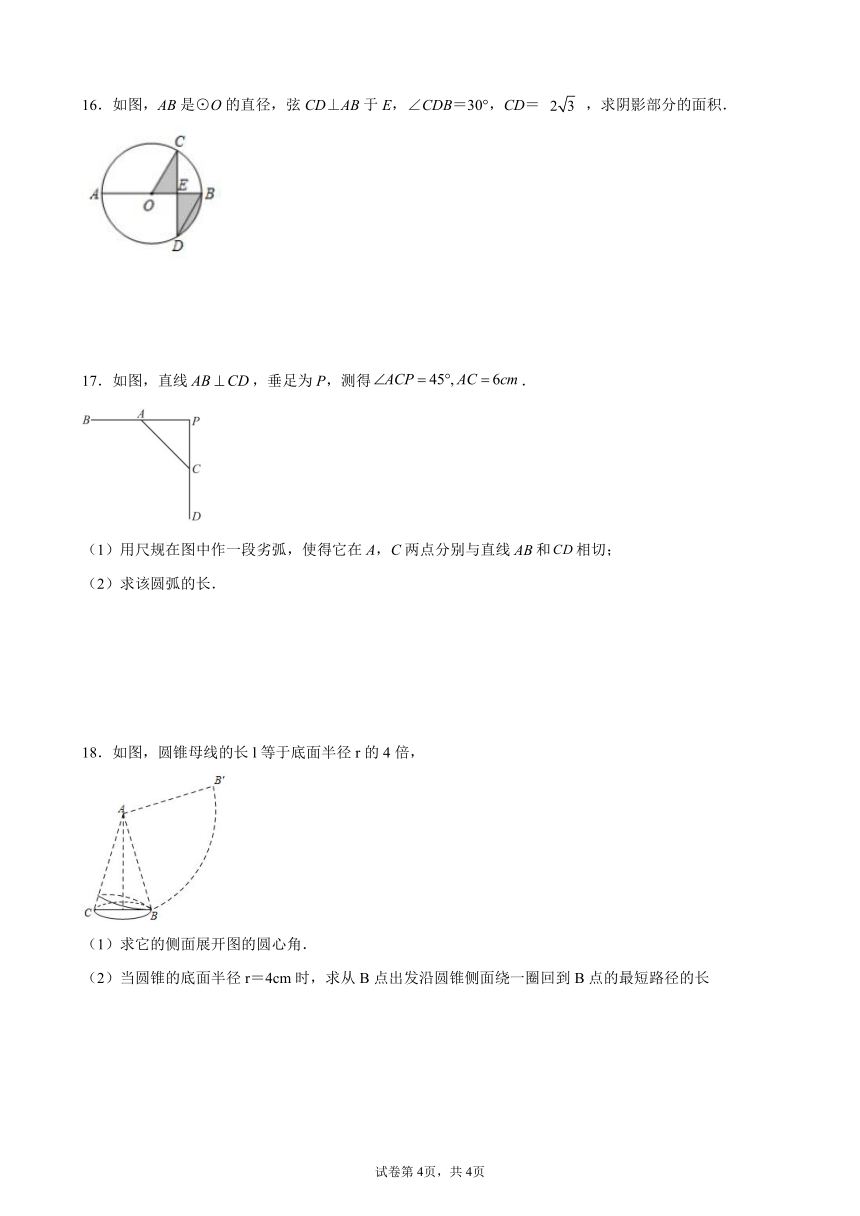
14.如图,圆锥形的烟囱帽的底面圆的直径是,母线长是,制作100个这样的烟囱帽至少需要多少平方米的铁皮?
15.如图所示的图案(阴影部分)是这样设计的:在中,,以A为圆心、以为半径作;以为直径作.求图案的面积.
16.如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.
17.如图,直线,垂足为P,测得.
(1)用尺规在图中作一段劣弧,使得它在A,C两点分别与直线和相切;
(2)求该圆弧的长.
18.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:由题意得扇形的面积是.
故选C.
2.C
【解析】设OA旋转的角度为n,由于重物上升15 cm,
则点A顺时针旋转的弧长为15 cm,
由弧长公式l=,
可求n=≈57度.
故选C.
3.A
【解析】解:连接,,
∵,
∴是等边三角形.
∴,
∴,
∴的长为.
故选A.
4.D
【解析】∵正方形的边长为4
∴
∵是正方形的对角线
∴
∴
∴圆锥底面周长为,解得
∴该圆锥的底面圆的半径是,
故选:D.
5.C
【解析】如图,连接,作于点,于点,
∵,,∴,
,,∴,
∴四边形是正方形,
∴,∴,
∵,∴,
∴,
在和中,
,
∴,
∴四边形的面积正方形的面积,
∵正方形的面积,
∴四边形的面积,
∵扇形的面积,
∴阴影部分的面积扇形的面积四边形的面积,恒为定值.
故选:C.
6.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
7.
【解析】这个冰激凌外壳的侧面积为,
故答案为.
8.18
【解析】.
故答案为:18.
9.4π.
【解析】解:根据题意,知OA=OB.
又∠AOB=36°,
∴∠OBA=72°.
∴点O旋转至O′点所经过的轨迹长度==4πcm.
故答案是:4π.
10.
【解析】
设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=1,
所以此圆锥的高=,
故答案为:.
11..
【解析】解:如图.小羊的活动范围是:(平方米)
故答案为.
12.3.
【解析】解:圆锥底面是以BC为直径的圆,圆的周长是BCπ=6π,
以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则,
解得:n=180,
即展开后∠BAC=×180°=90°,
AP=AC=3,AB=6,
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
由勾股定理得:BP=,
故答案为:.
13.2.28
【解析】解:根据题意,则
.
14.100个这样的烟囱帽至少需要20πm2的铁皮.
【解析】解:圆锥形的烟囱帽的侧面积= 80π 50=2000π(cm2),
100×2000π=200000π(cm2)=20π(m2)
答:100个这样的烟囱帽至少需要20πm2的铁皮.
15..
【解析】解:如图,过点A作于点,
,,
,,
,
∵在中,,,
,
∴,
∴,
图案的面积
,
∴该图案的面积为.
16.
【解析】解:连接OD.
∵CD⊥AB,
∴CE=DE=CD=(垂径定理),弧BC=弧BD
故S△OCE=S△ODE,∠COB=∠DOB,
∴S阴=S扇形OBD ,
又∵∠CDB=30°,
∴∠COB=∠DOB=60°(圆周角定理),
∴∠OCB=30°
∴OC=,
解得:,
故S扇形OBD= =,
即阴影部分的面积为.
17.(1)答案见解析;(2).
【解析】解:(1)分别从点A,C处作垂线,两垂线相交于点O,以点O为圆心,OA为半径作圆,弧AC就是所求的劣弧;
(2)由题意及作图过程可得:∠AOC=90°,
∵∠ACP=45°,AC=6cm,
∴OA==cm,
∴弧AC==cm.
18.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【解析】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
答案第1页,共2页
答案第1页,共2页
24.4弧长和扇形面积-课堂练习
时间:40分钟
一、单选题
1.在圆心角为的扇形中,半径,则扇形的面积是( )
A. B. C. D.
2.一个滑轮起重装置如图所示,滑轮的半径是15cm,当重物上升15cn时,滑轮的一条半径OA绕轴心O按顺时针方向旋转的角度约为( )(π取3.14,结果精确到1 )
A.115 B.60 C.57 D.29
3.如图,正方形的边长,分别以点,为圆心,长为半径画弧,两弧交于点,则的长是( )
A. B. C. D.
4.如图,正方形的边长为4,以点为圆心,为半径画圆弧得到扇形(阴影部分,点在对角线上).若扇形正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A. B.1 C. D.
5.如图,在中,,,以的中点为圆心,作圆心角为的扇形,点恰在上,设,当由小到大变化时,图中阴影部分的面积为( )
A. B. C. D.随的变化而变化
6.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
二、填空题
7.如图是一个圆锥形雪糕冰激凌外壳(不计厚度),已知其母线长为,底面圆半径为.则这个冰激凌外壳的侧面积等于_______.(结果保留)
8.已知60°的圆心角所对的弧长为3cm,它所在的圆的周长是_________cm.
9.如图,扇形中,.若将此扇形绕点B顺时针旋转,得一新扇形,其中A点在上,则点O的运动路径长为_______.(结果保留)
10.用一块半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则此圆锥的高为_____.
11.如图,一根长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊(羊只能在草地上活动),那么小羊在草地上的最大活动区域面积是__________平方米.
12.如图,圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点.则在圆锥的侧面上从B点到P点的最短路线的长为_____.
三、解答题
13.已知正方形的边长为2,求右图中阴影部分的面积.
14.如图,圆锥形的烟囱帽的底面圆的直径是,母线长是,制作100个这样的烟囱帽至少需要多少平方米的铁皮?
15.如图所示的图案(阴影部分)是这样设计的:在中,,以A为圆心、以为半径作;以为直径作.求图案的面积.
16.如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.
17.如图,直线,垂足为P,测得.
(1)用尺规在图中作一段劣弧,使得它在A,C两点分别与直线和相切;
(2)求该圆弧的长.
18.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.C
【解析】解:由题意得扇形的面积是.
故选C.
2.C
【解析】设OA旋转的角度为n,由于重物上升15 cm,
则点A顺时针旋转的弧长为15 cm,
由弧长公式l=,
可求n=≈57度.
故选C.
3.A
【解析】解:连接,,
∵,
∴是等边三角形.
∴,
∴,
∴的长为.
故选A.
4.D
【解析】∵正方形的边长为4
∴
∵是正方形的对角线
∴
∴
∴圆锥底面周长为,解得
∴该圆锥的底面圆的半径是,
故选:D.
5.C
【解析】如图,连接,作于点,于点,
∵,,∴,
,,∴,
∴四边形是正方形,
∴,∴,
∵,∴,
∴,
在和中,
,
∴,
∴四边形的面积正方形的面积,
∵正方形的面积,
∴四边形的面积,
∵扇形的面积,
∴阴影部分的面积扇形的面积四边形的面积,恒为定值.
故选:C.
6.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
7.
【解析】这个冰激凌外壳的侧面积为,
故答案为.
8.18
【解析】.
故答案为:18.
9.4π.
【解析】解:根据题意,知OA=OB.
又∠AOB=36°,
∴∠OBA=72°.
∴点O旋转至O′点所经过的轨迹长度==4πcm.
故答案是:4π.
10.
【解析】
设圆锥的底面圆的半径为r,
根据题意得2πr=,解得r=1,
所以此圆锥的高=,
故答案为:.
11..
【解析】解:如图.小羊的活动范围是:(平方米)
故答案为.
12.3.
【解析】解:圆锥底面是以BC为直径的圆,圆的周长是BCπ=6π,
以AB为一边,将圆锥展开,就得到一个以A为圆心,以AB为半径的扇形,弧长是l=6π,
设展开后的圆心角是n°,则,
解得:n=180,
即展开后∠BAC=×180°=90°,
AP=AC=3,AB=6,
则在圆锥的侧面上从B点到P点的最短路线的长就是展开后线段BP的长,
由勾股定理得:BP=,
故答案为:.
13.2.28
【解析】解:根据题意,则
.
14.100个这样的烟囱帽至少需要20πm2的铁皮.
【解析】解:圆锥形的烟囱帽的侧面积= 80π 50=2000π(cm2),
100×2000π=200000π(cm2)=20π(m2)
答:100个这样的烟囱帽至少需要20πm2的铁皮.
15..
【解析】解:如图,过点A作于点,
,,
,,
,
∵在中,,,
,
∴,
∴,
图案的面积
,
∴该图案的面积为.
16.
【解析】解:连接OD.
∵CD⊥AB,
∴CE=DE=CD=(垂径定理),弧BC=弧BD
故S△OCE=S△ODE,∠COB=∠DOB,
∴S阴=S扇形OBD ,
又∵∠CDB=30°,
∴∠COB=∠DOB=60°(圆周角定理),
∴∠OCB=30°
∴OC=,
解得:,
故S扇形OBD= =,
即阴影部分的面积为.
17.(1)答案见解析;(2).
【解析】解:(1)分别从点A,C处作垂线,两垂线相交于点O,以点O为圆心,OA为半径作圆,弧AC就是所求的劣弧;
(2)由题意及作图过程可得:∠AOC=90°,
∵∠ACP=45°,AC=6cm,
∴OA==cm,
∴弧AC==cm.
18.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【解析】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
答案第1页,共2页
答案第1页,共2页
同课章节目录
