2021-2022学年北师大版九年级数学下册2.4二次函数的应用习题精选(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2.4二次函数的应用习题精选(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 326.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 08:34:02 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册第2章《二次函数的应用》习题精选(附答案)
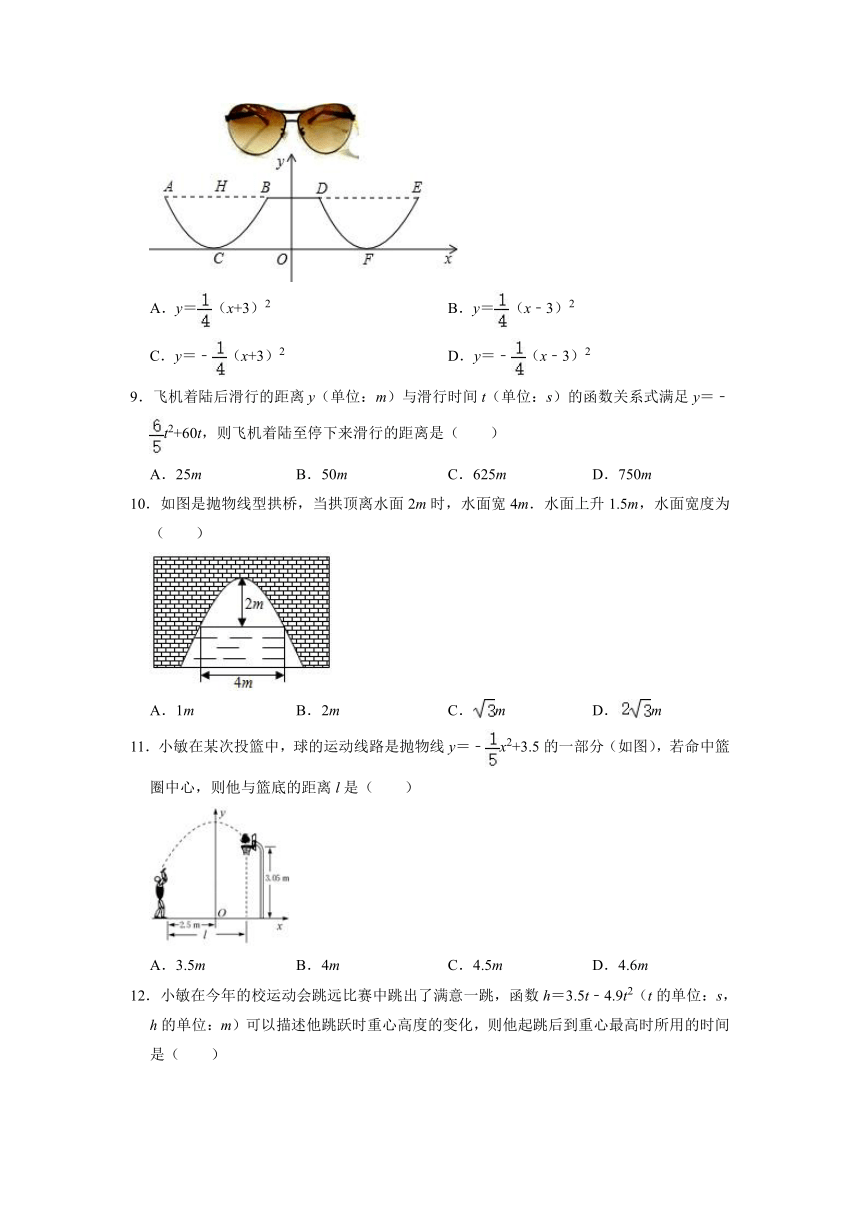
1.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;
④小球的高度h=30m时,t=1.5s.
其中正确的是( )
A.①④ B.①② C.②③④ D.②③
2.跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )
A.10m B.15m C.20m D.22.5m
3.用长8m的铝合金条制成如图形状的矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是( )
A.m2 B.m2 C.m2 D.4m2
4.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④ B.①② C.②③④ D.②④
5.如图,某幢建筑物从2.25米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )
A.2.5米 B.3米 C.3.5米 D.4米
6.黄山市某塑料玩具生产公司,为了减少空气污染,国家要求限制塑料玩具生产,这样有时企业会被迫停产,经过调研预测,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=﹣n2+14n﹣24,则没有盈利的月份为( )
A.2月和12月 B.2月至12月
C.1月 D.1月、2月和12月
7.地面上一个小球被推开后笔直滑行,滑行的距离s与时间t的函数关系如图中的部分抛物线所示(其中P是该抛物线的顶点),则下列说法正确的是( )
A.小球滑行6秒停止 B.小球滑行12秒停止
C.小球滑行6秒回到起点 D.小球滑行12秒回到起点
8.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )
A.y=(x+3)2 B.y=(x﹣3)2
C.y=﹣(x+3)2 D.y=﹣(x﹣3)2
9.飞机着陆后滑行的距离y(单位:m)与滑行时间t(单位:s)的函数关系式满足y=﹣t2+60t,则飞机着陆至停下来滑行的距离是( )
A.25m B.50m C.625m D.750m
10.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面上升1.5m,水面宽度为( )
A.1m B.2m C.m D.m
11.小敏在某次投篮中,球的运动线路是抛物线y=﹣x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离l是( )
A.3.5m B.4m C.4.5m D.4.6m
12.小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h=3.5t﹣4.9t2(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
A.0.71s B.0.70s C.0.63s D.0.36s
13.如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为h=20t﹣5t2,则小球从飞出到落地的所用时间为( )
A.3s B.4s C.5s D.6s
14.在广安市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=﹣x2+x+,由此可知该生此次实心球训练的成绩为 米.
15.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8m,他在不弯腰的情况下,在棚内的横向活动范围是 m.
16.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式y=﹣0.2x2+1.5x﹣2,则最佳加工时间为 min.
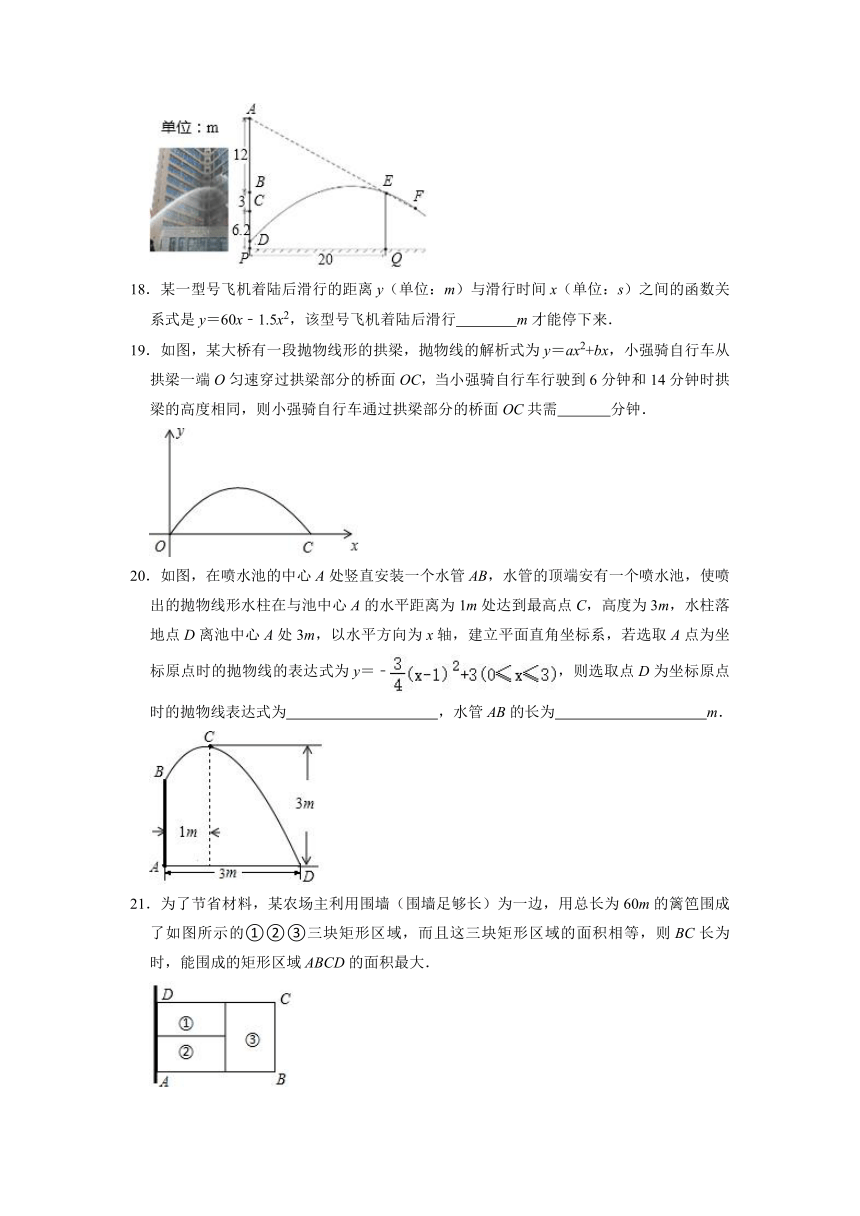
17.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了 m,恰好把水喷到F处进行灭火.
18.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2,该型号飞机着陆后滑行 m才能停下来.
19.如图,某大桥有一段抛物线形的拱梁,抛物线的解析式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶到6分钟和14分钟时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需 分钟.
20.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端安有一个喷水池,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m,水柱落地点D离池中心A处3m,以水平方向为x轴,建立平面直角坐标系,若选取A点为坐标原点时的抛物线的表达式为y=﹣,则选取点D为坐标原点时的抛物线表达式为 ,水管AB的长为 m.
21.为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为60m的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则BC长为 时,能围成的矩形区域ABCD的面积最大.
22.为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
23.“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,如图所示.
(1)求y与x之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
24.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
25.某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
26.俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为y本,销售单价为x元.
(1)请直接写出y与x之间的函数关系式和自变量x的取值范围;
(2)当每本足球纪念册销售单价是多少元时,商店每天获利2400元?
(3)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润w元最大?最大利润是多少元?
参考答案
1.解:①由图象知小球在空中达到的最大高度是40m;故①错误;
②小球抛出3秒后,速度越来越快;故②正确;
③小球抛出3秒时达到最高点即速度为0;故③正确;
④设函数解析式为:h=a(t﹣3)2+40,
把O(0,0)代入得0=a(0﹣3)2+40,解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
把h=30代入解析式得,30=﹣(t﹣3)2+40,
解得:t=4.5或t=1.5,
∴小球的高度h=30m时,t=1.5s或4.5s,故④错误;
故选:D.
2.解:
法一:根据题意知,抛物线y=ax2+bx+c(a≠0)经过点(0,54.0)、(40,46.2)、(20,57.9),
则
解得,
所以x=﹣=﹣=15(m).
法二:∵抛物线开口向下,
∴离对称轴越近,位置越高,
从A、C两点来看,对称轴更靠近A,即在20左边,
从A、B两点来看,对称轴更靠近B,即在10右边,
故选:B.
3.解:设窗的高度为xm,宽为()m,
故S=.
∴,
即S=.
∴当x=2m时,S最大值为m2.
故选:C.
4.解:①由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故①错误;
②由图象可知,小球6s时落地,故小球运动的时间为6s,故②正确;
③小球抛出3秒时达到最高点,即速度为0,故③正确;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
∴当t=1.5s时,h=﹣(1.5﹣3)2+40=30,
∴④正确.
综上,正确的有②③④.
故选:C.
5.解:由题意可得,抛物线的顶点坐标为(1,3),
设抛物线的解析式为:y=a(x﹣1)2+3,
2.25=a(0﹣1)2+3,
解得a=﹣0.75,
∴y=﹣(x﹣1)2+3,
当y=0时,﹣(x﹣1)2+3=0,
解得,x1=﹣1,x2=3,
∴点B的坐标为(3,0),
∴OB=3,
答:水流下落点B离墙距离OB的长度是3米.
故选:B.
6.解:∵y=﹣n2+14n﹣24=﹣(n﹣2)(n﹣12),1≤n≤12且n为整数,
∴当y=0时,n=2或n=12,
当y<0时,n=1,
故选:D.
7.解:如图所示:滑行的距离要s与时间t的函数关系可得,当t=6秒时,滑行距离最大,即此时小球停止.
故选:A.
8.解:∵高CH=1cm,BD=2cm,且B、D关于y轴对称,
∴D点坐标为(1,1),
∵AB∥x轴,AB=4cm,最低点C在x轴上,
∴AB关于直线CH对称,
∴左边抛物线的顶点C的坐标为(﹣3,0),
∴右边抛物线的顶点F的坐标为(3,0),
设右边抛物线的解析式为y=a(x﹣3)2,
把D(1,1)代入得1=a×(1﹣3)2,解得a=,
∴右边抛物线的解析式为y=(x﹣3)2,
故选:B.
9.解:∵y=60t﹣t2=﹣(t﹣25)2+750,
∴当t=25时,y取得最大值750,
即飞机着陆后滑行750米才能停下来,
故选:D.
10.解:如右图建立平面直角坐标系,
设抛物线的解析式为y=ax2,
由已知可得,点(2,﹣2)在此抛物线上,
则﹣2=a×22,
解得a=﹣,
∴y=﹣x2,
当y=﹣0.5时,﹣x2=﹣0.5,
解得x=±1,
此时水面的宽度为2m,
故选:B.
11.解:当y=3.05时,﹣x2+3.5=3.05,解得x1=﹣1.5(舍去),x2=1.5,
∴l=2.5+1.5=4m.
故选:B.
12.解:
h=3.5t﹣4.9t2
=﹣4.9(t﹣)2+,
∵﹣4.9<0
∴当t=≈0.36s时,h最大.
故选:D.
13.解:依题意,令h=0得0=20t﹣5t2,
得t(20﹣5t)=0,
解得t=0(舍去)或t=4,
即小球从飞出到落地所用的时间为4s,
故选:B.
14.解:当y=0时,y=﹣x2+x+=0,
解得,x=﹣2(舍去),x=10.
故答案为:10.
15.解:设抛物线的解析式为:y=ax2+b,
由图得知:点(0,2.4),(3,0)在抛物线上,
∴,解得:,
∴抛物线的解析式为:y=﹣x2+2.4,
∵菜农的身高为1.8m,即y=1.8,
则1.8=﹣x2+2.4,
解得:x=±,
故他在不弯腰的情况下,横向活动范围是:3米,
故答案为:3.
16.解:根据题意:y=﹣0.2x2+1.5x﹣2,
当x=﹣=3.75时,y取得最大值,
则最佳加工时间为3.75min.
故答案为:3.75.
17.解:由图形可知,点A(0,21.2)、D(0,1.2)、E(20,9.2)、点F的纵坐标为6.2
设AE所在直线解析式为y=mx+n,
则,
解得:,
∴直线AE解析式为y=﹣0.6x+21.2,
当y=6.2时,﹣0.6x+21.2=6.2,
解得:x=25,
∴点F坐标为(25,6.2),
设抛物线的解析式为y=ax2+bx+c,
将点D(0,1.2)、E(20,9.2)、F(25,6.2)代入,得:
,
解得:,
∴抛物线的解析式为y=﹣x2+x+=﹣(x﹣15)2+,
设消防员向左移动的距离为p(p>0),
则移动后抛物线的解析式为y=﹣(x+p﹣15)2++,
根据题意知,平移后抛物线过点F(25,6.2),代入得:
﹣(25+p﹣15)2++=6.2,
解得:p=﹣﹣10(舍)或p=﹣10,
即消防员将水流抛物线向上平移0.4m,再向左后退了(﹣10)m,恰好把水喷到F处进行灭火,
故答案为:﹣10.
18.解:∵a=﹣1.5<0,
∴函数有最大值.
∴y最大值===600,
即飞机着陆后滑行600米才能停止.
故答案为:600.
19.解:如图所示:
设在6分钟时到达A点,在14分钟时到达B,
∵6分钟时和14分钟时拱梁的高度相同,
∴A,B关于对称轴对称.则从A到B需要8分钟,则从A到D需要4分钟.
∴从O到D需要6+4=10(分钟).
∴从O到C需要2×10=20(分钟).
故答案为20.
20.解:以池中心A为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.
抛物线的解析式为:y=﹣(x﹣1)2+3,
当选取点D为坐标原点时,相当于将原图象向左平移3个单位,
故平移后的抛物线表达式为:y=﹣(x+2)2+3(﹣3≤x≤0);
令x=﹣3,则y=﹣+3=2.25.
故水管AB的长为2.25m.
故答案为:y=﹣(x+2)2+3(﹣3≤x≤0);2.25.
21.解:如图,
∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE 面积的2倍,
∴AE=2BE,
设 BC=x(m),BE=FC=a(m),则AE=HG=DF=2a(m),
∴DF+FC+HG+AE+EB+EF+BC=60(m),即 8a+2x=60,
∴a=﹣x+,3a=﹣x+,
∴矩形区域 ABCD 的面积 S=(﹣x+)x=﹣x2+x,
∵a=﹣x+
∴x<30,
则 S=﹣x2+x (0<x<30)
∵二次项系数为﹣<0
∴当x=﹣=15(m)时,S 有最大值,最大值为:﹣×152+×15=(m2)
故答案为:15m.
22.解:(1)由题意得,y=700﹣20(x﹣45)=﹣20x+1600(45≤x≤80 );
(2)P=(x﹣40)(﹣20x+1600)=﹣20x2+2400x﹣64000=﹣20(x﹣60)2+8000,
∵x≥45,a=﹣20<0,
∴当x=60时,P最大值=8000元,
即当每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元;
(3)由题意,得﹣20(x﹣60)2+8000=6000,
解得x1=50,x2=70.
∵抛物线P=﹣20(x﹣60)2+8000的开口向下,
∴当50≤x≤70时,每天销售粽子的利润不低于6000元的利润.
又∵x≤58,
∴50≤x≤58.
∵在y=﹣20x+1600中,k=﹣20<0,
∴y随x的增大而减小,
∴当x=58时,y最小值=﹣20×58+1600=440,
即超市每天至少销售粽子440盒.
23.解:(1)设y=kx+b,
∵直线y=kx+b经过点(40,300),(55,150),
∴,
解得:.
故y与x之间的函数关系式为:y=﹣10x+700,
(2)由题意,得
﹣10x+700≥240,
解得x≤46,
∴30<x≤46,
设利润为w=(x﹣30) y=(x﹣30)(﹣10x+700),
w=﹣10x2+1000x﹣21000=﹣10(x﹣50)2+4000,
∵﹣10<0,
∴x<50时,w随x的增大而增大,
∴x=46时,w最大=﹣10(46﹣50)2+4000=3840,
答:当销售单价为46元时,每天获取的利润最大,最大利润是3840元;
(3)w﹣150=﹣10x2+1000x﹣21000﹣150=3600,
﹣10(x﹣50)2=﹣250,
x﹣50=±5,
x1=55,x2=45,
如图所示,由图象得:
当45≤x≤55时,捐款后每天剩余利润不低于3600元.
24.解:(1)∵AB=x,则BC=(28﹣x),
∴x(28﹣x)=192,
解得:x1=12,x2=16,
答:x的值为12或16;
(2)∵AB=xm,
∴BC=28﹣x,
∴S=x(28﹣x)=﹣x2+28x=﹣(x﹣14)2+196,
∵在P处有一棵树与墙CD,AD的距离分别是15m和6m,
∵28﹣15=13,
∴6≤x≤13,
∴当x=13时,S取到最大值为:S=﹣(13﹣14)2+196=195,
答:花园面积S的最大值为195平方米.
25.解:(1)y=,
(2)在0≤x≤10时,y=100x,当x=10时,y有最大值1000;
在10<x≤30时,y=﹣3x2+130x,
当x=21时,y取得最大值,
∵x为整数,根据抛物线的对称性得x=22时,y有最大值1408.
∵1408>1000,
∴顾客一次购买22件时,该网站从中获利最多.
26.解:(1)y=300﹣10(x﹣44),
即y=﹣10x+740(44≤x≤52);
(2)根据题意得(x﹣40)(﹣10x+740)=2400,
解得x1=50,x2=64(舍去),
答:当每本足球纪念册销售单价是50元时,商店每天获利2400元;
(3)w=(x﹣40)(﹣10x+740)
=﹣10x2+1140x﹣29600
=﹣10(x﹣57)2+2890,
当x<57时,w随x的增大而增大,
而44≤x≤52,
所以当x=52时,w有最大值,最大值为﹣10(52﹣57)2+2890=2640,
答:将足球纪念册销售单价定为52元时,商店每天销售纪念册获得的利润w最大,最大利润是2640元.
1.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球抛出3秒后,速度越来越快;
③小球抛出3秒时速度为0;
④小球的高度h=30m时,t=1.5s.
其中正确的是( )
A.①④ B.①② C.②③④ D.②③
2.跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )
A.10m B.15m C.20m D.22.5m
3.用长8m的铝合金条制成如图形状的矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是( )
A.m2 B.m2 C.m2 D.4m2
4.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④ B.①② C.②③④ D.②④
5.如图,某幢建筑物从2.25米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )
A.2.5米 B.3米 C.3.5米 D.4米
6.黄山市某塑料玩具生产公司,为了减少空气污染,国家要求限制塑料玩具生产,这样有时企业会被迫停产,经过调研预测,它一年中每月获得的利润y(万元)和月份n之间满足函数关系式y=﹣n2+14n﹣24,则没有盈利的月份为( )
A.2月和12月 B.2月至12月
C.1月 D.1月、2月和12月
7.地面上一个小球被推开后笔直滑行,滑行的距离s与时间t的函数关系如图中的部分抛物线所示(其中P是该抛物线的顶点),则下列说法正确的是( )
A.小球滑行6秒停止 B.小球滑行12秒停止
C.小球滑行6秒回到起点 D.小球滑行12秒回到起点
8.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )
A.y=(x+3)2 B.y=(x﹣3)2
C.y=﹣(x+3)2 D.y=﹣(x﹣3)2
9.飞机着陆后滑行的距离y(单位:m)与滑行时间t(单位:s)的函数关系式满足y=﹣t2+60t,则飞机着陆至停下来滑行的距离是( )
A.25m B.50m C.625m D.750m
10.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面上升1.5m,水面宽度为( )
A.1m B.2m C.m D.m
11.小敏在某次投篮中,球的运动线路是抛物线y=﹣x2+3.5的一部分(如图),若命中篮圈中心,则他与篮底的距离l是( )
A.3.5m B.4m C.4.5m D.4.6m
12.小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数h=3.5t﹣4.9t2(t的单位:s,h的单位:m)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
A.0.71s B.0.70s C.0.63s D.0.36s
13.如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为h=20t﹣5t2,则小球从飞出到落地的所用时间为( )
A.3s B.4s C.5s D.6s
14.在广安市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=﹣x2+x+,由此可知该生此次实心球训练的成绩为 米.
15.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8m,他在不弯腰的情况下,在棚内的横向活动范围是 m.
16.加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率y与加工时间x(单位:min)满足函数表达式y=﹣0.2x2+1.5x﹣2,则最佳加工时间为 min.
17.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了 m,恰好把水喷到F处进行灭火.
18.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2,该型号飞机着陆后滑行 m才能停下来.
19.如图,某大桥有一段抛物线形的拱梁,抛物线的解析式为y=ax2+bx,小强骑自行车从拱梁一端O匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶到6分钟和14分钟时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需 分钟.
20.如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端安有一个喷水池,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m,水柱落地点D离池中心A处3m,以水平方向为x轴,建立平面直角坐标系,若选取A点为坐标原点时的抛物线的表达式为y=﹣,则选取点D为坐标原点时的抛物线表达式为 ,水管AB的长为 m.
21.为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为60m的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则BC长为 时,能围成的矩形区域ABCD的面积最大.
22.为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
23.“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,如图所示.
(1)求y与x之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
24.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
25.某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
26.俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为y本,销售单价为x元.
(1)请直接写出y与x之间的函数关系式和自变量x的取值范围;
(2)当每本足球纪念册销售单价是多少元时,商店每天获利2400元?
(3)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润w元最大?最大利润是多少元?
参考答案
1.解:①由图象知小球在空中达到的最大高度是40m;故①错误;
②小球抛出3秒后,速度越来越快;故②正确;
③小球抛出3秒时达到最高点即速度为0;故③正确;
④设函数解析式为:h=a(t﹣3)2+40,
把O(0,0)代入得0=a(0﹣3)2+40,解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
把h=30代入解析式得,30=﹣(t﹣3)2+40,
解得:t=4.5或t=1.5,
∴小球的高度h=30m时,t=1.5s或4.5s,故④错误;
故选:D.
2.解:
法一:根据题意知,抛物线y=ax2+bx+c(a≠0)经过点(0,54.0)、(40,46.2)、(20,57.9),
则
解得,
所以x=﹣=﹣=15(m).
法二:∵抛物线开口向下,
∴离对称轴越近,位置越高,
从A、C两点来看,对称轴更靠近A,即在20左边,
从A、B两点来看,对称轴更靠近B,即在10右边,
故选:B.
3.解:设窗的高度为xm,宽为()m,
故S=.
∴,
即S=.
∴当x=2m时,S最大值为m2.
故选:C.
4.解:①由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故①错误;
②由图象可知,小球6s时落地,故小球运动的时间为6s,故②正确;
③小球抛出3秒时达到最高点,即速度为0,故③正确;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
∴当t=1.5s时,h=﹣(1.5﹣3)2+40=30,
∴④正确.
综上,正确的有②③④.
故选:C.
5.解:由题意可得,抛物线的顶点坐标为(1,3),
设抛物线的解析式为:y=a(x﹣1)2+3,
2.25=a(0﹣1)2+3,
解得a=﹣0.75,
∴y=﹣(x﹣1)2+3,
当y=0时,﹣(x﹣1)2+3=0,
解得,x1=﹣1,x2=3,
∴点B的坐标为(3,0),
∴OB=3,
答:水流下落点B离墙距离OB的长度是3米.
故选:B.
6.解:∵y=﹣n2+14n﹣24=﹣(n﹣2)(n﹣12),1≤n≤12且n为整数,
∴当y=0时,n=2或n=12,
当y<0时,n=1,
故选:D.
7.解:如图所示:滑行的距离要s与时间t的函数关系可得,当t=6秒时,滑行距离最大,即此时小球停止.
故选:A.
8.解:∵高CH=1cm,BD=2cm,且B、D关于y轴对称,
∴D点坐标为(1,1),
∵AB∥x轴,AB=4cm,最低点C在x轴上,
∴AB关于直线CH对称,
∴左边抛物线的顶点C的坐标为(﹣3,0),
∴右边抛物线的顶点F的坐标为(3,0),
设右边抛物线的解析式为y=a(x﹣3)2,
把D(1,1)代入得1=a×(1﹣3)2,解得a=,
∴右边抛物线的解析式为y=(x﹣3)2,
故选:B.
9.解:∵y=60t﹣t2=﹣(t﹣25)2+750,
∴当t=25时,y取得最大值750,
即飞机着陆后滑行750米才能停下来,
故选:D.
10.解:如右图建立平面直角坐标系,
设抛物线的解析式为y=ax2,
由已知可得,点(2,﹣2)在此抛物线上,
则﹣2=a×22,
解得a=﹣,
∴y=﹣x2,
当y=﹣0.5时,﹣x2=﹣0.5,
解得x=±1,
此时水面的宽度为2m,
故选:B.
11.解:当y=3.05时,﹣x2+3.5=3.05,解得x1=﹣1.5(舍去),x2=1.5,
∴l=2.5+1.5=4m.
故选:B.
12.解:
h=3.5t﹣4.9t2
=﹣4.9(t﹣)2+,
∵﹣4.9<0
∴当t=≈0.36s时,h最大.
故选:D.
13.解:依题意,令h=0得0=20t﹣5t2,
得t(20﹣5t)=0,
解得t=0(舍去)或t=4,
即小球从飞出到落地所用的时间为4s,
故选:B.
14.解:当y=0时,y=﹣x2+x+=0,
解得,x=﹣2(舍去),x=10.
故答案为:10.
15.解:设抛物线的解析式为:y=ax2+b,
由图得知:点(0,2.4),(3,0)在抛物线上,
∴,解得:,
∴抛物线的解析式为:y=﹣x2+2.4,
∵菜农的身高为1.8m,即y=1.8,
则1.8=﹣x2+2.4,
解得:x=±,
故他在不弯腰的情况下,横向活动范围是:3米,
故答案为:3.
16.解:根据题意:y=﹣0.2x2+1.5x﹣2,
当x=﹣=3.75时,y取得最大值,
则最佳加工时间为3.75min.
故答案为:3.75.
17.解:由图形可知,点A(0,21.2)、D(0,1.2)、E(20,9.2)、点F的纵坐标为6.2
设AE所在直线解析式为y=mx+n,
则,
解得:,
∴直线AE解析式为y=﹣0.6x+21.2,
当y=6.2时,﹣0.6x+21.2=6.2,
解得:x=25,
∴点F坐标为(25,6.2),
设抛物线的解析式为y=ax2+bx+c,
将点D(0,1.2)、E(20,9.2)、F(25,6.2)代入,得:
,
解得:,
∴抛物线的解析式为y=﹣x2+x+=﹣(x﹣15)2+,
设消防员向左移动的距离为p(p>0),
则移动后抛物线的解析式为y=﹣(x+p﹣15)2++,
根据题意知,平移后抛物线过点F(25,6.2),代入得:
﹣(25+p﹣15)2++=6.2,
解得:p=﹣﹣10(舍)或p=﹣10,
即消防员将水流抛物线向上平移0.4m,再向左后退了(﹣10)m,恰好把水喷到F处进行灭火,
故答案为:﹣10.
18.解:∵a=﹣1.5<0,
∴函数有最大值.
∴y最大值===600,
即飞机着陆后滑行600米才能停止.
故答案为:600.
19.解:如图所示:
设在6分钟时到达A点,在14分钟时到达B,
∵6分钟时和14分钟时拱梁的高度相同,
∴A,B关于对称轴对称.则从A到B需要8分钟,则从A到D需要4分钟.
∴从O到D需要6+4=10(分钟).
∴从O到C需要2×10=20(分钟).
故答案为20.
20.解:以池中心A为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.
抛物线的解析式为:y=﹣(x﹣1)2+3,
当选取点D为坐标原点时,相当于将原图象向左平移3个单位,
故平移后的抛物线表达式为:y=﹣(x+2)2+3(﹣3≤x≤0);
令x=﹣3,则y=﹣+3=2.25.
故水管AB的长为2.25m.
故答案为:y=﹣(x+2)2+3(﹣3≤x≤0);2.25.
21.解:如图,
∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE 面积的2倍,
∴AE=2BE,
设 BC=x(m),BE=FC=a(m),则AE=HG=DF=2a(m),
∴DF+FC+HG+AE+EB+EF+BC=60(m),即 8a+2x=60,
∴a=﹣x+,3a=﹣x+,
∴矩形区域 ABCD 的面积 S=(﹣x+)x=﹣x2+x,
∵a=﹣x+
∴x<30,
则 S=﹣x2+x (0<x<30)
∵二次项系数为﹣<0
∴当x=﹣=15(m)时,S 有最大值,最大值为:﹣×152+×15=(m2)
故答案为:15m.
22.解:(1)由题意得,y=700﹣20(x﹣45)=﹣20x+1600(45≤x≤80 );
(2)P=(x﹣40)(﹣20x+1600)=﹣20x2+2400x﹣64000=﹣20(x﹣60)2+8000,
∵x≥45,a=﹣20<0,
∴当x=60时,P最大值=8000元,
即当每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元;
(3)由题意,得﹣20(x﹣60)2+8000=6000,
解得x1=50,x2=70.
∵抛物线P=﹣20(x﹣60)2+8000的开口向下,
∴当50≤x≤70时,每天销售粽子的利润不低于6000元的利润.
又∵x≤58,
∴50≤x≤58.
∵在y=﹣20x+1600中,k=﹣20<0,
∴y随x的增大而减小,
∴当x=58时,y最小值=﹣20×58+1600=440,
即超市每天至少销售粽子440盒.
23.解:(1)设y=kx+b,
∵直线y=kx+b经过点(40,300),(55,150),
∴,
解得:.
故y与x之间的函数关系式为:y=﹣10x+700,
(2)由题意,得
﹣10x+700≥240,
解得x≤46,
∴30<x≤46,
设利润为w=(x﹣30) y=(x﹣30)(﹣10x+700),
w=﹣10x2+1000x﹣21000=﹣10(x﹣50)2+4000,
∵﹣10<0,
∴x<50时,w随x的增大而增大,
∴x=46时,w最大=﹣10(46﹣50)2+4000=3840,
答:当销售单价为46元时,每天获取的利润最大,最大利润是3840元;
(3)w﹣150=﹣10x2+1000x﹣21000﹣150=3600,
﹣10(x﹣50)2=﹣250,
x﹣50=±5,
x1=55,x2=45,
如图所示,由图象得:
当45≤x≤55时,捐款后每天剩余利润不低于3600元.
24.解:(1)∵AB=x,则BC=(28﹣x),
∴x(28﹣x)=192,
解得:x1=12,x2=16,
答:x的值为12或16;
(2)∵AB=xm,
∴BC=28﹣x,
∴S=x(28﹣x)=﹣x2+28x=﹣(x﹣14)2+196,
∵在P处有一棵树与墙CD,AD的距离分别是15m和6m,
∵28﹣15=13,
∴6≤x≤13,
∴当x=13时,S取到最大值为:S=﹣(13﹣14)2+196=195,
答:花园面积S的最大值为195平方米.
25.解:(1)y=,
(2)在0≤x≤10时,y=100x,当x=10时,y有最大值1000;
在10<x≤30时,y=﹣3x2+130x,
当x=21时,y取得最大值,
∵x为整数,根据抛物线的对称性得x=22时,y有最大值1408.
∵1408>1000,
∴顾客一次购买22件时,该网站从中获利最多.
26.解:(1)y=300﹣10(x﹣44),
即y=﹣10x+740(44≤x≤52);
(2)根据题意得(x﹣40)(﹣10x+740)=2400,
解得x1=50,x2=64(舍去),
答:当每本足球纪念册销售单价是50元时,商店每天获利2400元;
(3)w=(x﹣40)(﹣10x+740)
=﹣10x2+1140x﹣29600
=﹣10(x﹣57)2+2890,
当x<57时,w随x的增大而增大,
而44≤x≤52,
所以当x=52时,w有最大值,最大值为﹣10(52﹣57)2+2890=2640,
答:将足球纪念册销售单价定为52元时,商店每天销售纪念册获得的利润w最大,最大利润是2640元.
