2021-2022学年湘教版八年级数学上册第二章 三角形 单元测试卷 (Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学上册第二章 三角形 单元测试卷 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 235.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 10:29:15 | ||
图片预览




文档简介
第二章三角形单元测试卷 2021-2022学年湘教版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
如图,共有三角形( )
A. 个 B. 个
C. 个 D. 个
下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
下列图形中AD是三角形ABC的高线的是( )
A. B.
C. D.
下列选项中,可以用来说明命题“两个锐角的和是钝角”是假命题的是( )
A. , B. ,
C. , D. ,
三角形的一个外角小于与它相邻的内角,这个三角形是( )
A. 直角三角形 B. 钝角三角形 C. 锐角三角形 D. 不确定
若ABCDEF,且ABC的周长为20,AB=5,BC=8,则DF的长为( )
A. B. C. D. 或
如图,在ABC中,B=,C=,AD平分BAC交BC于D,DEAB,交AC于E,则ADE的大小是( )
A. B.
C. D.
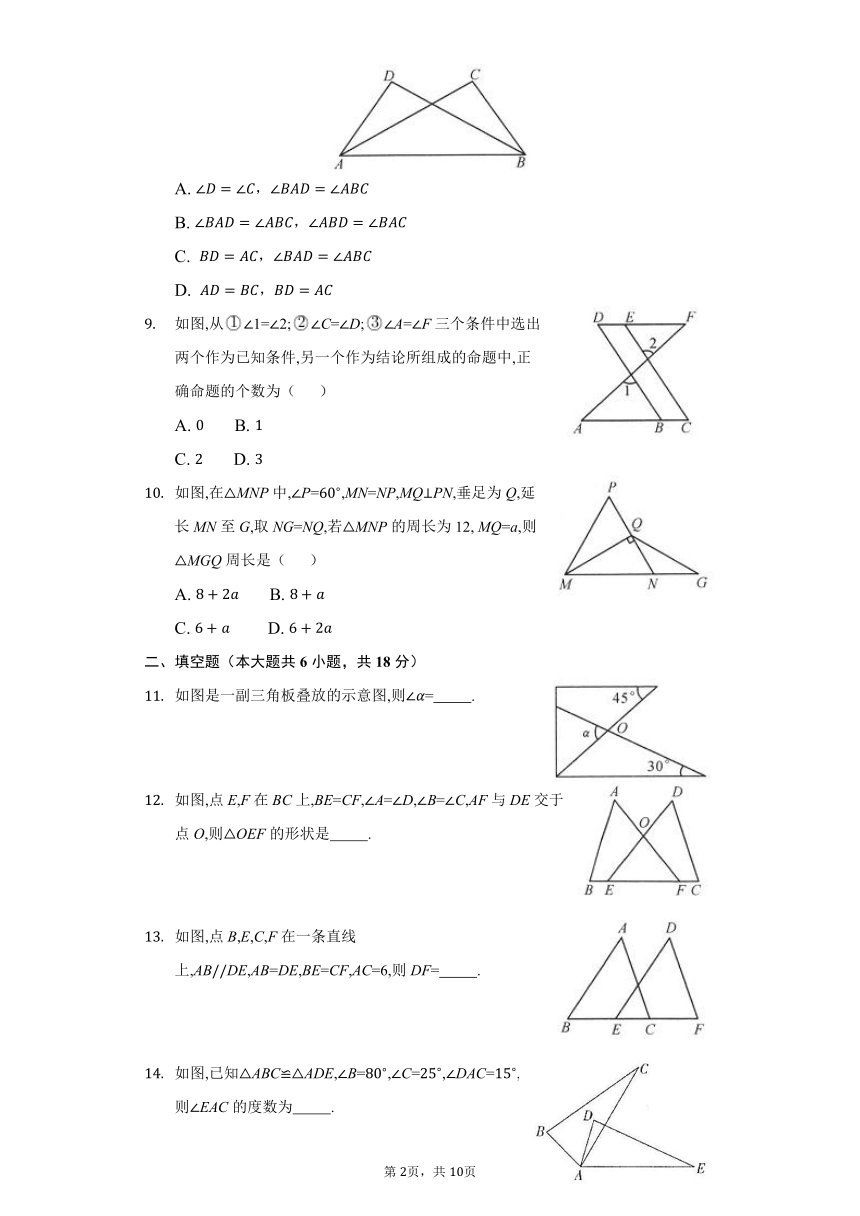
如图,在下列条件中,不能判断ABDBAC的是( )
A. ,
B. ,
C. ,
D. ,
如图,从1=2;C=D;A=F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
A. B.
C. D.
如图,在MNP中,P=,MN=NP,MQPN,垂足为Q,延长MN至G,取NG=NQ,若MNP的周长为12, MQ=a,则MGQ周长是( )
A. B.
C. D.
二、填空题(本大题共6小题,共18分)
如图是一副三角板叠放的示意图,则= .
如图,点E,F在BC上,BE=CF,A=D,B=C,AF与DE交于点O,则OEF的形状是 .
如图,点B,E,C,F在一条直线上,ABDE,AB=DE,BE=CF,AC=6,则DF= .
如图,已知ABCADE,B=,C=,DAC=,则EAC的度数为 .
如图,直线,点A在直线上,点B在直线上,AB=BC,C=,1=,则2= .
如图,在ABC中,A=,ABC和ACD的平分线交于点,得;和的平分线交于点,得;,和的平分线交于点,则= .
三、解答题(本大题共7小题,共72分)
尺规作图:如图,已知线段a和AOB,点M在OB上.(不写作法,保留作图痕迹)
(1)在OA边上作点P,使OP=2a;
(2)作AOB的平分线;
(3)过点M作OB的垂线.
如图,已知ABCD,1=F,2=E,试猜想AF与DE的位置关系,并证明你的结论.
如图,在ABC中,AB=AC,BD平分ABC交AC于点D,BEBD,DEBC,BE与DE交于点E,DE交AB于点F.
(1)若A=,求E的度数;
(2)求证:BF=EF.
已知ABN和ACM的位置如图所示,AB=AC,AD=AE,1=2.求证:
(1)BD=CE;
(2)M=N.
求证:顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半.(1)在图中按照下面“已知”的要求,画出符合题意的图形,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.
已知:在ABC中,AB=AC, .
求证: .
(2)证明上述命题.
如图,在等腰直角三角形ABC中,ACB=,D是斜边AB上任一点,AECD于E,BFCD交CD的延长线于F,CHAB于H,交AE于G.
求证:(1)AE=EF+BF;
(2)CG=BD.
23.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 ;(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
请找出图中与BE相等的线段,并说明理由;
直接写出线段BE长的最大值.
1.【答案】A
2.【答案】D
3.【答案】D
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】
12.【答案】等腰三角形
13.【答案】6
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】解:AFDE.
证明:ABCD,
2=EGB.
GBE=1+F,E+EGB+GBE=,
E+2+1+F=.
又1=F,2=E,
F+E=.
AFDE.
19.【答案】(1)解:AB=AC,A=,
ABC=ACB=(-)=,
BD平分ABC,
DBF=DBC=ABC=,
DEBC,
EDB=DBC=,
BEBD,
DBE=,
E=--=.
(2)证明:BD平分ABC,
DBF=DBC,
DEBC,
EDB=DBC,
BEBD,
EBF+DBF=E+BDE=,
E=EBF,
BF=EF.
20.【答案】证明:(1)在ABD和ACE中,
∴△ABD△ACE(SAS).
∴BD=CE.
(2)∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,
即∠BAN=∠CAM.
由(1)得ABDACE,
B=C.
在ACM和ABN中,
∴ACMABN(ASA).
∴M=N.
21.【答案】解:(1)CDAB于点D , BCD=A
(2)证明:AB=AC,
B=ACB=(-A)=-A.
CDAB,
ACD=-A.
BCD=ACB-ACD=(-A)-(-A)=A.
22.【答案】证明:(1)ACB=,
即ACE+BCF=.
又BFCD于F,
BCF+CBF=.
ACE=CBF.
又AECD于E,BFCD于F.
AEC=CFB=.
ACB是等腰直角三角形,且ACB=,
AC=CB.
在ACE与CBF中,
ACECBF(AAS).
AE=CF,CE=BF.
CF=CE+EF=BF+EF=AE,即AE=EF+BF.
(2)证法一:CHAB于H,
CDH+DCH=,又BDF+FBD=,且CDH=BDF,
ECG=FBD.
由(1)知,CE=BF.
在CEG与BFD中,
CEGBFD(ASA),
CG=BD.
证法二:CH是等腰直角三角形ABC斜边上的高线,
ACG=.
又CBA=CAB=,
ACG=CBD.
由(1)知,ACECBF,
CAG=BCD.
在ACG与CBD中,
ACGCBD(ASA),
CG=BD.
23.【答案】解:(1)CB的延长线上, a+b
(2)CD=BE.
理由:ABD和ACE是等边三角形,
AD=AB,AC=AE,BAD=CAE=
BAD+BAC=CAE+BAC,即CAD=EAB.
在CAD和EAB中,
CADEAB(SAS).
CD=BE.
线段BE长的最大值为4.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
如图,共有三角形( )
A. 个 B. 个
C. 个 D. 个
下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
下列图形中AD是三角形ABC的高线的是( )
A. B.
C. D.
下列选项中,可以用来说明命题“两个锐角的和是钝角”是假命题的是( )
A. , B. ,
C. , D. ,
三角形的一个外角小于与它相邻的内角,这个三角形是( )
A. 直角三角形 B. 钝角三角形 C. 锐角三角形 D. 不确定
若ABCDEF,且ABC的周长为20,AB=5,BC=8,则DF的长为( )
A. B. C. D. 或
如图,在ABC中,B=,C=,AD平分BAC交BC于D,DEAB,交AC于E,则ADE的大小是( )
A. B.
C. D.
如图,在下列条件中,不能判断ABDBAC的是( )
A. ,
B. ,
C. ,
D. ,
如图,从1=2;C=D;A=F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
A. B.
C. D.
如图,在MNP中,P=,MN=NP,MQPN,垂足为Q,延长MN至G,取NG=NQ,若MNP的周长为12, MQ=a,则MGQ周长是( )
A. B.
C. D.
二、填空题(本大题共6小题,共18分)
如图是一副三角板叠放的示意图,则= .
如图,点E,F在BC上,BE=CF,A=D,B=C,AF与DE交于点O,则OEF的形状是 .
如图,点B,E,C,F在一条直线上,ABDE,AB=DE,BE=CF,AC=6,则DF= .
如图,已知ABCADE,B=,C=,DAC=,则EAC的度数为 .
如图,直线,点A在直线上,点B在直线上,AB=BC,C=,1=,则2= .
如图,在ABC中,A=,ABC和ACD的平分线交于点,得;和的平分线交于点,得;,和的平分线交于点,则= .
三、解答题(本大题共7小题,共72分)
尺规作图:如图,已知线段a和AOB,点M在OB上.(不写作法,保留作图痕迹)
(1)在OA边上作点P,使OP=2a;
(2)作AOB的平分线;
(3)过点M作OB的垂线.
如图,已知ABCD,1=F,2=E,试猜想AF与DE的位置关系,并证明你的结论.
如图,在ABC中,AB=AC,BD平分ABC交AC于点D,BEBD,DEBC,BE与DE交于点E,DE交AB于点F.
(1)若A=,求E的度数;
(2)求证:BF=EF.
已知ABN和ACM的位置如图所示,AB=AC,AD=AE,1=2.求证:
(1)BD=CE;
(2)M=N.
求证:顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半.(1)在图中按照下面“已知”的要求,画出符合题意的图形,并根据题设和结论,结合图形,用符号语言补充写出“已知”和“求证”.
已知:在ABC中,AB=AC, .
求证: .
(2)证明上述命题.
如图,在等腰直角三角形ABC中,ACB=,D是斜边AB上任一点,AECD于E,BFCD交CD的延长线于F,CHAB于H,交AE于G.
求证:(1)AE=EF+BF;
(2)CG=BD.
23.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 ;(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
请找出图中与BE相等的线段,并说明理由;
直接写出线段BE长的最大值.
1.【答案】A
2.【答案】D
3.【答案】D
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】
12.【答案】等腰三角形
13.【答案】6
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】解:AFDE.
证明:ABCD,
2=EGB.
GBE=1+F,E+EGB+GBE=,
E+2+1+F=.
又1=F,2=E,
F+E=.
AFDE.
19.【答案】(1)解:AB=AC,A=,
ABC=ACB=(-)=,
BD平分ABC,
DBF=DBC=ABC=,
DEBC,
EDB=DBC=,
BEBD,
DBE=,
E=--=.
(2)证明:BD平分ABC,
DBF=DBC,
DEBC,
EDB=DBC,
BEBD,
EBF+DBF=E+BDE=,
E=EBF,
BF=EF.
20.【答案】证明:(1)在ABD和ACE中,
∴△ABD△ACE(SAS).
∴BD=CE.
(2)∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,
即∠BAN=∠CAM.
由(1)得ABDACE,
B=C.
在ACM和ABN中,
∴ACMABN(ASA).
∴M=N.
21.【答案】解:(1)CDAB于点D , BCD=A
(2)证明:AB=AC,
B=ACB=(-A)=-A.
CDAB,
ACD=-A.
BCD=ACB-ACD=(-A)-(-A)=A.
22.【答案】证明:(1)ACB=,
即ACE+BCF=.
又BFCD于F,
BCF+CBF=.
ACE=CBF.
又AECD于E,BFCD于F.
AEC=CFB=.
ACB是等腰直角三角形,且ACB=,
AC=CB.
在ACE与CBF中,
ACECBF(AAS).
AE=CF,CE=BF.
CF=CE+EF=BF+EF=AE,即AE=EF+BF.
(2)证法一:CHAB于H,
CDH+DCH=,又BDF+FBD=,且CDH=BDF,
ECG=FBD.
由(1)知,CE=BF.
在CEG与BFD中,
CEGBFD(ASA),
CG=BD.
证法二:CH是等腰直角三角形ABC斜边上的高线,
ACG=.
又CBA=CAB=,
ACG=CBD.
由(1)知,ACECBF,
CAG=BCD.
在ACG与CBD中,
ACGCBD(ASA),
CG=BD.
23.【答案】解:(1)CB的延长线上, a+b
(2)CD=BE.
理由:ABD和ACE是等边三角形,
AD=AB,AC=AE,BAD=CAE=
BAD+BAC=CAE+BAC,即CAD=EAB.
在CAD和EAB中,
CADEAB(SAS).
CD=BE.
线段BE长的最大值为4.
第2页,共3页
同课章节目录
