2021—2022学年鲁教版(五四制)数学九年级下册6.1用树状图或表格求概率 课件(25张)
文档属性
| 名称 | 2021—2022学年鲁教版(五四制)数学九年级下册6.1用树状图或表格求概率 课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 10:37:01 | ||
图片预览








文档简介
(共25张PPT)
6.1用树状图或表格求概率
第六章对概率的进一步认识
1.下列事件中,属于随机事件的是( )
A.抛出的篮球会下落
B.从装有黑球、白球的袋中摸出红球
C.367人中有2人是同月同日出生
D.买一张彩票,中500万大奖
知识复习1:
2.某种彩票的中奖机会是1%,下列说法正确的是( )
A.买1张这种彩票一定不会中奖
B.买1张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定在1%
4.一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是( )
A.m=3,n=5 B.m=n=4 C.m+n=4 D.m+n=8
3.从1, 2 , 3 , 4 , 5 , 6 , 7 , 8 ,9 , 10 这十个数中随机取出一个数,取出的数是是3的倍数的概率是 .
5.抛掷一枚硬币出现反面朝上的概率是 .
正面朝上的概率是____________
若抛掷两枚硬币,一正,一反发生的概率又是多少呢
问题思考:
1.事件的分类
确定事件:确定事件包括必然事件与不可能事件;
必然事件:在一定条件下,一定会发生的事件;
不可能事件:在一定条件下一定不会发生的事件;
随机事件:在一定条件下,可能______,也可能________的事件叫做不确定事件,称为随机事件.
知识复习2:
2.概率的概念
概率定义:把事件A发生可能性大小称为事件A发生的概率,记为P(A).
各类事件的概率:必然事件发生的概率为_____,不可能事件发生的概率为_____ ,随机事件发生的概率介于_____与_____之间.
3.有6张卡片,每张卡片上分别写有不同的从1到6的一个自然数,从中任意抽出一张卡片,卡片上的数是3的倍数的概率是______.
4.甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为_____.
你是怎样求出以上概率的?思考下列问题
若抛掷两枚硬币,一正,一反发生的概率又是多少呢
本节课学习目标:
1.理解为什么要列树状图或表格;
2.能熟练用画树状图或列表格的方法求不确定事件的概率.
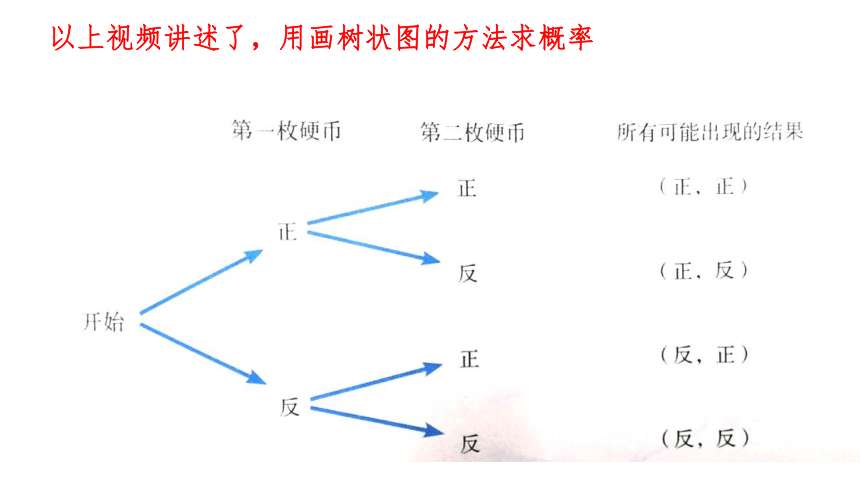
以上视频讲述了,用画树状图的方法求概率
怎样用列表的方法,求概率呢?
第二枚硬币 第一枚硬币 正 反
正 (正,正) (正,反)
反 (反,正) (反,反)
共有4种情况,小明获胜的结果有一种,小明获胜的概率P(小明胜)=
小颖获胜的结果有一种,小颖获胜的概率P(小颖胜)=
小凡获胜的结果有一种,小凡获胜的概率P(小凡胜)=
例题学习1:
例1,在A、B两个盒子中都装入分别写有数字1、2的两张卡片,分别从每个盒子中任意取出一张卡片,两张卡片上的数字之和为3的概率是多少?
B盒 A盒 1 2
1 (1,1) (1,2)
2 (2,1) (2,2)
随堂练习:
例题学习2:
例2,小明,小颖,小凡做“石头、剪刀、布”的游戏,游戏规则如下:
由小明和小颖玩“石头、剪刀、布”的游戏如果两人的手势相同,那么小凡获胜;
如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的胜者。假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?
随堂练习:
3.小亮从语文、数学、英语3本课本中任意抽取一本,又从这3门课的作业中任意抽取一本,课本和作业恰好为同一门课的概率是多少?
4、小明和小军作掷骰子游戏,两人各掷一枚均匀的骰子。
(1)若两人掷得点数之和为奇数,则小军获胜,否则小明获胜,这个游戏对双方公平吗?为什么?
(2)若两人掷得点数之和为奇数,则小军获胜,否则小明获胜,这个游戏对双方公平吗?为什么?
课堂小结:
1、用画树状图或列表的方法求概率
2、画树状图与列表有什么优点?说说你的想法。
集中练习:
C
中考题欣赏1:
1、某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
(1)本次问卷调查共调查了________名观众;图②中最喜爱“体育节目”的扇形圆心角度数是________.
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为A),“体育节目”(记为B),“综艺节目”(记为C),“科普节目”(记为D)的观众各一名,电视台要从四人中随机抽取
两人参加联谊活动,请用列表或画树状图的方法,
求出恰好抽到最喜爱“B”和“C”两位观众的概率.
中考题欣赏2:
2.某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
根据图中信息解决下列问题:
(1)本次共调查 名学生,扇形统计图中B所对应的扇形的圆心角为 度;
(2)补全条形统计图;
(3)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
6.1用树状图或表格求概率
第六章对概率的进一步认识
1.下列事件中,属于随机事件的是( )
A.抛出的篮球会下落
B.从装有黑球、白球的袋中摸出红球
C.367人中有2人是同月同日出生
D.买一张彩票,中500万大奖
知识复习1:
2.某种彩票的中奖机会是1%,下列说法正确的是( )
A.买1张这种彩票一定不会中奖
B.买1张这种彩票一定会中奖
C.买100张这种彩票一定会中奖
D.当购买彩票的数量很大时,中奖的频率稳定在1%
4.一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是( )
A.m=3,n=5 B.m=n=4 C.m+n=4 D.m+n=8
3.从1, 2 , 3 , 4 , 5 , 6 , 7 , 8 ,9 , 10 这十个数中随机取出一个数,取出的数是是3的倍数的概率是 .
5.抛掷一枚硬币出现反面朝上的概率是 .
正面朝上的概率是____________
若抛掷两枚硬币,一正,一反发生的概率又是多少呢
问题思考:
1.事件的分类
确定事件:确定事件包括必然事件与不可能事件;
必然事件:在一定条件下,一定会发生的事件;
不可能事件:在一定条件下一定不会发生的事件;
随机事件:在一定条件下,可能______,也可能________的事件叫做不确定事件,称为随机事件.
知识复习2:
2.概率的概念
概率定义:把事件A发生可能性大小称为事件A发生的概率,记为P(A).
各类事件的概率:必然事件发生的概率为_____,不可能事件发生的概率为_____ ,随机事件发生的概率介于_____与_____之间.
3.有6张卡片,每张卡片上分别写有不同的从1到6的一个自然数,从中任意抽出一张卡片,卡片上的数是3的倍数的概率是______.
4.甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为_____.
你是怎样求出以上概率的?思考下列问题
若抛掷两枚硬币,一正,一反发生的概率又是多少呢
本节课学习目标:
1.理解为什么要列树状图或表格;
2.能熟练用画树状图或列表格的方法求不确定事件的概率.
以上视频讲述了,用画树状图的方法求概率
怎样用列表的方法,求概率呢?
第二枚硬币 第一枚硬币 正 反
正 (正,正) (正,反)
反 (反,正) (反,反)
共有4种情况,小明获胜的结果有一种,小明获胜的概率P(小明胜)=
小颖获胜的结果有一种,小颖获胜的概率P(小颖胜)=
小凡获胜的结果有一种,小凡获胜的概率P(小凡胜)=
例题学习1:
例1,在A、B两个盒子中都装入分别写有数字1、2的两张卡片,分别从每个盒子中任意取出一张卡片,两张卡片上的数字之和为3的概率是多少?
B盒 A盒 1 2
1 (1,1) (1,2)
2 (2,1) (2,2)
随堂练习:
例题学习2:
例2,小明,小颖,小凡做“石头、剪刀、布”的游戏,游戏规则如下:
由小明和小颖玩“石头、剪刀、布”的游戏如果两人的手势相同,那么小凡获胜;
如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的胜者。假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?
随堂练习:
3.小亮从语文、数学、英语3本课本中任意抽取一本,又从这3门课的作业中任意抽取一本,课本和作业恰好为同一门课的概率是多少?
4、小明和小军作掷骰子游戏,两人各掷一枚均匀的骰子。
(1)若两人掷得点数之和为奇数,则小军获胜,否则小明获胜,这个游戏对双方公平吗?为什么?
(2)若两人掷得点数之和为奇数,则小军获胜,否则小明获胜,这个游戏对双方公平吗?为什么?
课堂小结:
1、用画树状图或列表的方法求概率
2、画树状图与列表有什么优点?说说你的想法。
集中练习:
C
中考题欣赏1:
1、某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
(1)本次问卷调查共调查了________名观众;图②中最喜爱“体育节目”的扇形圆心角度数是________.
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为A),“体育节目”(记为B),“综艺节目”(记为C),“科普节目”(记为D)的观众各一名,电视台要从四人中随机抽取
两人参加联谊活动,请用列表或画树状图的方法,
求出恰好抽到最喜爱“B”和“C”两位观众的概率.
中考题欣赏2:
2.某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
根据图中信息解决下列问题:
(1)本次共调查 名学生,扇形统计图中B所对应的扇形的圆心角为 度;
(2)补全条形统计图;
(3)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
