2021-2022学年上海市金山区罗星中学八年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年上海市金山区罗星中学八年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 653.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 07:30:52 | ||
图片预览




文档简介
2021-2022学年上海市金山区罗星中学八年级第一学期期中数学试卷
一、选择题(本大题6题,每题3分,满分18分)
1.下列二次根式中,最简二次根式是( )
A. B.
C. D.
2.在下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
3.下列说法正确的是( )
A.方程4x2=x只有一个实数根
B.方程x2﹣25=0有两个相等的实数根
C.方程x2﹣x+3=0有两个不相等的实数根
D.方程2x2﹣2x+1=0没有实数根
4.关于x的一元二次方程ax2+bx+c=0(a≠0)中,它的一个根为﹣1,则( )
A.a+b+c=0 B.a+b﹣c=0 C.a﹣b+c=0 D.a﹣b﹣c=0
5.关于函数y=﹣x,以下说法错误的是( )
A.图象经过原点 B.图象经过第二、四象限
C.图象经过点 D.y的值随x的增大而增大
6.如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一根的一半,则称这样的方程为“半根方程”.以下关于半根方程的说法,正确的是( )
A.若方程(x﹣2)(mx+n)=0是半根方程,则4m2+5mn+n2=0
B.方程x2﹣x﹣2=0是半根方程
C.方程x2﹣4=0是半根方程
D.若点A(m,n)在函数y=2x的图象上,则关于x的方程mx2﹣n=0是半根方程
二、填空题(本大题共12题,每题2分,满分24分)
7.化简:= .
8.如果有意义,那么x的取值范围是 .
9.二次根式+4的一个有理化因式是 .
10.化简= .
11.一元二次方程x2﹣6x+9=0的实数根是 .
12.已知x=2﹣,那么(x﹣2)2﹣x的值为 .
13.以3,﹣2为两根,且二次项系数为1的一元二次方程的一般式是 .
14.在实数范围内因式分解:y2﹣2y﹣1= .
15.已知f(x)=,那么= .
16.如果函数y=(m+1)x+m2﹣1是正比例函数.则m的值是 .
17.不等式的解集是 .
18.若关于x的方程x2+kx+6=0的根是整数,且k<0,则k的值是 .
三、解答题(本大题共9题,19--22每题6分,23-25每题8分,26题10分,满分58分)
19.计算:.
20.化简:8x2(x>0).
21.解方程:2x2﹣4x﹣3=0.
22.解方程:(x﹣2)2+3(2﹣x)﹣10=0.
23.化简并求值:,其中x=.
24.已知关于x的方程x2﹣(2m﹣2)x+m2=0有两个实数根.
(1)求m的取值范围;
(2)当m取最大非零整数时,求方程的两个根.
25.去年某商店第一季度营业额为120万元,第二季度的营业额比第一季度增长了25%,第三、第四季度营业额的增长率相同,且第四季度的营业额为216万元.
求:(1)该店第二季度的营业额;
(2)该店第三、第四季度营业额的增长率.
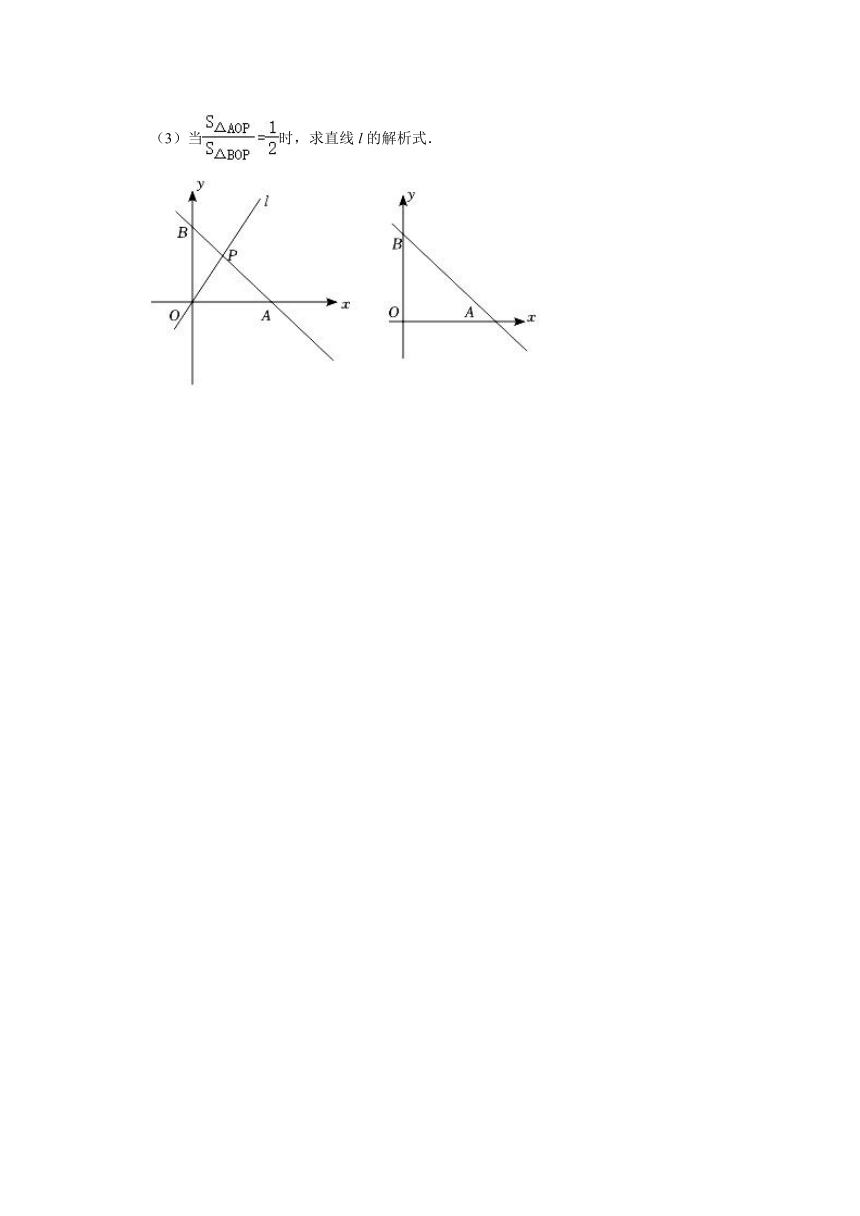
26.如图,在平面直角坐标系中,点A(6,0)、点B(0,6),过原点的直线l交直线AB于点P.
(1)求∠OAB的度数和△AOB的面积;
(2)当直线l的解析式为y=2x时,求点P的坐标;
(3)当时,求直线l的解析式.
参考答案
一、选择题(本大题6题,每题3分,满分18分)
1.下列二次根式中,最简二次根式是( )
A. B.
C. D.
【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解:A、可化为,不是最简二次根式;
B、是最简二次根式;
C、可化为|x|,不是最简二次根式;
D、可化为|x﹣y|,不是最简二次根式.
故选:B.
2.在下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
【分析】先将各选项化简,再找到被开方数为a的选项即可.
解:A、a与被开方数不同,故不是同类二次根式;
B、=|a|与被开方数不同,故不是同类二次根式;
C、=|a|与被开方数相同,故是同类二次根式;
D、=a2与被开方数不同,故不是同类二次根式.
故选:C.
3.下列说法正确的是( )
A.方程4x2=x只有一个实数根
B.方程x2﹣25=0有两个相等的实数根
C.方程x2﹣x+3=0有两个不相等的实数根
D.方程2x2﹣2x+1=0没有实数根
【分析】A.将原方程变形为一般式,由根的判别式Δ=1>0,可得出方程4x2=x有两个不相等的实数根,选项A不符合题意;
B.根据方程的系数结合根的判别式Δ=b2﹣4ac,可得出Δ=100>0,进而可得出方程x2﹣25=0有两个不相等的实数根,选项B不符合题意;
C.根据方程的系数结合根的判别式Δ=b2﹣4ac,可得出Δ=﹣11<0,进而可得出方程x2﹣x+3=0没有实数根,选项C不符合题意;
D.根据方程的系数结合根的判别式Δ=b2﹣4ac,可得出Δ=﹣4<0,进而可得出方程2x2﹣2x+1=0没有实数根,选项D符合题意.
解:A.原方程变形为一般式为4x2﹣x=0,
∴Δ=b2﹣4ac=(﹣1)2﹣4×4×0=1>0,
∴方程4x2=x有两个不相等的实数根,选项A不符合题意;
B.∵Δ=b2﹣4ac=02﹣4×1×(﹣25)=100>0,
∴方程x2﹣25=0有两个不相等的实数根,选项B不符合题意;
C.∵Δ=b2﹣4ac=(﹣1)2﹣4×1×3=﹣11<0,
∴方程x2﹣x+3=0没有实数根,选项C不符合题意;
D.∵Δ=b2﹣4ac=(﹣2)2﹣4×2×1=﹣4<0,
∴方程2x2﹣2x+1=0没有实数根,选项D符合题意.
故选:D.
4.关于x的一元二次方程ax2+bx+c=0(a≠0)中,它的一个根为﹣1,则( )
A.a+b+c=0 B.a+b﹣c=0 C.a﹣b+c=0 D.a﹣b﹣c=0
【分析】直接把x=﹣1代入方程得到a、b、c的关系,从而可对各选项进行判断.
解:把x=﹣1代入方程ax2+bx+c=0(a≠0)得a﹣b+c=0.
故选:C.
5.关于函数y=﹣x,以下说法错误的是( )
A.图象经过原点 B.图象经过第二、四象限
C.图象经过点 D.y的值随x的增大而增大
【分析】根据正比例函数的定义与性质判定即可.
解:A、由解析式可得它是正比例函数,故函数图象经过原点,说法正确,不合题意;
B、由k<0可得图象经过二、四象限,说法正确,不合题意;
C、当x=时,y=﹣2,图象经过点(,﹣),说法正确,不合题意;
D、由k<0可得y的值随x的增大而减小,说法错误,符合题意;
故选:D.
6.如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一根的一半,则称这样的方程为“半根方程”.以下关于半根方程的说法,正确的是( )
A.若方程(x﹣2)(mx+n)=0是半根方程,则4m2+5mn+n2=0
B.方程x2﹣x﹣2=0是半根方程
C.方程x2﹣4=0是半根方程
D.若点A(m,n)在函数y=2x的图象上,则关于x的方程mx2﹣n=0是半根方程
【分析】得方程的解后即可利用半根方程的定义进行判断.
解:A.∵方程(x﹣2)(mx+n)=0是半根方程,且x1=2,x2=﹣,
∴﹣=1或﹣=4,
∴m+n=0,4m+n=0,
∵4m2+5mn+n2=(4m+n)(m+n)=0,此结论正确.
B.方程x2﹣x﹣2=0的解为x1=﹣1、x2=2,此方程不是半根方程,此结论错误;
C.方程x2﹣4=0的解为x1=2、x2=﹣2,此方程不是半根方程,此结论错误;
D.∵点A(m,n)在函数y=2x的图象上,
∴n=2m,
解方程mx2﹣2m=0得:x1=,x2=﹣,
∴此方程不是半根方程,此结论错误;
故选:A.
二、填空题(本大题共12题,每题2分,满分24分)
7.化简:= 4 .
【分析】根据二次根式的乘法,可化简二次根式.
解:,
故答案为:4.
8.如果有意义,那么x的取值范围是 x>﹣2 .
【分析】利用二次根式有意义的条件和分母不为0得到x+2>0,然后解不等式即可.
解:根据题意得x+2>0,
解得x>﹣2.
故答案为x>﹣2.
9.二次根式+4的一个有理化因式是 ﹣4 .
【分析】由(+4) (﹣4)=a﹣16可得答案.
解:∵(+4) (﹣4)=a﹣16,
∴+4的一个有理化因式为﹣4,
故答案为:﹣4.
10.化简= ﹣2 .
【分析】根据二次根式的性质即可求出答案.
解:=
故答案为:
11.一元二次方程x2﹣6x+9=0的实数根是 x1=x2=3 .
【分析】先把左边直接配方,得(x﹣3)2=0,直接开平方即可.
解:配方,得(x﹣3)2=0,
直接开平方,得x﹣3=0,
∴方程的解为x1=x2=3,
故答案为x1=x2=3.
12.已知x=2﹣,那么(x﹣2)2﹣x的值为 .
【分析】先把x的值代入(x﹣2)2﹣x中,然后利用二次根式的性质计算.
解:∵x=2﹣,
∴(x﹣2)2﹣x=(2﹣﹣2)2﹣(2﹣)
=2﹣2+
=.
故答案为.
13.以3,﹣2为两根,且二次项系数为1的一元二次方程的一般式是 x2﹣x﹣6=0(答案不唯一) .
【分析】设满足题意的一元二次方程为ax2+bx+c=0,利用根与系数的关系可得出﹣=1,=﹣6,代入a=1可求出b,c的值,进而可得出满足题意的一元二次方程可以为x2﹣x﹣6=0.
解:设满足题意的一元二次方程为ax2+bx+c=0.
∵方程的两个根分别为3和﹣2,
∴﹣=3+(﹣2)=1,=3×(﹣2)=﹣6,
∴当a=1时,b=﹣1,c=﹣6,
∴满足题意的一元二次方程可以为x2﹣x﹣6=0.
故答案为:x2﹣x﹣6=0(答案不唯一).
14.在实数范围内因式分解:y2﹣2y﹣1= (y﹣1+)(y﹣1﹣) .
【分析】变形整式为y2﹣2y+1﹣2,前三项利用完全平方公式,再利用平方差公式因式分解.
解:y2﹣2y﹣1
=y2﹣2y+1﹣2
=(y﹣1)2﹣2
=(y﹣1+)(y﹣1﹣).
故答案为:(y﹣1+)(y﹣1﹣).
15.已知f(x)=,那么= .
【分析】把x=代入函数关系式进行计算即可.
解:f()==,
故答案为:.
16.如果函数y=(m+1)x+m2﹣1是正比例函数.则m的值是 1 .
【分析】由正比例函数的定义:可得m2﹣1=0,且m+1≠0,然后解关于m的一元二次方程即可.
解:由正比例函数的定义可得:m2﹣1=0,且m+1≠0,
解得,m=1;
故答案为:1.
17.不等式的解集是 x<﹣﹣ .
【分析】利用解不等式的方法与步骤求得解集,进一步化简即可.
解:,
x﹣x<﹣1,
x<﹣,
x<﹣﹣.
故答案为:x<﹣﹣.
18.若关于x的方程x2+kx+6=0的根是整数,且k<0,则k的值是 ﹣5或﹣7 .
【分析】由根与系数的关系得x1 x2=6,由关于x的方程x2+kx+6=0的根是整数,且k<0,得到x1=﹣2,x2=﹣3;x1=﹣1,x2=﹣6,进一步求得k的值.
解:设于x的方程x2+kx+6=0的根为x1、x2,则x1 x2=6,
∵关于x的方程x2+kx+6=0的根是整数,且k<0,
∴x1=﹣2,x2=﹣3;x1=﹣1,x2=﹣6,
∴相应k的值为﹣5或﹣7.
故答案为:﹣5或﹣7.
三、解答题(本大题共9题,19--22每题6分,23-25每题8分,26题10分,满分58分)
19.计算:.
【分析】直接利用二次根式的性质分别化简,进而合并得出答案.
解:原式=3+﹣(+)
=﹣2
=.
20.化简:8x2(x>0).
【分析】根据二次根式有意义的条件和x的取值范围,确定y的取值范围,再根据二次根式的性质和乘除法的法则进行计算即可.
解:∵x>0,有意义,
∴y>0,
∴原式=8x2÷×
=×
=2y2.
21.解方程:2x2﹣4x﹣3=0.
【分析】公式法求解可得.
解:∵a=2,b=﹣4,c=﹣3,
∴△=16﹣4×2×(﹣3)=40>0,
则x==.
22.解方程:(x﹣2)2+3(2﹣x)﹣10=0.
【分析】将x﹣2看作整体,利用因式分解法求解可得.
解:(x﹣2)2+3(2﹣x)﹣10=0,
(x﹣2)2﹣3(x﹣2)﹣10=0,
∴(x﹣2﹣5)(x﹣2+2)=0,即x(x﹣7)=0,
∴x=0或x﹣7=0,
∴x1=0,x2=7.
23.化简并求值:,其中x=.
【分析】利用因式分解的方法把原式变形为 ,利用约分得到原式=x﹣y,再把x、y的值化简后代入计算即可.
解:原式=
=(﹣) (+)
=x﹣y,
∵x==﹣1,y==,
∴原式=﹣1﹣
=﹣1.
24.已知关于x的方程x2﹣(2m﹣2)x+m2=0有两个实数根.
(1)求m的取值范围;
(2)当m取最大非零整数时,求方程的两个根.
【分析】(1)根据方程的系数结合根的判别式Δ≥0,即可得出关于m的一元一次不等式,解之即可得出m的取值范围;
(2)由(1)的结论可得出m可取的最大非零整数为﹣1,将其代入原方程中,再利用公式法解一元二次方程,即可求出此时方程的两个根.
解:(1)∵关于x的方程x2﹣(2m﹣2)x+m2=0有两个实数根,
∴Δ=b2﹣4ac=[﹣(2m﹣2)]2﹣4×1×m2=4﹣8m≥0,
解得:m≤,
∴m的取值范围为m≤.
(2)∵m≤,
∴当m取最大非零整数时,m=﹣1.
当m=﹣1时,原方程为x2+4x+1=0,
解得:x1==﹣2﹣,x2==﹣2+.
∴当m取最大非零整数时,方程的两个根分别为x1=﹣2﹣,x2=﹣2+.
25.去年某商店第一季度营业额为120万元,第二季度的营业额比第一季度增长了25%,第三、第四季度营业额的增长率相同,且第四季度的营业额为216万元.
求:(1)该店第二季度的营业额;
(2)该店第三、第四季度营业额的增长率.
【分析】(1)根据某商店第一季度营业额为120万元,第二季度的营业额比第一季度增长了25%,可以计算出第二季度的营业额;
(2)根据(1)中的结果和第三、第四季度营业额的增长率相同,且第四季度的营业额为216万元,可以得到方程150(1+x)2=216,然后求解即可.
解:(1)由题意可得,
第二季度的营业额为:120×(1+25%)=120×=150(万元),
答:该店第二季度的营业额为150万元;
(2)设该店第三、第四季度营业额的增长率为x,
150(1+x)2=216,
解得x1=0.2,x2=﹣2.2(舍去),
答:该店第三、第四季度营业额的增长率是20%.
26.如图,在平面直角坐标系中,点A(6,0)、点B(0,6),过原点的直线l交直线AB于点P.
(1)求∠OAB的度数和△AOB的面积;
(2)当直线l的解析式为y=2x时,求点P的坐标;
(3)当时,求直线l的解析式.
【分析】(1)可得出OA=OB,∠AOB=90°,从而求得结果;
(2)求出l的解析式,与y=2x联立方程组,解得结果;
(3)分为点P在BA上和BA的延长线上,当点P在AB上时,作PC⊥OA于C,作PD⊥OB于D,可推出PD=2PC,代入y=﹣x+6求得;当点P在BA的延长线上时,作OE⊥AB于E,作PF⊥OA于F,求得AP=BP=6,进而求得结果.
解:(1)∵A(6,0),B(0,6),
∴OA=OB=6,
∵∠AOB=90°,
∴∠OAB=∠OBA
=
=
=45°,
S△AOB===18;
(2)设直线AB的解析式是:y=kx+b,
∴,
∴,
∴y=﹣x+6,
∴,
∴,
∴P(2,4);
(3)如图1,
设点P(a,b),
当点P在AB上时,
作PC⊥OA于C,作PD⊥OB于D,
∵,
∴=,
∵OA=OB,
∴=,
∴PD=2PC,
∴a=2b,
又∵b=﹣a+6,
∴a=4,b=2,
∴P(4,2),
∴直线l的解析式是:y=x,
如图2,
当点P在BA的延长线上时,
作OE⊥AB于E,作PF⊥OA于F,
∴∠AFP=∠AOB=90°,
∵,
∴=,
∴AP=BP,
∴AP=AB,
∵∠OAB=∠PAF,
∴△APF≌△ABO(AAS),
∴AF=OA=6,PF=OB=6,
∴OF=12,
∴P(12,﹣6),
∴直线l的解析式是:y=﹣;
综上所述:直线l的解析式是:y=或y=﹣x.
一、选择题(本大题6题,每题3分,满分18分)
1.下列二次根式中,最简二次根式是( )
A. B.
C. D.
2.在下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
3.下列说法正确的是( )
A.方程4x2=x只有一个实数根
B.方程x2﹣25=0有两个相等的实数根
C.方程x2﹣x+3=0有两个不相等的实数根
D.方程2x2﹣2x+1=0没有实数根
4.关于x的一元二次方程ax2+bx+c=0(a≠0)中,它的一个根为﹣1,则( )
A.a+b+c=0 B.a+b﹣c=0 C.a﹣b+c=0 D.a﹣b﹣c=0
5.关于函数y=﹣x,以下说法错误的是( )
A.图象经过原点 B.图象经过第二、四象限
C.图象经过点 D.y的值随x的增大而增大
6.如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一根的一半,则称这样的方程为“半根方程”.以下关于半根方程的说法,正确的是( )
A.若方程(x﹣2)(mx+n)=0是半根方程,则4m2+5mn+n2=0
B.方程x2﹣x﹣2=0是半根方程
C.方程x2﹣4=0是半根方程
D.若点A(m,n)在函数y=2x的图象上,则关于x的方程mx2﹣n=0是半根方程
二、填空题(本大题共12题,每题2分,满分24分)
7.化简:= .
8.如果有意义,那么x的取值范围是 .
9.二次根式+4的一个有理化因式是 .
10.化简= .
11.一元二次方程x2﹣6x+9=0的实数根是 .
12.已知x=2﹣,那么(x﹣2)2﹣x的值为 .
13.以3,﹣2为两根,且二次项系数为1的一元二次方程的一般式是 .
14.在实数范围内因式分解:y2﹣2y﹣1= .
15.已知f(x)=,那么= .
16.如果函数y=(m+1)x+m2﹣1是正比例函数.则m的值是 .
17.不等式的解集是 .
18.若关于x的方程x2+kx+6=0的根是整数,且k<0,则k的值是 .
三、解答题(本大题共9题,19--22每题6分,23-25每题8分,26题10分,满分58分)
19.计算:.
20.化简:8x2(x>0).
21.解方程:2x2﹣4x﹣3=0.
22.解方程:(x﹣2)2+3(2﹣x)﹣10=0.
23.化简并求值:,其中x=.
24.已知关于x的方程x2﹣(2m﹣2)x+m2=0有两个实数根.
(1)求m的取值范围;
(2)当m取最大非零整数时,求方程的两个根.
25.去年某商店第一季度营业额为120万元,第二季度的营业额比第一季度增长了25%,第三、第四季度营业额的增长率相同,且第四季度的营业额为216万元.
求:(1)该店第二季度的营业额;
(2)该店第三、第四季度营业额的增长率.
26.如图,在平面直角坐标系中,点A(6,0)、点B(0,6),过原点的直线l交直线AB于点P.
(1)求∠OAB的度数和△AOB的面积;
(2)当直线l的解析式为y=2x时,求点P的坐标;
(3)当时,求直线l的解析式.
参考答案
一、选择题(本大题6题,每题3分,满分18分)
1.下列二次根式中,最简二次根式是( )
A. B.
C. D.
【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解:A、可化为,不是最简二次根式;
B、是最简二次根式;
C、可化为|x|,不是最简二次根式;
D、可化为|x﹣y|,不是最简二次根式.
故选:B.
2.在下列二次根式中,与是同类二次根式的是( )
A. B. C. D.
【分析】先将各选项化简,再找到被开方数为a的选项即可.
解:A、a与被开方数不同,故不是同类二次根式;
B、=|a|与被开方数不同,故不是同类二次根式;
C、=|a|与被开方数相同,故是同类二次根式;
D、=a2与被开方数不同,故不是同类二次根式.
故选:C.
3.下列说法正确的是( )
A.方程4x2=x只有一个实数根
B.方程x2﹣25=0有两个相等的实数根
C.方程x2﹣x+3=0有两个不相等的实数根
D.方程2x2﹣2x+1=0没有实数根
【分析】A.将原方程变形为一般式,由根的判别式Δ=1>0,可得出方程4x2=x有两个不相等的实数根,选项A不符合题意;
B.根据方程的系数结合根的判别式Δ=b2﹣4ac,可得出Δ=100>0,进而可得出方程x2﹣25=0有两个不相等的实数根,选项B不符合题意;
C.根据方程的系数结合根的判别式Δ=b2﹣4ac,可得出Δ=﹣11<0,进而可得出方程x2﹣x+3=0没有实数根,选项C不符合题意;
D.根据方程的系数结合根的判别式Δ=b2﹣4ac,可得出Δ=﹣4<0,进而可得出方程2x2﹣2x+1=0没有实数根,选项D符合题意.
解:A.原方程变形为一般式为4x2﹣x=0,
∴Δ=b2﹣4ac=(﹣1)2﹣4×4×0=1>0,
∴方程4x2=x有两个不相等的实数根,选项A不符合题意;
B.∵Δ=b2﹣4ac=02﹣4×1×(﹣25)=100>0,
∴方程x2﹣25=0有两个不相等的实数根,选项B不符合题意;
C.∵Δ=b2﹣4ac=(﹣1)2﹣4×1×3=﹣11<0,
∴方程x2﹣x+3=0没有实数根,选项C不符合题意;
D.∵Δ=b2﹣4ac=(﹣2)2﹣4×2×1=﹣4<0,
∴方程2x2﹣2x+1=0没有实数根,选项D符合题意.
故选:D.
4.关于x的一元二次方程ax2+bx+c=0(a≠0)中,它的一个根为﹣1,则( )
A.a+b+c=0 B.a+b﹣c=0 C.a﹣b+c=0 D.a﹣b﹣c=0
【分析】直接把x=﹣1代入方程得到a、b、c的关系,从而可对各选项进行判断.
解:把x=﹣1代入方程ax2+bx+c=0(a≠0)得a﹣b+c=0.
故选:C.
5.关于函数y=﹣x,以下说法错误的是( )
A.图象经过原点 B.图象经过第二、四象限
C.图象经过点 D.y的值随x的增大而增大
【分析】根据正比例函数的定义与性质判定即可.
解:A、由解析式可得它是正比例函数,故函数图象经过原点,说法正确,不合题意;
B、由k<0可得图象经过二、四象限,说法正确,不合题意;
C、当x=时,y=﹣2,图象经过点(,﹣),说法正确,不合题意;
D、由k<0可得y的值随x的增大而减小,说法错误,符合题意;
故选:D.
6.如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一根的一半,则称这样的方程为“半根方程”.以下关于半根方程的说法,正确的是( )
A.若方程(x﹣2)(mx+n)=0是半根方程,则4m2+5mn+n2=0
B.方程x2﹣x﹣2=0是半根方程
C.方程x2﹣4=0是半根方程
D.若点A(m,n)在函数y=2x的图象上,则关于x的方程mx2﹣n=0是半根方程
【分析】得方程的解后即可利用半根方程的定义进行判断.
解:A.∵方程(x﹣2)(mx+n)=0是半根方程,且x1=2,x2=﹣,
∴﹣=1或﹣=4,
∴m+n=0,4m+n=0,
∵4m2+5mn+n2=(4m+n)(m+n)=0,此结论正确.
B.方程x2﹣x﹣2=0的解为x1=﹣1、x2=2,此方程不是半根方程,此结论错误;
C.方程x2﹣4=0的解为x1=2、x2=﹣2,此方程不是半根方程,此结论错误;
D.∵点A(m,n)在函数y=2x的图象上,
∴n=2m,
解方程mx2﹣2m=0得:x1=,x2=﹣,
∴此方程不是半根方程,此结论错误;
故选:A.
二、填空题(本大题共12题,每题2分,满分24分)
7.化简:= 4 .
【分析】根据二次根式的乘法,可化简二次根式.
解:,
故答案为:4.
8.如果有意义,那么x的取值范围是 x>﹣2 .
【分析】利用二次根式有意义的条件和分母不为0得到x+2>0,然后解不等式即可.
解:根据题意得x+2>0,
解得x>﹣2.
故答案为x>﹣2.
9.二次根式+4的一个有理化因式是 ﹣4 .
【分析】由(+4) (﹣4)=a﹣16可得答案.
解:∵(+4) (﹣4)=a﹣16,
∴+4的一个有理化因式为﹣4,
故答案为:﹣4.
10.化简= ﹣2 .
【分析】根据二次根式的性质即可求出答案.
解:=
故答案为:
11.一元二次方程x2﹣6x+9=0的实数根是 x1=x2=3 .
【分析】先把左边直接配方,得(x﹣3)2=0,直接开平方即可.
解:配方,得(x﹣3)2=0,
直接开平方,得x﹣3=0,
∴方程的解为x1=x2=3,
故答案为x1=x2=3.
12.已知x=2﹣,那么(x﹣2)2﹣x的值为 .
【分析】先把x的值代入(x﹣2)2﹣x中,然后利用二次根式的性质计算.
解:∵x=2﹣,
∴(x﹣2)2﹣x=(2﹣﹣2)2﹣(2﹣)
=2﹣2+
=.
故答案为.
13.以3,﹣2为两根,且二次项系数为1的一元二次方程的一般式是 x2﹣x﹣6=0(答案不唯一) .
【分析】设满足题意的一元二次方程为ax2+bx+c=0,利用根与系数的关系可得出﹣=1,=﹣6,代入a=1可求出b,c的值,进而可得出满足题意的一元二次方程可以为x2﹣x﹣6=0.
解:设满足题意的一元二次方程为ax2+bx+c=0.
∵方程的两个根分别为3和﹣2,
∴﹣=3+(﹣2)=1,=3×(﹣2)=﹣6,
∴当a=1时,b=﹣1,c=﹣6,
∴满足题意的一元二次方程可以为x2﹣x﹣6=0.
故答案为:x2﹣x﹣6=0(答案不唯一).
14.在实数范围内因式分解:y2﹣2y﹣1= (y﹣1+)(y﹣1﹣) .
【分析】变形整式为y2﹣2y+1﹣2,前三项利用完全平方公式,再利用平方差公式因式分解.
解:y2﹣2y﹣1
=y2﹣2y+1﹣2
=(y﹣1)2﹣2
=(y﹣1+)(y﹣1﹣).
故答案为:(y﹣1+)(y﹣1﹣).
15.已知f(x)=,那么= .
【分析】把x=代入函数关系式进行计算即可.
解:f()==,
故答案为:.
16.如果函数y=(m+1)x+m2﹣1是正比例函数.则m的值是 1 .
【分析】由正比例函数的定义:可得m2﹣1=0,且m+1≠0,然后解关于m的一元二次方程即可.
解:由正比例函数的定义可得:m2﹣1=0,且m+1≠0,
解得,m=1;
故答案为:1.
17.不等式的解集是 x<﹣﹣ .
【分析】利用解不等式的方法与步骤求得解集,进一步化简即可.
解:,
x﹣x<﹣1,
x<﹣,
x<﹣﹣.
故答案为:x<﹣﹣.
18.若关于x的方程x2+kx+6=0的根是整数,且k<0,则k的值是 ﹣5或﹣7 .
【分析】由根与系数的关系得x1 x2=6,由关于x的方程x2+kx+6=0的根是整数,且k<0,得到x1=﹣2,x2=﹣3;x1=﹣1,x2=﹣6,进一步求得k的值.
解:设于x的方程x2+kx+6=0的根为x1、x2,则x1 x2=6,
∵关于x的方程x2+kx+6=0的根是整数,且k<0,
∴x1=﹣2,x2=﹣3;x1=﹣1,x2=﹣6,
∴相应k的值为﹣5或﹣7.
故答案为:﹣5或﹣7.
三、解答题(本大题共9题,19--22每题6分,23-25每题8分,26题10分,满分58分)
19.计算:.
【分析】直接利用二次根式的性质分别化简,进而合并得出答案.
解:原式=3+﹣(+)
=﹣2
=.
20.化简:8x2(x>0).
【分析】根据二次根式有意义的条件和x的取值范围,确定y的取值范围,再根据二次根式的性质和乘除法的法则进行计算即可.
解:∵x>0,有意义,
∴y>0,
∴原式=8x2÷×
=×
=2y2.
21.解方程:2x2﹣4x﹣3=0.
【分析】公式法求解可得.
解:∵a=2,b=﹣4,c=﹣3,
∴△=16﹣4×2×(﹣3)=40>0,
则x==.
22.解方程:(x﹣2)2+3(2﹣x)﹣10=0.
【分析】将x﹣2看作整体,利用因式分解法求解可得.
解:(x﹣2)2+3(2﹣x)﹣10=0,
(x﹣2)2﹣3(x﹣2)﹣10=0,
∴(x﹣2﹣5)(x﹣2+2)=0,即x(x﹣7)=0,
∴x=0或x﹣7=0,
∴x1=0,x2=7.
23.化简并求值:,其中x=.
【分析】利用因式分解的方法把原式变形为 ,利用约分得到原式=x﹣y,再把x、y的值化简后代入计算即可.
解:原式=
=(﹣) (+)
=x﹣y,
∵x==﹣1,y==,
∴原式=﹣1﹣
=﹣1.
24.已知关于x的方程x2﹣(2m﹣2)x+m2=0有两个实数根.
(1)求m的取值范围;
(2)当m取最大非零整数时,求方程的两个根.
【分析】(1)根据方程的系数结合根的判别式Δ≥0,即可得出关于m的一元一次不等式,解之即可得出m的取值范围;
(2)由(1)的结论可得出m可取的最大非零整数为﹣1,将其代入原方程中,再利用公式法解一元二次方程,即可求出此时方程的两个根.
解:(1)∵关于x的方程x2﹣(2m﹣2)x+m2=0有两个实数根,
∴Δ=b2﹣4ac=[﹣(2m﹣2)]2﹣4×1×m2=4﹣8m≥0,
解得:m≤,
∴m的取值范围为m≤.
(2)∵m≤,
∴当m取最大非零整数时,m=﹣1.
当m=﹣1时,原方程为x2+4x+1=0,
解得:x1==﹣2﹣,x2==﹣2+.
∴当m取最大非零整数时,方程的两个根分别为x1=﹣2﹣,x2=﹣2+.
25.去年某商店第一季度营业额为120万元,第二季度的营业额比第一季度增长了25%,第三、第四季度营业额的增长率相同,且第四季度的营业额为216万元.
求:(1)该店第二季度的营业额;
(2)该店第三、第四季度营业额的增长率.
【分析】(1)根据某商店第一季度营业额为120万元,第二季度的营业额比第一季度增长了25%,可以计算出第二季度的营业额;
(2)根据(1)中的结果和第三、第四季度营业额的增长率相同,且第四季度的营业额为216万元,可以得到方程150(1+x)2=216,然后求解即可.
解:(1)由题意可得,
第二季度的营业额为:120×(1+25%)=120×=150(万元),
答:该店第二季度的营业额为150万元;
(2)设该店第三、第四季度营业额的增长率为x,
150(1+x)2=216,
解得x1=0.2,x2=﹣2.2(舍去),
答:该店第三、第四季度营业额的增长率是20%.
26.如图,在平面直角坐标系中,点A(6,0)、点B(0,6),过原点的直线l交直线AB于点P.
(1)求∠OAB的度数和△AOB的面积;
(2)当直线l的解析式为y=2x时,求点P的坐标;
(3)当时,求直线l的解析式.
【分析】(1)可得出OA=OB,∠AOB=90°,从而求得结果;
(2)求出l的解析式,与y=2x联立方程组,解得结果;
(3)分为点P在BA上和BA的延长线上,当点P在AB上时,作PC⊥OA于C,作PD⊥OB于D,可推出PD=2PC,代入y=﹣x+6求得;当点P在BA的延长线上时,作OE⊥AB于E,作PF⊥OA于F,求得AP=BP=6,进而求得结果.
解:(1)∵A(6,0),B(0,6),
∴OA=OB=6,
∵∠AOB=90°,
∴∠OAB=∠OBA
=
=
=45°,
S△AOB===18;
(2)设直线AB的解析式是:y=kx+b,
∴,
∴,
∴y=﹣x+6,
∴,
∴,
∴P(2,4);
(3)如图1,
设点P(a,b),
当点P在AB上时,
作PC⊥OA于C,作PD⊥OB于D,
∵,
∴=,
∵OA=OB,
∴=,
∴PD=2PC,
∴a=2b,
又∵b=﹣a+6,
∴a=4,b=2,
∴P(4,2),
∴直线l的解析式是:y=x,
如图2,
当点P在BA的延长线上时,
作OE⊥AB于E,作PF⊥OA于F,
∴∠AFP=∠AOB=90°,
∵,
∴=,
∴AP=BP,
∴AP=AB,
∵∠OAB=∠PAF,
∴△APF≌△ABO(AAS),
∴AF=OA=6,PF=OB=6,
∴OF=12,
∴P(12,﹣6),
∴直线l的解析式是:y=﹣;
综上所述:直线l的解析式是:y=或y=﹣x.
同课章节目录
