人教版八年级上册13.1.2线段垂直平分线的性质教案
文档属性
| 名称 | 人教版八年级上册13.1.2线段垂直平分线的性质教案 |  | |
| 格式 | doc | ||
| 文件大小 | 111.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 11:01:51 | ||
图片预览

文档简介
《线段垂直平分线的性质》教案
目标和目标解析
基于以上的教学内容和本节课在初中几何中的重要地位作用,以及新课程标准中“培养学生自主学习和探索能力”的要求,我设定了以下教学目标:
(1)、知识与技能目标:
会用尺规作图画已知线段的垂直平分线并会证明;
理解并掌握线段的垂直平分线的性质及判定定理并能利用其进行简单的推理、计算,解决实际问题。
(2)、过程与方法目标:
经历线段的垂直平分线的画法、证明、性质的探究过程,提高学生的动手能力、观察能力及实验推理能力。
(3)情感、态度与价值观目标
通过主动探究,合作交流,进一步发展学生推理证明的意识和能力,感受探索的乐趣;
培养学生独立思考,积极思考的好习惯,同时强化合作交流的意识和能力。
教学重点 :探索线段垂直平分线的性质及应用,线段垂直平分线的画法及证明。
教学难点:线段的垂直平分线的作法的证明;线段的垂直平分线的性质的灵活应用。
教学过程设计
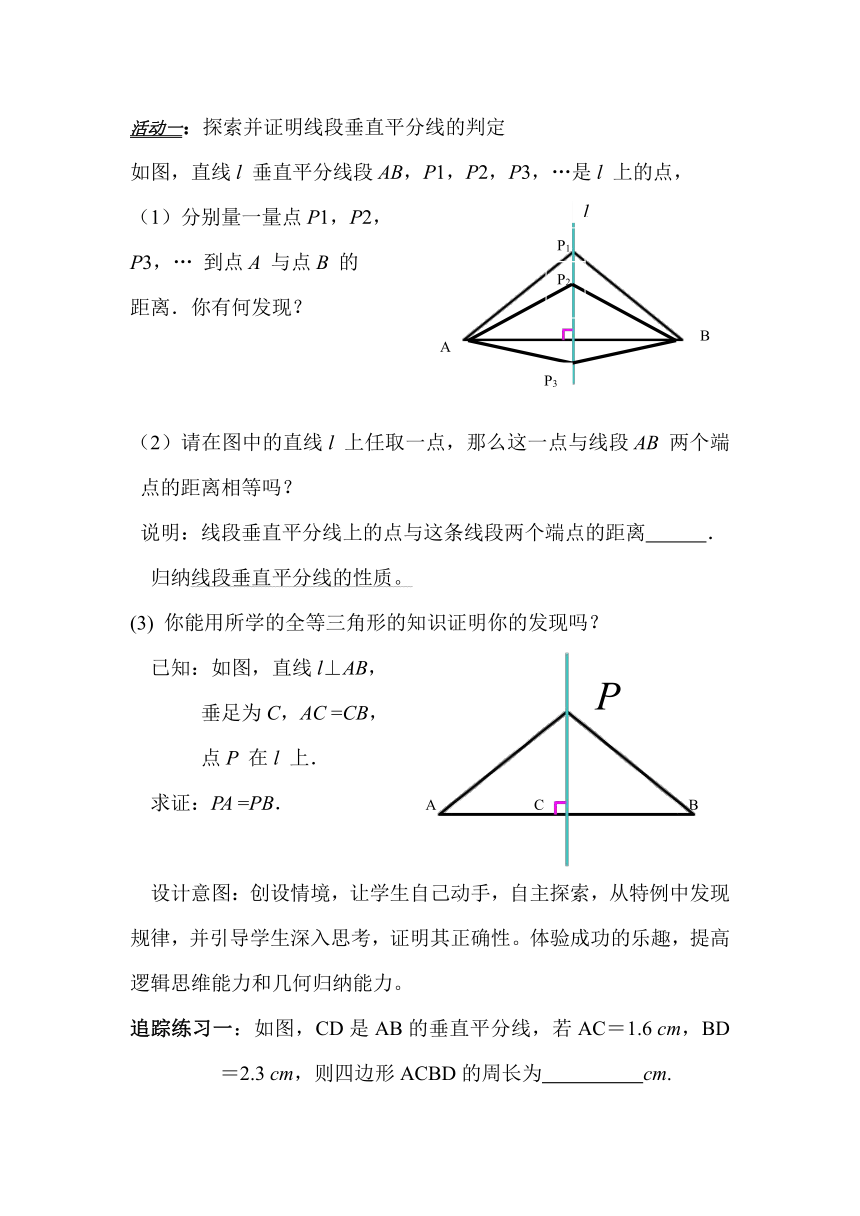
活动一:探索并证明线段垂直平分线的判定
如图,直线l 垂直平分线段AB,P1,P2,P3,…是l 上的点,
(1)分别量一量点P1,P2,
P3,… 到点A 与点B 的
距离.你有何发现?
(2)请在图中的直线l 上任取一点,那么这一点与线段AB 两个端点的距离相等吗?
说明:线段垂直平分线上的点与这条线段两个端点的距离 .
归纳线段垂直平分线的性质。
(3) 你能用所学的全等三角形的知识证明你的发现吗?
已知:如图,直线l⊥AB,
垂足为C,AC =CB,
点P 在l 上.
求证:PA =PB. A C B
设计意图:创设情境,让学生自己动手,自主探索,从特例中发现规律,并引导学生深入思考,证明其正确性。体验成功的乐趣,提高逻辑思维能力和几何归纳能力。
追踪练习一:如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长为 cm.
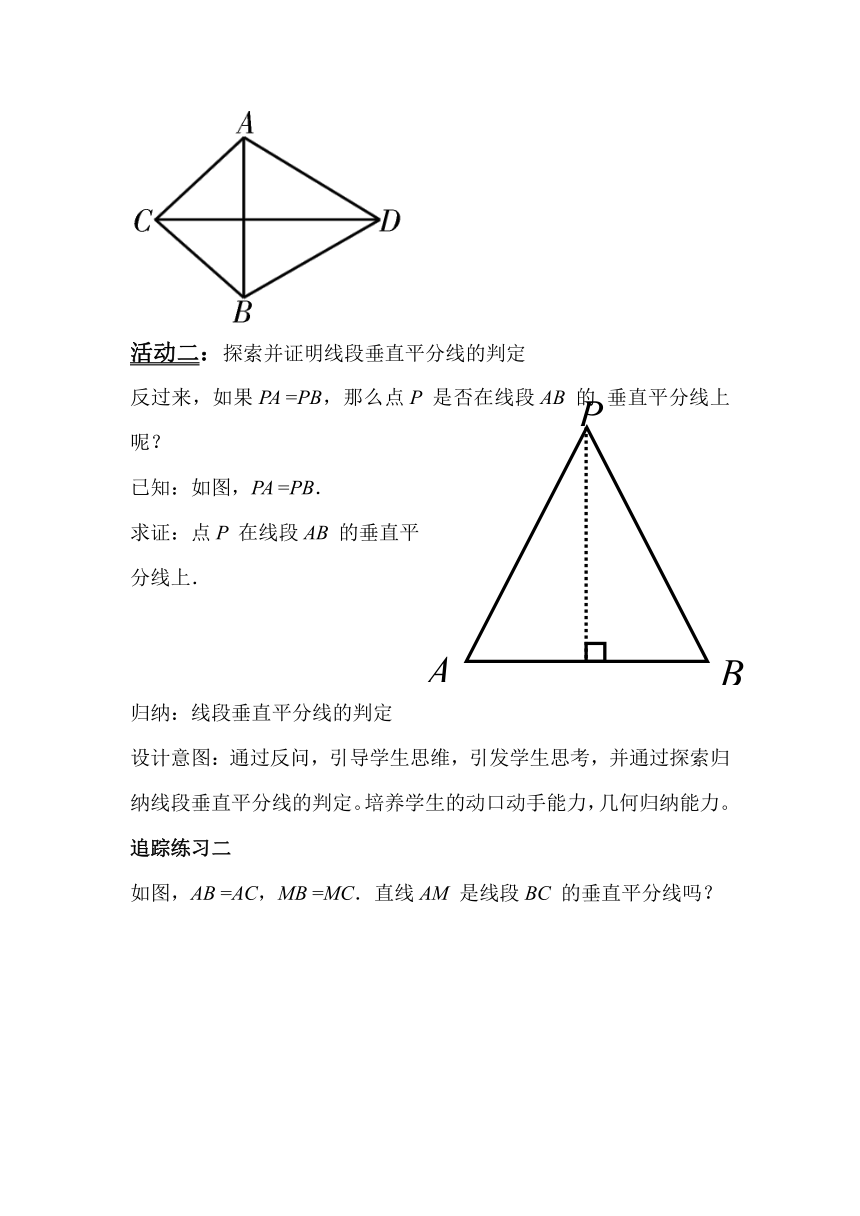
活动二:探索并证明线段垂直平分线的判定
反过来,如果PA =PB,那么点P 是否在线段AB 的 垂直平分线上呢?
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.
归纳:线段垂直平分线的判定
设计意图:通过反问,引导学生思维,引发学生思考,并通过探索归纳线段垂直平分线的判定。培养学生的动口动手能力,几何归纳能力。
追踪练习二
如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
活动三:尺规作图
如何用尺规作图的方法经过直线外一点作已知直线的垂线?
已知: 直线AB和直线AB外一点C
求作:直线AB的垂线,使其经过点C
思考:为什么直线CF 就是所求作的垂线?
设计意图:引导学生在作图方法的帮助下,自己动手操作,完成尺规作图,从而明确作图方法。并能从作图方法中找到条件加以验证。提高学生的语言表达能力及分析判断演绎推理的能力。这是本节课的难点之一。
活动四:快乐之旅(考考你)
“非常6+1”游戏规则:
7个金蛋你可以任选一个,如果出现“恭喜你”的字样,你们小组将直接过关;否则将有考验你们小组的数学问题。试试吧!
相关习题
1、如图,已知:在△ABC中,AB=AC,O 是△ABC内一点,且OB=OC,
求证:AO⊥BC.
2、如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段 的垂直平分线上.
3、如图,在△ABC中,AB=5 cm,AC=3 cm,BC的垂直平分线分别交AB,BC于点D,E,则△ACD的周长为 cm.
设计意图:通过游戏环节,一方面可以调动学生学习的积极性,在他们已经疲劳之时,重新吸引其注意力:另一方面,通过练习应用新知,加深学生对知识的理解和掌握,提高学生应用新知的能力。
活动五:课堂小结
11.3 角的平分线 12.1 线段的垂直平分
性质 在角的平分线上的点到这个角的 。 性质 线段垂直平分线上的点和这条线段 。
判定 的点,在这个角的平分线上。 判定 点,在这条线段的垂直平分线上。
角的平分线是 的所有点的集合。 线段的垂直平分线是 的所有点的集合。
一条 线 一条 线
设计意图:通过本环节,将本节课所学知识做一总结,同时与角平分线的知识进行对比,在对比中提高学生对新知的理解。并将所学知识做一线街,使学生融会贯通,避免在应用过程中的混淆。渗透对比,类比思想。
活动六: 作业布置
习题13.1 6题 、9题 、
问题解决: 某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
设计意图:一方面巩固基础知识,另一方面,把学生的眼光引向生活,使生活问题数学化,提高学生应用所学知识解决实际问题的能力,进一步感受数学来源于生活有服务于生活。
l
P1
P2
B
P3
A
P
P
A
B
A
B
C
D
M
O
D
E
A
B
P
C
目标和目标解析
基于以上的教学内容和本节课在初中几何中的重要地位作用,以及新课程标准中“培养学生自主学习和探索能力”的要求,我设定了以下教学目标:
(1)、知识与技能目标:
会用尺规作图画已知线段的垂直平分线并会证明;
理解并掌握线段的垂直平分线的性质及判定定理并能利用其进行简单的推理、计算,解决实际问题。
(2)、过程与方法目标:
经历线段的垂直平分线的画法、证明、性质的探究过程,提高学生的动手能力、观察能力及实验推理能力。
(3)情感、态度与价值观目标
通过主动探究,合作交流,进一步发展学生推理证明的意识和能力,感受探索的乐趣;
培养学生独立思考,积极思考的好习惯,同时强化合作交流的意识和能力。
教学重点 :探索线段垂直平分线的性质及应用,线段垂直平分线的画法及证明。
教学难点:线段的垂直平分线的作法的证明;线段的垂直平分线的性质的灵活应用。
教学过程设计
活动一:探索并证明线段垂直平分线的判定
如图,直线l 垂直平分线段AB,P1,P2,P3,…是l 上的点,
(1)分别量一量点P1,P2,
P3,… 到点A 与点B 的
距离.你有何发现?
(2)请在图中的直线l 上任取一点,那么这一点与线段AB 两个端点的距离相等吗?
说明:线段垂直平分线上的点与这条线段两个端点的距离 .
归纳线段垂直平分线的性质。
(3) 你能用所学的全等三角形的知识证明你的发现吗?
已知:如图,直线l⊥AB,
垂足为C,AC =CB,
点P 在l 上.
求证:PA =PB. A C B
设计意图:创设情境,让学生自己动手,自主探索,从特例中发现规律,并引导学生深入思考,证明其正确性。体验成功的乐趣,提高逻辑思维能力和几何归纳能力。
追踪练习一:如图,CD是AB的垂直平分线,若AC=1.6 cm,BD=2.3 cm,则四边形ACBD的周长为 cm.
活动二:探索并证明线段垂直平分线的判定
反过来,如果PA =PB,那么点P 是否在线段AB 的 垂直平分线上呢?
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.
归纳:线段垂直平分线的判定
设计意图:通过反问,引导学生思维,引发学生思考,并通过探索归纳线段垂直平分线的判定。培养学生的动口动手能力,几何归纳能力。
追踪练习二
如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
活动三:尺规作图
如何用尺规作图的方法经过直线外一点作已知直线的垂线?
已知: 直线AB和直线AB外一点C
求作:直线AB的垂线,使其经过点C
思考:为什么直线CF 就是所求作的垂线?
设计意图:引导学生在作图方法的帮助下,自己动手操作,完成尺规作图,从而明确作图方法。并能从作图方法中找到条件加以验证。提高学生的语言表达能力及分析判断演绎推理的能力。这是本节课的难点之一。
活动四:快乐之旅(考考你)
“非常6+1”游戏规则:
7个金蛋你可以任选一个,如果出现“恭喜你”的字样,你们小组将直接过关;否则将有考验你们小组的数学问题。试试吧!
相关习题
1、如图,已知:在△ABC中,AB=AC,O 是△ABC内一点,且OB=OC,
求证:AO⊥BC.
2、如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段 的垂直平分线上.
3、如图,在△ABC中,AB=5 cm,AC=3 cm,BC的垂直平分线分别交AB,BC于点D,E,则△ACD的周长为 cm.
设计意图:通过游戏环节,一方面可以调动学生学习的积极性,在他们已经疲劳之时,重新吸引其注意力:另一方面,通过练习应用新知,加深学生对知识的理解和掌握,提高学生应用新知的能力。
活动五:课堂小结
11.3 角的平分线 12.1 线段的垂直平分
性质 在角的平分线上的点到这个角的 。 性质 线段垂直平分线上的点和这条线段 。
判定 的点,在这个角的平分线上。 判定 点,在这条线段的垂直平分线上。
角的平分线是 的所有点的集合。 线段的垂直平分线是 的所有点的集合。
一条 线 一条 线
设计意图:通过本环节,将本节课所学知识做一总结,同时与角平分线的知识进行对比,在对比中提高学生对新知的理解。并将所学知识做一线街,使学生融会贯通,避免在应用过程中的混淆。渗透对比,类比思想。
活动六: 作业布置
习题13.1 6题 、9题 、
问题解决: 某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
设计意图:一方面巩固基础知识,另一方面,把学生的眼光引向生活,使生活问题数学化,提高学生应用所学知识解决实际问题的能力,进一步感受数学来源于生活有服务于生活。
l
P1
P2
B
P3
A
P
P
A
B
A
B
C
D
M
O
D
E
A
B
P
C
