2021-2022学年鲁教版(五四制)六年级数学上册3.7探索与表达规律 同步达标测评 (word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册3.7探索与表达规律 同步达标测评 (word版含解析) |

|
|
| 格式 | doc | ||
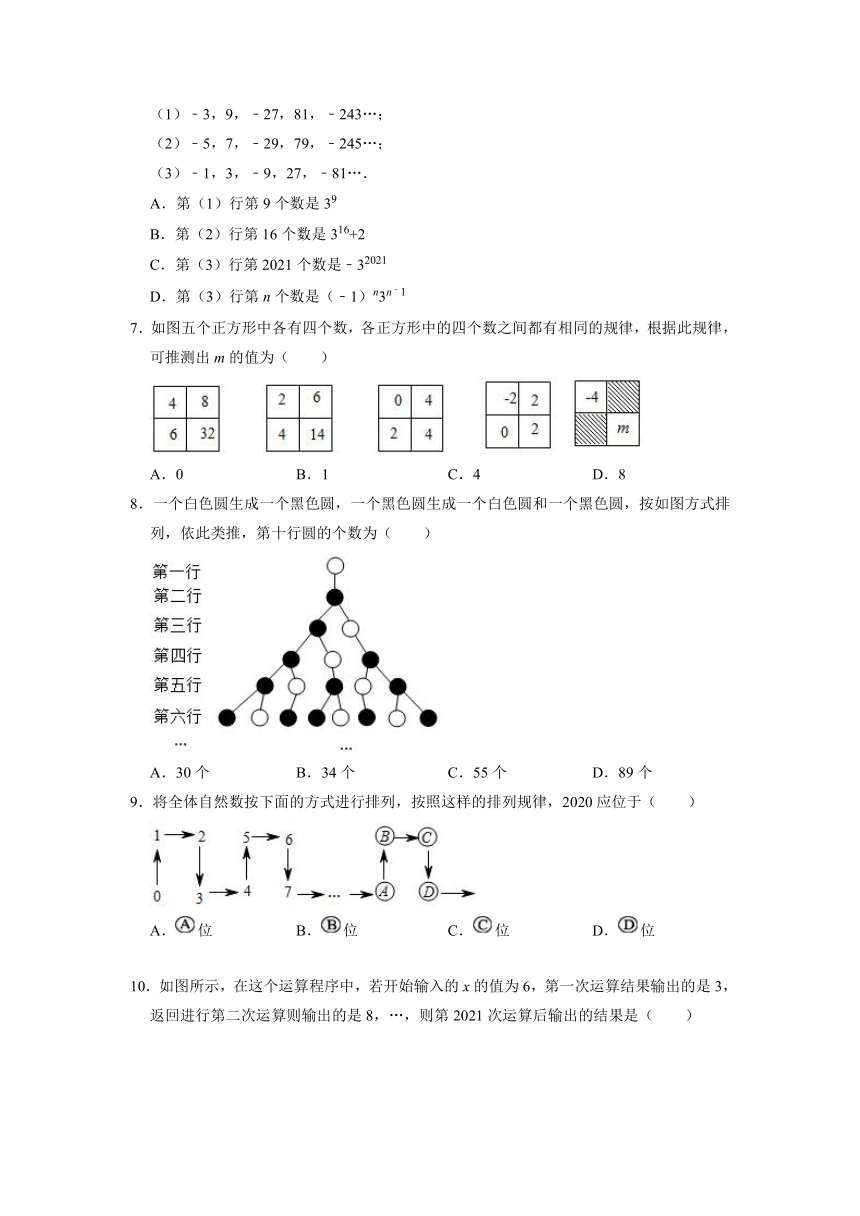
| 文件大小 | 202.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 12:19:42 | ||
图片预览


文档简介
2021-2022学年鲁教版六年级数学上册《3.7探索与表达规律》同步达标测评(附答案)
一.选择题(共10小题,满分40分)
1.观察依次排列的一串单项式x,﹣2x2,4x3,﹣8x4,16x5,…,按你发现的规律继续写下去,第8个单项式是( )
A.﹣128x7 B.﹣128x8 C.﹣256x7 D.﹣256x8
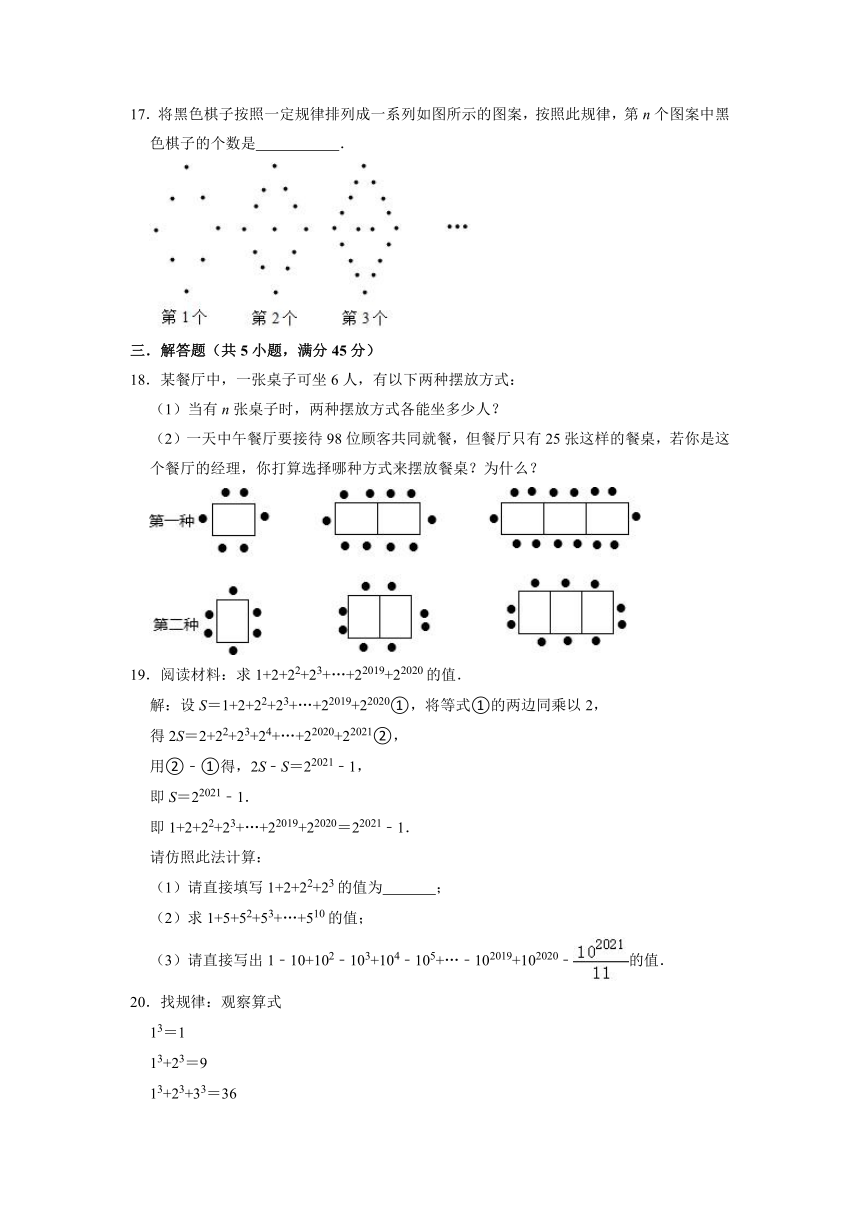
2.按规律排列的一组数据:,,□,,,,…,其中□内应填的数是( )
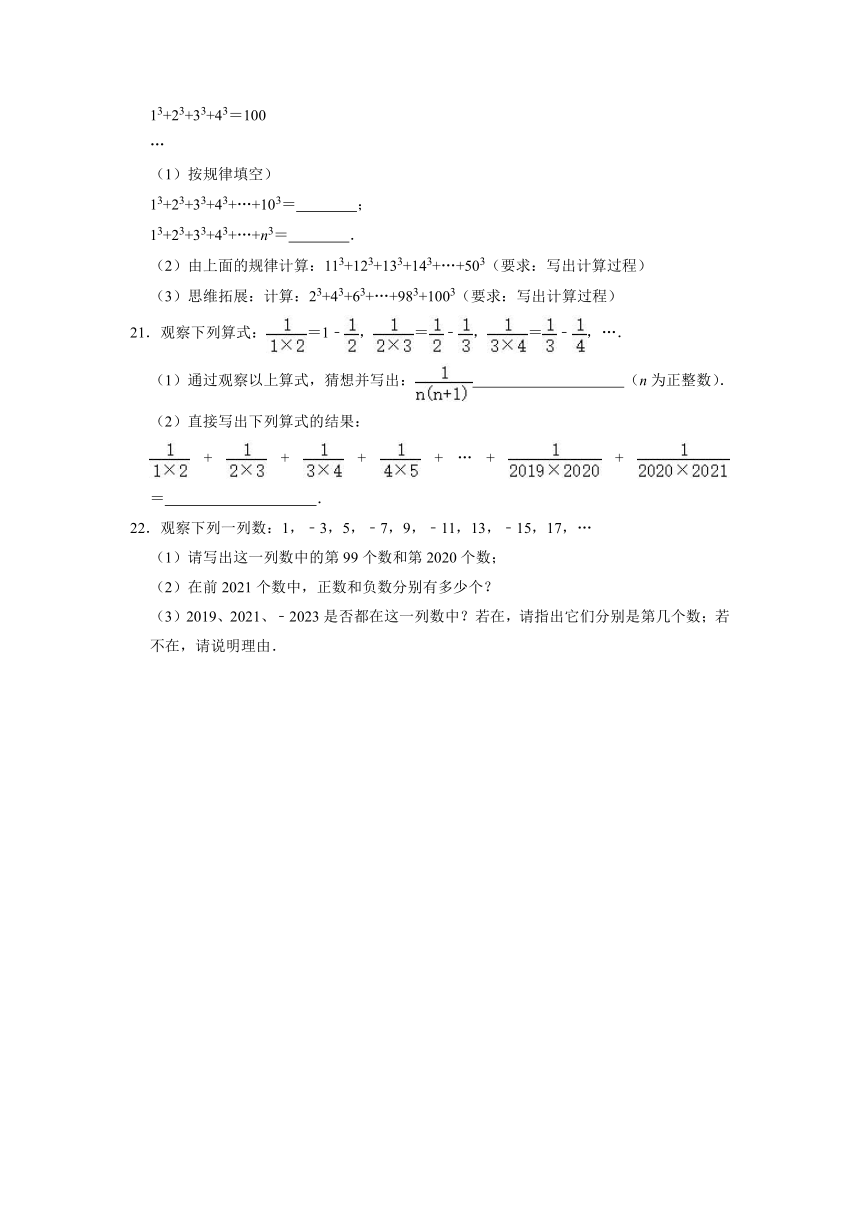
A. B. C. D.
3.将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是( )
A.2025 B.2023 C.2021 D.2019
4.根据图中数字的规律,若第n个图中的q=143,则p的值为( )
A.100 B.121 C.144 D.169
5.如图,弧长为半圆的弓形在坐标系中,圆心在(0,2).将弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为2021π时,圆心的横坐标是( )
A.2020π B.1010π+2020 C.2021π D.1011π+2020
6.某校七年级(1)班的小新同学,观察下面三行数后,用乘方的形式表示了每行数中有规律的某一个,其中正确的是( )
(1)﹣3,9,﹣27,81,﹣243…;
(2)﹣5,7,﹣29,79,﹣245…;
(3)﹣1,3,﹣9,27,﹣81….
A.第(1)行第9个数是39
B.第(2)行第16个数是316+2
C.第(3)行第2021个数是﹣32021
D.第(3)行第n个数是(﹣1)n3n﹣1
7.如图五个正方形中各有四个数,各正方形中的四个数之间都有相同的规律,根据此规律,可推测出m的值为( )
A.0 B.1 C.4 D.8
8.一个白色圆生成一个黑色圆,一个黑色圆生成一个白色圆和一个黑色圆,按如图方式排列,依此类推,第十行圆的个数为( )
A.30个 B.34个 C.55个 D.89个
9.将全体自然数按下面的方式进行排列,按照这样的排列规律,2020应位于( )
A.位 B.位 C.位 D.位
10.如图所示,在这个运算程序中,若开始输入的x的值为6,第一次运算结果输出的是3,返回进行第二次运算则输出的是8,…,则第2021次运算后输出的结果是( )
A.1 B.2 C.4 D.8
二.填空题(共7小题,满分35分)
11.如图,将正整数按此规律排列成数表,则2021是表中第 行第 列.
12.观察下列等式:1=12﹣02,3=22﹣12,5=32﹣22,…按此规律,则第n个等式为2n﹣1= .
13.将黑色圆点按如图所示的规律进行排列:
图中黑色圆点的个数依次为:1,3,6,10,…,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为 .
14.如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍;拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍;…照这样拼图,则第n个图形需要 根火柴棍.
15.观察一列数:,﹣,,﹣,…,按此规律,这一列数的第2022个数为 .
16.一组按规律排列的式子:,,,,,其中第8个式子是 ,第n个式子是 (用含的n式子表示,n为正整数).
17.将黑色棋子按照一定规律排列成一系列如图所示的图案,按照此规律,第n个图案中黑色棋子的个数是 .
三.解答题(共5小题,满分45分)
18.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
19.阅读材料:求1+2+22+23+…+22019+22020的值.
解:设S=1+2+22+23+…+22019+22020①,将等式①的两边同乘以2,
得2S=2+22+23+24+…+22020+22021②,
用②﹣①得,2S﹣S=22021﹣1,
即S=22021﹣1.
即1+2+22+23+…+22019+22020=22021﹣1.
请仿照此法计算:
(1)请直接填写1+2+22+23的值为 ;
(2)求1+5+52+53+…+510的值;
(3)请直接写出1﹣10+102﹣103+104﹣105+…﹣102019+102020﹣的值.
20.找规律:观察算式
13=1
13+23=9
13+23+33=36
13+23+33+43=100
…
(1)按规律填空)
13+23+33+43+…+103= ;
13+23+33+43+…+n3= .
(2)由上面的规律计算:113+123+133+143+…+503(要求:写出计算过程)
(3)思维拓展:计算:23+43+63+…+983+1003(要求:写出计算过程)
21.观察下列算式:=1﹣,=﹣,=﹣,….
(1)通过观察以上算式,猜想并写出: (n为正整数).
(2)直接写出下列算式的结果:
++++…++= .
22.观察下列一列数:1,﹣3,5,﹣7,9,﹣11,13,﹣15,17,…
(1)请写出这一列数中的第99个数和第2020个数;
(2)在前2021个数中,正数和负数分别有多少个?
(3)2019、2021、﹣2023是否都在这一列数中?若在,请指出它们分别是第几个数;若不在,请说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:(4x3)÷(﹣2x2)=﹣2x,
(﹣8x4)÷(4x3)=﹣2x,
(16x5)÷(﹣8x4)=﹣2x,
…
所以从第二个单项式起,每一个单项式与它前面的单项式的商都是﹣2x;
按发现的规律可知:
x,﹣2x2,
4x3=22x3,
﹣8x4=﹣23x4,
16x5=24x5,
…
所以第8个单项式是﹣27x8=﹣128x8.
故选:B.
2.解:观察这排数据发现:分子为连续的奇数,分母为序号的平方+1,
∴第n个数据为:.
当n=3时,□的分子为5,分母=32+1=10,
∴这个数为=,
故选:D.
3.解:由题意可知:
行数为1的方阵内包含“1”,共1个数;
行数为2的方阵内包含“1、3、5、7”,共22个数;
行数为3的方阵内包含“1、3、5、7、9、11、13、15、17”,共32个数;
∴行数为32的方阵内包含“1、3、5、7、......”共322个数,即共1024个数,
∴位于第32行第13列的数是连续奇数的第(1024﹣12)=1012个数,
∴位于第32行第13列的数是:2×1012﹣1=2023.
故选:B.
4.解:通过观察可得规律:p=n2,q=(n+1)2﹣1,
∵q=143,
∴(n+1)2﹣1=143,
解得:n=11,
∴p=n2=112=121,
故选:B.
5.解:由题知,图形每旋转一周,圆心的路径循环一次,且路径长度刚好为以2为半径的圆的周长,
即4π,
2021π÷4π=505(圈),
即当圆心经过的路径长为2021π时,图形旋转了505圈,
∵图形每旋转一圈横坐标增加2π+4,
∴当图形旋转505圈时的横坐标为(2π+4)×505=1010π+2020,
再转圈横坐标增加×4π=π,
∴当圆心经过的路径长为2021π时,圆心的横坐标是1010π+2020+π=1011π+2020,
故选:D.
6.解:(1)﹣3,9,﹣27,81,﹣243…;
∴第n个数为:(﹣1)n×3n,
∴第(1)行第9个数是﹣39,
故A错;
(2)﹣5,7,﹣29,79,﹣245…;
∴第n个数为:(﹣1)n×3n﹣2,
∴第(2)行第16个数是316﹣2,
故B错;
(3)﹣1,3,﹣9,27,﹣81…;
∴第n个数为:(﹣1)n3n﹣1,
∴第(3)行第2021个数是﹣32020,
故C错D对;
故选:D.
7.解:由前四个正方形内数的规律可知:
每个正方形左上、左下、右上三个数是连续的三个偶数,
故第五个正方形左下和右上两数分别为:﹣2,0.
而每个正方形右下的数=左上的数×左下的数+右上的数,
故m=(﹣4)×(﹣2)+0=8.
故选:D.
8.解:由题意知前六行圆数为:1,1,2,3,5,8,
即从第三行开始圆数为前两行圆数之和,
∴第七行为:13,
第八行为:21,
第九行为:34,
第十行为:55,
故选:C.
9.解:由图可知,每4个数为一个循环组依次循环,
∵2020是第2021个数,
∴2021÷4=505余1,
∴2020应位于第506循环组的第1个数,在A位.
故选:A.
10.解:根据题意第一次运算结果输出的是3,
第二次运算输出的是8,
第三次运算输出的是4,
第四次运算输出的是2,
第五次运算输出的是1,
第六次运算输出的是6,
第七次运算输出的是3,
第八次运算输出的是8,
第九次运算输出的是4,
第十次运算输出的是2,
...
以上可以看出每6次输出的结果就会循环,
∵2021÷6=336......5,
∴第2021次输出的结果和第5次一样为1,
故选:A.
二.填空题(共7小题,满分35分)
11.解:由图可知,
第一行1个数字,
第二行2个数字,
第三行3个数字,
…,
则第n行n个数字,
前n行一共有个数字,
∵<2021<,2021﹣=2021﹣2016=5,
∴2021是表中第64行第5列,
故答案为:64,5.
12.解:∵1=12﹣02,3=22﹣12,5=32﹣22,…,
∴第n个等式为2n﹣1=n2﹣(n﹣1)2,
故答案为:n2﹣(n﹣1)2.
13.解:第①个图形中的黑色圆点的个数为:1,
第②个图形中的黑色圆点的个数为:=3,
第③个图形中的黑色圆点的个数为:=6,
第④个图形中的黑色圆点的个数为:=10,
…
第n个图形中的黑色圆点的个数为,
则这列数为1,3,6,10,15,21,28,36,45,55,66,78,91,…,
其中每3个数中,都有2个能被3整除,
33÷2=16…1,
16×3+2=50,
则第33个被3整除的数为原数列中第50个数,即=1275,
故答案为:1275.
14.解:设第n个图形需要an(n为正整数)根火柴棒,
观察发现规律:第一个图形需要火柴棍:3=1×2+1,
第二个图形需要火柴棍:5=2×2+1;
第三个图形需要火柴棍:7=3×2+1,…,
∴第n个图形需要火柴棍:2n+1.
故答案为:(2n+1).
15.解:观察一列数:,﹣,,﹣,…,
根据规律可知,
第n个数为(﹣1)n+1(),
∴第2022个数是﹣,
故答案为:﹣.
16.解:∵=(﹣1)2 ,
﹣=(﹣1)3 ,
=(﹣1)4 ,
…
∴第8个式子是,
第n个式子为:(﹣1)n+1 .
故答案是:;(﹣1)n+1 .
17.解:观察图形的变化可知:
第1个图案中黑色棋子的个数是8=5×1+3;
第2个图案中黑色棋子的个数是13=5×2+3
第3个图案中黑色棋子的个数是18=5×3+3
…
发现规律:
第n个图案中黑色棋子的个数是(5n+3).
故答案为:(5n+3).
三.解答题(共5小题,满分45分)
18.解:(1)第一种中,只有一张桌子是6人,后边多一张桌子多4人.即有n张桌子时是6+4(n﹣1)=4n+2.
第二种中,有一张桌子是6人,后边多一张桌子多2人,即6+2(n﹣1)=2n+4.
(2)中,分别求出两种对应的n的值,或分别求出n=25时,两种不同的摆放方式对应的人数,即可作出判断.
打算用第一种摆放方式来摆放餐桌.
因为,当n=25时,4×25+2=102>98
当n=25时,2×25+4=54<98
所以,选用第一种摆放方式.
19.解:(1)1+2+22+23
=1+2+4+8
=15,
故答案为:15;
(2)设S=1+5+52+53+…+510,
则5S=5+52+53+…+511,
∴5S﹣S=511﹣1,
∴4S=511﹣1,
∴S=,
即1+5+52+53+…+510=;
(3)设S=1﹣10+102﹣103+104﹣105+…﹣102019+102020,
则10S=10﹣102+103﹣104+105﹣…﹣102020+102021,
∴S+10S=1+102021,
∴11S=1+102021,
∴S=,
∴1﹣10+102﹣103+104﹣105+…﹣102019+102020﹣
=﹣
=.
20.解:(1)13+23+33+43+…+103=(1+2+3+4+…+10)2=[]2=552;
13+23+33+43+…+n3=(1+2+3+4+…+n)2=;
(2)113+123+133+143+…+503=(13+23+33+43+…+503)﹣(13+23+33+43+…+103)=[]2﹣[]2=1622600;
(3)23+43+63+…+983+1003=(2×1)3+(2×2)3+(2×3)2+(2×4)3+…+(2×50)3=23×(13+23+33+43+…+503)=23×[]2=8×12752.
故答案为:552;.
21.解:(1)由题意可得,
=,
故答案为:=;
(2)++++…++
=1﹣++…+
=1﹣
=,
故答案为:.
22.解:(1)通过观察可得:数字的绝对值的规律是奇数为2n﹣1,符号规律为正负交替,第奇数个为正号,第偶数个为负号,
∴第99个数为2×99﹣1=197,第2020个数为﹣(2×2020﹣1)=﹣4039.
(2)在前2021个数中,正数有1011个,负数有1010个.
(3)2019不在这列数中,2021、﹣2023在这一列数中,
∵2019=2n﹣1,
∴n=1010,第偶数个应该为负号,
故2019不在这列数中,
∵2021=2n﹣1,
∴n=1011,第奇数个为正号,
故2021在这列数中,
∵2023=2n﹣1,
∴n=1012,第偶数个应该为负号,
故﹣2023在这列数中.
一.选择题(共10小题,满分40分)
1.观察依次排列的一串单项式x,﹣2x2,4x3,﹣8x4,16x5,…,按你发现的规律继续写下去,第8个单项式是( )
A.﹣128x7 B.﹣128x8 C.﹣256x7 D.﹣256x8
2.按规律排列的一组数据:,,□,,,,…,其中□内应填的数是( )
A. B. C. D.
3.将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是( )
A.2025 B.2023 C.2021 D.2019
4.根据图中数字的规律,若第n个图中的q=143,则p的值为( )
A.100 B.121 C.144 D.169
5.如图,弧长为半圆的弓形在坐标系中,圆心在(0,2).将弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为2021π时,圆心的横坐标是( )
A.2020π B.1010π+2020 C.2021π D.1011π+2020
6.某校七年级(1)班的小新同学,观察下面三行数后,用乘方的形式表示了每行数中有规律的某一个,其中正确的是( )
(1)﹣3,9,﹣27,81,﹣243…;
(2)﹣5,7,﹣29,79,﹣245…;
(3)﹣1,3,﹣9,27,﹣81….
A.第(1)行第9个数是39
B.第(2)行第16个数是316+2
C.第(3)行第2021个数是﹣32021
D.第(3)行第n个数是(﹣1)n3n﹣1
7.如图五个正方形中各有四个数,各正方形中的四个数之间都有相同的规律,根据此规律,可推测出m的值为( )
A.0 B.1 C.4 D.8
8.一个白色圆生成一个黑色圆,一个黑色圆生成一个白色圆和一个黑色圆,按如图方式排列,依此类推,第十行圆的个数为( )
A.30个 B.34个 C.55个 D.89个
9.将全体自然数按下面的方式进行排列,按照这样的排列规律,2020应位于( )
A.位 B.位 C.位 D.位
10.如图所示,在这个运算程序中,若开始输入的x的值为6,第一次运算结果输出的是3,返回进行第二次运算则输出的是8,…,则第2021次运算后输出的结果是( )
A.1 B.2 C.4 D.8
二.填空题(共7小题,满分35分)
11.如图,将正整数按此规律排列成数表,则2021是表中第 行第 列.
12.观察下列等式:1=12﹣02,3=22﹣12,5=32﹣22,…按此规律,则第n个等式为2n﹣1= .
13.将黑色圆点按如图所示的规律进行排列:
图中黑色圆点的个数依次为:1,3,6,10,…,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为 .
14.如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍;拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍;…照这样拼图,则第n个图形需要 根火柴棍.
15.观察一列数:,﹣,,﹣,…,按此规律,这一列数的第2022个数为 .
16.一组按规律排列的式子:,,,,,其中第8个式子是 ,第n个式子是 (用含的n式子表示,n为正整数).
17.将黑色棋子按照一定规律排列成一系列如图所示的图案,按照此规律,第n个图案中黑色棋子的个数是 .
三.解答题(共5小题,满分45分)
18.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
19.阅读材料:求1+2+22+23+…+22019+22020的值.
解:设S=1+2+22+23+…+22019+22020①,将等式①的两边同乘以2,
得2S=2+22+23+24+…+22020+22021②,
用②﹣①得,2S﹣S=22021﹣1,
即S=22021﹣1.
即1+2+22+23+…+22019+22020=22021﹣1.
请仿照此法计算:
(1)请直接填写1+2+22+23的值为 ;
(2)求1+5+52+53+…+510的值;
(3)请直接写出1﹣10+102﹣103+104﹣105+…﹣102019+102020﹣的值.
20.找规律:观察算式
13=1
13+23=9
13+23+33=36
13+23+33+43=100
…
(1)按规律填空)
13+23+33+43+…+103= ;
13+23+33+43+…+n3= .
(2)由上面的规律计算:113+123+133+143+…+503(要求:写出计算过程)
(3)思维拓展:计算:23+43+63+…+983+1003(要求:写出计算过程)
21.观察下列算式:=1﹣,=﹣,=﹣,….
(1)通过观察以上算式,猜想并写出: (n为正整数).
(2)直接写出下列算式的结果:
++++…++= .
22.观察下列一列数:1,﹣3,5,﹣7,9,﹣11,13,﹣15,17,…
(1)请写出这一列数中的第99个数和第2020个数;
(2)在前2021个数中,正数和负数分别有多少个?
(3)2019、2021、﹣2023是否都在这一列数中?若在,请指出它们分别是第几个数;若不在,请说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:(4x3)÷(﹣2x2)=﹣2x,
(﹣8x4)÷(4x3)=﹣2x,
(16x5)÷(﹣8x4)=﹣2x,
…
所以从第二个单项式起,每一个单项式与它前面的单项式的商都是﹣2x;
按发现的规律可知:
x,﹣2x2,
4x3=22x3,
﹣8x4=﹣23x4,
16x5=24x5,
…
所以第8个单项式是﹣27x8=﹣128x8.
故选:B.
2.解:观察这排数据发现:分子为连续的奇数,分母为序号的平方+1,
∴第n个数据为:.
当n=3时,□的分子为5,分母=32+1=10,
∴这个数为=,
故选:D.
3.解:由题意可知:
行数为1的方阵内包含“1”,共1个数;
行数为2的方阵内包含“1、3、5、7”,共22个数;
行数为3的方阵内包含“1、3、5、7、9、11、13、15、17”,共32个数;
∴行数为32的方阵内包含“1、3、5、7、......”共322个数,即共1024个数,
∴位于第32行第13列的数是连续奇数的第(1024﹣12)=1012个数,
∴位于第32行第13列的数是:2×1012﹣1=2023.
故选:B.
4.解:通过观察可得规律:p=n2,q=(n+1)2﹣1,
∵q=143,
∴(n+1)2﹣1=143,
解得:n=11,
∴p=n2=112=121,
故选:B.
5.解:由题知,图形每旋转一周,圆心的路径循环一次,且路径长度刚好为以2为半径的圆的周长,
即4π,
2021π÷4π=505(圈),
即当圆心经过的路径长为2021π时,图形旋转了505圈,
∵图形每旋转一圈横坐标增加2π+4,
∴当图形旋转505圈时的横坐标为(2π+4)×505=1010π+2020,
再转圈横坐标增加×4π=π,
∴当圆心经过的路径长为2021π时,圆心的横坐标是1010π+2020+π=1011π+2020,
故选:D.
6.解:(1)﹣3,9,﹣27,81,﹣243…;
∴第n个数为:(﹣1)n×3n,
∴第(1)行第9个数是﹣39,
故A错;
(2)﹣5,7,﹣29,79,﹣245…;
∴第n个数为:(﹣1)n×3n﹣2,
∴第(2)行第16个数是316﹣2,
故B错;
(3)﹣1,3,﹣9,27,﹣81…;
∴第n个数为:(﹣1)n3n﹣1,
∴第(3)行第2021个数是﹣32020,
故C错D对;
故选:D.
7.解:由前四个正方形内数的规律可知:
每个正方形左上、左下、右上三个数是连续的三个偶数,
故第五个正方形左下和右上两数分别为:﹣2,0.
而每个正方形右下的数=左上的数×左下的数+右上的数,
故m=(﹣4)×(﹣2)+0=8.
故选:D.
8.解:由题意知前六行圆数为:1,1,2,3,5,8,
即从第三行开始圆数为前两行圆数之和,
∴第七行为:13,
第八行为:21,
第九行为:34,
第十行为:55,
故选:C.
9.解:由图可知,每4个数为一个循环组依次循环,
∵2020是第2021个数,
∴2021÷4=505余1,
∴2020应位于第506循环组的第1个数,在A位.
故选:A.
10.解:根据题意第一次运算结果输出的是3,
第二次运算输出的是8,
第三次运算输出的是4,
第四次运算输出的是2,
第五次运算输出的是1,
第六次运算输出的是6,
第七次运算输出的是3,
第八次运算输出的是8,
第九次运算输出的是4,
第十次运算输出的是2,
...
以上可以看出每6次输出的结果就会循环,
∵2021÷6=336......5,
∴第2021次输出的结果和第5次一样为1,
故选:A.
二.填空题(共7小题,满分35分)
11.解:由图可知,
第一行1个数字,
第二行2个数字,
第三行3个数字,
…,
则第n行n个数字,
前n行一共有个数字,
∵<2021<,2021﹣=2021﹣2016=5,
∴2021是表中第64行第5列,
故答案为:64,5.
12.解:∵1=12﹣02,3=22﹣12,5=32﹣22,…,
∴第n个等式为2n﹣1=n2﹣(n﹣1)2,
故答案为:n2﹣(n﹣1)2.
13.解:第①个图形中的黑色圆点的个数为:1,
第②个图形中的黑色圆点的个数为:=3,
第③个图形中的黑色圆点的个数为:=6,
第④个图形中的黑色圆点的个数为:=10,
…
第n个图形中的黑色圆点的个数为,
则这列数为1,3,6,10,15,21,28,36,45,55,66,78,91,…,
其中每3个数中,都有2个能被3整除,
33÷2=16…1,
16×3+2=50,
则第33个被3整除的数为原数列中第50个数,即=1275,
故答案为:1275.
14.解:设第n个图形需要an(n为正整数)根火柴棒,
观察发现规律:第一个图形需要火柴棍:3=1×2+1,
第二个图形需要火柴棍:5=2×2+1;
第三个图形需要火柴棍:7=3×2+1,…,
∴第n个图形需要火柴棍:2n+1.
故答案为:(2n+1).
15.解:观察一列数:,﹣,,﹣,…,
根据规律可知,
第n个数为(﹣1)n+1(),
∴第2022个数是﹣,
故答案为:﹣.
16.解:∵=(﹣1)2 ,
﹣=(﹣1)3 ,
=(﹣1)4 ,
…
∴第8个式子是,
第n个式子为:(﹣1)n+1 .
故答案是:;(﹣1)n+1 .
17.解:观察图形的变化可知:
第1个图案中黑色棋子的个数是8=5×1+3;
第2个图案中黑色棋子的个数是13=5×2+3
第3个图案中黑色棋子的个数是18=5×3+3
…
发现规律:
第n个图案中黑色棋子的个数是(5n+3).
故答案为:(5n+3).
三.解答题(共5小题,满分45分)
18.解:(1)第一种中,只有一张桌子是6人,后边多一张桌子多4人.即有n张桌子时是6+4(n﹣1)=4n+2.
第二种中,有一张桌子是6人,后边多一张桌子多2人,即6+2(n﹣1)=2n+4.
(2)中,分别求出两种对应的n的值,或分别求出n=25时,两种不同的摆放方式对应的人数,即可作出判断.
打算用第一种摆放方式来摆放餐桌.
因为,当n=25时,4×25+2=102>98
当n=25时,2×25+4=54<98
所以,选用第一种摆放方式.
19.解:(1)1+2+22+23
=1+2+4+8
=15,
故答案为:15;
(2)设S=1+5+52+53+…+510,
则5S=5+52+53+…+511,
∴5S﹣S=511﹣1,
∴4S=511﹣1,
∴S=,
即1+5+52+53+…+510=;
(3)设S=1﹣10+102﹣103+104﹣105+…﹣102019+102020,
则10S=10﹣102+103﹣104+105﹣…﹣102020+102021,
∴S+10S=1+102021,
∴11S=1+102021,
∴S=,
∴1﹣10+102﹣103+104﹣105+…﹣102019+102020﹣
=﹣
=.
20.解:(1)13+23+33+43+…+103=(1+2+3+4+…+10)2=[]2=552;
13+23+33+43+…+n3=(1+2+3+4+…+n)2=;
(2)113+123+133+143+…+503=(13+23+33+43+…+503)﹣(13+23+33+43+…+103)=[]2﹣[]2=1622600;
(3)23+43+63+…+983+1003=(2×1)3+(2×2)3+(2×3)2+(2×4)3+…+(2×50)3=23×(13+23+33+43+…+503)=23×[]2=8×12752.
故答案为:552;.
21.解:(1)由题意可得,
=,
故答案为:=;
(2)++++…++
=1﹣++…+
=1﹣
=,
故答案为:.
22.解:(1)通过观察可得:数字的绝对值的规律是奇数为2n﹣1,符号规律为正负交替,第奇数个为正号,第偶数个为负号,
∴第99个数为2×99﹣1=197,第2020个数为﹣(2×2020﹣1)=﹣4039.
(2)在前2021个数中,正数有1011个,负数有1010个.
(3)2019不在这列数中,2021、﹣2023在这一列数中,
∵2019=2n﹣1,
∴n=1010,第偶数个应该为负号,
故2019不在这列数中,
∵2021=2n﹣1,
∴n=1011,第奇数个为正号,
故2021在这列数中,
∵2023=2n﹣1,
∴n=1012,第偶数个应该为负号,
故﹣2023在这列数中.
