26.3 用频率估计概率 课件(共16张PPT)
文档属性
| 名称 | 26.3 用频率估计概率 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 198.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 06:12:33 | ||
图片预览






文档简介
(共16张PPT)
第二十六章 概率初步
26.3 用频率估计概率
1.理解并掌握用随机事件的频率估计概率的原理. (重点)
2.理解频率与概率的关系,并能运用其进行简单计算.(难点)
学习目标
新课导入
情境导入
小明抛掷一枚硬币10次,其正面朝上的次数为5次,是否可以说明“正面向上”这一事件发生的概率为0.5?
实际上,我们还可以利用多次重复试验,通过统计试验结果估计概率.
新课讲解
知识点1 用频率估计概率
合作探究
问题一 一位同学在做“抛硬币”的试验中,将获得的数据绘制成下表及折线统计图,其中:
出现正面的频率=
出现正面次数
抛掷次数
抛掷次数 50 100 200 300 400 500 600 700 800
出现正面次数 25 52 95 145 195 243 295 345 396
出现正面的频率 0.500 0.520 0.475 0.483 0.488 0.486 0.492 0.493 0.495
新课讲解
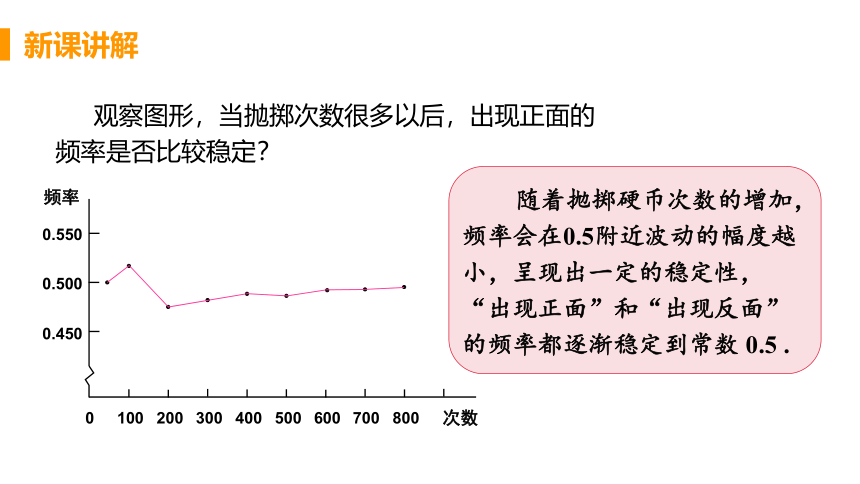
观察图形,当抛掷次数很多以后,出现正面的频率是否比较稳定?
0
100
200
300
400
500
600
700
800
次数
频率
0.450
0.500
0.550
随着抛掷硬币次数的增加,频率会在0.5附近波动的幅度越小,呈现出一定的稳定性,“出现正面”和“出现反面”的频率都逐渐稳定到常数 0.5 .
新课讲解
问题二 某农科所通过抽样试验来估计一大批种子(总体)的发芽率,为此,从中抽取10批,分别做发芽试验,记录下每批发芽粒数,并算出发芽的频率(发芽粒数与每批试验例数之比),结果如下表:
每批试验粒数n 2 5 10 70 130 310 700 1500 2000 3000
发芽粒数m 2 4 9 60 116 282 639 1339 1806 2715
发芽的频率 1 0.800 0.900 0.857 0.892 0.910 0.913 0.893 0.903 0.905
由上面试验所得数据可以看出:当发芽试验样本容量增大时,发芽的频率逐渐稳定到常数0.9.
新课讲解
结论
一般地,在大量重复试验下,随机事件A发生的频率会稳定到某个常数p.于是,我们用p这个常数表示随机事件A发生的概率,即
p(A)=
m
n
新课讲解
例
典例分析
1 一个不透明的口袋中放有若干个红球和白球,这两种球除了颜色以外没有其他区别,将袋中的球摇均匀.每次从口袋中取出一个球记录颜色后放回再摇均匀,经过大量的试验,得到取出红球的频率是
(1)估计取出白球的概率是多少?
(2)如果袋中的白球有18个,那么袋中的红球约有多 少个?
新课讲解
(1)对于非A即B的两个事件,其概率之和为1;
(2)列出方程求解.
(1)∵取出红球的频率是
∴取出红球的概率约是
∴估计取出白球的概率为
(2)设袋中的红球有x个,根据题意,得
解得x≈6.
∴袋中的红球约有6个.
分析:
解:
课堂小结
大量重复
试验
事件发生的可能性
发生结果等可能
发生结果不等可能
频率值逐渐稳定
概率
转化成数学问题
1.频率与概率的区别与联系
2.用频率估计事件发生的概率
3.用替代物进行模拟试验
当堂小练
1.在大量重复试验中,关于随机事件发生的频率与概
率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
当堂小练
2.某小组做“用频率估计概率”的试验时,统计了某一结果出现的
频率,绘制了如图的折线统计图,则符合这一结果的试验最有
可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一枚质地均匀的正六面体骰子,向上的面点数是4
D
当堂小练
4.在一个不透明的口袋里,装有仅颜色不同的黑球、白球
若干个,某小组做摸球试验:将球搅匀后从中随机摸出
一个,记下颜色,再放入袋中,不断重复,下表是活动
中的一组数据,则摸到白球的概率约是( )
A.0.4 B.0.5 C.0.6 D.0.7
C
D
拓展与延伸
在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1 000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
拓展与延伸
(1)请估计:当n很大时,摸到白球的频率将会接近
________(精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是________,摸
到黑球的概率是________.
(3)试估算口袋中黑、白两种颜色的球各有多少个?
0.6
0.6
0.4
(4)解决了上面的问题,小明同学猛然顿悟,过去一个悬而未
决的问题有办法解决了.这个问题是:在一个不透明的口
袋里装有若干个白球,在不允许将球倒出来数的情况下,
(3)白球有20×0.6=12(个),黑球有20-12=8(个).
解:
(4) 把a个黑球装入口袋中,将黑球、白球混合搅匀,做摸球试验,随机摸出一个球记下颜色,再放回口袋中,不断重复,可得到摸到黑球的频率,从而估计出摸到黑球的概率为P,由于黑球有a个,则设白球的数量为b,得 解得
如何估计白球的个数?请你应用统计与概率的思想和方法
解决这个问题,写出解决这个问题的主要步骤及估算方法
(可以借助其他工具及用品).
拓展与延伸
第二十六章 概率初步
26.3 用频率估计概率
1.理解并掌握用随机事件的频率估计概率的原理. (重点)
2.理解频率与概率的关系,并能运用其进行简单计算.(难点)
学习目标
新课导入
情境导入
小明抛掷一枚硬币10次,其正面朝上的次数为5次,是否可以说明“正面向上”这一事件发生的概率为0.5?
实际上,我们还可以利用多次重复试验,通过统计试验结果估计概率.
新课讲解
知识点1 用频率估计概率
合作探究
问题一 一位同学在做“抛硬币”的试验中,将获得的数据绘制成下表及折线统计图,其中:
出现正面的频率=
出现正面次数
抛掷次数
抛掷次数 50 100 200 300 400 500 600 700 800
出现正面次数 25 52 95 145 195 243 295 345 396
出现正面的频率 0.500 0.520 0.475 0.483 0.488 0.486 0.492 0.493 0.495
新课讲解
观察图形,当抛掷次数很多以后,出现正面的频率是否比较稳定?
0
100
200
300
400
500
600
700
800
次数
频率
0.450
0.500
0.550
随着抛掷硬币次数的增加,频率会在0.5附近波动的幅度越小,呈现出一定的稳定性,“出现正面”和“出现反面”的频率都逐渐稳定到常数 0.5 .
新课讲解
问题二 某农科所通过抽样试验来估计一大批种子(总体)的发芽率,为此,从中抽取10批,分别做发芽试验,记录下每批发芽粒数,并算出发芽的频率(发芽粒数与每批试验例数之比),结果如下表:
每批试验粒数n 2 5 10 70 130 310 700 1500 2000 3000
发芽粒数m 2 4 9 60 116 282 639 1339 1806 2715
发芽的频率 1 0.800 0.900 0.857 0.892 0.910 0.913 0.893 0.903 0.905
由上面试验所得数据可以看出:当发芽试验样本容量增大时,发芽的频率逐渐稳定到常数0.9.
新课讲解
结论
一般地,在大量重复试验下,随机事件A发生的频率会稳定到某个常数p.于是,我们用p这个常数表示随机事件A发生的概率,即
p(A)=
m
n
新课讲解
例
典例分析
1 一个不透明的口袋中放有若干个红球和白球,这两种球除了颜色以外没有其他区别,将袋中的球摇均匀.每次从口袋中取出一个球记录颜色后放回再摇均匀,经过大量的试验,得到取出红球的频率是
(1)估计取出白球的概率是多少?
(2)如果袋中的白球有18个,那么袋中的红球约有多 少个?
新课讲解
(1)对于非A即B的两个事件,其概率之和为1;
(2)列出方程求解.
(1)∵取出红球的频率是
∴取出红球的概率约是
∴估计取出白球的概率为
(2)设袋中的红球有x个,根据题意,得
解得x≈6.
∴袋中的红球约有6个.
分析:
解:
课堂小结
大量重复
试验
事件发生的可能性
发生结果等可能
发生结果不等可能
频率值逐渐稳定
概率
转化成数学问题
1.频率与概率的区别与联系
2.用频率估计事件发生的概率
3.用替代物进行模拟试验
当堂小练
1.在大量重复试验中,关于随机事件发生的频率与概
率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
当堂小练
2.某小组做“用频率估计概率”的试验时,统计了某一结果出现的
频率,绘制了如图的折线统计图,则符合这一结果的试验最有
可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一枚质地均匀的正六面体骰子,向上的面点数是4
D
当堂小练
4.在一个不透明的口袋里,装有仅颜色不同的黑球、白球
若干个,某小组做摸球试验:将球搅匀后从中随机摸出
一个,记下颜色,再放入袋中,不断重复,下表是活动
中的一组数据,则摸到白球的概率约是( )
A.0.4 B.0.5 C.0.6 D.0.7
C
D
拓展与延伸
在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1 000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
拓展与延伸
(1)请估计:当n很大时,摸到白球的频率将会接近
________(精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是________,摸
到黑球的概率是________.
(3)试估算口袋中黑、白两种颜色的球各有多少个?
0.6
0.6
0.4
(4)解决了上面的问题,小明同学猛然顿悟,过去一个悬而未
决的问题有办法解决了.这个问题是:在一个不透明的口
袋里装有若干个白球,在不允许将球倒出来数的情况下,
(3)白球有20×0.6=12(个),黑球有20-12=8(个).
解:
(4) 把a个黑球装入口袋中,将黑球、白球混合搅匀,做摸球试验,随机摸出一个球记下颜色,再放回口袋中,不断重复,可得到摸到黑球的频率,从而估计出摸到黑球的概率为P,由于黑球有a个,则设白球的数量为b,得 解得
如何估计白球的个数?请你应用统计与概率的思想和方法
解决这个问题,写出解决这个问题的主要步骤及估算方法
(可以借助其他工具及用品).
拓展与延伸
