26.4 综合与实践 概率在遗传学中的应用 课件(共23张PPT)
文档属性
| 名称 | 26.4 综合与实践 概率在遗传学中的应用 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 421.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第二十六章 概率初步
26.2 等可能情形下的概率计算
第1课时 利用概率公式求概率
1.了解概率在遗传学中的应用. (重点)
2.掌握几何概率的计算和应用.(难点)
学习目标
新课导入
情境导入
读一读下列俗语:
龙生龙,凤生凤,老鼠生儿会打洞.
虎父无犬子.
桂实生桂,桐实生桐.
种瓜得瓜,种豆得豆.
种豆其苗必豆,种瓜其苗必瓜.
这些俗语反映了什么现象?
新课讲解
知识点1 概率在遗传学中的应用
双亲的遗传物质混合后,子代的性状介于双亲之间.
答:品红色(介于红色和蓝色之间)
答:不能
问题一 红墨水与蓝墨水混合后的颜色?
问题二 混合后能否再将这两种墨水分开?
问题三 那么遗传是这样吗?
合作探究
新课讲解
想一想:为什么用豌豆做实验材料容易成功?
豌豆花特点:自花传粉,闭花授粉
纯种
自然状态下,一般都是
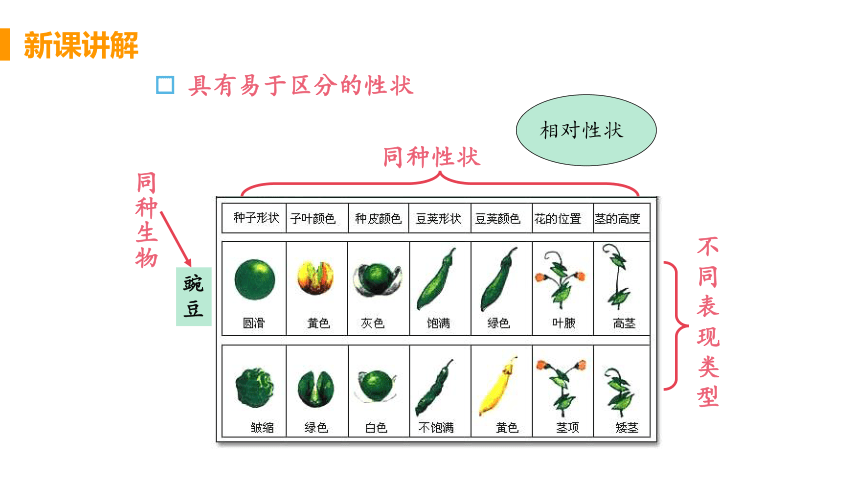
具有易于区分的性状
豌豆
同种生物
同种性状
不同表现类型
相对性状
新课讲解
遗传学中把生物体所表现的形态结构、生理特征和行为方式等统称为性状.如:豌豆的花色、种子形状、子叶颜色、茎的高矮等都可以称之为性状.
新课讲解
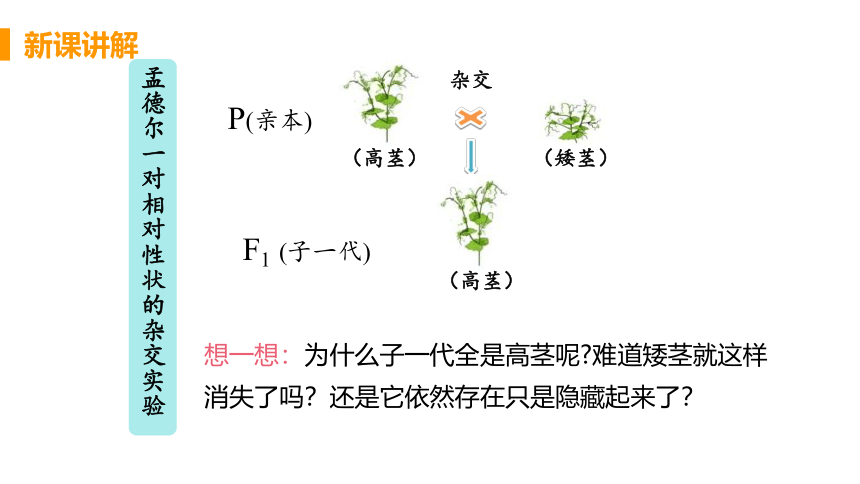
(高茎)
(矮茎)
P(亲本)
F1 (子一代)
(高茎)
孟德尔一对相对性状的杂交实验
想一想:为什么子一代全是高茎呢 难道矮茎就这样消失了吗?还是它依然存在只是隐藏起来了?
杂交
新课讲解
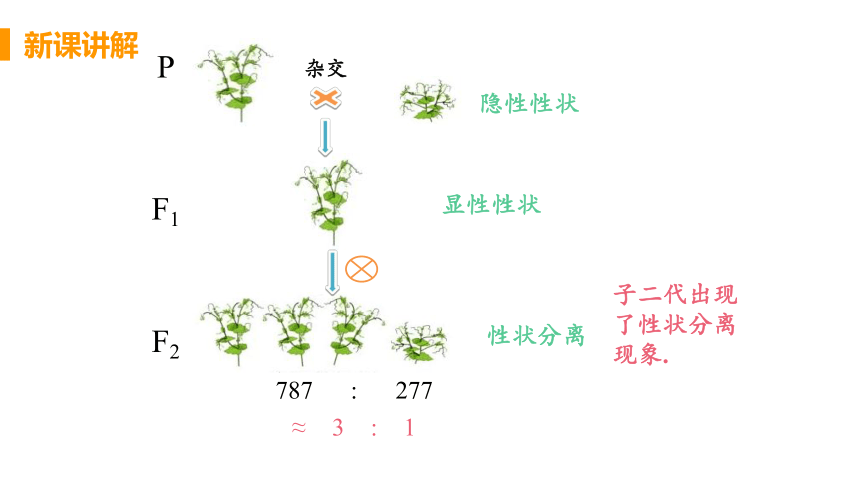
787 : 277
P
F1
F2
≈3:1
显性性状
隐性性状
性状分离
子二代出现了性状分离现象.
杂交
新课讲解
高茎豌豆和矮茎豌豆杂交实验的分析图解
Aa
×
A
a
A
a
AA
Aa
Aa
aa
AA
×
aa
高茎
矮茎
P
配子
Aa
F1
A
a
配子
F2
高茎
高茎
高茎
矮茎
新课讲解
新课讲解
例
典例分析
1 白化病是一种隐性的性状,如果N是正常的基因,a是白化病基因,那么携带一对基因Na的个体的皮肤,头发和眼球的颜色是正常的,而携带一对基因aa的个体将患有白化病.
(1)设母亲和父亲都携带成对基因Na,求他们有正常孩子的概率;
P(有正常孩子)=
(2)设母亲和父亲分别携带一对基因NN和Na,求他们有
正常孩子的概率和孩子患白血病的概率;
NN
Na
N
a
NN
Na
NN
Na
N
N
正常
正常
正常
正常
P(有正常孩子)=
P(孩子患白血病)=
新课讲解
(3)设母亲和父亲分别携带一对基因aa和Na,求他们有正常
孩子的概率和孩子患白血病的概率.
aa
Na
N
a
Na
aa
Na
aa
a
a
正常
白血病
正常
白血病
P(有正常孩子)=
P(孩子患白血病)=
新课讲解
新课讲解
知识点2 几何概率的计算及应用
合作探究
问题一 在转盘游戏中,当指针停止时,为什么指针指向红色区域的可能性大?
因为红色区域的面积大,所以指针落在红色的区域可能性大.
在有些问题中,实验的结果可能要用线段或平面(空间)区域表示,事件的概率定义为部分线段的长度或部分区域的面积(体积)和整条线段的长度或整个区域的面积(体积)的比.
结论
新课讲解
新课讲解
例
典例分析
2 某商厦开展“幸运一刻钟”有奖促销活动,办法如下:在营业时间9:00~21:00内随机产生一个15min的时段(如10:36~10:51),该时段内在该商厦购物的顾客可得到与购物款等额的奖券.小明的妈妈在商厦购买了一双价格为80元的运动鞋,那么她中奖的概率是多少?
解:商场的营业时间是12h,计720min,那么它的时间长度为
720min,可用一条线段AB来表示.
720
A
B
设幸运奖的起始时刻为点C,终止时刻为点D,则线段CD的时间长度为15min.
0
720
A
B
C
D
因此,小明妈妈中奖的概率为
CD的长
AB的长
新课讲解
3 在正方形中有一内切圆,随机撒一把芝麻,假设每一粒芝麻落在正方形内的每一点的可能性都是相等的,计算落在圆中的芝麻数与落在正方形中的芝麻数之比,并以此估计圆周率的值.
解:随机撒一把芝麻,每粒芝麻落在正方形内任何一 点是等可能的, 落在每个区域的芝麻数与这个区域的面积近似成正比,假设正方形的边长为2a,则
落在圆中的芝麻数
落在正方形中的芝麻数
≈
圆的面积
正方形的面积
新课讲解
例
课堂小结
综合与实践
概率在遗传学中的应用
几何概率的计算与应用
线段的长度或区域的面(体)积
线段的总长度或区域的总面(体)积
当堂小练
1.一个家庭有两个孩子,两个都是女孩的概率是_____.
2.若三枚鸟卵全部成功孵化,则三只雏鸟中恰有两只雄鸟的概率是_____.
1
4
3
8
当堂小练
3.人的血型常可分为A型、B型、AB型和O型、IAIA和IAi表现为A型,IBIB和IBi表现为B型,IAIB表现为AB型,ii表现为O型.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的.例如下表为A(IAi)型父亲和B(IBi)型母亲生下的子女血型基因型表.
(1)求表中O型子女的概率;
(2)父母都是AB型,生下子女也是AB型的概率是多少?
(2)
IA IB
IA IAIA IAIB
IB IAIB IBIB
IAIB
IAIB
1
2
1
4
(1)
4.有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率_________.
当堂小练
解:
D
拓展与延伸
1.在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM小于AC的概率为_______.
A
B
C
解:在AB上截取AC'=AC,于是
P(AM<AC)=P(AM<AC').
P(AM<AC)
第二十六章 概率初步
26.2 等可能情形下的概率计算
第1课时 利用概率公式求概率
1.了解概率在遗传学中的应用. (重点)
2.掌握几何概率的计算和应用.(难点)
学习目标
新课导入
情境导入
读一读下列俗语:
龙生龙,凤生凤,老鼠生儿会打洞.
虎父无犬子.
桂实生桂,桐实生桐.
种瓜得瓜,种豆得豆.
种豆其苗必豆,种瓜其苗必瓜.
这些俗语反映了什么现象?
新课讲解
知识点1 概率在遗传学中的应用
双亲的遗传物质混合后,子代的性状介于双亲之间.
答:品红色(介于红色和蓝色之间)
答:不能
问题一 红墨水与蓝墨水混合后的颜色?
问题二 混合后能否再将这两种墨水分开?
问题三 那么遗传是这样吗?
合作探究
新课讲解
想一想:为什么用豌豆做实验材料容易成功?
豌豆花特点:自花传粉,闭花授粉
纯种
自然状态下,一般都是
具有易于区分的性状
豌豆
同种生物
同种性状
不同表现类型
相对性状
新课讲解
遗传学中把生物体所表现的形态结构、生理特征和行为方式等统称为性状.如:豌豆的花色、种子形状、子叶颜色、茎的高矮等都可以称之为性状.
新课讲解
(高茎)
(矮茎)
P(亲本)
F1 (子一代)
(高茎)
孟德尔一对相对性状的杂交实验
想一想:为什么子一代全是高茎呢 难道矮茎就这样消失了吗?还是它依然存在只是隐藏起来了?
杂交
新课讲解
787 : 277
P
F1
F2
≈3:1
显性性状
隐性性状
性状分离
子二代出现了性状分离现象.
杂交
新课讲解
高茎豌豆和矮茎豌豆杂交实验的分析图解
Aa
×
A
a
A
a
AA
Aa
Aa
aa
AA
×
aa
高茎
矮茎
P
配子
Aa
F1
A
a
配子
F2
高茎
高茎
高茎
矮茎
新课讲解
新课讲解
例
典例分析
1 白化病是一种隐性的性状,如果N是正常的基因,a是白化病基因,那么携带一对基因Na的个体的皮肤,头发和眼球的颜色是正常的,而携带一对基因aa的个体将患有白化病.
(1)设母亲和父亲都携带成对基因Na,求他们有正常孩子的概率;
P(有正常孩子)=
(2)设母亲和父亲分别携带一对基因NN和Na,求他们有
正常孩子的概率和孩子患白血病的概率;
NN
Na
N
a
NN
Na
NN
Na
N
N
正常
正常
正常
正常
P(有正常孩子)=
P(孩子患白血病)=
新课讲解
(3)设母亲和父亲分别携带一对基因aa和Na,求他们有正常
孩子的概率和孩子患白血病的概率.
aa
Na
N
a
Na
aa
Na
aa
a
a
正常
白血病
正常
白血病
P(有正常孩子)=
P(孩子患白血病)=
新课讲解
新课讲解
知识点2 几何概率的计算及应用
合作探究
问题一 在转盘游戏中,当指针停止时,为什么指针指向红色区域的可能性大?
因为红色区域的面积大,所以指针落在红色的区域可能性大.
在有些问题中,实验的结果可能要用线段或平面(空间)区域表示,事件的概率定义为部分线段的长度或部分区域的面积(体积)和整条线段的长度或整个区域的面积(体积)的比.
结论
新课讲解
新课讲解
例
典例分析
2 某商厦开展“幸运一刻钟”有奖促销活动,办法如下:在营业时间9:00~21:00内随机产生一个15min的时段(如10:36~10:51),该时段内在该商厦购物的顾客可得到与购物款等额的奖券.小明的妈妈在商厦购买了一双价格为80元的运动鞋,那么她中奖的概率是多少?
解:商场的营业时间是12h,计720min,那么它的时间长度为
720min,可用一条线段AB来表示.
720
A
B
设幸运奖的起始时刻为点C,终止时刻为点D,则线段CD的时间长度为15min.
0
720
A
B
C
D
因此,小明妈妈中奖的概率为
CD的长
AB的长
新课讲解
3 在正方形中有一内切圆,随机撒一把芝麻,假设每一粒芝麻落在正方形内的每一点的可能性都是相等的,计算落在圆中的芝麻数与落在正方形中的芝麻数之比,并以此估计圆周率的值.
解:随机撒一把芝麻,每粒芝麻落在正方形内任何一 点是等可能的, 落在每个区域的芝麻数与这个区域的面积近似成正比,假设正方形的边长为2a,则
落在圆中的芝麻数
落在正方形中的芝麻数
≈
圆的面积
正方形的面积
新课讲解
例
课堂小结
综合与实践
概率在遗传学中的应用
几何概率的计算与应用
线段的长度或区域的面(体)积
线段的总长度或区域的总面(体)积
当堂小练
1.一个家庭有两个孩子,两个都是女孩的概率是_____.
2.若三枚鸟卵全部成功孵化,则三只雏鸟中恰有两只雄鸟的概率是_____.
1
4
3
8
当堂小练
3.人的血型常可分为A型、B型、AB型和O型、IAIA和IAi表现为A型,IBIB和IBi表现为B型,IAIB表现为AB型,ii表现为O型.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的.例如下表为A(IAi)型父亲和B(IBi)型母亲生下的子女血型基因型表.
(1)求表中O型子女的概率;
(2)父母都是AB型,生下子女也是AB型的概率是多少?
(2)
IA IB
IA IAIA IAIB
IB IAIB IBIB
IAIB
IAIB
1
2
1
4
(1)
4.有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率_________.
当堂小练
解:
D
拓展与延伸
1.在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM小于AC的概率为_______.
A
B
C
解:在AB上截取AC'=AC,于是
P(AM<AC)=P(AM<AC').
P(AM<AC)
