2021-2022学年冀教版数学八年级上册13.1 命题与证明 同步练习卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版数学八年级上册13.1 命题与证明 同步练习卷 (word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 76.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 00:00:00 | ||
图片预览

文档简介
2021年冀教版数学八年级上册
13.1《命题与证明》同步练习卷
一、选择题
1.下列命题中,是真命题的是( )
A.若互补的两角相等,则这两个角都是直角
B.直线是平角
C.不相交的两条直线叫做平行线
D.和为180°的两个角叫做邻补角
2.下列语句中,不是命题的是( )
A.若两角之和为90°,则这两个角互补
B.同角的余角相等
C.作线段的垂直平分线
D.相等的角是对顶角
3.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
A.a=-2 B.a= C.a=1 D.a=
4.下列命题中,是假命题的为( )
A.邻补角的平分线互相垂直
B.平行于同一直线的两条直线互相平行
C.如果一个角的两边分别平行于另一个角的两边,则这两个角一定相等
D.平行线的一组内错角的平分线互相平行
5.下列语句中,不属于命题的个数是( )
①延长线段AB;
②自然数都是整数;
③两个锐角的和一定是直角;
④同角的余角相等.
A.1 B.2 C.3 D.4
6.如图,下列条件中,能证明AD∥BC的是( )
A.∠A=∠C B.∠B=∠D C.∠B=∠C D.∠C+∠D=180°
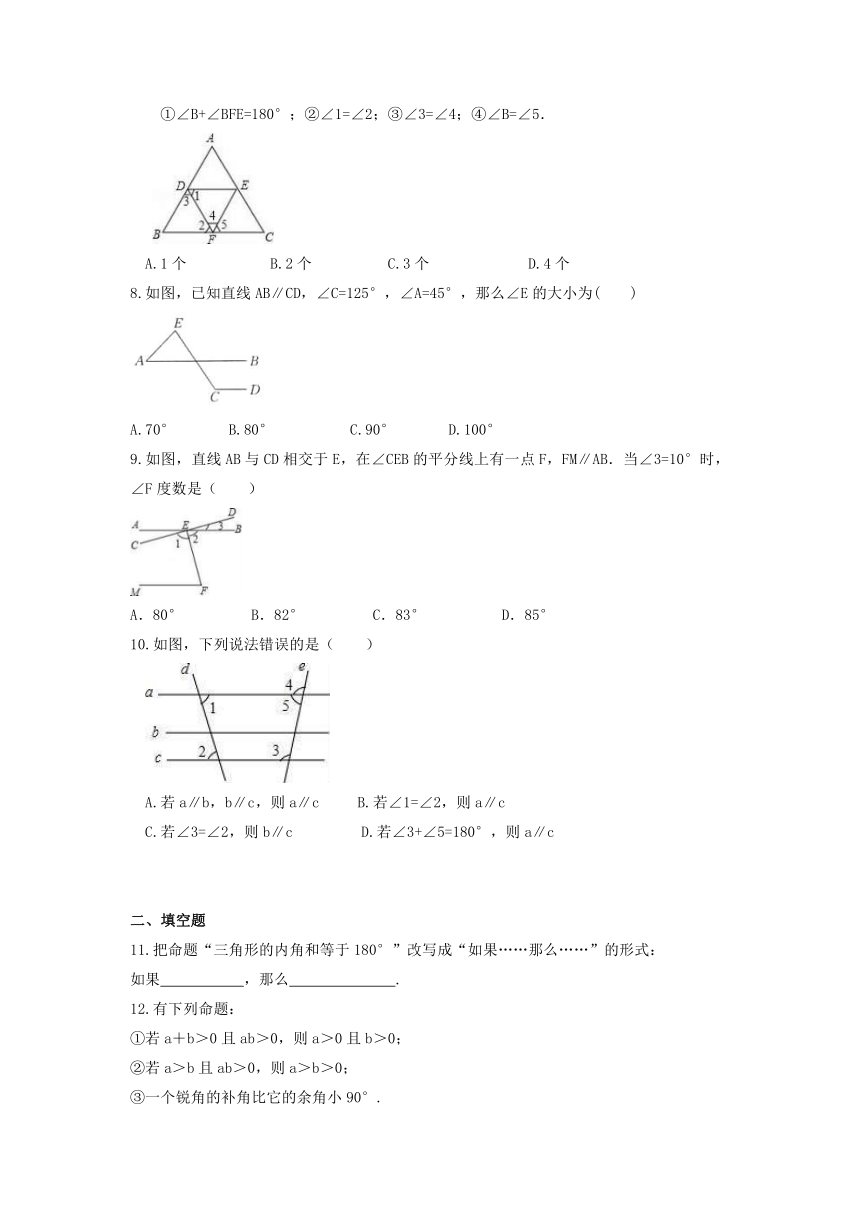
7.如图,下列能判定AB∥EF的条件有( )
①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
8.如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为( )
A.70° B.80° C.90° D.100°
9.如图,直线AB与CD相交于E,在∠CEB的平分线上有一点F,FM∥AB.当∠3=10°时,∠F度数是( )
A.80° B.82° C.83° D.85°
10.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
二、填空题
11.把命题“三角形的内角和等于180°”改写成“如果……那么……”的形式:
如果 ,那么 .
12.有下列命题:
①若a+b>0且ab>0,则a>0且b>0;
②若a>b且ab>0,则a>b>0;
③一个锐角的补角比它的余角小90°.
其中属于真命题的是____(填序号).
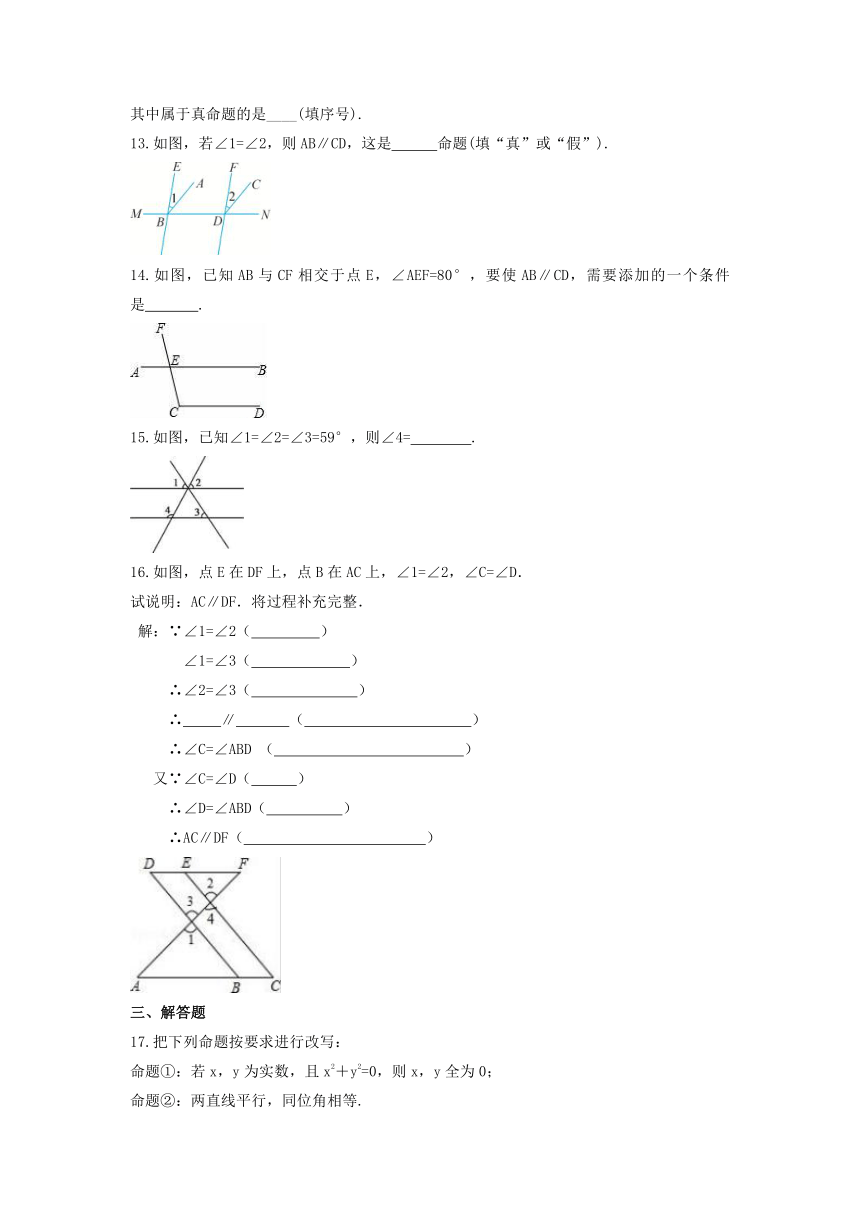
13.如图,若∠1=∠2,则AB∥CD,这是 命题(填“真”或“假”).
14.如图,已知AB与CF相交于点E,∠AEF=80°,要使AB∥CD,需要添加的一个条件是 .
15.如图,已知∠1=∠2=∠3=59°,则∠4= .
16.如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2( )
∠1=∠3( )
∴∠2=∠3( )
∴ ∥ ( )
∴∠C=∠ABD ( )
又∵∠C=∠D( )
∴∠D=∠ABD( )
∴AC∥DF( )
三、解答题
17.把下列命题按要求进行改写:
命题①:若x,y为实数,且x2+y2=0,则x,y全为0;
命题②:两直线平行,同位角相等.
(1)交换命题的条件和结论;
(2)同时否定命题的条件和结论;
(3)交换命题的条件和结论后,再同时否定新命题的条件和结论.
18.请你写出下列命题的逆命题.并判断真假性,若是假命题,请举出一个反例.
(1)如果a能被4整除,那么a一定是偶数;
(2)若|a|=|b|,则a=b.
19如图,∠1与∠D互余,∠C与∠D互余.求证:AB∥CD.
20.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=130°,∠FEC=15°.求∠ACF的度数.
参考答案
1.答案为:A.
2.答案为:C.
3.答案为:A.
4.答案为:C.
5.答案为:A.
6.答案为:D.
7.答案为:C
8.答案为:B.
9.答案为:D.
10.答案为:C.
11.答案为:如果三个角是三角形的内角,那么它们的和等于180°.
12.答案为:①.
13.答案为:假.
14.答案为:∠C=100°.
15.答案为:121°
16.答案为:∵∠1=∠2( 已知),
∠1=∠3( 对顶角相等),
∴∠2=∠3( 等量代换),
∴BD∥CE( 同位角相等,两直线平行),
∴∠C=∠ABD ( 两直线平行,同位角相等),
又∵∠C=∠D( 已知),
∴∠D=∠ABD( 等量代换),
∴AC∥DF( 内错角相等,两直线平行),
17.解:命题①:(1)若x,y为实数,且x,y全为0,则x2+y2=0;
(2)若x,y为实数,且x2+y2≠0,则x,y不全为0;
(3)若x,y为实数,且x,y不全为0,则x2+y2≠0.
命题②:(1)同位角相等,两直线平行;
(2)两直线不平行,同位角不相等;
(3)同位角不相等,两直线不平行.
18.解:(1)如果a是偶数,那么a能被4整除.假命题.
反例:如a=2是偶数,但2不能被4整除.
(2)若a=b,则|a|=|b|.真命题.
19.证明:∵∠1与∠D互余,∠C与∠D互余(已知),
∴∠1=∠C(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
20.解:∵AD∥BC,
∴∠ACB+∠DAC=180°.
又∵∠DAC=130°,
∴∠ACB=50°.
∵EF∥AD,AD∥BC,
∴EF∥BC.
∴∠BCE=∠FEC=15°.
又∵CE平分∠BCF,
∴∠BCF=2∠BCE=30°.
∴∠ACF=∠ACB-∠BCF=20°.
13.1《命题与证明》同步练习卷
一、选择题
1.下列命题中,是真命题的是( )
A.若互补的两角相等,则这两个角都是直角
B.直线是平角
C.不相交的两条直线叫做平行线
D.和为180°的两个角叫做邻补角
2.下列语句中,不是命题的是( )
A.若两角之和为90°,则这两个角互补
B.同角的余角相等
C.作线段的垂直平分线
D.相等的角是对顶角
3.能说明命题“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
A.a=-2 B.a= C.a=1 D.a=
4.下列命题中,是假命题的为( )
A.邻补角的平分线互相垂直
B.平行于同一直线的两条直线互相平行
C.如果一个角的两边分别平行于另一个角的两边,则这两个角一定相等
D.平行线的一组内错角的平分线互相平行
5.下列语句中,不属于命题的个数是( )
①延长线段AB;
②自然数都是整数;
③两个锐角的和一定是直角;
④同角的余角相等.
A.1 B.2 C.3 D.4
6.如图,下列条件中,能证明AD∥BC的是( )
A.∠A=∠C B.∠B=∠D C.∠B=∠C D.∠C+∠D=180°
7.如图,下列能判定AB∥EF的条件有( )
①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A.1个 B.2个 C.3个 D.4个
8.如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为( )
A.70° B.80° C.90° D.100°
9.如图,直线AB与CD相交于E,在∠CEB的平分线上有一点F,FM∥AB.当∠3=10°时,∠F度数是( )
A.80° B.82° C.83° D.85°
10.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
二、填空题
11.把命题“三角形的内角和等于180°”改写成“如果……那么……”的形式:
如果 ,那么 .
12.有下列命题:
①若a+b>0且ab>0,则a>0且b>0;
②若a>b且ab>0,则a>b>0;
③一个锐角的补角比它的余角小90°.
其中属于真命题的是____(填序号).
13.如图,若∠1=∠2,则AB∥CD,这是 命题(填“真”或“假”).
14.如图,已知AB与CF相交于点E,∠AEF=80°,要使AB∥CD,需要添加的一个条件是 .
15.如图,已知∠1=∠2=∠3=59°,则∠4= .
16.如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2( )
∠1=∠3( )
∴∠2=∠3( )
∴ ∥ ( )
∴∠C=∠ABD ( )
又∵∠C=∠D( )
∴∠D=∠ABD( )
∴AC∥DF( )
三、解答题
17.把下列命题按要求进行改写:
命题①:若x,y为实数,且x2+y2=0,则x,y全为0;
命题②:两直线平行,同位角相等.
(1)交换命题的条件和结论;
(2)同时否定命题的条件和结论;
(3)交换命题的条件和结论后,再同时否定新命题的条件和结论.
18.请你写出下列命题的逆命题.并判断真假性,若是假命题,请举出一个反例.
(1)如果a能被4整除,那么a一定是偶数;
(2)若|a|=|b|,则a=b.
19如图,∠1与∠D互余,∠C与∠D互余.求证:AB∥CD.
20.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=130°,∠FEC=15°.求∠ACF的度数.
参考答案
1.答案为:A.
2.答案为:C.
3.答案为:A.
4.答案为:C.
5.答案为:A.
6.答案为:D.
7.答案为:C
8.答案为:B.
9.答案为:D.
10.答案为:C.
11.答案为:如果三个角是三角形的内角,那么它们的和等于180°.
12.答案为:①.
13.答案为:假.
14.答案为:∠C=100°.
15.答案为:121°
16.答案为:∵∠1=∠2( 已知),
∠1=∠3( 对顶角相等),
∴∠2=∠3( 等量代换),
∴BD∥CE( 同位角相等,两直线平行),
∴∠C=∠ABD ( 两直线平行,同位角相等),
又∵∠C=∠D( 已知),
∴∠D=∠ABD( 等量代换),
∴AC∥DF( 内错角相等,两直线平行),
17.解:命题①:(1)若x,y为实数,且x,y全为0,则x2+y2=0;
(2)若x,y为实数,且x2+y2≠0,则x,y不全为0;
(3)若x,y为实数,且x,y不全为0,则x2+y2≠0.
命题②:(1)同位角相等,两直线平行;
(2)两直线不平行,同位角不相等;
(3)同位角不相等,两直线不平行.
18.解:(1)如果a是偶数,那么a能被4整除.假命题.
反例:如a=2是偶数,但2不能被4整除.
(2)若a=b,则|a|=|b|.真命题.
19.证明:∵∠1与∠D互余,∠C与∠D互余(已知),
∴∠1=∠C(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
20.解:∵AD∥BC,
∴∠ACB+∠DAC=180°.
又∵∠DAC=130°,
∴∠ACB=50°.
∵EF∥AD,AD∥BC,
∴EF∥BC.
∴∠BCE=∠FEC=15°.
又∵CE平分∠BCF,
∴∠BCF=2∠BCE=30°.
∴∠ACF=∠ACB-∠BCF=20°.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
