2021-2022学年华东师大版九年级数学下册 27.1.2圆的对称性同步练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册 27.1.2圆的对称性同步练习 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 165.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 13:09:16 | ||
图片预览


文档简介
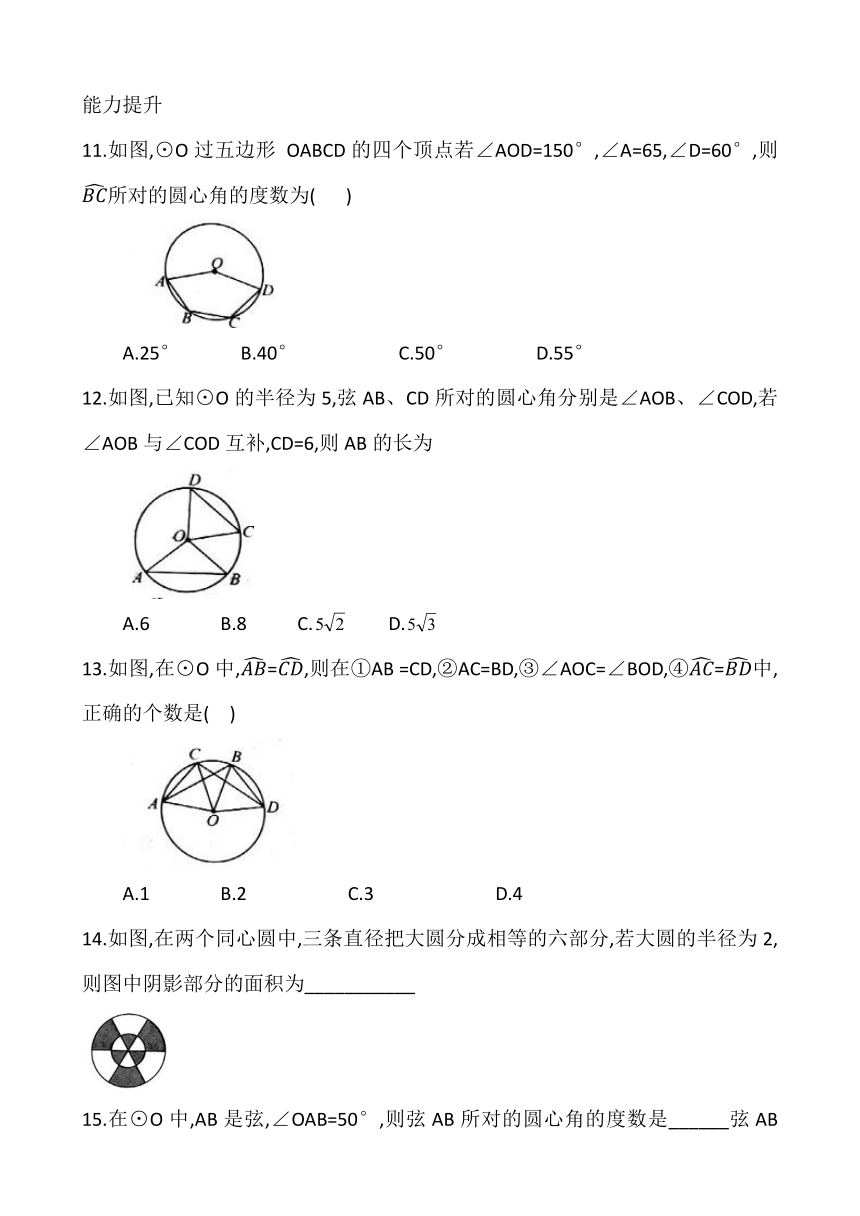
华师大版九年级数学27.1.2圆的对称性
第一课时 圆心角、弧、弦之间的关系同步练习 含答案
知识点1圆的对称性
1.下列说法中正确的有( )
①圆是轴对称图形;②圆是旋转对称图形;③圆不是中心对称图形;④圆的每一条直径都是它的对称轴;⑤圆的对称轴有无数条, 对称中心只有一个
A.1个 B.2个 C.3个 D.4个
2.下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
知识点2圆心角、弧、弦之间的关系
3.下列命题是真命题的是( )
A.相等的弦所对的弧相等
B.圆心角相等,其所对的弦相等
C.在同圆或等圆中,圆心角不等,所对的弦不相等
D.弦相等,则所对的圆心角相等
4.如图,两个同心圆的圆心为点O,A、B是大圆上的两点,OA交小圆于点A′,OB交小圆于点B′,连结A'B′、AB,那么( )
A OA=A'A B AB=A'B′
C.与所对圆心角的度数相等 D.的长度等于的长度
5.如图,在⊙O中,=,∠AOC=90°,则∠BOD的度数为( )
A.20 B.90° C.50 D.60°
6.如图,在⊙O中,C是的中点,∠A=60°,则∠BOC为___________
7.如图,AB为半圆O的直径,C、D、E为半圆弧上的点,==,∠BOE=5°,则∠AOC的度数为_____度
8.在同圆中劣弧AB的长是劣弧CD的两倍,那么弦AB________2CD.(填“>”“<”或“=”)
9.如图,在⊙O中,=,∠ACB=60°求证:∠AOB=∠BOC=∠AOC
10.如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E.求证:AD=BE
能力提升
11.如图,⊙O过五边形 OABCD的四个顶点若∠AOD=150°,∠A=65,∠D=60°,则所对的圆心角的度数为( )
A.25° B.40° C.50° D.55°
12.如图,已知⊙O的半径为5,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,CD=6,则AB的长为
A.6 B.8 C. D.
13.如图,在⊙O中,=,则在①AB =CD,②AC=BD,③∠AOC=∠BOD,④=中,正确的个数是( )
A.1 B.2 C.3 D.4
14.如图,在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆的半径为2,则图中阴影部分的面积为___________
15.在⊙O中,AB是弦,∠OAB=50°,则弦AB所对的圆心角的度数是______弦AB所对的弧的度数为___________
16.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为的中点,P是直径MN上一动点,则PA+PB的最小值为______
17.如图,已知直径BA与弦DC的延长线交于 点P,且PC=CO,=+,求∠DOB的度数.
18.如图,以 ABCD的顶点A为圆心、AB为半径作圆,分别交AD、BC于点E、F,延长BA交⊙A于点G.求证:=
拓展创新
19.如图,M、N是⊙O的弦AB的三等分点,过点M、N分别作AB的垂线,交于点C、D,那么==
答案
1.C
2.A
3.C
4.C
5.B
6.30°
7.15
8.<
9.证明:∵=,∴AB=AC.∴△ABC是等腰三角形又∵∠ACB=60°,∴△ABC是等边三角形.∴AB=BC=CA∴∠AOB=∠BOC=∠AOC
10.证明:连结OC.∵=,∴∠AOC=∠BOC.∵CD⊥OA,CE⊥OB,∴∠CDO=∠CEO=90°又∵CO=CO,∠DOC=∠EOC,∴△COD≌△COE.∴OD=OE.又∵AO=BO,∴AD=BE
11.B
12.B
13.D
14.2π
15.80°80°或280°
16.
17.∠DOB=∠P+∠D=67.5°
18.证明:连结AF.∵AB=AF,∴∠B=∠AFB.∵四边形ABCD是平行四边形,∴AD∥BC.∴:∠DAF=∠AFB,∠GAE=∠B∴∠GAE=∠DAF.∴=
19.解:≠≠.
第一课时 圆心角、弧、弦之间的关系同步练习 含答案
知识点1圆的对称性
1.下列说法中正确的有( )
①圆是轴对称图形;②圆是旋转对称图形;③圆不是中心对称图形;④圆的每一条直径都是它的对称轴;⑤圆的对称轴有无数条, 对称中心只有一个
A.1个 B.2个 C.3个 D.4个
2.下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
知识点2圆心角、弧、弦之间的关系
3.下列命题是真命题的是( )
A.相等的弦所对的弧相等
B.圆心角相等,其所对的弦相等
C.在同圆或等圆中,圆心角不等,所对的弦不相等
D.弦相等,则所对的圆心角相等
4.如图,两个同心圆的圆心为点O,A、B是大圆上的两点,OA交小圆于点A′,OB交小圆于点B′,连结A'B′、AB,那么( )
A OA=A'A B AB=A'B′
C.与所对圆心角的度数相等 D.的长度等于的长度
5.如图,在⊙O中,=,∠AOC=90°,则∠BOD的度数为( )
A.20 B.90° C.50 D.60°
6.如图,在⊙O中,C是的中点,∠A=60°,则∠BOC为___________
7.如图,AB为半圆O的直径,C、D、E为半圆弧上的点,==,∠BOE=5°,则∠AOC的度数为_____度
8.在同圆中劣弧AB的长是劣弧CD的两倍,那么弦AB________2CD.(填“>”“<”或“=”)
9.如图,在⊙O中,=,∠ACB=60°求证:∠AOB=∠BOC=∠AOC
10.如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E.求证:AD=BE
能力提升
11.如图,⊙O过五边形 OABCD的四个顶点若∠AOD=150°,∠A=65,∠D=60°,则所对的圆心角的度数为( )
A.25° B.40° C.50° D.55°
12.如图,已知⊙O的半径为5,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,CD=6,则AB的长为
A.6 B.8 C. D.
13.如图,在⊙O中,=,则在①AB =CD,②AC=BD,③∠AOC=∠BOD,④=中,正确的个数是( )
A.1 B.2 C.3 D.4
14.如图,在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆的半径为2,则图中阴影部分的面积为___________
15.在⊙O中,AB是弦,∠OAB=50°,则弦AB所对的圆心角的度数是______弦AB所对的弧的度数为___________
16.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为的中点,P是直径MN上一动点,则PA+PB的最小值为______
17.如图,已知直径BA与弦DC的延长线交于 点P,且PC=CO,=+,求∠DOB的度数.
18.如图,以 ABCD的顶点A为圆心、AB为半径作圆,分别交AD、BC于点E、F,延长BA交⊙A于点G.求证:=
拓展创新
19.如图,M、N是⊙O的弦AB的三等分点,过点M、N分别作AB的垂线,交于点C、D,那么==
答案
1.C
2.A
3.C
4.C
5.B
6.30°
7.15
8.<
9.证明:∵=,∴AB=AC.∴△ABC是等腰三角形又∵∠ACB=60°,∴△ABC是等边三角形.∴AB=BC=CA∴∠AOB=∠BOC=∠AOC
10.证明:连结OC.∵=,∴∠AOC=∠BOC.∵CD⊥OA,CE⊥OB,∴∠CDO=∠CEO=90°又∵CO=CO,∠DOC=∠EOC,∴△COD≌△COE.∴OD=OE.又∵AO=BO,∴AD=BE
11.B
12.B
13.D
14.2π
15.80°80°或280°
16.
17.∠DOB=∠P+∠D=67.5°
18.证明:连结AF.∵AB=AF,∴∠B=∠AFB.∵四边形ABCD是平行四边形,∴AD∥BC.∴:∠DAF=∠AFB,∠GAE=∠B∴∠GAE=∠DAF.∴=
19.解:≠≠.
