2021-2022学年华东师大版九年级数学下册27.2.3 切线 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册27.2.3 切线 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 162.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 13:06:56 | ||
图片预览

文档简介
华师大版九年级数学27.2.3切线
第1课时 切线的判定与性质同步练习 含答案
知识点1切线的判定
1.下列说法中,不正确的是( )
A.与圆只有一个交点的直线是圆的切线
B.经过半径的外端,且垂直于这条半径的直线是圆的切线
C.与圆心的距离等于这个圆的半径的直线是圆的切线
D.垂直于半径的直线是圆的切线
2.如图,AB是⊙0O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是 ( )
A .CD=DB B. AB=AC C. DE= DO D.AC∥OD
3.如图,P是∠AOB的平分线OC上一点,PEOA于点E,以点P为圆心,PE长为半径作⊙P.求证:⊙P与OB相切
4.(1)如图①,△ABC内接于⊙O,AB为直径∠CAE=∠B,试说明AE与⊙O相切于点A.
(2)在图②中,若AB为非直径的弦,∠CAE=∠B,AE还与⊙O相切于点A吗 请说明理由
知识点2切线的性质
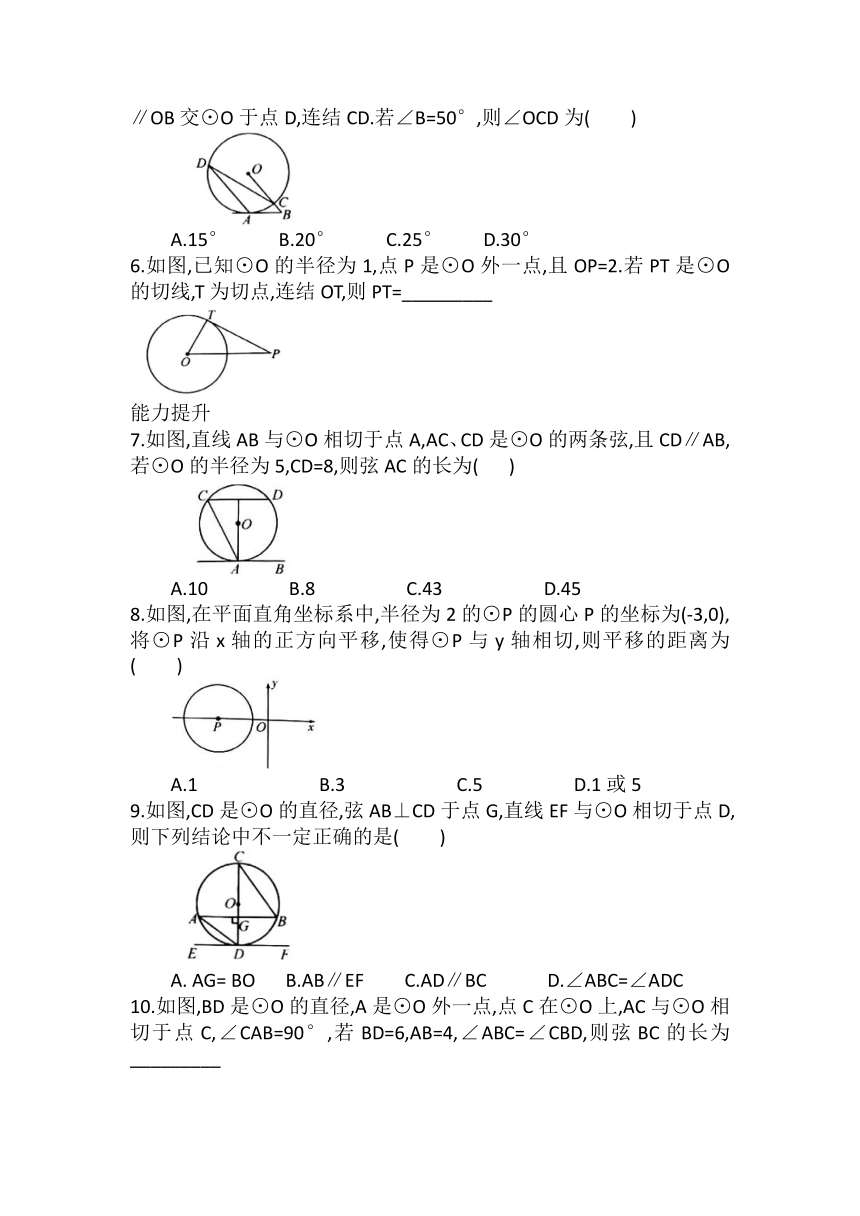
5.如图,在⊙O中,AB切⊙O于点A,连结OB交⊙O于点C,过点A作AD∥OB交⊙O于点D,连结CD.若∠B=50°,则∠OCD为( )
A.15° B.20° C.25° D.30°
6.如图,已知⊙O的半径为1,点P是⊙O外一点,且OP=2.若PT是⊙O的切线,T为切点,连结OT,则PT=_________
能力提升
7.如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为5,CD=8,则弦AC的长为( )
A.10 B.8 C.43 D.45
8.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴的正方向平移,使得⊙P与y轴相切,则平移的距离为( )
A.1 B.3 C.5 D.1或5
9.如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )
A. AG= BO B.AB∥EF C.AD∥BC D.∠ABC=∠ADC
10.如图,BD是⊙O的直径,A是⊙O外一点,点C在⊙O上,AC与⊙O相切于点C,∠CAB=90°,若BD=6,AB=4,∠ABC=∠CBD,则弦BC的长为_________
11.如图,AB是⊙O的直径,AC是⊙O的弦,OD⊥AC于点D,连结OC,过点D作DF∥OC交AB于点F,过点B的切线交AC的延长线于点E 若AD=4,DF=,则BE=___
12.如图,在Rt△AOB中,∠AOB=90°,以点O为圆心,OA为半径的圆交AB于点C,点D在边OB上,且CD=BD
(1)判断直线CD与⊙O的位置关系,并说明理由
(2)已知tan∠ODC=,AB=A0,求⊙O的半径.
13.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D,E为BC边的中点,连结DE
(1)求证:DE是⊙O的切线
(2)填空
①若∠B=30°,AC=,则DE=__________
②当∠B=_______ 时,以O、D、E、C为顶点的四边形是正方形
拓展创新
14.如图,已知AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F连结OC、AC
(1)求证:AC平分∠DAO
(2)若∠DAO=105°,∠E=30°,①∠OCE的度数为 ;
②若⊙O的半径为,求线段EF的长
答案
1.D
2.C
3.证明:过点P作PD⊥OB于点D,∵P是∠AOB的平分线OC上一点,PE⊥OA,PD⊥OB,∴PD=PE,即点P到射线OB的距离等于⊙P的半径PE∴⊙P与OB相切
4.解:(1)OA⊥AE.AE与⊙O相切于点A
(2)∴OA⊥AE.∴AE还与⊙O相切于点A
5.B
6.
7.D
8.D
9.C
10.
11.
12.解:(1)直线CD与⊙O相切.理由如下:连结OC
∵OA=OC,CD=BD,∴∠A=∠ACO,∠B=∠DCB.∵∠AOB=90°,∴∠A+∠B=90.∴∠ACO+∠DCB=9∴∠OCD=90°.∴OC⊥CD.又∵OC为⊙O的半径,∴直线CD与⊙O相切
(2)⊙O的半径为24
13.(1)证明:连结OD.∵AC是⊙O的直径,∴∠ADC=90∴∠CDB=90°.又∵E为BC边的中点,∴DE=CE=BC∴∠DCE=∠CDE.∵OC=OD,∴∠OCD=∠ODC.∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°∴∠ODE=90°,即OD⊥DE.∴DE是⊙O的切线.
(2)①3 ②45
14.(1)证明:∵CD是⊙O的切线,∴OC⊥CD.又∵AD⊥CD,∴AD∥OC.∴∠DAC=∠OCA.∵OC=OA,∴∠OCA=∠OAC.∴∠OAC=∠DAC.∴AC平分∠DAO
(2)①45
②EF=2-2
第1课时 切线的判定与性质同步练习 含答案
知识点1切线的判定
1.下列说法中,不正确的是( )
A.与圆只有一个交点的直线是圆的切线
B.经过半径的外端,且垂直于这条半径的直线是圆的切线
C.与圆心的距离等于这个圆的半径的直线是圆的切线
D.垂直于半径的直线是圆的切线
2.如图,AB是⊙0O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是 ( )
A .CD=DB B. AB=AC C. DE= DO D.AC∥OD
3.如图,P是∠AOB的平分线OC上一点,PEOA于点E,以点P为圆心,PE长为半径作⊙P.求证:⊙P与OB相切
4.(1)如图①,△ABC内接于⊙O,AB为直径∠CAE=∠B,试说明AE与⊙O相切于点A.
(2)在图②中,若AB为非直径的弦,∠CAE=∠B,AE还与⊙O相切于点A吗 请说明理由
知识点2切线的性质
5.如图,在⊙O中,AB切⊙O于点A,连结OB交⊙O于点C,过点A作AD∥OB交⊙O于点D,连结CD.若∠B=50°,则∠OCD为( )
A.15° B.20° C.25° D.30°
6.如图,已知⊙O的半径为1,点P是⊙O外一点,且OP=2.若PT是⊙O的切线,T为切点,连结OT,则PT=_________
能力提升
7.如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为5,CD=8,则弦AC的长为( )
A.10 B.8 C.43 D.45
8.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴的正方向平移,使得⊙P与y轴相切,则平移的距离为( )
A.1 B.3 C.5 D.1或5
9.如图,CD是⊙O的直径,弦AB⊥CD于点G,直线EF与⊙O相切于点D,则下列结论中不一定正确的是( )
A. AG= BO B.AB∥EF C.AD∥BC D.∠ABC=∠ADC
10.如图,BD是⊙O的直径,A是⊙O外一点,点C在⊙O上,AC与⊙O相切于点C,∠CAB=90°,若BD=6,AB=4,∠ABC=∠CBD,则弦BC的长为_________
11.如图,AB是⊙O的直径,AC是⊙O的弦,OD⊥AC于点D,连结OC,过点D作DF∥OC交AB于点F,过点B的切线交AC的延长线于点E 若AD=4,DF=,则BE=___
12.如图,在Rt△AOB中,∠AOB=90°,以点O为圆心,OA为半径的圆交AB于点C,点D在边OB上,且CD=BD
(1)判断直线CD与⊙O的位置关系,并说明理由
(2)已知tan∠ODC=,AB=A0,求⊙O的半径.
13.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D,E为BC边的中点,连结DE
(1)求证:DE是⊙O的切线
(2)填空
①若∠B=30°,AC=,则DE=__________
②当∠B=_______ 时,以O、D、E、C为顶点的四边形是正方形
拓展创新
14.如图,已知AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F连结OC、AC
(1)求证:AC平分∠DAO
(2)若∠DAO=105°,∠E=30°,①∠OCE的度数为 ;
②若⊙O的半径为,求线段EF的长
答案
1.D
2.C
3.证明:过点P作PD⊥OB于点D,∵P是∠AOB的平分线OC上一点,PE⊥OA,PD⊥OB,∴PD=PE,即点P到射线OB的距离等于⊙P的半径PE∴⊙P与OB相切
4.解:(1)OA⊥AE.AE与⊙O相切于点A
(2)∴OA⊥AE.∴AE还与⊙O相切于点A
5.B
6.
7.D
8.D
9.C
10.
11.
12.解:(1)直线CD与⊙O相切.理由如下:连结OC
∵OA=OC,CD=BD,∴∠A=∠ACO,∠B=∠DCB.∵∠AOB=90°,∴∠A+∠B=90.∴∠ACO+∠DCB=9∴∠OCD=90°.∴OC⊥CD.又∵OC为⊙O的半径,∴直线CD与⊙O相切
(2)⊙O的半径为24
13.(1)证明:连结OD.∵AC是⊙O的直径,∴∠ADC=90∴∠CDB=90°.又∵E为BC边的中点,∴DE=CE=BC∴∠DCE=∠CDE.∵OC=OD,∴∠OCD=∠ODC.∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°∴∠ODE=90°,即OD⊥DE.∴DE是⊙O的切线.
(2)①3 ②45
14.(1)证明:∵CD是⊙O的切线,∴OC⊥CD.又∵AD⊥CD,∴AD∥OC.∴∠DAC=∠OCA.∵OC=OA,∴∠OCA=∠OAC.∴∠OAC=∠DAC.∴AC平分∠DAO
(2)①45
②EF=2-2
