2021-2022学年华东师大版九年级数学下册 27.3圆中的计算问题 第1课时 弧长和扇形的面积 同步练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册 27.3圆中的计算问题 第1课时 弧长和扇形的面积 同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 187.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-02 13:37:58 | ||
图片预览


文档简介
华师大版九年级数学27.3圆中的计算问题
第1课时 弧长和扇形的面积 同步练习 含答案
知识点1弧长的计算
1.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A`OB′,则点A运动的路径的长为 ( )
A.π B.2π C.4π D.8π
2.如图,等边三角形ABC的三个顶点都在⊙O上,AD是⊙O的直径.若OA=3,则劣弧BD的长是( )
A. B.π C. D.2π
3.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC为半径画弧,交AB于点D,则扇形CAD的周长是(结果保留π)
A.1+π B.2+ C.1+ D.2+
4.若扇形的圆心角为30°,半径为17,则扇形的弧长为________
5.如图,在□ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为_________
6.如图,在扇形OAB中∠AOB=110°,半径OA=6,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则阴影部分的周长为_____
知识点2扇形面积的计算
7.如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
8.扇形的半径为3cm,弧长为2πcm,则该扇形的面积为___________
9.如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2,则图中阴影部分的面积是_______
10.如图,在△ABC中,O为BC边上的一点,以O为圆心的半圆分别与AB、AC相切于点M、N.已知∠BAC=120°,AB+AC=16,的长为π,求图中阴影部分的面积
能力提升
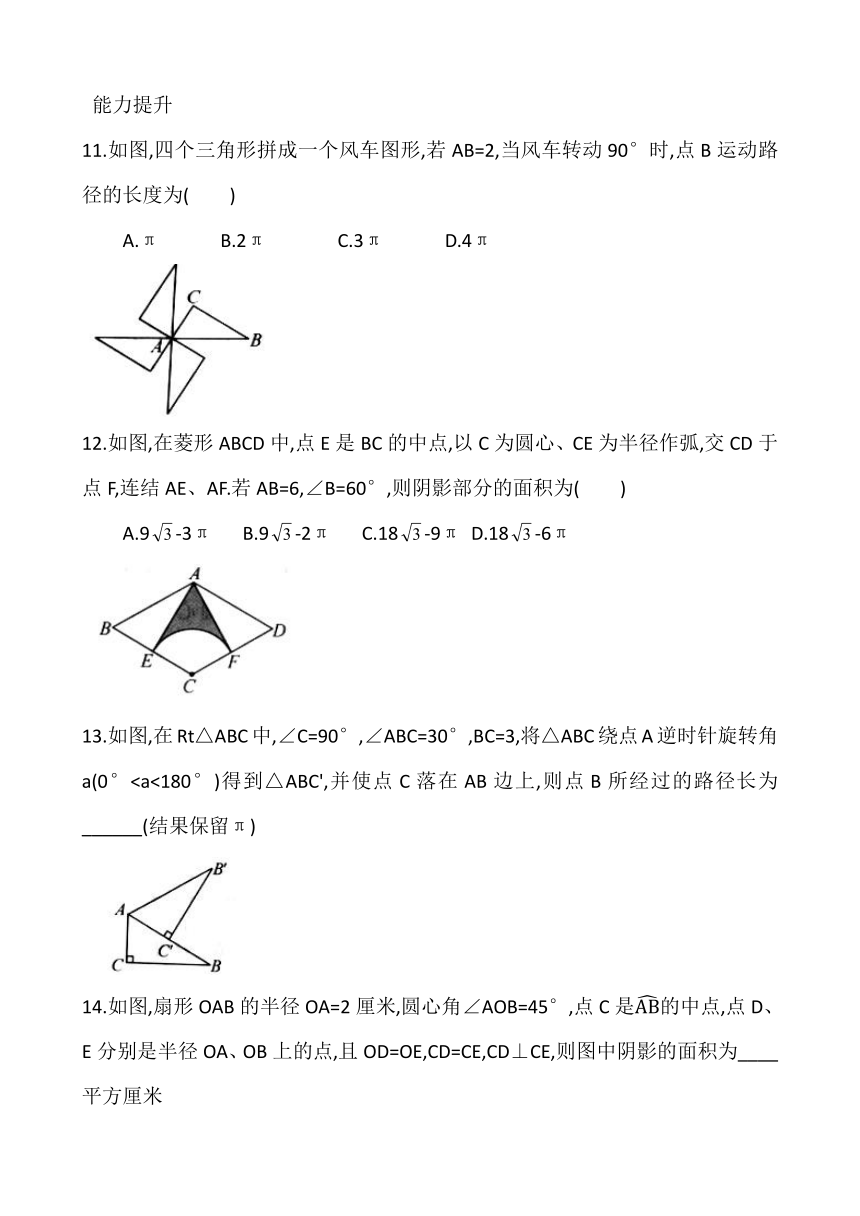
11.如图,四个三角形拼成一个风车图形,若AB=2,当风车转动90°时,点B运动路径的长度为( )
A.π B.2π C.3π D.4π
12.如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连结AE、AF.若AB=6,∠B=60°,则阴影部分的面积为( )
A.9-3π B.9-2π C.18-9π D.18-6π
13.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BC=3,将△ABC绕点A逆时针旋转角a(0°14.如图,扇形OAB的半径OA=2厘米,圆心角∠AOB=45°,点C是的中点,点D、E分别是半径OA、OB上的点,且OD=OE,CD=CE,CD⊥CE,则图中阴影的面积为____平方厘米
15.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为_________
16.如图,六边形 ABCDEF是正六边形,曲线FA1B1C1D1E1F1…叫做“正六边形的渐开线”,FA1、A1B1、B1C1、C1D1 、D1E1、E1F1…的圆心依次按A、B、C、D、 E、F循环,且每段弧所对的圆心角均为正六边形的一个外角.当AB=1时,曲线FA1B1C1D1E1F1的长度是___________
17.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作果⊙O的切线,交OD的延长线于点E,连结 BE
(1)求证:BE是⊙O的切线
(2)设OE交⊙O于点F,若DF=2,BC=4,求线段EF的长
(3)在(2)的条件下,求阴影部分的面积
拓展创新
18.如图,将△ABC绕点B顺时针旋转60°得到△DBE,点C的对应点E恰好落在AB的延长线上,连结AD
(1)求证:BC∥AD
(2)若AB=4,BC=1,求A、C两点旋转所经过的路径长之和
答案
1.B
2.B
3.D
4.
5.π
6.2π+6
7.B
8.3π
9.
10.
12 A
13.π
14.
15.
16.7π
17.(1)证明:连结OC.∵OD⊥BC,∴CD=BD.∴OE为BC的垂直
∴EB=EC.∴∠EBC=∠ECB.∵OB=OC,∴∠OBC∠OCB.∴∠OBC+∠EBC=∠OCB+∠ECB,即∠OBE∠OCE.∵CE是⊙O的切线,∴OC⊥CE.∴∠OCE=90∴∠OBE=90°∴OB⊥BE.∴BE是⊙O的切线.
(2)4.
(3)
18.(1)证明:由题意,得△ABC≌△DBE,且∠ABD=∠CBE=60°∴AB=BD.∴△ABD是等边三角形.∴∠DAB=60∠CBE=∠DAB.∴BC∥AD
(2)解:
第1课时 弧长和扇形的面积 同步练习 含答案
知识点1弧长的计算
1.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A`OB′,则点A运动的路径的长为 ( )
A.π B.2π C.4π D.8π
2.如图,等边三角形ABC的三个顶点都在⊙O上,AD是⊙O的直径.若OA=3,则劣弧BD的长是( )
A. B.π C. D.2π
3.如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC为半径画弧,交AB于点D,则扇形CAD的周长是(结果保留π)
A.1+π B.2+ C.1+ D.2+
4.若扇形的圆心角为30°,半径为17,则扇形的弧长为________
5.如图,在□ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为_________
6.如图,在扇形OAB中∠AOB=110°,半径OA=6,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则阴影部分的周长为_____
知识点2扇形面积的计算
7.如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
8.扇形的半径为3cm,弧长为2πcm,则该扇形的面积为___________
9.如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2,则图中阴影部分的面积是_______
10.如图,在△ABC中,O为BC边上的一点,以O为圆心的半圆分别与AB、AC相切于点M、N.已知∠BAC=120°,AB+AC=16,的长为π,求图中阴影部分的面积
能力提升
11.如图,四个三角形拼成一个风车图形,若AB=2,当风车转动90°时,点B运动路径的长度为( )
A.π B.2π C.3π D.4π
12.如图,在菱形ABCD中,点E是BC的中点,以C为圆心、CE为半径作弧,交CD于点F,连结AE、AF.若AB=6,∠B=60°,则阴影部分的面积为( )
A.9-3π B.9-2π C.18-9π D.18-6π
13.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BC=3,将△ABC绕点A逆时针旋转角a(0°
15.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为_________
16.如图,六边形 ABCDEF是正六边形,曲线FA1B1C1D1E1F1…叫做“正六边形的渐开线”,FA1、A1B1、B1C1、C1D1 、D1E1、E1F1…的圆心依次按A、B、C、D、 E、F循环,且每段弧所对的圆心角均为正六边形的一个外角.当AB=1时,曲线FA1B1C1D1E1F1的长度是___________
17.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作果⊙O的切线,交OD的延长线于点E,连结 BE
(1)求证:BE是⊙O的切线
(2)设OE交⊙O于点F,若DF=2,BC=4,求线段EF的长
(3)在(2)的条件下,求阴影部分的面积
拓展创新
18.如图,将△ABC绕点B顺时针旋转60°得到△DBE,点C的对应点E恰好落在AB的延长线上,连结AD
(1)求证:BC∥AD
(2)若AB=4,BC=1,求A、C两点旋转所经过的路径长之和
答案
1.B
2.B
3.D
4.
5.π
6.2π+6
7.B
8.3π
9.
10.
12 A
13.π
14.
15.
16.7π
17.(1)证明:连结OC.∵OD⊥BC,∴CD=BD.∴OE为BC的垂直
∴EB=EC.∴∠EBC=∠ECB.∵OB=OC,∴∠OBC∠OCB.∴∠OBC+∠EBC=∠OCB+∠ECB,即∠OBE∠OCE.∵CE是⊙O的切线,∴OC⊥CE.∴∠OCE=90∴∠OBE=90°∴OB⊥BE.∴BE是⊙O的切线.
(2)4.
(3)
18.(1)证明:由题意,得△ABC≌△DBE,且∠ABD=∠CBE=60°∴AB=BD.∴△ABD是等边三角形.∴∠DAB=60∠CBE=∠DAB.∴BC∥AD
(2)解:
