3.9 弧长及扇形面积 课件(共20张PPT)
文档属性
| 名称 | 3.9 弧长及扇形面积 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 74.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览







文档简介
(共20张PPT)
北师版九年级下册 圆
§3.9 弧长及扇形面积
1.经历探索弧长计算公式和扇形面积计算公式的过程,培养学生的探索能力.
2.了解弧长计算公式和扇形面积计算公式,并运用公式解决问题;
3、能够 综合运用“弧长和扇形面积”的两种公式处理各类问题.
o
p
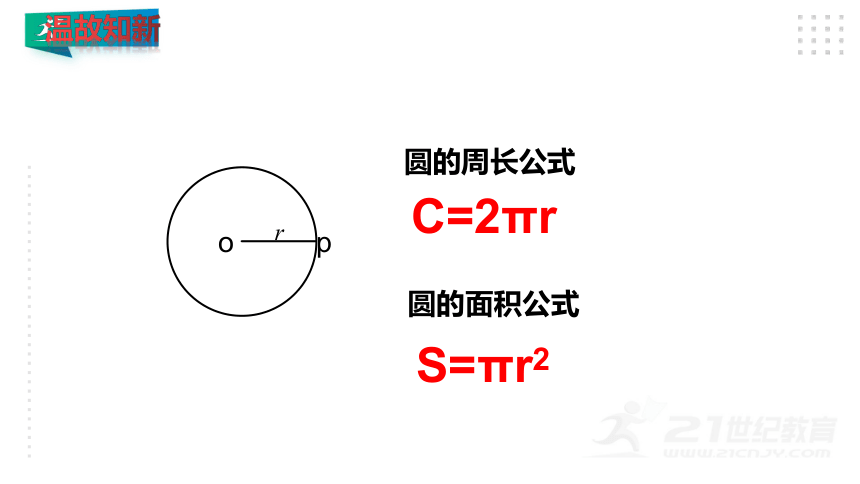
圆的周长公式
圆的面积公式
C=2πr
S=πr2
温故知新
如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
解:(1)转动一周时,∵C=2πr=20πcm。
(2)转动1°时,∵1°所对弧长是圆周长的 。
∴1°所对弧长=20π× = cm 。
(3)转动n°时,n°所对弧长是 cm 。
情境导入
1800
900
450
n0
圆心角占整个周角的
所对弧长是
新知探究
如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长的计算公式为:
【变式】已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度.
=
cm
答:此圆弧的长度为
cm
解:
弧长计算公式
归纳小结
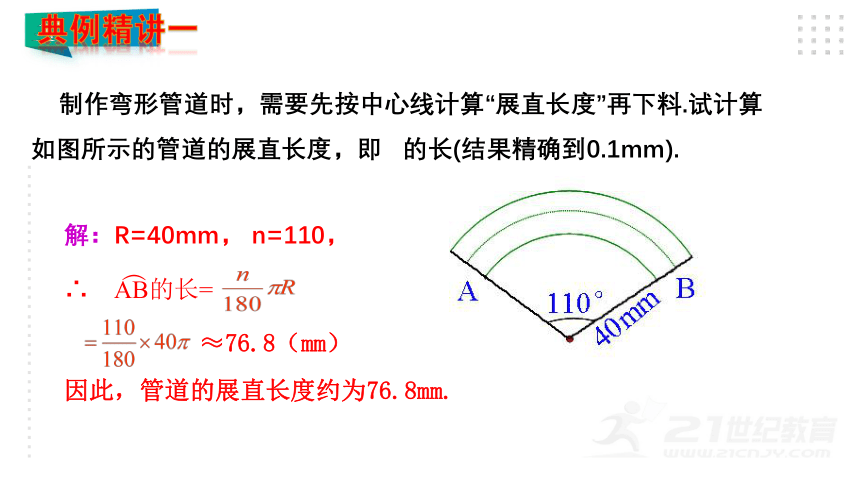
制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即 的长(结果精确到0.1mm).
解:R=40mm, n=110,
∴ AB的长=
︵
≈76.8(mm)
因此,管道的展直长度约为76.8mm.
典例精讲一
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m长的绳子,绳子一头拴着一只狗.
(1)如果这只狗只能绕着柱子转动120°的角,那么它的最大活动区域为多少
情境导入
解析:小狗只能在草地上活动,其活动区域的最大面积是以点O为圆心,3m长为半径,圆心角是120°的扇形面积,
圆心角为120°扇形面积占整个圆面积的
S= ×πr2= 3π m2
(2)如果这只狗只能绕着柱子转动n°的角,那么它的最大活动区域为多少
圆心角为n°扇形面积占整个圆面积的
S= ×πr2= m2
如图,由组成圆心角的两条半径
和圆心角所对的弧所围成的图形
叫扇形.
怎样计算圆心角是n0
的扇形面积?
扇形:
新知探究
1800
900
450
n0
圆心角占整个周角的
所对扇形面积是
新知探究
如果扇形面积为S,圆心角度数为n0,圆半径是r,那么 扇形面积
S计算公式为:
扇形面积计算公式
归纳小结
如图,圆心角为60°的扇形的半径为10厘米,求这个扇形的面积和周长.(π≈3.14)
≈52.33(平方厘米);
扇形的周长为
≈ 30.47(厘米).
解:因为n=60°,r=10厘米,所以扇形面积为
典例精讲二
已知扇形的圆心角为450,弧长等于 ,求:该扇形的面积。
解:∵n=45,l=
∴r=2
解法一:
解法二:
典例精讲三
跟踪练习
1.一个扇形的圆心角为90o,半径为2,则弧长=_____,扇形面积=_______.
2.一个扇形的弧长为20πcm,面积是240πcm2,则该扇形的圆心角为_______.
3.已知扇形的圆心角为120°,半径为6,则扇形的弧长是( )
A. 3π B.4π C.5π D.6π
π
π
150o
B
4.如图的五个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速
度从A点到B点,甲虫沿 路线爬行,乙虫沿
路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定
A
C
G
F
E
B
A3
A2
A1
D
C
跟踪练习
课堂练习
C
B
3.120°的圆心角所对的弧长是6π,则此弧所在圆的半径是( )
A.3 B.4
C.9 D.18
4. 如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了
108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A.π cm B.2π cm
C.3π cm D.5π cm
C
C
课堂练习
一、弧长的计算公式
二、扇形面积计算公式
课本P101页 随堂练习 1,2题
102页习题1,2,3,4题
课下作业
北师版九年级下册 圆
§3.9 弧长及扇形面积
1.经历探索弧长计算公式和扇形面积计算公式的过程,培养学生的探索能力.
2.了解弧长计算公式和扇形面积计算公式,并运用公式解决问题;
3、能够 综合运用“弧长和扇形面积”的两种公式处理各类问题.
o
p
圆的周长公式
圆的面积公式
C=2πr
S=πr2
温故知新
如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
解:(1)转动一周时,∵C=2πr=20πcm。
(2)转动1°时,∵1°所对弧长是圆周长的 。
∴1°所对弧长=20π× = cm 。
(3)转动n°时,n°所对弧长是 cm 。
情境导入
1800
900
450
n0
圆心角占整个周角的
所对弧长是
新知探究
如果弧长为l,圆心角度数为n,圆的半径为r,那么,弧长的计算公式为:
【变式】已知圆弧的半径为50厘米,圆心角为60°,求此圆弧的长度.
=
cm
答:此圆弧的长度为
cm
解:
弧长计算公式
归纳小结
制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即 的长(结果精确到0.1mm).
解:R=40mm, n=110,
∴ AB的长=
︵
≈76.8(mm)
因此,管道的展直长度约为76.8mm.
典例精讲一
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m长的绳子,绳子一头拴着一只狗.
(1)如果这只狗只能绕着柱子转动120°的角,那么它的最大活动区域为多少
情境导入
解析:小狗只能在草地上活动,其活动区域的最大面积是以点O为圆心,3m长为半径,圆心角是120°的扇形面积,
圆心角为120°扇形面积占整个圆面积的
S= ×πr2= 3π m2
(2)如果这只狗只能绕着柱子转动n°的角,那么它的最大活动区域为多少
圆心角为n°扇形面积占整个圆面积的
S= ×πr2= m2
如图,由组成圆心角的两条半径
和圆心角所对的弧所围成的图形
叫扇形.
怎样计算圆心角是n0
的扇形面积?
扇形:
新知探究
1800
900
450
n0
圆心角占整个周角的
所对扇形面积是
新知探究
如果扇形面积为S,圆心角度数为n0,圆半径是r,那么 扇形面积
S计算公式为:
扇形面积计算公式
归纳小结
如图,圆心角为60°的扇形的半径为10厘米,求这个扇形的面积和周长.(π≈3.14)
≈52.33(平方厘米);
扇形的周长为
≈ 30.47(厘米).
解:因为n=60°,r=10厘米,所以扇形面积为
典例精讲二
已知扇形的圆心角为450,弧长等于 ,求:该扇形的面积。
解:∵n=45,l=
∴r=2
解法一:
解法二:
典例精讲三
跟踪练习
1.一个扇形的圆心角为90o,半径为2,则弧长=_____,扇形面积=_______.
2.一个扇形的弧长为20πcm,面积是240πcm2,则该扇形的圆心角为_______.
3.已知扇形的圆心角为120°,半径为6,则扇形的弧长是( )
A. 3π B.4π C.5π D.6π
π
π
150o
B
4.如图的五个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速
度从A点到B点,甲虫沿 路线爬行,乙虫沿
路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定
A
C
G
F
E
B
A3
A2
A1
D
C
跟踪练习
课堂练习
C
B
3.120°的圆心角所对的弧长是6π,则此弧所在圆的半径是( )
A.3 B.4
C.9 D.18
4. 如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了
108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A.π cm B.2π cm
C.3π cm D.5π cm
C
C
课堂练习
一、弧长的计算公式
二、扇形面积计算公式
课本P101页 随堂练习 1,2题
102页习题1,2,3,4题
课下作业
