2021-2022学年度北师大版九年级数学上册课件 2.1认识一元二次方程(第1课时)(共12张ppt)
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学上册课件 2.1认识一元二次方程(第1课时)(共12张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 400.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 21:20:16 | ||
图片预览





文档简介
(共12张PPT)
(第一课时)
绿苑小区住宅设计,准备在每两幢
楼之间,开辟面积为900平方米的一块
长方形绿地,并且长比宽多10米,则绿
地的长和宽各为多少?
设宽为x,则长为(x+10)
整理可得
学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册,求这两年的平均增长率。
设这两年的平均增长率为x
今年底的图书数是5(1+x)万册
明年底的图书数是5(1+x)(1+x)万册
可列方程
只含有一个未知数,并且未知数的
最高次数是为2的整式方程叫做一元二
次方程。
(1)是整式方程;
(2)只含有一个未知数;
(3)未知数的最高次数是2。
一元一次方程:
一元二次方程:
二元一次方程:
含一个未知数,最高次数为1
含二个未知数,最高次数为1
含一个未知数,最高次数为2
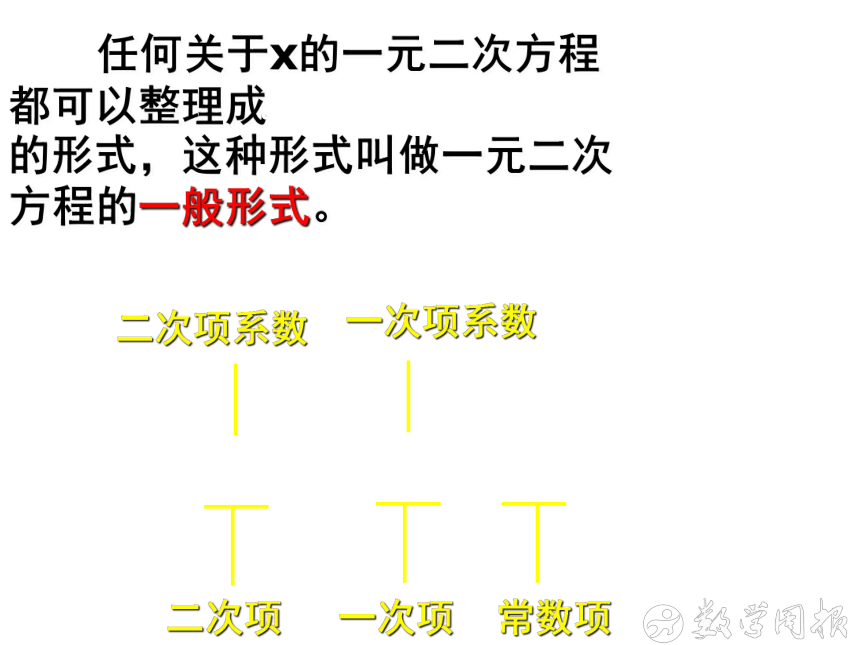
任何关于x的一元二次方程都可以整理成 的形式,这种形式叫做一元二次方程的一般形式。
二次项
一次项
常数项
二次项系数
一次项系数
例1 下列关于x的一元二次方程有 .
(2)
【例2】写出方程
的二次项系数,一次项系数及常
数项。
去括号得方程的一般形式:
二次项系数是5
一次项系数是8
常数项是-2
解:
【例3】方程
是关于
x的一元二次方程,求m的值?
要使已知方程为关于x的一元二
次方程,需满足条件:
解:
|m|+1=2
m-1≠0
m=±1
m≠1
因此 m=-1
【例4】旧车交易市场有一辆原价为12万
元的轿车,但已使用3年,如果每一 年
的折旧率为20%,以后折旧率有所变化,
现知第三年末这辆轿车价调整到7.776
万元,求这辆车第二年、第三年平均每
年的折旧率。(只列方程,不必解答)
解:
设第二年、第三年平均每年的折旧率为x,根据题意,得
小结:
(1)一元二次方程的概念;
(2)一元二次方程的一般形式,以及
系数、项的概念。
再见
(第一课时)
绿苑小区住宅设计,准备在每两幢
楼之间,开辟面积为900平方米的一块
长方形绿地,并且长比宽多10米,则绿
地的长和宽各为多少?
设宽为x,则长为(x+10)
整理可得
学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册,求这两年的平均增长率。
设这两年的平均增长率为x
今年底的图书数是5(1+x)万册
明年底的图书数是5(1+x)(1+x)万册
可列方程
只含有一个未知数,并且未知数的
最高次数是为2的整式方程叫做一元二
次方程。
(1)是整式方程;
(2)只含有一个未知数;
(3)未知数的最高次数是2。
一元一次方程:
一元二次方程:
二元一次方程:
含一个未知数,最高次数为1
含二个未知数,最高次数为1
含一个未知数,最高次数为2
任何关于x的一元二次方程都可以整理成 的形式,这种形式叫做一元二次方程的一般形式。
二次项
一次项
常数项
二次项系数
一次项系数
例1 下列关于x的一元二次方程有 .
(2)
【例2】写出方程
的二次项系数,一次项系数及常
数项。
去括号得方程的一般形式:
二次项系数是5
一次项系数是8
常数项是-2
解:
【例3】方程
是关于
x的一元二次方程,求m的值?
要使已知方程为关于x的一元二
次方程,需满足条件:
解:
|m|+1=2
m-1≠0
m=±1
m≠1
因此 m=-1
【例4】旧车交易市场有一辆原价为12万
元的轿车,但已使用3年,如果每一 年
的折旧率为20%,以后折旧率有所变化,
现知第三年末这辆轿车价调整到7.776
万元,求这辆车第二年、第三年平均每
年的折旧率。(只列方程,不必解答)
解:
设第二年、第三年平均每年的折旧率为x,根据题意,得
小结:
(1)一元二次方程的概念;
(2)一元二次方程的一般形式,以及
系数、项的概念。
再见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
