2021-2022学年度北师大版九年级数学下册课件 2.2二次函数的图象与性质(第二课时)(共26张ppt)
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学下册课件 2.2二次函数的图象与性质(第二课时)(共26张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 20:04:39 | ||
图片预览





文档简介
(共26张PPT)
北师大版九年级下册第二章《二次函数》
2.2二次函数的图象与性质(第二课时)
你能用配方的方法把y=3x2-6x+5变形成y=3(x-1)2+2的形式吗
二次函数y=ax +bx+c的图象
二次函数y=3x2-6x+5的图象是什么形状 它与我们已经作过的二次函数的图象有什么关系
想一想
驶向胜利的彼岸
在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.
由于y=3x2-6x+5=3(x-1)2+2,因此我们先作二次函数y=3(x-1)2的图象.
比较函数 与 的图象
想一想
驶向胜利的彼岸
(2)在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.
⑴完成下表,并比较3x2和3(x-1)2的值,它们之间有什么关系
x -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27 48
27 12 3 0 3 12 27 48
48 27 12 3 0 3 12 27
做一做
驶向胜利的彼岸
观察图象,回答问题
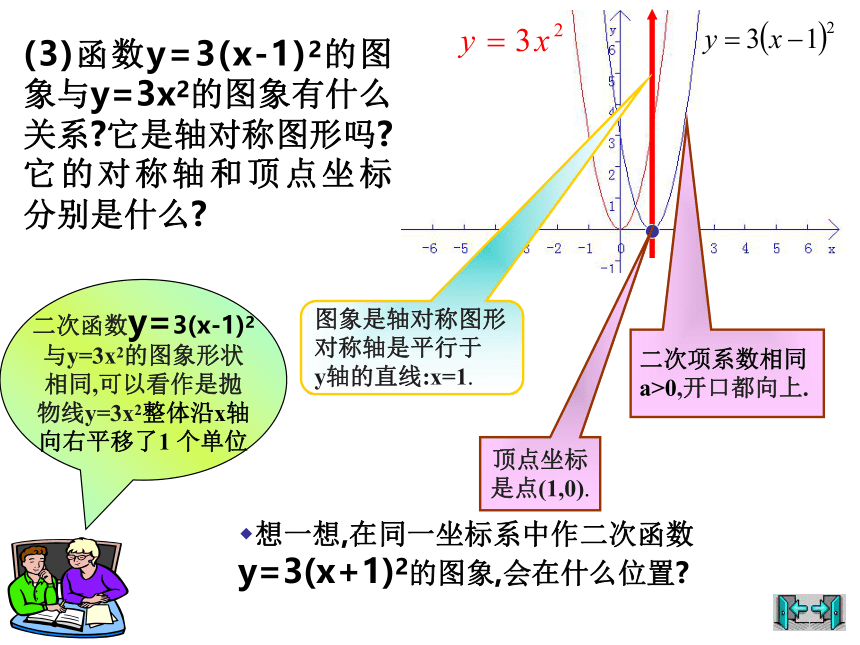
(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
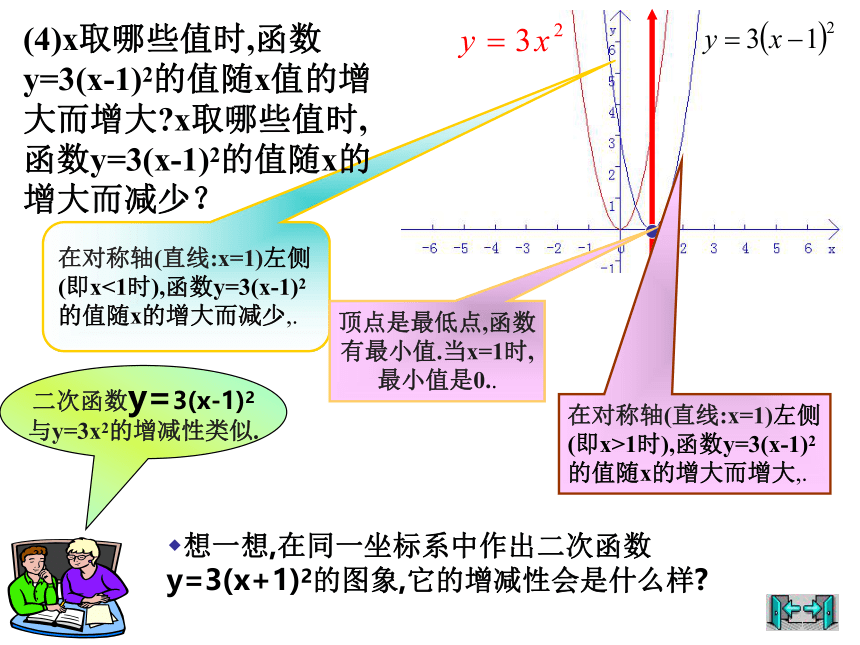
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
图象是轴对称图形
对称轴是平行于
y轴的直线:x=1.
顶点坐标
是点(1,0).
二次函数y=3(x-1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向右平移了1 个单位
(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
二次项系数相同
a>0,开口都向上.
想一想,在同一坐标系中作二次函数y=3(x+1)2的图象,会在什么位置
在对称轴(直线:x=1)左侧
(即x<1时),函数y=3(x-1)2
的值随x的增大而减少,.
顶点是最低点,函数
有最小值.当x=1时,
最小值是0..
二次函数y=3(x-1)2
与y=3x2的增减性类似.
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
在对称轴(直线:x=1)左侧
(即x>1时),函数y=3(x-1)2
的值随x的增大而增大,.
想一想,在同一坐标系中作出二次函数y=3(x+1)2的图象,它的增减性会是什么样
议一议
驶向胜利的彼岸
真知 从实践走来
1.在上面的坐标系中作出二次函数y=3(x+1)2的图象.它与二次函数y=3x2和y=3(x-1)2的图象有什么关系?它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x+1)2的图象.
做一做
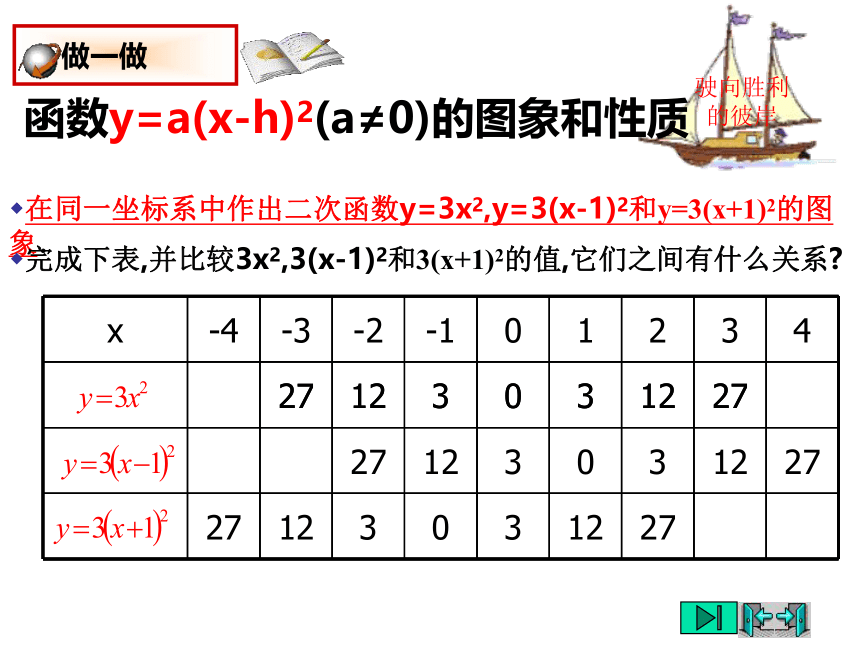
完成下表,并比较3x2,3(x-1)2和3(x+1)2的值,它们之间有什么关系
驶向胜利的彼岸
函数y=a(x-h)2(a≠0)的图象和性质
x -4 -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
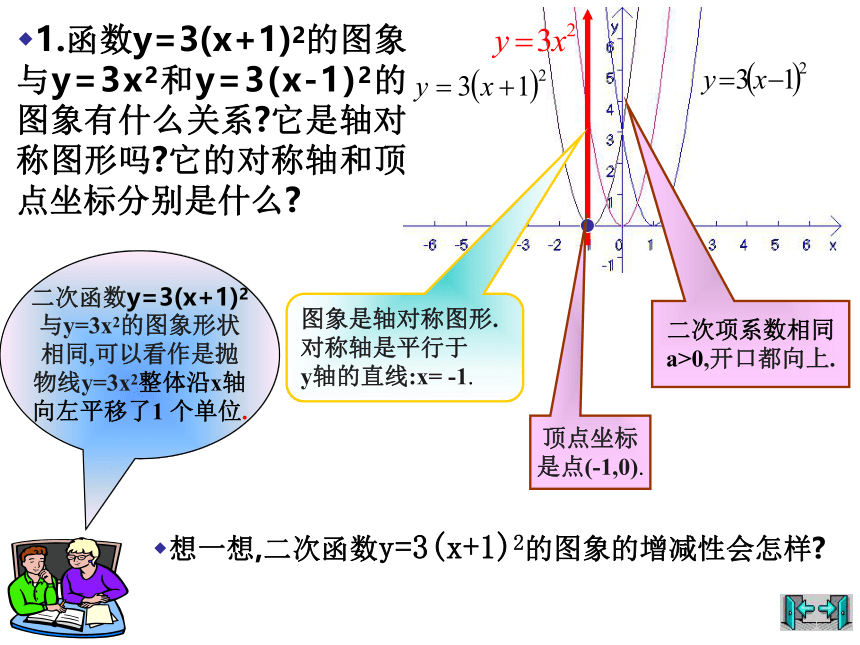
图象是轴对称图形.
对称轴是平行于
y轴的直线:x= -1.
顶点坐标
是点(-1,0).
二次函数y=3(x+1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向左平移了1 个单位.
1.函数y=3(x+1)2的图象与y=3x2和y=3(x-1)2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
二次项系数相同
a>0,开口都向上.
想一想,二次函数y=3(x+1)2的图象的增减性会怎样
在对称轴(直线:x=-1)左侧
(即x<-1时),函数y=3(x+1)2
的值随x的增大而减少,.
顶点是最低点,函数
有最小值.当x=-1时,
最小值是0..
二次函数y=3(x+1)2
与y=3x2的增减性类似.
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在对称轴(直线:x=-1)右侧
(即x>-1时),函数y=3(x+1)2
的值随x的增大而增大,.
猜一猜,函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象的位置和形状.
请你总结二次函数y=a(x-h)2的图象和性质.
2.抛物线y=-3(x-1)2和y=-3(x+1)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
y
3.抛物线y=-3(x-1)2在对称轴(x=1)的左侧,当x<1时, y随着x的增大而增大;在对称轴(x=1)右侧,当x>1时, y随着x的增大而减小.当x=1时,函数y的值最大(是0);
抛物线y=-3(x+1)2在对称轴(x=-1)的左侧,当x<-1时, y随着x的增大而增大;在对称轴(x=-1)右侧,当x>-1时, y随着x的增大而减小.当x=-1时,函数y的值最大(是0).
二次函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象
4.抛物线y=-3(x-1)2可以看作是抛物线y=-3x2沿x轴向右平移了1个单位;抛物线y=-3(x+1)2可以看作是抛物线y=-3x2沿x轴向左平移了1个单位.
X=-1
X=1
1.抛物线y=-3(x-1)2的顶点是(1,0);对称轴是直线:x=1;抛物线y=-3(x+1)2的顶点是(-1,0);对称轴是直线:x=-1.
1.抛物线y=a(x-h)2的顶点是(h,0),对称轴是平行于y轴的直线x=h.
3.当a>0时,在对称轴(x=h)的左侧,y随着x的增大而减小;在对称轴(x=h)右侧,y随着x的增大而增大;当x=h时函数y的值最小(是0).
当a<0时,在对称轴(x=h)的左侧,y随着x的增大而增大;在对称轴(x=h)的右侧,y随着x增大而减小;当x=h时,函数y的值最大(是0).
二次函数y=a(x-h)2的性质
2.当a>0时,抛物线y=a(x-h)2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=a(x-h)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
X=h
X=h
4. 越大,开口越小,
越小,开口越大.
二次函数y=a(x-h)2
与y=ax2的图象形状
相同,可以看作是抛
物线y=ax2整体沿x轴
平移了 个单位(当h>0时,向右移 个单位;当h<0时,向左移 个单位)得到的.
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
开口大小
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2 (a>0)
y=a(x-h)2 (a<0)
(h,0)
(h,0)
直线x=h
直线x=h
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=h时,最小值为0.
当x=h时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
越小,开口越大.
越大,开口越小.
我思,我进步
在同一坐标系中作出二次函数y=3x ,y=3(x-1)2和y=3(x-1)2+2的图象.
做一做
驶向胜利的彼岸
二次函数y=3x ,y=3(x-1)2和y=3(x-1)2+2的图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么 作图看一看.
在同一坐标系中作出函数y=3x ,y=3(x-1)2和y=3(x-1)2+2的图象.
做一做
完成下表,并比较3x2,3(x-1)2和3(x-1)2+2值,它们之间有何关系
驶向胜利的彼岸
函数y=a(x-h)2+k(a≠0)的图象和性质
x -4 -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
29 14 5 2 5 14 29
对称轴仍是平行于y轴的直
线(x=1);增减性与y=3x2类似.
顶点是(1,2).
二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.
二次函数y=3(x-1)2+2的图象和抛物线y=3x ,y=3(x-1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向上,当
X=1时有最小
值:且最小值=2.
先猜一猜,再做一做,在同一坐标系中作二次函数y=3(x-1)2-2,会是什么样
X=1
对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似.
顶点是(1,-2).
二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.
二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系 它的开口方向、对称轴和顶点坐标分别是什么
开口向上,
当x=1时y有
最小值:且
最小值= -2.
想一想,二次函数y=-3(x-1)2+2和y=-3x ,y=-3(x-1)2的图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么 再作图看一看.
X=1
我思,我进步
在同一坐标系中作出二次函数y=-3(x-1)2+2,y=-3(x-1)2-2,y=-3x 和y=-3(x-1)2的图象
议一义
驶向胜利的彼岸
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x ,y=-3(x-1)2的图象有什么关系 它们是轴对称图形吗 它的开口方向、对称轴和顶点坐标分别是什么 当x取哪些值时,y的值随x值的增大而增大 当x取哪些值时,y的值随x值的增大而减小
对称轴仍是平行于y轴的直线
(x=1);增减性与y= -3x2类似.
顶点分别是
(1,2)和(1,-2).
二次函数y=-3(x-1)2+2与
y=-3(x-1)2+2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x ,y=-3(x-1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向下,
当x=1时y有
最大值:且
最大值= 2
(或最大值=-2).
想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x ,y=-3(x+1)2
y
X=1
对称轴仍是平行于y轴的直线
(x=-1);增减性与y= -3x2类似.
顶点分别是
(-1,2)和(-1,-2)..
二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x ,y=-3(x-1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向下,
当x=-1时y有
最大值:且
最大值= 2
(或最大值=-2).
先想一想,再总结二次函数y=a(x-h)2+k的图象和性质.
X=1
二次函数y=a(x-h) +k与=ax 的关系
一般地,由y=ax 的图象便可得到二次函数y=a(x-h) +k的图象:y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h) +k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关.
二次函数y=a(x+h)2+k的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(-h,k)
(-h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
悟出真谛,练出本事
1.指出下列函数图象的开口方向对称轴和顶点坐标:
2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
(2)二次函数y=-3(x-2)2+4的图象与二次函数y=-3x2的图象有什么关系
对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大 当x取哪些值时,y的值随x值的增大而减小 二次函数y=3(x+1)2+4呢
随堂练习
驶向胜利的彼岸
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
2.不同点: 只是位置不同(1)顶点不同:分别是(-h,k)和(0,0).
(2)对称轴不同:分别是直线x= -h和y轴.
(2)最值不同:分别是k和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
驶向胜利的彼岸
小结 拓展
回味无穷
二次函数y=a(x-h) +k与=ax 的关系
独立
作业
1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.
2.填写下表:
y=a(x-h) +k 开口方向 对称轴 顶点坐标
a>0
a<0
北师大版九年级下册第二章《二次函数》
2.2二次函数的图象与性质(第二课时)
你能用配方的方法把y=3x2-6x+5变形成y=3(x-1)2+2的形式吗
二次函数y=ax +bx+c的图象
二次函数y=3x2-6x+5的图象是什么形状 它与我们已经作过的二次函数的图象有什么关系
想一想
驶向胜利的彼岸
在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.
由于y=3x2-6x+5=3(x-1)2+2,因此我们先作二次函数y=3(x-1)2的图象.
比较函数 与 的图象
想一想
驶向胜利的彼岸
(2)在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.
⑴完成下表,并比较3x2和3(x-1)2的值,它们之间有什么关系
x -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27 48
27 12 3 0 3 12 27 48
48 27 12 3 0 3 12 27
做一做
驶向胜利的彼岸
观察图象,回答问题
(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
图象是轴对称图形
对称轴是平行于
y轴的直线:x=1.
顶点坐标
是点(1,0).
二次函数y=3(x-1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向右平移了1 个单位
(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
二次项系数相同
a>0,开口都向上.
想一想,在同一坐标系中作二次函数y=3(x+1)2的图象,会在什么位置
在对称轴(直线:x=1)左侧
(即x<1时),函数y=3(x-1)2
的值随x的增大而减少,.
顶点是最低点,函数
有最小值.当x=1时,
最小值是0..
二次函数y=3(x-1)2
与y=3x2的增减性类似.
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
在对称轴(直线:x=1)左侧
(即x>1时),函数y=3(x-1)2
的值随x的增大而增大,.
想一想,在同一坐标系中作出二次函数y=3(x+1)2的图象,它的增减性会是什么样
议一议
驶向胜利的彼岸
真知 从实践走来
1.在上面的坐标系中作出二次函数y=3(x+1)2的图象.它与二次函数y=3x2和y=3(x-1)2的图象有什么关系?它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x+1)2的图象.
做一做
完成下表,并比较3x2,3(x-1)2和3(x+1)2的值,它们之间有什么关系
驶向胜利的彼岸
函数y=a(x-h)2(a≠0)的图象和性质
x -4 -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
图象是轴对称图形.
对称轴是平行于
y轴的直线:x= -1.
顶点坐标
是点(-1,0).
二次函数y=3(x+1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向左平移了1 个单位.
1.函数y=3(x+1)2的图象与y=3x2和y=3(x-1)2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
二次项系数相同
a>0,开口都向上.
想一想,二次函数y=3(x+1)2的图象的增减性会怎样
在对称轴(直线:x=-1)左侧
(即x<-1时),函数y=3(x+1)2
的值随x的增大而减少,.
顶点是最低点,函数
有最小值.当x=-1时,
最小值是0..
二次函数y=3(x+1)2
与y=3x2的增减性类似.
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大 x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在对称轴(直线:x=-1)右侧
(即x>-1时),函数y=3(x+1)2
的值随x的增大而增大,.
猜一猜,函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象的位置和形状.
请你总结二次函数y=a(x-h)2的图象和性质.
2.抛物线y=-3(x-1)2和y=-3(x+1)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
y
3.抛物线y=-3(x-1)2在对称轴(x=1)的左侧,当x<1时, y随着x的增大而增大;在对称轴(x=1)右侧,当x>1时, y随着x的增大而减小.当x=1时,函数y的值最大(是0);
抛物线y=-3(x+1)2在对称轴(x=-1)的左侧,当x<-1时, y随着x的增大而增大;在对称轴(x=-1)右侧,当x>-1时, y随着x的增大而减小.当x=-1时,函数y的值最大(是0).
二次函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象
4.抛物线y=-3(x-1)2可以看作是抛物线y=-3x2沿x轴向右平移了1个单位;抛物线y=-3(x+1)2可以看作是抛物线y=-3x2沿x轴向左平移了1个单位.
X=-1
X=1
1.抛物线y=-3(x-1)2的顶点是(1,0);对称轴是直线:x=1;抛物线y=-3(x+1)2的顶点是(-1,0);对称轴是直线:x=-1.
1.抛物线y=a(x-h)2的顶点是(h,0),对称轴是平行于y轴的直线x=h.
3.当a>0时,在对称轴(x=h)的左侧,y随着x的增大而减小;在对称轴(x=h)右侧,y随着x的增大而增大;当x=h时函数y的值最小(是0).
当a<0时,在对称轴(x=h)的左侧,y随着x的增大而增大;在对称轴(x=h)的右侧,y随着x增大而减小;当x=h时,函数y的值最大(是0).
二次函数y=a(x-h)2的性质
2.当a>0时,抛物线y=a(x-h)2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=a(x-h)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
X=h
X=h
4. 越大,开口越小,
越小,开口越大.
二次函数y=a(x-h)2
与y=ax2的图象形状
相同,可以看作是抛
物线y=ax2整体沿x轴
平移了 个单位(当h>0时,向右移 个单位;当h<0时,向左移 个单位)得到的.
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
开口大小
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2 (a>0)
y=a(x-h)2 (a<0)
(h,0)
(h,0)
直线x=h
直线x=h
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=h时,最小值为0.
当x=h时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
越小,开口越大.
越大,开口越小.
我思,我进步
在同一坐标系中作出二次函数y=3x ,y=3(x-1)2和y=3(x-1)2+2的图象.
做一做
驶向胜利的彼岸
二次函数y=3x ,y=3(x-1)2和y=3(x-1)2+2的图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么 作图看一看.
在同一坐标系中作出函数y=3x ,y=3(x-1)2和y=3(x-1)2+2的图象.
做一做
完成下表,并比较3x2,3(x-1)2和3(x-1)2+2值,它们之间有何关系
驶向胜利的彼岸
函数y=a(x-h)2+k(a≠0)的图象和性质
x -4 -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
29 14 5 2 5 14 29
对称轴仍是平行于y轴的直
线(x=1);增减性与y=3x2类似.
顶点是(1,2).
二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.
二次函数y=3(x-1)2+2的图象和抛物线y=3x ,y=3(x-1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向上,当
X=1时有最小
值:且最小值=2.
先猜一猜,再做一做,在同一坐标系中作二次函数y=3(x-1)2-2,会是什么样
X=1
对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似.
顶点是(1,-2).
二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.
二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系 它的开口方向、对称轴和顶点坐标分别是什么
开口向上,
当x=1时y有
最小值:且
最小值= -2.
想一想,二次函数y=-3(x-1)2+2和y=-3x ,y=-3(x-1)2的图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么 再作图看一看.
X=1
我思,我进步
在同一坐标系中作出二次函数y=-3(x-1)2+2,y=-3(x-1)2-2,y=-3x 和y=-3(x-1)2的图象
议一义
驶向胜利的彼岸
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x ,y=-3(x-1)2的图象有什么关系 它们是轴对称图形吗 它的开口方向、对称轴和顶点坐标分别是什么 当x取哪些值时,y的值随x值的增大而增大 当x取哪些值时,y的值随x值的增大而减小
对称轴仍是平行于y轴的直线
(x=1);增减性与y= -3x2类似.
顶点分别是
(1,2)和(1,-2).
二次函数y=-3(x-1)2+2与
y=-3(x-1)2+2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x ,y=-3(x-1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向下,
当x=1时y有
最大值:且
最大值= 2
(或最大值=-2).
想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x ,y=-3(x+1)2
y
X=1
对称轴仍是平行于y轴的直线
(x=-1);增减性与y= -3x2类似.
顶点分别是
(-1,2)和(-1,-2)..
二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x ,y=-3(x-1)2有什么关系 它的开口方向,对称轴和顶点坐标分别是什么
开口向下,
当x=-1时y有
最大值:且
最大值= 2
(或最大值=-2).
先想一想,再总结二次函数y=a(x-h)2+k的图象和性质.
X=1
二次函数y=a(x-h) +k与=ax 的关系
一般地,由y=ax 的图象便可得到二次函数y=a(x-h) +k的图象:y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h) +k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关.
二次函数y=a(x+h)2+k的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(-h,k)
(-h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
悟出真谛,练出本事
1.指出下列函数图象的开口方向对称轴和顶点坐标:
2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什么关系 它是轴对称图形吗 它的对称轴和顶点坐标分别是什么
(2)二次函数y=-3(x-2)2+4的图象与二次函数y=-3x2的图象有什么关系
对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大 当x取哪些值时,y的值随x值的增大而减小 二次函数y=3(x+1)2+4呢
随堂练习
驶向胜利的彼岸
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
2.不同点: 只是位置不同(1)顶点不同:分别是(-h,k)和(0,0).
(2)对称轴不同:分别是直线x= -h和y轴.
(2)最值不同:分别是k和0.
3.联系: y=a(x-h) +k(a≠0) 的图象可以看成y=ax 的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
驶向胜利的彼岸
小结 拓展
回味无穷
二次函数y=a(x-h) +k与=ax 的关系
独立
作业
1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.
2.填写下表:
y=a(x-h) +k 开口方向 对称轴 顶点坐标
a>0
a<0
