2021-2022学年度北师大版九年级数学下册课件 3.2圆的对称性(第1课时)(共13张ppt)
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学下册课件 3.2圆的对称性(第1课时)(共13张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 581.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 21:17:04 | ||
图片预览

文档简介
(共13张PPT)
北师大版九年级下册第三章《圆》
3.2圆的对称性
(第1课时)
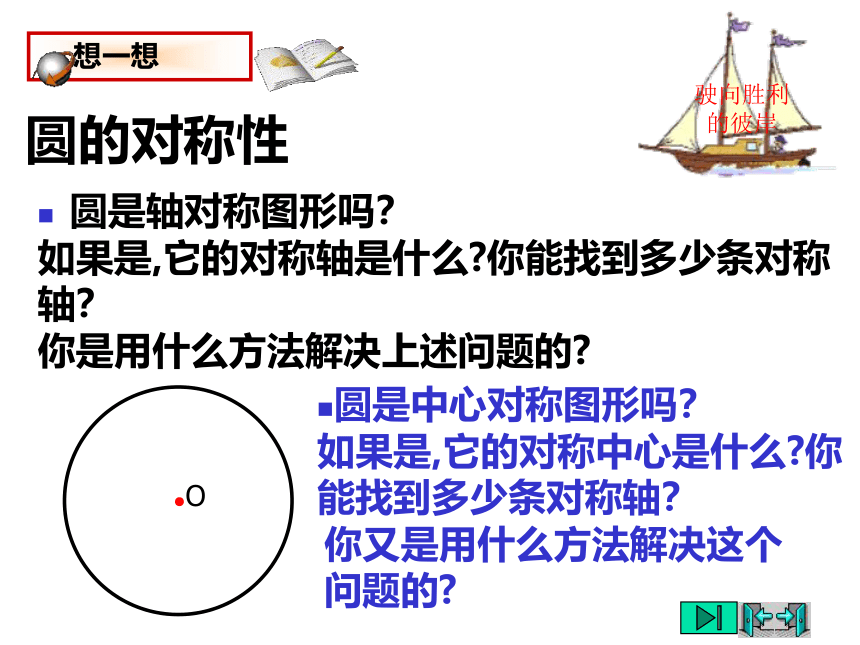
圆的对称性
圆是轴对称图形吗?
想一想
驶向胜利的彼岸
如果是,它的对称轴是什么 你能找到多少条对称轴?
●O
你是用什么方法解决上述问题的
圆是中心对称图形吗?
如果是,它的对称中心是什么 你能找到多少条对称轴?
你又是用什么方法解决这个问题的
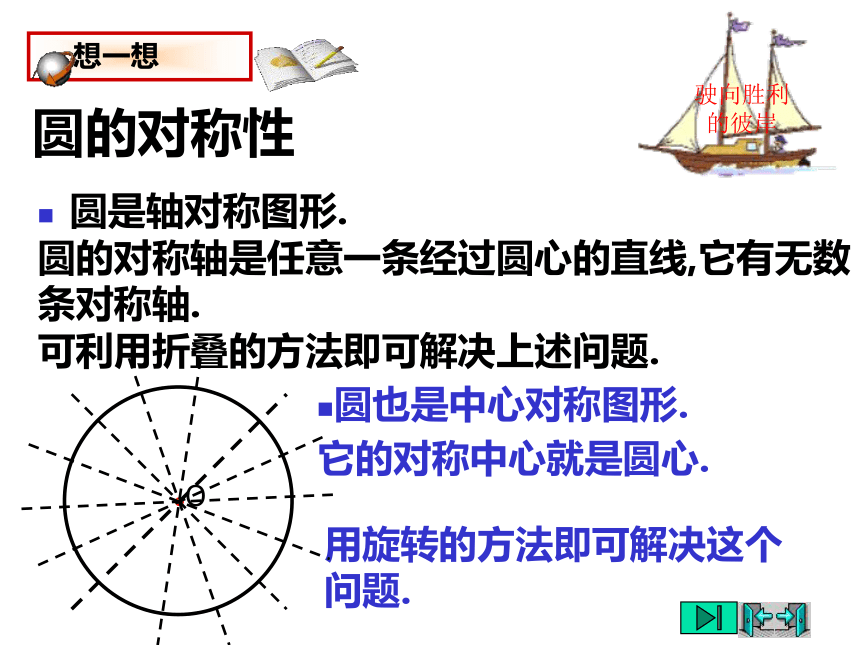
圆的对称性
圆是轴对称图形.
想一想
驶向胜利的彼岸
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可解决这个问题.
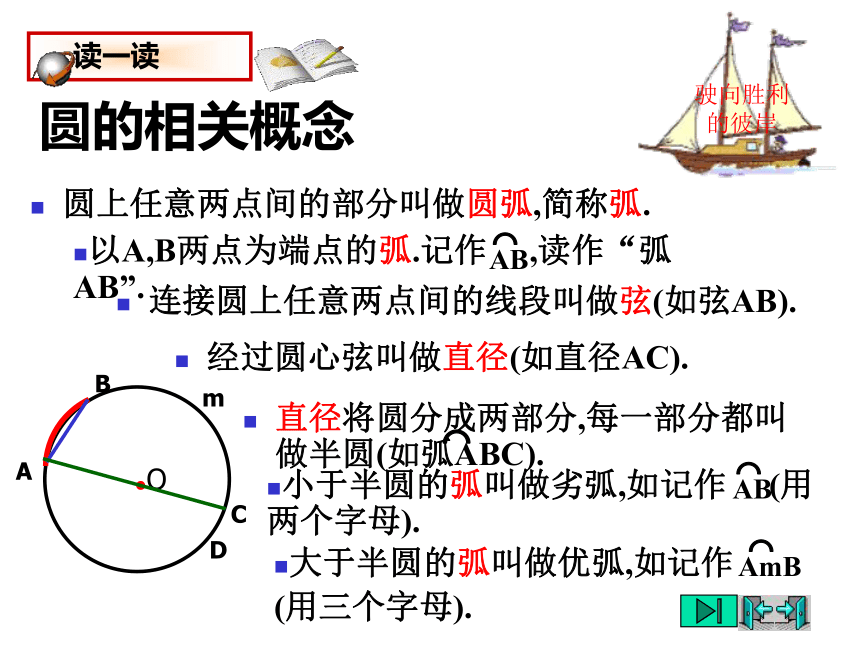
圆的相关概念
圆上任意两点间的部分叫做圆弧,简称弧.
直径将圆分成两部分,每一部分都叫做半圆(如弧ABC).
读一读
驶向胜利的彼岸
连接圆上任意两点间的线段叫做弦(如弦AB).
●O
经过圆心弦叫做直径(如直径AC).
AB
⌒
以A,B两点为端点的弧.记作 ,读作“弧AB”.
AB
⌒
小于半圆的弧叫做劣弧,如记作 (用两个字母).
⌒
AmB
大于半圆的弧叫做优弧,如记作
(用三个字母).
A
B
C
⌒
m
D
③AM=BM,
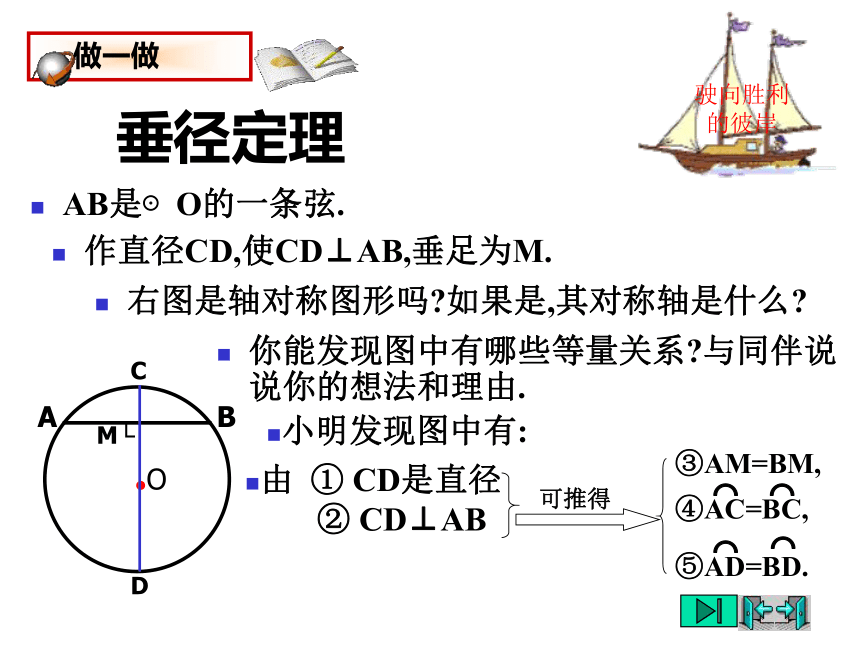
垂径定理
AB是⊙O的一条弦.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
做一做
驶向胜利的彼岸
作直径CD,使CD⊥AB,垂足为M.
●O
右图是轴对称图形吗 如果是,其对称轴是什么
小明发现图中有:
A
B
C
D
M└
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理
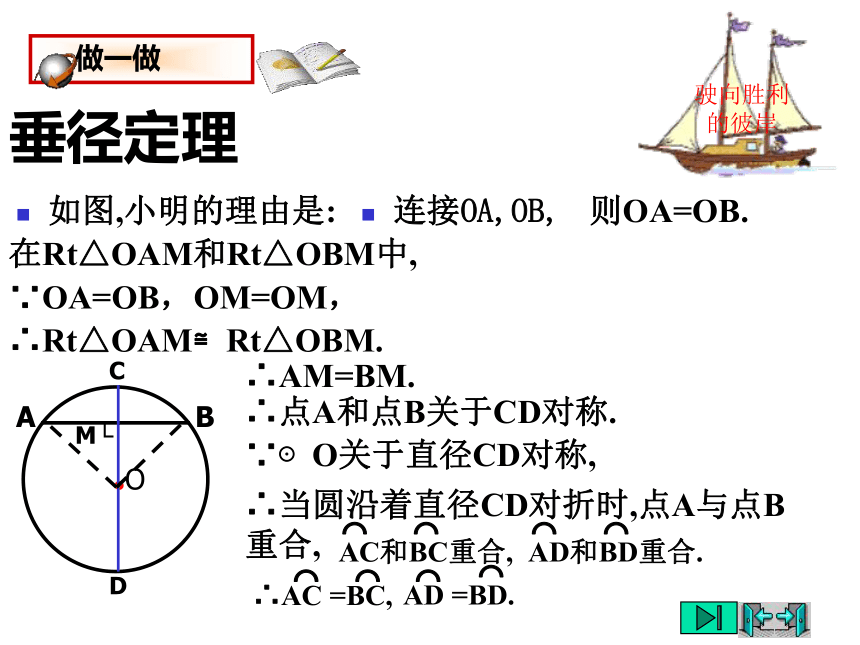
如图,小明的理由是:
连接OA,OB,
做一做
驶向胜利的彼岸
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
垂径定理三种语言
定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
老师提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
想一想
驶向胜利的彼岸
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
②CD⊥AB,
垂径定理的逆定理
AB是⊙O的一条弦,且AM=BM.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
做一做
驶向胜利的彼岸
过点M作直径CD.
●O
右图是轴对称图形吗 如果是,其对称轴是什么
小明发现图中有:
C
D
由 ① CD是直径
③ AM=BM
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
●
M
A
B
┗
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
你可以写出相应的命题吗
相信自己是最棒的!
垂径定理的逆定理
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
想一想
驶向胜利的彼岸
●O
A
B
C
D
M└
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理及逆定理
想一想
驶向胜利的彼岸
条件 结论 命题
①② ③④⑤
①③ ②④⑤
①④ ②③⑤
①⑤ ②③④
②③ ①④⑤
②④ ①③⑤
②⑤ ①③④
③④ ①②⑤
③⑤ ①②④
④⑤ ①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
试一试
驶向胜利的彼岸
挑战自我画一画
1、如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
试一试
驶向胜利的彼岸
挑战自我填一填
2、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦. ( )
⑷弦的垂直平分线一定平分这条弦所对的弧. ( )
北师大版九年级下册第三章《圆》
3.2圆的对称性
(第1课时)
圆的对称性
圆是轴对称图形吗?
想一想
驶向胜利的彼岸
如果是,它的对称轴是什么 你能找到多少条对称轴?
●O
你是用什么方法解决上述问题的
圆是中心对称图形吗?
如果是,它的对称中心是什么 你能找到多少条对称轴?
你又是用什么方法解决这个问题的
圆的对称性
圆是轴对称图形.
想一想
驶向胜利的彼岸
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可解决这个问题.
圆的相关概念
圆上任意两点间的部分叫做圆弧,简称弧.
直径将圆分成两部分,每一部分都叫做半圆(如弧ABC).
读一读
驶向胜利的彼岸
连接圆上任意两点间的线段叫做弦(如弦AB).
●O
经过圆心弦叫做直径(如直径AC).
AB
⌒
以A,B两点为端点的弧.记作 ,读作“弧AB”.
AB
⌒
小于半圆的弧叫做劣弧,如记作 (用两个字母).
⌒
AmB
大于半圆的弧叫做优弧,如记作
(用三个字母).
A
B
C
⌒
m
D
③AM=BM,
垂径定理
AB是⊙O的一条弦.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
做一做
驶向胜利的彼岸
作直径CD,使CD⊥AB,垂足为M.
●O
右图是轴对称图形吗 如果是,其对称轴是什么
小明发现图中有:
A
B
C
D
M└
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理
如图,小明的理由是:
连接OA,OB,
做一做
驶向胜利的彼岸
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
垂径定理三种语言
定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.
老师提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
想一想
驶向胜利的彼岸
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
②CD⊥AB,
垂径定理的逆定理
AB是⊙O的一条弦,且AM=BM.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
做一做
驶向胜利的彼岸
过点M作直径CD.
●O
右图是轴对称图形吗 如果是,其对称轴是什么
小明发现图中有:
C
D
由 ① CD是直径
③ AM=BM
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
●
M
A
B
┗
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
你可以写出相应的命题吗
相信自己是最棒的!
垂径定理的逆定理
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
想一想
驶向胜利的彼岸
●O
A
B
C
D
M└
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理及逆定理
想一想
驶向胜利的彼岸
条件 结论 命题
①② ③④⑤
①③ ②④⑤
①④ ②③⑤
①⑤ ②③④
②③ ①④⑤
②④ ①③⑤
②⑤ ①③④
③④ ①②⑤
③⑤ ①②④
④⑤ ①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
试一试
驶向胜利的彼岸
挑战自我画一画
1、如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
试一试
驶向胜利的彼岸
挑战自我填一填
2、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦. ( )
⑷弦的垂直平分线一定平分这条弦所对的弧. ( )
