2021-2022学年度北师大版九年级数学下册课件 3.3垂径定理(共12张ppt)
文档属性
| 名称 | 2021-2022学年度北师大版九年级数学下册课件 3.3垂径定理(共12张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 21:21:35 | ||
图片预览



文档简介
(共12张PPT)
北师大版九年级下册第三章《圆》
3.3垂径定理
问题:左图中AB为圆O的直径,CD为圆O的弦。相交于点E,当弦CD在圆上运动的过程中有没有特殊情况?
运动CD
直径AB和弦CD互相垂直
特殊情况
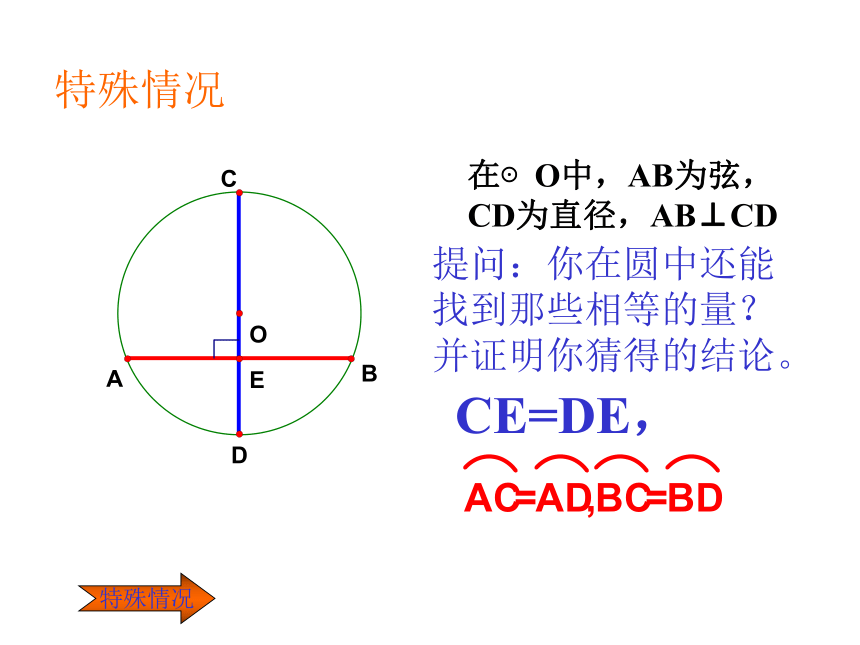
在⊙O中,AB为弦,CD为直径,AB⊥CD
提问:你在圆中还能找到那些相等的量?并证明你猜得的结论。
特殊情况
CE=DE,
证明结论
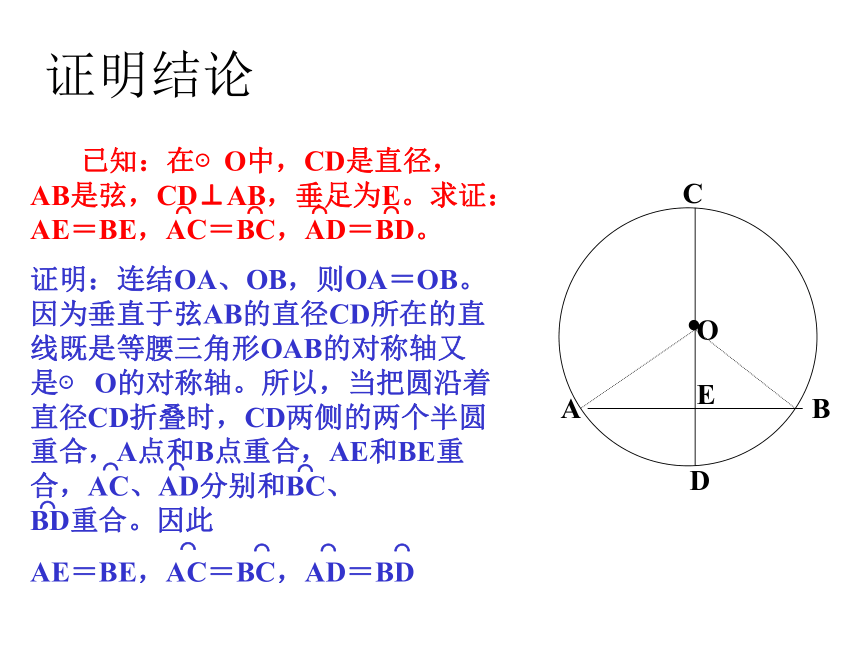
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。求证:AE=BE,AC=BC,AD=BD。
⌒
⌒
⌒
⌒
证明:连结OA、OB,则OA=OB。因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙ O的对称轴。所以,当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AE和BE重合,AC、AD分别和BC、 BD重合。因此
AE=BE,AC=BC,AD=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
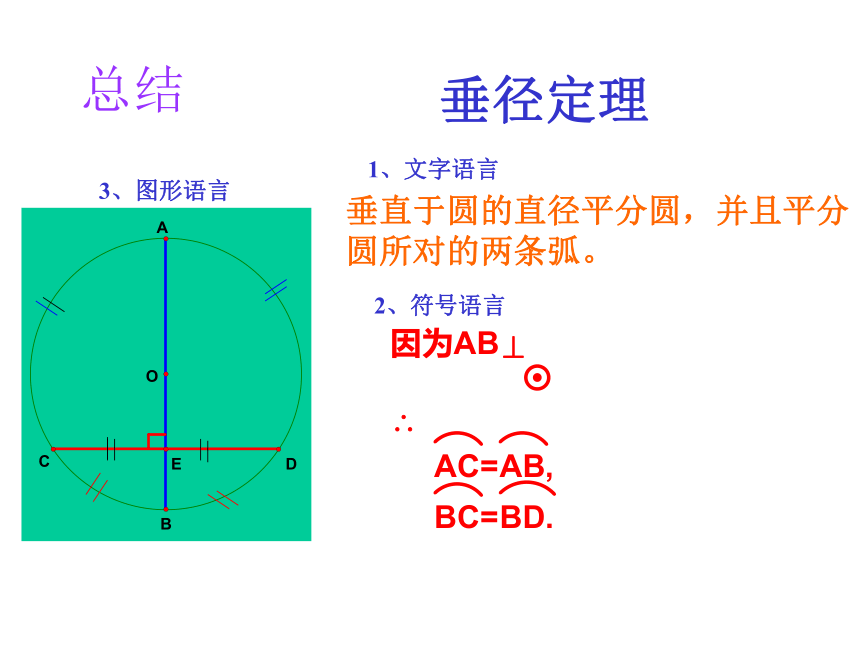
垂径定理
垂直于圆的直径平分圆,并且平分 圆所对的两条弧。
总结
1、文字语言
2、符号语言
3、图形语言
2、请画图说明垂径定理的条件和结论。
1、判断下列图是否是表示垂径定理的图形。
是
不是
是
条件
结论
(1)过圆心
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
分析
CD为直径,
CD⊥AB
}
{
点C平分弧
ACB
点D平分弧
ADB
例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。
则OE=3厘米,AE=BE。∵AB=8厘米 ∴AE=4厘米
在Rt△AOE中,根据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米。
.
A
E
B
O
例题1
解:连结OA。过O作OE⊥AB,垂足为E,
例2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BD
E
.
A
C
D
B
O
例题2
证明:过O作OE⊥AB,垂足为E,
┐
例3 已知:⊙O中弦AB∥CD。
求证:AC=BD
⌒
⌒
∵AB∥CD,∴MN⊥CD。则AM=BM,CM=DM(垂直平分弦的直径平分弦所对的弦)
AM-CM=BM-DM
∴AC=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
.
M
C
D
A
B
O
N
例题3
证明:作直径MN⊥AB。
北师大版九年级下册第三章《圆》
3.3垂径定理
问题:左图中AB为圆O的直径,CD为圆O的弦。相交于点E,当弦CD在圆上运动的过程中有没有特殊情况?
运动CD
直径AB和弦CD互相垂直
特殊情况
在⊙O中,AB为弦,CD为直径,AB⊥CD
提问:你在圆中还能找到那些相等的量?并证明你猜得的结论。
特殊情况
CE=DE,
证明结论
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。求证:AE=BE,AC=BC,AD=BD。
⌒
⌒
⌒
⌒
证明:连结OA、OB,则OA=OB。因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙ O的对称轴。所以,当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AE和BE重合,AC、AD分别和BC、 BD重合。因此
AE=BE,AC=BC,AD=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
C
.
O
A
E
B
D
垂径定理
垂直于圆的直径平分圆,并且平分 圆所对的两条弧。
总结
1、文字语言
2、符号语言
3、图形语言
2、请画图说明垂径定理的条件和结论。
1、判断下列图是否是表示垂径定理的图形。
是
不是
是
条件
结论
(1)过圆心
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
分析
CD为直径,
CD⊥AB
}
{
点C平分弧
ACB
点D平分弧
ADB
例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。
则OE=3厘米,AE=BE。∵AB=8厘米 ∴AE=4厘米
在Rt△AOE中,根据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米。
.
A
E
B
O
例题1
解:连结OA。过O作OE⊥AB,垂足为E,
例2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。
则AE=BE,CE=DE。
AE-CE=BE-DE。
所以,AC=BD
E
.
A
C
D
B
O
例题2
证明:过O作OE⊥AB,垂足为E,
┐
例3 已知:⊙O中弦AB∥CD。
求证:AC=BD
⌒
⌒
∵AB∥CD,∴MN⊥CD。则AM=BM,CM=DM(垂直平分弦的直径平分弦所对的弦)
AM-CM=BM-DM
∴AC=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
.
M
C
D
A
B
O
N
例题3
证明:作直径MN⊥AB。
